离散型概率分布 vs. 连续型概率分布

第一部分：核心概念与原理讲解

离散型数据

连续型数据

概率分布描述了随机变量取各个可能值的概率的规律。

离散型概率分布

连续型概率分布

描述对象：连续型随机变量的概率分布。
关键区别 ：连续型随机变量取任何一个特定值 的概率无限接近于0 （因为可能的值有无限多个）。因此，我们关心的是它在某个区间内 取值的概率。
描述方式 ：概率密度函数 。它是一条连续的曲线，函数值本身不是概率 ，而是"密度"。曲线下的面积 才代表概率。------f(x)越大，只是说明该点附近概率更集中，但具体概率要看区间。
核心性质：
1. 概率密度函数曲线始终在x轴上方，即 f(x) ≥ 0
2. 整个曲线下的总面积等于 1
概率计算 ：随机变量X在区间 [a, b] 取值的概率 P(a ≤ X ≤ b) 等于概率密度函数曲线下从a到b的面积。这个面积需要通过积分来计算。P(a ≤ X ≤ b) = ∫(a到b) f(x) dx
表示方法：用函数公式和曲线图表示。

应用场景 ：进行n次独立的重复试验（伯努利试验），每次试验只有两种可能结果（成功/失败），且每次成功的概率p相同。求成功次数X的概率分布。
概率质量函数 ：P(X=k) = C(n,k) * p^k * (1-p)^(n-k)
- C(n,k) 是组合数，计算从n次中选出k次成功的组合方式。
- k 是成功的次数 (k = 0, 1, 2, ..., n)
案例计算：一个硬币抛掷5次（n=5），正面朝上的概率p=0.5。求恰好有3次正面朝上的概率。
- P(X=3) = C(5,3) * (0.5)^3 * (0.5)^2
- C(5,3) = 10
- P(X=3) = 10 * 0.125 * 0.25 = 0.3125
- 所以，恰好3次正面朝上的概率是31.25%。

应用场景 ：描述在固定时间或空间区间内 ，稀有事件发生的次数。例如，一天内网站的访问次数、一小时内接到客服电话的次数、一平方米内玻璃瓶的气泡数。
概率质量函数 ：P(X=k) = (λ^k * e^(-λ)) / k!
- λ 是单位时间（或单位空间）内事件发生的平均次数。
- k 是事件发生的次数 (k = 0, 1, 2, ...)
- e 是自然常数 (~2.71828)
案例计算：一个便利店平均每小时有10位顾客光临（λ=10）。求下一小时恰好有7位顾客光临的概率。
- P(X=7) = (10^7 * e^(-10)) / 7!
- 7! = 5040
- e^(-10) ≈ 0.0000454
- P(X=7) ≈ (10,000,000 * 0.0000454) / 5040 ≈ 45400 / 5040 ≈ 0.090
- 所以，恰好有7位顾客的概率大约是9%。

**定义：**最常见的连续分布，呈钟形对称曲线。
应用场景 ：最重要的连续分布，俗称"钟形曲线"。自然界和社会中大量现象都近似服从正态分布。如测量误差、人群的身高体重、考试成绩等。
概率密度函数 ：
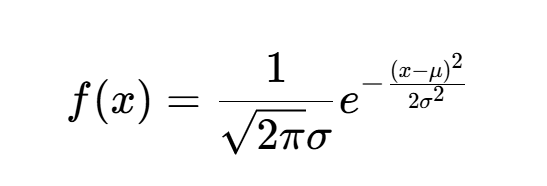
- μ 是均值，决定曲线的中心位置。
- σ 是标准差，决定曲线的"胖瘦"（分散程度）。
**特点：**68%的数据落在 μ±σ，95%落在 μ±2σ。
案例计算：假设成年男性身高服从正态分布，均值μ=175cm，标准差σ=10cm。求随机抽取一名男性，其身高在165cm到185cm之间的概率。
- 思路：计算概率密度函数曲线下从165到185的面积。直接积分非常复杂，通常将其转化为标准正态分布（μ=0, σ=1），然后查表。
1. 标准化 ：将一般正态分布转换为标准正态分布 Z = (X - μ) / σ
  - 对于165: Z1 = (165-175)/10 = -1
  - 对于185: Z2 = (185-175)/10 = 1
2. 问题转化：求 P(165 < X < 185) 等价于求 P(-1 < Z < 1)
3. 查标准正态分布表：
  - P(Z < 1) ≈ 0.8413
  - P(Z < -1) ≈ 0.1587
  - P(-1 < Z < 1) = P(Z < 1) - P(Z < -1) = 0.8413 - 0.1587 = 0.6826
- 所以，身高在165cm到185cm之间的概率约为68.26%。这正好符合正态分布的"68-95-99.7"法则（均值±1个标准差内的概率约为68%）。

**定义：**随机变量在区间 [a,b]内等可能取值。
应用场景 ：随机变量在区间 [a, b] 内取任何值的可能性完全相同 。
概率密度函数 ：
特点： 矩形形状，高度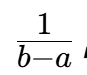，保证总面积为1。
案例计算：等公交车，公交车每10分钟一班（即等待时间X在 [0, 10] 区间上均匀分布）。求乘客等待时间少于3分钟的概率。
- 概率密度函数的高度为 1/(10-0) = 0.1
- P(0 < X < 3) = 区间 [0,3] 下方的面积 = 长 * 高 = (3 - 0) * 0.1 = 0.3
- 所以，等待时间少于3分钟的概率是30%。

分布类型	具体分布	典型应用场景
离散型	二项分布	质量检测（合格/不合格）、市场调研（购买/不购买）、医学（有效/无效）等重复次数固定的二元结果事件。
离散型	泊松分布	计数数据，特别是稀有事件：单位时间内的客服电话数、交通事故数、系统故障数、到达排队系统的人数等。
离散型	几何分布	取得第一次成功所需要的试验次数。
连续型	正态分布	自然界和社会科学中最广泛：测量误差、生理指标（身高、血压）、考试成绩、金融产品的收益率等。
连续型	均匀分布	随机模拟（生成随机数）、等概率事件（摇奖、抽签）。
连续型	指数分布	描述泊松过程中事件发生的时间间隔，如设备的寿命、客服电话的间隔时间、网页请求的到达间隔。
连续型	t分布, F分布, χ²分布	主要用于统计推断，如假设检验、方差分析、构建置信区间等。