文章目录
- 介绍
- [C 代码实现](#C 代码实现)
-
- [Hash 函数是 MurmurHash3-128bit](#Hash 函数是 MurmurHash3-128bit)
- 初始化布隆过滤器
- 销毁布隆过滤器
- 记录数据(记录存在与否而非数据本身)
- 布隆过滤器判断数据是否存在(必须把数据全部插入到位映射数组后才执行)
- 根据概率模型计算假阳率
- 测试代码(主函数)
推荐一个零声教育学习教程,个人觉得老师讲得不错,分享给大家:[Linux,Nginx,ZeroMQ,MySQL,Redis,fastdfs,MongoDB,ZK,流媒体,CDN,P2P,K8S,Docker,TCP/IP,协程,DPDK等技术内容,点击立即学习: https://github.com/0voice 链接。
介绍
布隆过滤器(Bloom Filter)是一种空间效率极高的概率型数据结构,主要用于快速判断某个元素是否"绝对不存在"于一个大型集合中。它的核心价值在于用极小的空间开销换取超高的查询速度,但需要容忍一定的误判率(假阳性)。
核心原理
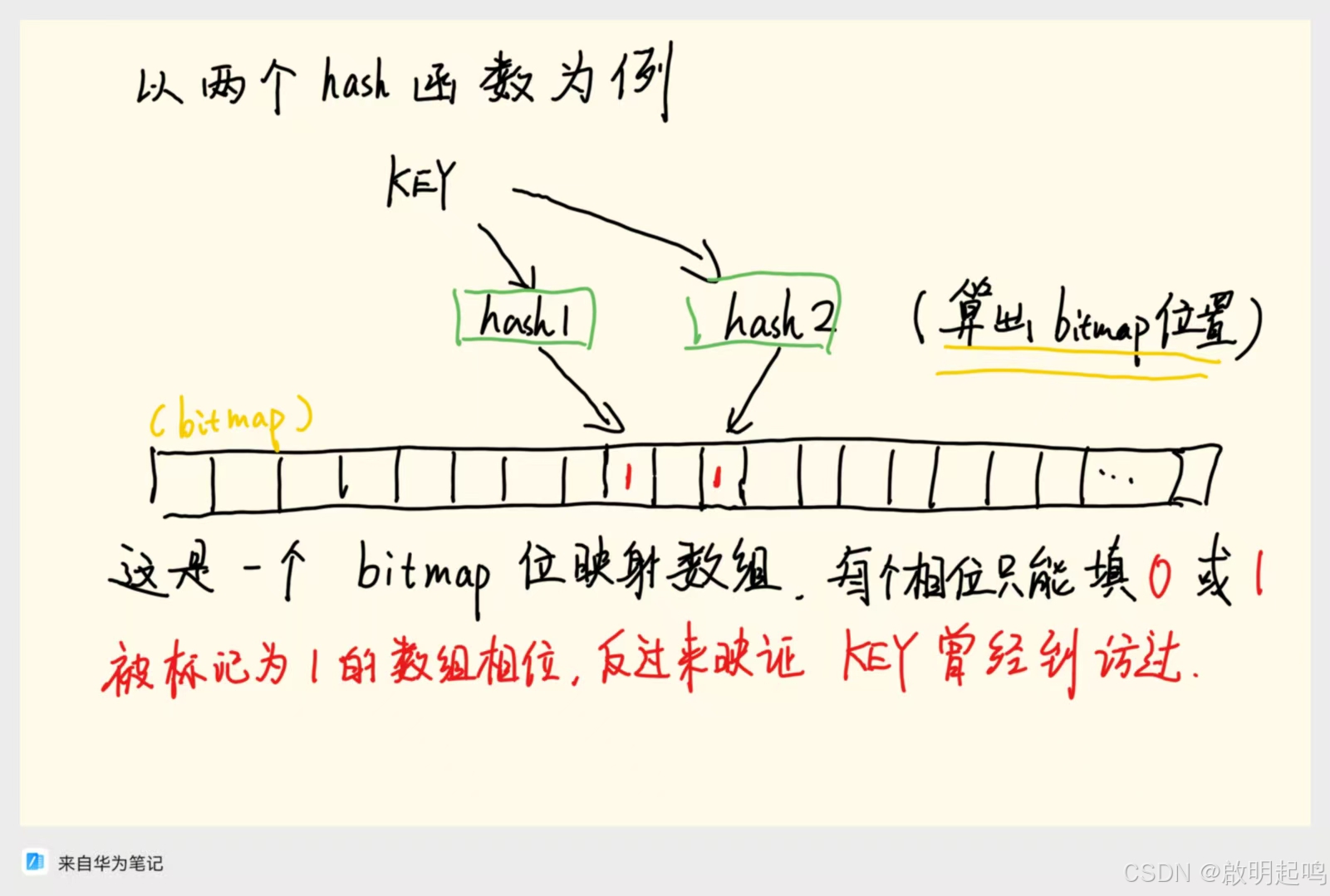
位数组: 布隆过滤器的基础是一个长度为 m 的二进制位数组(初始所有位均为0)。
多个哈希函数: 使用 k 个不同的哈希函数,每个函数都能将输入元素映射到位数组的某个位置(范围在 1 到 m 之间)。我们采用 Hash 函数 来实现位映射 (Bitmap),不光是为了分散,而且还是为了均匀。关键是这个 Hash 函数还得体现均匀分布的随机性,否则就不分散了。我们才用 MurmurHash3 算法。
添加元素:
- 将新元素 x 分别输入这 k 个哈希函数,得到 k 个哈希值 h 1 ( x ) , h 2 ( x ) , . . . , h k ( x ) h_1(x), h_2(x), ..., h_k(x) h1(x),h2(x),...,hk(x)。
- 将位数组中这 k 个位置的值都设置为 1。
查询元素: 将待查询元素 y 分别输入同样的 k 个哈希函数,得到 k 个哈希值 h 1 ( x ) , h 2 ( x ) , . . . , h k ( x ) h_1(x), h_2(x), ..., h_k(x) h1(x),h2(x),...,hk(x)。检查位数组中这 k 个位置的值:
- 如果所有位置的值都是 1,则返回 "可能存在"。
- 如果任何一个位置的值是 0,则返回 "绝对不存在"。
读者可以参考以下这幅图
布隆过滤器是极其节省内存空间的,因为所记录的信息只有是和否(yes or no)而不记录具体的数据,那其实根本用不着结构体,这样安排的话会很紧凑。务必要清楚布隆过滤器是不会存储或加载任何形式的数据。他只是记录一个数据是否来过。
我们采用 Hash 函数 来实现位映射 (Bitmap),不光是为了分散,而且还是为了均匀。关键是这个 Hash 函数还得体现均匀分布的随机性,否则就不分散了。我们才用 MurmurHash3 算法。
关键特性与作用
-
极高的空间效率和查询效率:
空间: 仅需存储一个二进制位数组和几个哈希函数,远小于存储原始数据本身(如 HashSet)的空间需求。例如,处理十亿级别的元素可能只需要几百 MB 到几 GB 内存(具体取决于设定的误判率)。
时间: 添加和查询操作都只需要进行 k 次哈希计算和位数组访问,时间复杂度是常数 O(k),与集合大小无关,速度极快。 -
核心作用:快速过滤"不存在"的元素:
绝对不存在(100%准确) : 如果查询返回"不存在",那么这个元素肯定不在原始集合中。这是布隆过滤器最可靠、最有价值的作用。
可能存在(有一定误判率): 如果查询返回"存在",那么这个元素很可能在原始集合中,但也可能不在(假阳性)。这是布隆过滤器为了节省空间而付出的代价。 -
容忍一定的误判率(假阳性):
这是布隆过滤器的主要缺点。它可能会把原本不在集合中的元素误判为存在。
原因: 哈希冲突。不同的元素经过不同的哈希函数后,可能会将位数组的同一个位置设置为 1。当查询一个新元素时,即使它从未被加入过,如果它对应的 k 个位置恰好都被其他元素设为 1 了,就会被误判为存在。
控制因素: 误判率 p 可以通过以下参数控制:
位数组大小 m: m 越大,误判率越低(空间开销越大)。
哈希函数数量 k: k 需要精心选择(通常 k ≈ (m/n) * ln(2),其中 n 是预估元素数量),k 过多会导致位数组更快被填满(1 变多),反而增加误判率;k 过少则冲突概率增加。
预估元素数量 n: 设计时需要预估 n。实际加入元素数量远超 n 时,误判率会显著上升。
公式(近似): p ≈ (1 - e^(-k * n / m))^k -
无法删除元素(通常):
直接将某个元素对应的位设置为 0 可能会影响到其他共享这些位的元素(导致它们被误判为不存在)。
主要应用场景(利用其"不存在"判断的准确性)
-
缓存穿透防护:
问题: 频繁查询数据库中根本不存在的数据(如非法ID),导致数据库压力过大。
方案: 将缓存过的合法Key加入布隆过滤器。查询时先过布隆过滤器:------返回"不存在":直接拒绝请求,避免访问数据库。
------返回"存在":再去缓存查(缓存没有再去数据库查)。即使有少量误判(合法Key被误判为不存在),最多是访问一次缓存或数据库,影响可控。
-
网络爬虫去重:
问题: 需要避免重复爬取相同的URL。
方案: 将已爬取的URL加入布隆过滤器。遇到新URL:------布隆过滤器说"不存在":一定是新URL,需要爬取。
------布隆过滤器说"存在":可能是已爬过的URL(大概率),也可能是新URL但被误判了(小概率)。为了不遗漏,可以再结合一个更精确(但更慢/更占空间)的机制(如小规模HashSet或数据库)进行二次确认,或者直接爬取(容忍少量重复)。大大减少了需要精确检查的URL数量。
-
垃圾邮件/恶意网站过滤:
将已知的垃圾邮件发件人地址、恶意网站URL加入布隆过滤器。收到邮件或访问链接前先快速过滤掉已知的"坏蛋"。误判(把好邮件/网站误判为坏)需要其他机制兜底(如更复杂的规则或人工审核白名单)。
-
分布式系统:
键值存储: 判断某个键是否可能存在于某个分片或节点上,避免不必要的网络查询。
分布式数据库: 判断某条记录是否可能存在于某个节点。
避免昂贵的查询: 在需要访问慢速存储(如磁盘、网络服务)前,先用布隆过滤器快速过滤掉肯定不存在的数据请求。
推荐系统: 快速过滤掉用户已经看过或明确表示不喜欢的物品ID,避免重复推荐。
布隆过滤器的概率模型(离散的均匀分布)
布隆过滤器的性能(空间效率和误判率)完全由两个关键参数决定:哈希函数的数量 (k) 和位数组的大小 (m)。它们的计算依据是在空间效率和误判率之间进行数学上的最优权衡。我们的目标是:在给定预期元素数量 (n) 和 可接受的最大误判率 ( p ) (p) (p) 的情况下,计算出最小的位数组大小 (m) 和 最优的哈希函数数量 (k)。
我们采用 Hash 函数 来实现位映射 (Bitmap),不光是为了分散,而且还是为了均匀。关键是这个 Hash 函数还得体现均匀分布的随机性,否则就不分散了。我们采用 MurmurHash3 算法。
1、位数组大小 (m) 的计算依据
计算依据: 位数组需要足够大,以避免被过快"填满"。位数组中"1"的密度直接决定了误判率。hash 函数
直观理解: 如果位数组太小,很快就会被大量的 1 填满。当一个新元素来查询时,它对应的 k 个位置很可能已经被其他元素设置为 1 了,导致误判率急剧上升。
数学推导: 假设哈希函数是完全随机的,一个特定的比特位在插入一个元素后没有被某个哈希函数置为 1 的概率是: 1 − 1 m 1 - \frac{1}{m} 1−m1 (这是由于 hash 函数是一个离散的均匀多点分布) 。在插入 n 个元素后,一个特定的比特位仍然为 0 的概率是: ( 1 − 1 m ) k n (1 - \frac{1}{m})^{kn} (1−m1)kn。根据重要极限公式
lim x → ∞ ( 1 − 1 x ) x = 1 e , \lim_{x \to \infty} (1 - \frac{1}{x})^x = \frac{1}{e}, x→∞lim(1−x1)x=e1,
我们可以将其近似为: ( 1 − 1 m ) k n ≈ e − k n / m (1 - \frac{1}{m})^{kn} \approx e^{-kn/m} (1−m1)kn≈e−kn/m,当 m 充分大的时候,这个 m 正是 bitmap 位映射数组的大小。因此,该比特位被置为 1 的概率为: 1 − e − k n / m 1 - e^{-kn/m} 1−e−kn/m。现在,我们想要误判率 p 尽可能低。一个元素被误判,要求其 k 个哈希位置都已经是 1。这个误判概率(成本函数)为:
p ( k , m ) ≈ ( 1 − e − k n / m ) k p(k,m) ≈ (1 - e^{-kn/m})^k p(k,m)≈(1−e−kn/m)k
我们的目标是反解出 m。通过数学优化(对 p 的表达式取对数并求极值),可以得出在最优的哈希函数数量 k 下,m 与 n 和 p 的关系为:
m = − n ln p ( ln 2 ) 2 m = -\frac{n \ln p}{(\ln 2)^2} m=−(ln2)2nlnp
结论: 位数组大小 m 正比于预期元素数量 n,并反比于误判率 p 的自然对数。你希望存储的元素越多 (n 越大),所需的位数组就越大 (m 越大)。你要求的误判率越低 (p 越小),所需的位数组就越大 (m 越大)。例如,将 p 从 1% 降低到 0.1%,m 大约需要增加 50%。
2、哈希函数数量 (k) 的计算依据
计算依据: 哈希函数的数量需要最优化,以最小化误判率。太多了或太少了都会导致问题。
直观理解:
------如果 k 太小(例如只有1个): 哈希冲突的概率很高。不同的元素可能被映射到同一个位置,导致位数组更快被填满,从而增加误判率。
------如果 k 太大: 每个元素都会设置大量的位,会非常快地将位数组"填满",导致位数组迅速变得饱和(几乎全是1)。此时,查询任何元素都会得到"可能存在"的结果,误判率接近100%。
数学推导:
我们从公式出发: p ( k , m ) ≈ ( 1 − e − k n / m ) k p(k,m) ≈ (1 - e^{-kn/m})^k p(k,m)≈(1−e−kn/m)k
通过计算(对 p 关于 k 求导并令导数为零),
∂ ∂ k ⋅ p ( k , m ) = ( 1 − e − k n / m ) k ⋅ ln ( 1 − e − k n / m ) + k ( 1 − e − k n / m ) k − 1 n m e − k n / m , \frac{\partial}{\partial k}\cdot p(k,m) = (1 - e^{-kn/m})^k \cdot \ln(1 - e^{-kn/m}) +k(1 - e^{-kn/m})^{k-1}\frac{n}{m} e^{-kn/m}, ∂k∂⋅p(k,m)=(1−e−kn/m)k⋅ln(1−e−kn/m)+k(1−e−kn/m)k−1mne−kn/m,
令
( 1 − e − k n / m ) ln ( 1 − e − k n / m ) + k n m e − k n / m = 0 (1 - e^{-kn/m})\ln(1 - e^{-kn/m}) + \frac{kn}{m} e^{-kn/m}=0 (1−e−kn/m)ln(1−e−kn/m)+mkne−kn/m=0
可以找到使误判率 p 最小的 k 值(实在不会的话可以代入计算)。这个最优值 k 为:
k = m n ln 2 k = \frac{m}{n} \ln 2 k=nmln2
联立公式,
{ k = m n ln 2 , m = − n ln p ( ln 2 ) 2 . \left\{ \begin{aligned} k = \frac{m}{n} \ln 2, \\ m = -\frac{n \ln p}{(\ln 2)^2}. \end{aligned} \right. ⎩ ⎨ ⎧k=nmln2,m=−(ln2)2nlnp.
我们可以得到直接用 p 表示的 k:
k = − ln p ln 2 k = -\frac{\ln p}{\ln 2} k=−ln2lnp
结论: 最优的哈希函数数量 k 只取决于误判率 p,而与预期元素数量 n 无关。这是一个非常反直觉但重要的结论。 常见的 k 值如下:
| 目标误判率 ( p ) (p) (p) | 最优哈希函数数量 (k) |
|---|---|
| 1% (0.01) | -ln(0.01)/ln(2) ≈ 7 |
| 0.1% (0.001) | -ln(0.001)/ln(2) ≈ 10 |
| 0.01% (0.0001) | -ln(0.0001)/ln(2) ≈ 14 |
C 代码实现
我们需要明确的一点是
数据结构 = 数据定义 + 数据的操作方法。 数据结构 = 数据定义 + 数据的操作方法。 数据结构=数据定义+数据的操作方法。
首先进行数据定义,包括位映射数组,位数组的大小,所采用的 hash 函数数量。
c
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#include <math.h> // 数学库是需要单独链接的 -lm
#include <inttypes.h> // 提供 uint32_t 和 PRIu32
// 布隆过滤器结构体
typedef struct {
uint8_t *bit_array; // 位数组
size_t size; // 位数组大小(比特数)
int num_hashes; // 哈希函数数量
} BloomFilter;Hash 函数是 MurmurHash3-128bit
c
#define ROTL64(x,y) _rotl64(x,y)
#define BIG_CONSTANT(x) (x)
// 64 位循环左移
static inline uint64_t _rotl64(uint64_t x, int8_t r) {
return (x << r) | (x >> (64 - r));
}
// 128位的数,可以看成是 64 位数的二元数组
uint64_t getblock64 ( const uint64_t * p, int i ){
return p[i];
}
// 大数混合器
uint64_t fmix64 ( uint64_t k ) {
k ^= k >> 33;
k *= BIG_CONSTANT(0xff51afd7ed558ccd);
k ^= k >> 33;
k *= BIG_CONSTANT(0xc4ceb9fe1a85ec53);
k ^= k >> 33;
return k;
}
void MurmurHash3_x64_128 ( const void * key, const int len, const uint32_t seed, void * out ) {
const uint8_t * data = (const uint8_t*)key;
const int nblocks = len / 16;
uint64_t h1 = seed;
uint64_t h2 = seed;
const uint64_t c1 = BIG_CONSTANT(0x87c37b91114253d5);
const uint64_t c2 = BIG_CONSTANT(0x4cf5ad432745937f);
//----------
// body
const uint64_t * blocks = (const uint64_t *)(data);
for(int i = 0; i < nblocks; i++)
{
uint64_t k1 = getblock64(blocks,i*2+0);
uint64_t k2 = getblock64(blocks,i*2+1);
k1 *= c1; k1 = ROTL64(k1,31); k1 *= c2; h1 ^= k1;
h1 = ROTL64(h1,27); h1 += h2; h1 = h1*5+0x52dce729;
k2 *= c2; k2 = ROTL64(k2,33); k2 *= c1; h2 ^= k2;
h2 = ROTL64(h2,31); h2 += h1; h2 = h2*5+0x38495ab5;
}
//----------
// tail
const uint8_t * tail = (const uint8_t*)(data + nblocks*16);
uint64_t k1 = 0;
uint64_t k2 = 0;
switch(len & 15)
{
case 15: k2 ^= ((uint64_t)tail[14]) << 48;
case 14: k2 ^= ((uint64_t)tail[13]) << 40;
case 13: k2 ^= ((uint64_t)tail[12]) << 32;
case 12: k2 ^= ((uint64_t)tail[11]) << 24;
case 11: k2 ^= ((uint64_t)tail[10]) << 16;
case 10: k2 ^= ((uint64_t)tail[ 9]) << 8;
case 9: k2 ^= ((uint64_t)tail[ 8]) << 0;
k2 *= c2; k2 = ROTL64(k2,33); k2 *= c1; h2 ^= k2;
case 8: k1 ^= ((uint64_t)tail[ 7]) << 56;
case 7: k1 ^= ((uint64_t)tail[ 6]) << 48;
case 6: k1 ^= ((uint64_t)tail[ 5]) << 40;
case 5: k1 ^= ((uint64_t)tail[ 4]) << 32;
case 4: k1 ^= ((uint64_t)tail[ 3]) << 24;
case 3: k1 ^= ((uint64_t)tail[ 2]) << 16;
case 2: k1 ^= ((uint64_t)tail[ 1]) << 8;
case 1: k1 ^= ((uint64_t)tail[ 0]) << 0;
k1 *= c1; k1 = ROTL64(k1,31); k1 *= c2; h1 ^= k1;
};
//----------
// finalization
h1 ^= len; h2 ^= len;
h1 += h2;
h2 += h1;
h1 = fmix64(h1);
h2 = fmix64(h2);
h1 += h2;
h2 += h1;
((uint64_t*)out)[0] = h1;
((uint64_t*)out)[1] = h2;
}初始化布隆过滤器
布隆过滤器的性能(空间效率和误判率)完全由两个关键参数决定:哈希函数的数量 (k) 和位数组的大小 (m)。它们的计算依据是在空间效率和误判率之间进行数学上的最优权衡。我们的目标是:在给定预期元素数量 (n) 和 可接受的最大误判率 ( p ) (p) (p) 的情况下,计算出最小的位数组大小 (m) 和 最优的哈希函数数量 (k)
布隆过滤器的初始化就是依据前面的概率模型演算------算出需要用多少个 Hash 函数、多长的位映射数组。
c
// 初始化布隆过滤器
BloomFilter *bloom_filter_init(size_t expected_items, double false_positive_rate) {
// 计算最优的位数组大小和哈希函数数量
size_t size = (size_t)(-(expected_items * log(false_positive_rate)) / (log(2) * log(2))); // 会被转化成double
// 负号仅应用于乘积结果,而非元素数量。元素数量(n)永远是正数,取负无意义
// -n 等于 (-n) 导致符号出错,把负数号给吞掉了
int num_hashes = (int)((double)size / expected_items * log(2));
// 确保至少有1个哈希函数
if (num_hashes < 1) num_hashes = 1;
// 分配布隆过滤器结构
BloomFilter *filter = (BloomFilter *)malloc(sizeof(BloomFilter));
if (!filter) return NULL;
// 计算所需的字节数(每个字节8位), 取多一位,使之完全覆盖
size_t num_bytes = (size + 7) / 8;
filter->bit_array = (uint8_t*)calloc(num_bytes, sizeof(uint8_t));
if (!filter->bit_array) {
free(filter);
return NULL;
}
filter->size = size;
filter->num_hashes = num_hashes;
printf("Create Bloomfilter: size = %zu bit, the quantity of hash = %d\n", size, num_hashes);
return filter;
}销毁布隆过滤器
c
// 释放布隆过滤器
void bloom_free(BloomFilter* bf) {
if (bf) {
free(bf->bit_array);
free(bf);
}
}记录数据(记录存在与否而非数据本身)
所谓的插入 insert,其实就是在对应的位映射数组上的某个位置置 1。另外,尽管我们使用多个 hash 函数,但是我们使用的 Murmurhash3 是输出 128 位的,我们只需要把前 64 位和后 64 位以不同的线性组合结合在一起就可以生成不同的随机数,保证随机。这样做是可以简化算法本身的
c
// 设置位,完成位映射,定位到第几个,就让位数组的第几个位设置为 1
static void set_bit(BloomFilter* bf, size_t bit) {
size_t index = bit / 8;
size_t offset = bit % 8;
bf->bit_array[index] |= (1 << offset); // 按位与操作,最高位设置成 1,用作封顶
}
// 检查位,最高位是否设置为 1
static int get_bit(BloomFilter* bf, size_t bit) {
size_t index = bit / 8;
size_t offset = bit % 8;
return (bf->bit_array[index] >> offset) & 1;
}
// 添加元素到布隆过滤器
// 插入元素,并没有实质的插入,知识记录
void bloom_insert(BloomFilter* bf, const void* data, size_t len) {
uint64_t hash[2]; // 这就是 128 位的伪随机大数
MurmurHash3_x64_128(data, len, 0x12345678, hash);
// 使用双重哈希技巧生成多个哈希值
uint64_t h1 = hash[0];
uint64_t h2 = hash[1];
for (int i = 0; i < bf->num_hashes; i++) {
// 计算第i个哈希位置
uint64_t combined = h1 + i * h2;
size_t position = combined % bf->size; // size_t 其实就是无符号 64 位的整数
set_bit(bf, position);
}
}布隆过滤器判断数据是否存在(必须把数据全部插入到位映射数组后才执行)
c
// 检查元素是否存在
int bloom_contains(BloomFilter* bf, const void* data, size_t len) {
uint64_t hash[2];
MurmurHash3_x64_128(data, len, 0x12345678, hash);
uint64_t h1 = hash[0];
uint64_t h2 = hash[1];
for (int i = 0; i < bf->num_hashes; i++) {
uint64_t combined = h1 + i * h2;
size_t position = combined % bf->size;
if (!get_bit(bf, position)) {
return 0; // 元素一定不存在
}
}
return 1; // 元素可能存在(可能有误报)
}根据概率模型计算假阳率
c
// 计算假阳性率
double bloom_false_positive_rate(const BloomFilter* bf, size_t item_count) {
double k = bf->num_hashes;
double m = bf->size; // 位数组的长度,
double n = item_count;
double exponent = -k * n / m;
double probability = pow(1 - exp(exponent), k);
return probability;
}测试代码(主函数)
我们的测试规模是 100。先是插入 100 个元素, "applei" 的格式共 100 个。然后,逐个测试存在性的判断、不存在性的判断。
c
#define test_num 100
int main() {
// 初始化布隆过滤器:预期1000个元素,误判率1%
BloomFilter *filter = bloom_filter_init(100, 0.001);
if (!filter) {
fprintf(stderr, "create error\n");
return 1;
}
size_t test_count = 0; // 假阳率只与插入多少个元素,从而改变位数组的操作有关
// 添加一些元素
char item[15] = {0};
for (int i = 0; i < test_num; i++) {
sprintf(item, "apple%d", i);
bloom_insert(filter, &item +i, strlen(item));
printf("add: %s\n", item);
test_count++;
memset(item, 0, 15);
}
printf("\n check the terms which have been added:\n");
for (int i = 0; i < test_num; i++) {
sprintf(item, "apple%d", i);
int result = bloom_contains(filter, &item +i, strlen(item));
printf("'%s': %s\n", item, result ? "maybe exist" : "not exist");
memset(item, 0, 15);
}
printf("\n check the terms which don't exist:\n");
const char *test_items[] = {"peach", "strawberry", "watermelon", "pineapple"};
for (int i = 0; i < 4; i++) {
int result = bloom_contains(filter, test_items[i], strlen(test_items[i]));
printf("'%s': %s\n", test_items[i], result ? "maybe exist" : "not exist");
}
// 估算误判率
// 估计假阳性率
printf("\nEstimated false positive rate: %.4f%%\n", bloom_false_positive_rate(filter, test_count) * 100); // %% 是转义
bloom_filter_free(filter);
return 0;
}代码运行效果,还OK。
bash
qiming@qiming:~/share/CTASK/data-structure$ gcc -o bloom bloomfilter.c -lm
qiming@qiming:~/share/CTASK/data-structure$ ./bloom
Create Bloomfilter: size = 1437 bit, the quantity of hash = 9
add: apple0
add: apple1
add: apple2
add: apple3
add: apple4
add: apple5
add: apple6
add: apple7
add: apple8
add: apple9
add: apple10
add: apple11
add: apple12
add: apple13
add: apple14
add: apple15
add: apple16
add: apple17
add: apple18
add: apple19
add: apple20
add: apple21
add: apple22
add: apple23
add: apple24
add: apple25
add: apple26
add: apple27
add: apple28
add: apple29
add: apple30
add: apple31
add: apple32
add: apple33
add: apple34
add: apple35
add: apple36
add: apple37
add: apple38
add: apple39
add: apple40
add: apple41
add: apple42
add: apple43
add: apple44
add: apple45
add: apple46
add: apple47
add: apple48
add: apple49
add: apple50
add: apple51
add: apple52
add: apple53
add: apple54
add: apple55
add: apple56
add: apple57
add: apple58
add: apple59
add: apple60
add: apple61
add: apple62
add: apple63
add: apple64
add: apple65
add: apple66
add: apple67
add: apple68
add: apple69
add: apple70
add: apple71
add: apple72
add: apple73
add: apple74
add: apple75
add: apple76
add: apple77
add: apple78
add: apple79
add: apple80
add: apple81
add: apple82
add: apple83
add: apple84
add: apple85
add: apple86
add: apple87
add: apple88
add: apple89
add: apple90
add: apple91
add: apple92
add: apple93
add: apple94
add: apple95
add: apple96
add: apple97
add: apple98
add: apple99
check the terms which have been added:
'apple0': maybe exist
'apple1': maybe exist
'apple2': maybe exist
'apple3': maybe exist
'apple4': maybe exist
'apple5': maybe exist
'apple6': maybe exist
'apple7': maybe exist
'apple8': maybe exist
'apple9': maybe exist
'apple10': maybe exist
'apple11': maybe exist
'apple12': maybe exist
'apple13': maybe exist
'apple14': maybe exist
'apple15': maybe exist
'apple16': maybe exist
'apple17': maybe exist
'apple18': maybe exist
'apple19': maybe exist
'apple20': maybe exist
'apple21': maybe exist
'apple22': maybe exist
'apple23': maybe exist
'apple24': maybe exist
'apple25': maybe exist
'apple26': maybe exist
'apple27': maybe exist
'apple28': maybe exist
'apple29': maybe exist
'apple30': maybe exist
'apple31': maybe exist
'apple32': maybe exist
'apple33': maybe exist
'apple34': maybe exist
'apple35': maybe exist
'apple36': maybe exist
'apple37': maybe exist
'apple38': maybe exist
'apple39': maybe exist
'apple40': maybe exist
'apple41': maybe exist
'apple42': maybe exist
'apple43': maybe exist
'apple44': maybe exist
'apple45': maybe exist
'apple46': maybe exist
'apple47': maybe exist
'apple48': maybe exist
'apple49': maybe exist
'apple50': maybe exist
'apple51': maybe exist
'apple52': maybe exist
'apple53': maybe exist
'apple54': maybe exist
'apple55': maybe exist
'apple56': maybe exist
'apple57': maybe exist
'apple58': maybe exist
'apple59': maybe exist
'apple60': maybe exist
'apple61': maybe exist
'apple62': maybe exist
'apple63': maybe exist
'apple64': maybe exist
'apple65': maybe exist
'apple66': maybe exist
'apple67': maybe exist
'apple68': maybe exist
'apple69': maybe exist
'apple70': maybe exist
'apple71': maybe exist
'apple72': maybe exist
'apple73': maybe exist
'apple74': maybe exist
'apple75': maybe exist
'apple76': maybe exist
'apple77': maybe exist
'apple78': maybe exist
'apple79': maybe exist
'apple80': maybe exist
'apple81': maybe exist
'apple82': maybe exist
'apple83': maybe exist
'apple84': maybe exist
'apple85': maybe exist
'apple86': maybe exist
'apple87': maybe exist
'apple88': maybe exist
'apple89': maybe exist
'apple90': maybe exist
'apple91': maybe exist
'apple92': maybe exist
'apple93': maybe exist
'apple94': maybe exist
'apple95': maybe exist
'apple96': maybe exist
'apple97': maybe exist
'apple98': maybe exist
'apple99': maybe exist
check the terms which don't exist:
'peach': not exist
'strawberry': not exist
'watermelon': not exist
'pineapple': not exist
Estimated false positive rate: 0.1025%
qiming@qiming:~/share/CTASK/data-structure$