摘要
本周系统学习了TensorFlow深度学习框架与状态空间模型理论。深入掌握了TensorFlow张量操作机制与tf.keras高级API的使用流程,包括模型构建、训练配置、回调函数应用及模型保存方法;重点研究了状态空间模型的数学原理,解析了连续时间系统中状态方程与输出方程的表示形式,理解了参数矩阵A/B/C/D在系统动态预测中的作用机制,建立了从深度学习框架到动态系统建模的完整知识体系。
Abstract
This week focused on TensorFlow framework and state space model theory. Systematically covered TensorFlow's tensor operations and tf.keras high-level API workflows, including model construction , training configuration , callback applications, and model saving methods. Emphasis was placed on the mathematical principles of state space models, analyzing the representation forms of state and output equations in continuous-time systems, and understanding the role of parameter matrices A/B/C/D in system dynamics prediction, establishing a complete knowledge system from deep learning frameworks to dynamic system modeling.
1、TensorFlow学习
1.1 张量及其操作
1.1.1 张量Tensor
张量是一个多维数组。 与NumPy ndarray对象类似,tf.Tensor对象也具有数据类型和形状。如下图所示:
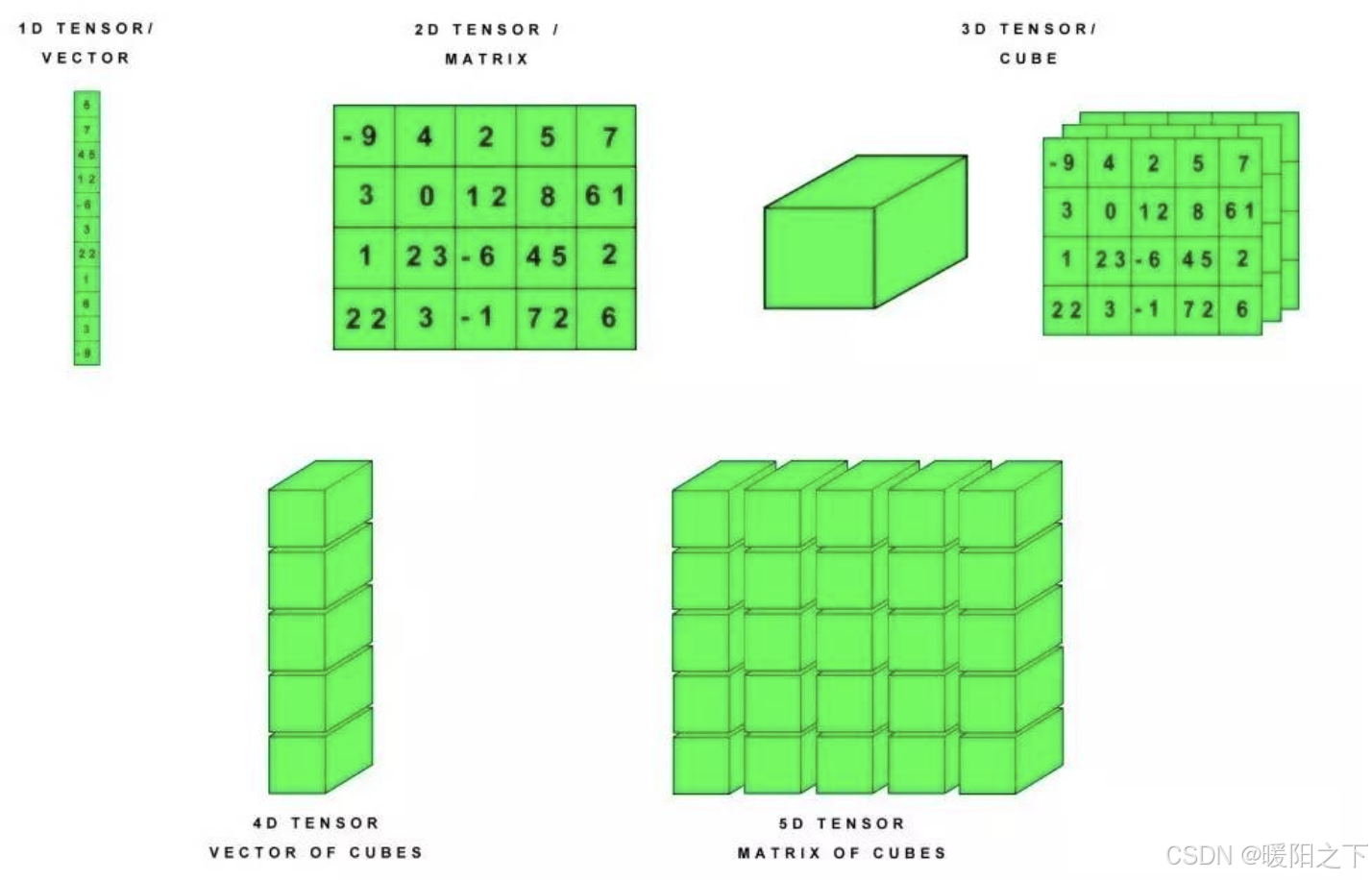
此外,tf.Tensors 可以保留在GPU中。 TensorFlow提供了丰富的操作库(tf.add,tf.matmul,tf.linalg.inv等),它们使用和生成tf.Tensor。在进行张量操作之前先导入相应的工具包:
import tensorflow as tf
import numpy as np1.1.2 基本方法
首先让我们创建基础的张量:
# 创建int32类型的0维张量,即标量
rank_0_tensor = tf.constant(4)
print(rank_0_tensor)
# 创建float32类型的1维张量
rank_1_tensor = tf.constant([2.0, 3.0, 4.0])
print(rank_1_tensor)
# 创建float16类型的二维张量
rank_2_tensor = tf.constant([[1, 2],
[3, 4],
[5, 6]], dtype=tf.float16)
print(rank_2_tensor)输出结果为:
tf.Tensor(4, shape=(), dtype=int32)
tf.Tensor([2. 3. 4.], shape=(3,), dtype=float32)
tf.Tensor(
[[1. 2.]
[3. 4.]
[5. 6.]], shape=(3, 2), dtype=float16)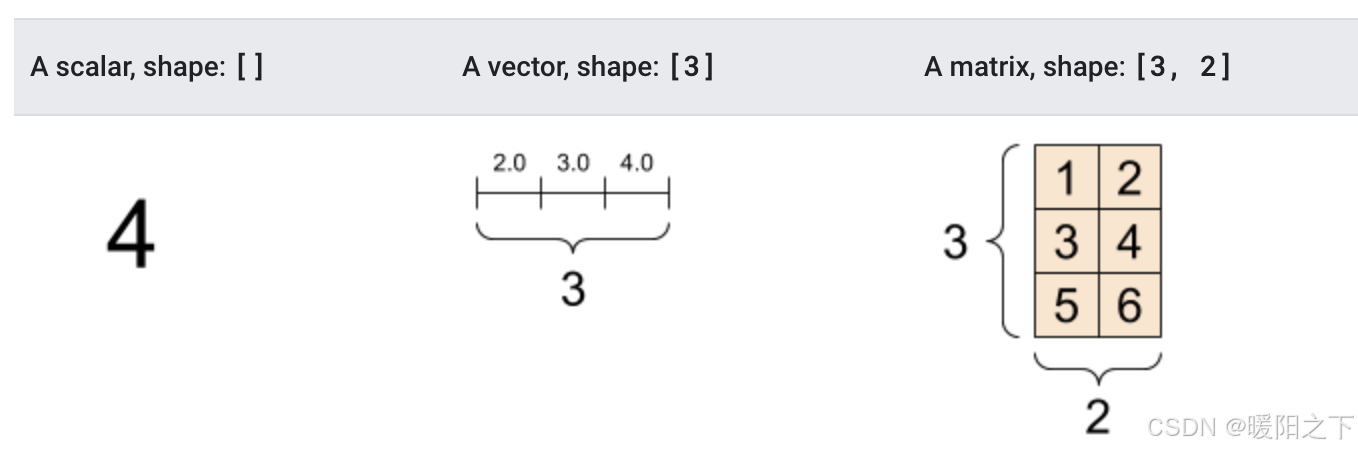
也可以创建更高维的张量:
# 创建float32类型的张量
rank_3_tensor = tf.constant([
[[0, 1, 2, 3, 4],
[5, 6, 7, 8, 9]],
[[10, 11, 12, 13, 14],
[15, 16, 17, 18, 19]],
[[20, 21, 22, 23, 24],
[25, 26, 27, 28, 29]],])
print(rank_3_tensor)该输出结果我们有更多的方式将其展示出来:
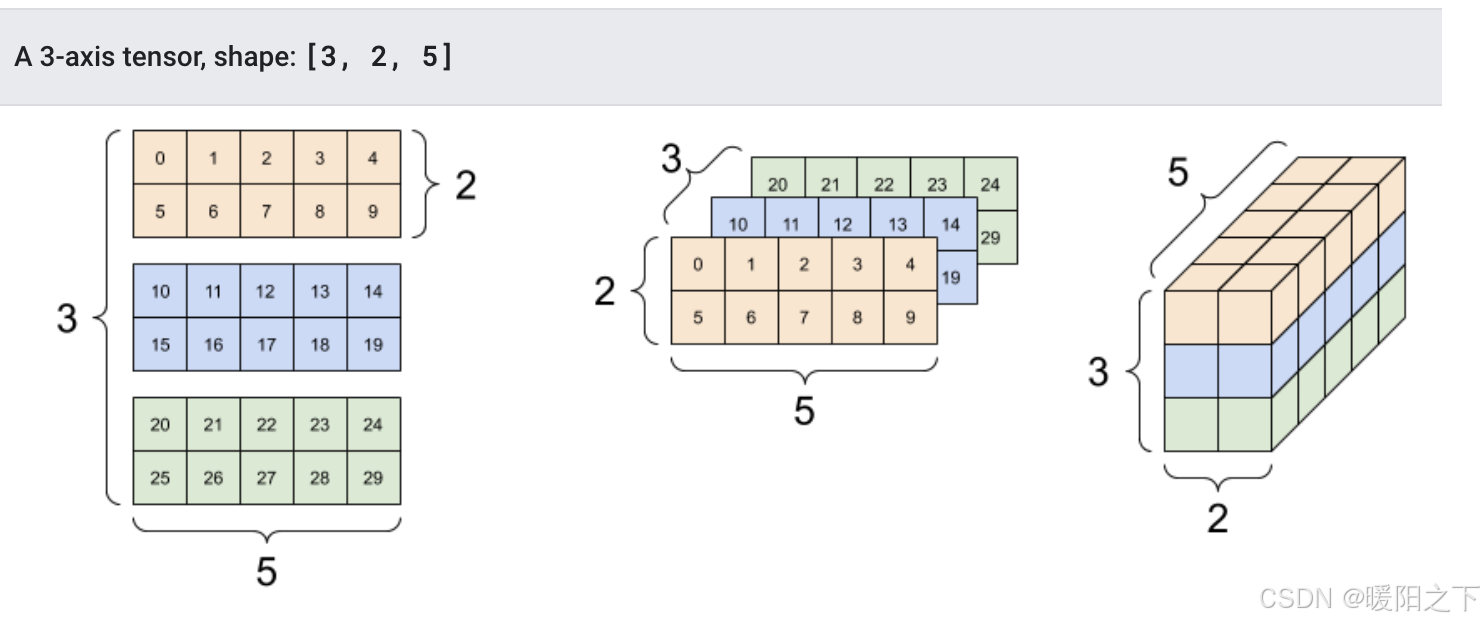
1.1.3 转换成numpy
我们可将张量转换为numpy中的ndarray的形式,转换方法有两种,以张量rank_2_tensor为例:
np.array(rank_2_tensor)
rank_2_tensor.numpy()1.2 tf.keras
f.keras是TensorFlow 2.0的高阶API接口,为TensorFlow的代码提供了新的风格和设计模式,大大提升了TF代码的简洁性和复用性,官方也推荐使用tf.keras来进行模型设计和开发。
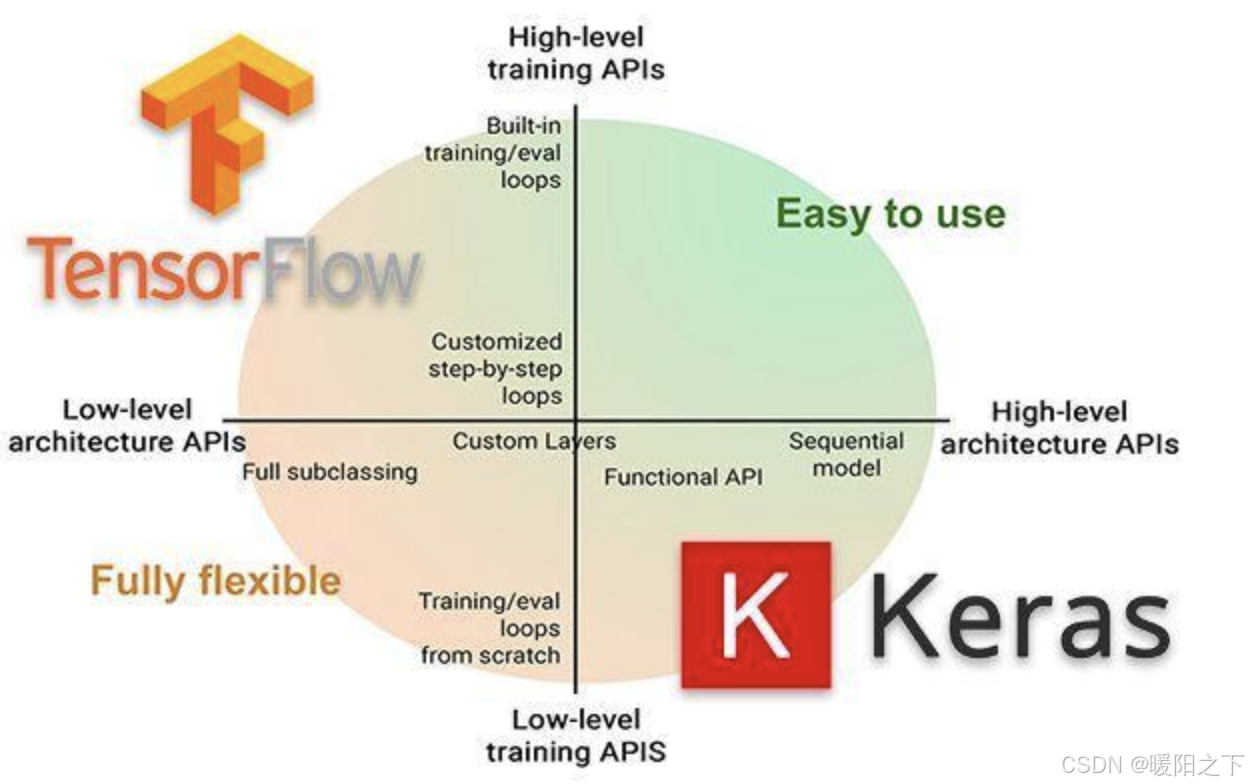
1.2.1 常用模块
tf.keras中常用模块如下表所示:
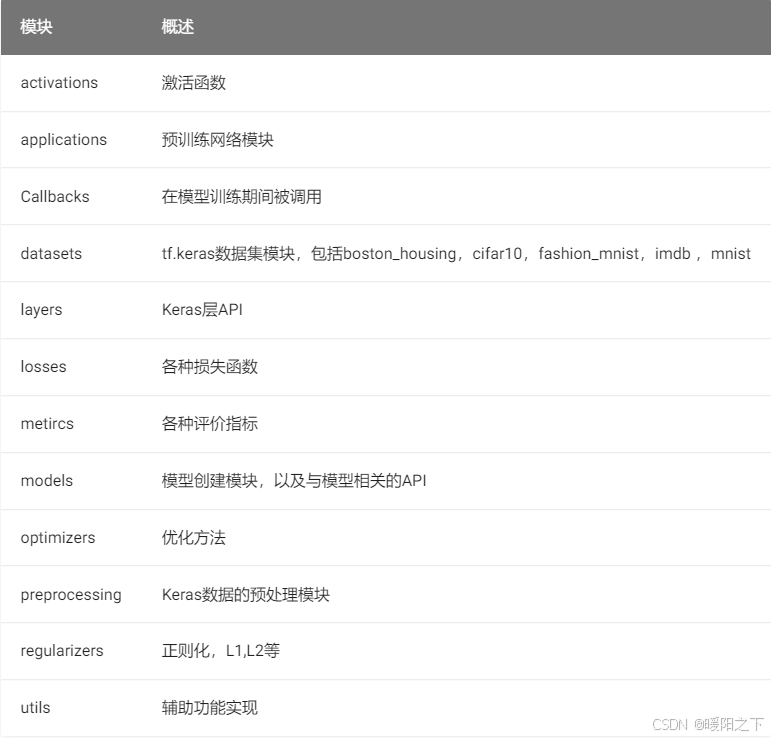
1.2.2 常用方法
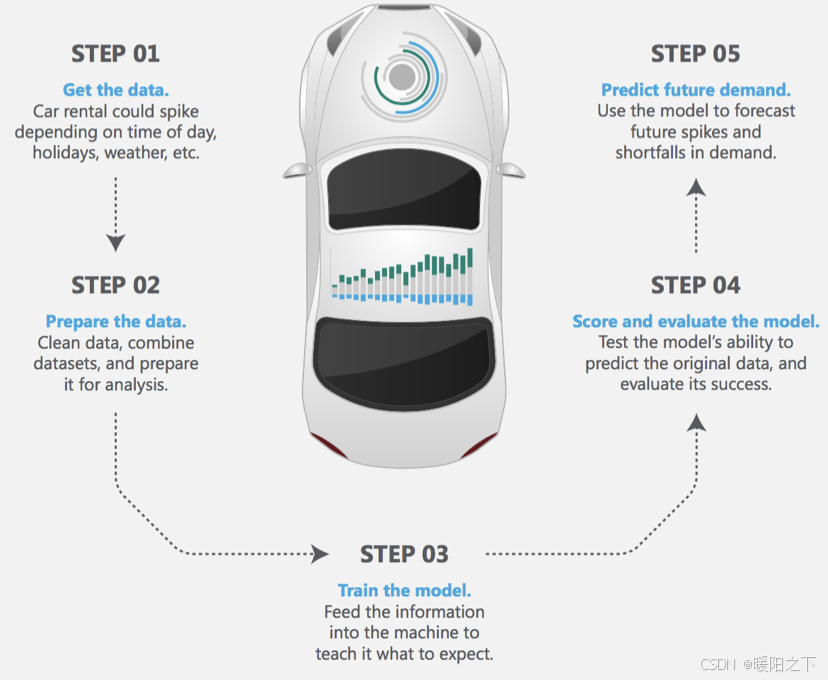
深度学习实现的主要流程:1.数据获取,2,数据处理,3.模型创建与训练,4 模型测试与评估,5.模型预测
1.导入tf.keras
使用 tf.keras,首先需要在代码开始时导入tf.keras
import tensorflow as tf
from tensorflow import keras2.数据输入
对于小的数据集,可以直接使用numpy格式的数据进行训练、评估模型,对于大型数据集或者要进行跨设备训练时使用tf.data.datasets来进行数据输入。
3.模型构建
-
简单模型使用Sequential进行构建
-
复杂模型使用函数式编程来构建
-
自定义layers
4.训练与评估 -
配置训练过程:
配置优化方法,损失函数和评价指标
model.compile(optimizer=tf.train.AdamOptimizer(0.001),
loss='categorical_crossentropy',
metrics=['accuracy']) -
模型训练
指明训练数据集,训练epoch,批次大小和验证集数据
model.fit/fit_generator(dataset, epochs=10,
batch_size=3,
validation_data=val_dataset,
) -
模型评估
指明评估数据集和批次大小
model.evaluate(x, y, batch_size=32)
-
模型预测
对新的样本进行预测
model.predict(x, batch_size=32)
5.回调函数(callbacks)
回调函数用在模型训练过程中,来控制模型训练行为,可以自定义回调函数,也可使用tf.keras.callbacks 内置的 callback :
ModelCheckpoint:定期保存 checkpoints。 LearningRateScheduler:动态改变学习速率。 EarlyStopping:当验证集上的性能不再提高时,终止训练。 TensorBoard:使用 TensorBoard 监测模型的状态。
6.模型的保存和恢复
-
只保存参数
只保存模型的权重
model.save_weights('./my_model')
加载模型的权重
model.load_weights('my_model')
-
保存整个模型
保存模型架构与权重在h5文件中
model.save('my_model.h5')
加载模型:包括架构和对应的权重
model = keras.models.load_model('my_model.h5')
2、状态空间模型 (The State Space Model, SSM)
2.1 状态空间 (State Space)
举个例子:假如我们在走迷宫,那么状态空间(state space)就是我们在地图中所有可能的状态(states), 包含{ 我们正在哪里?下一步可以往哪个方向走走?下一步我们可能在哪里?}
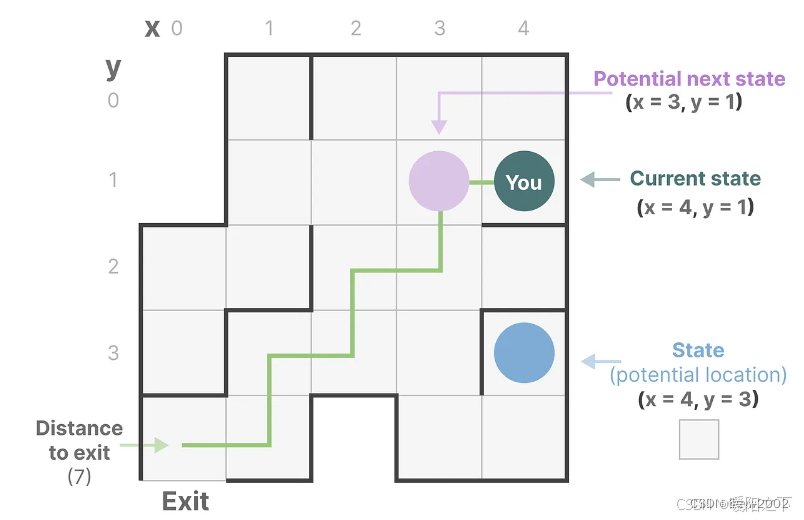
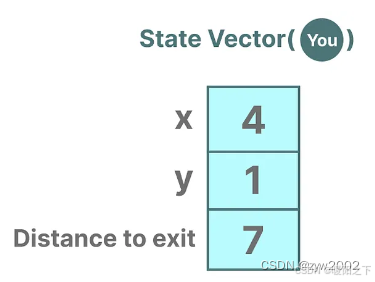
描述状态的变量,在我们的例子中是X和Y坐标,以及到出口的距离,可以表示为"状态向量"。
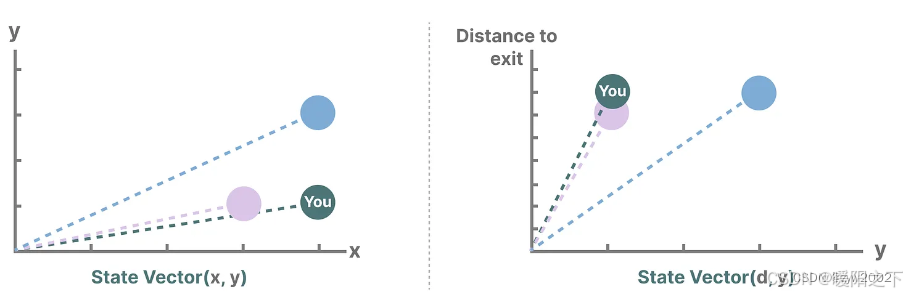
例如,当前的状态向量如下:
2.2 状态空间模型(State Space Model, SSM)
ssm是用于描述这些状态表示的模型,并根据某些输入预测其下一个状态可能是什么。
在时刻t, SSMs为:
- 映射输入序列x(t) -(例如,在迷宫中向左和向下移动)
- 到隐藏状态表示h(t) -(例如,到出口的距离和x/y坐标)
- 并推导出预测的输出序列y(t) -(例如,再次向左移动以更快地到达出口)
然而,SSM不是使用离散序列(如向左移动一次),而是将连续序列作为输入,并预测输出序列。

SSM假设动态系统,例如在3D空间中运动的物体,可以通过两个方程从其在时间t tt的状态进行预测。

2.3 状态方程和输出方程
状态方程:
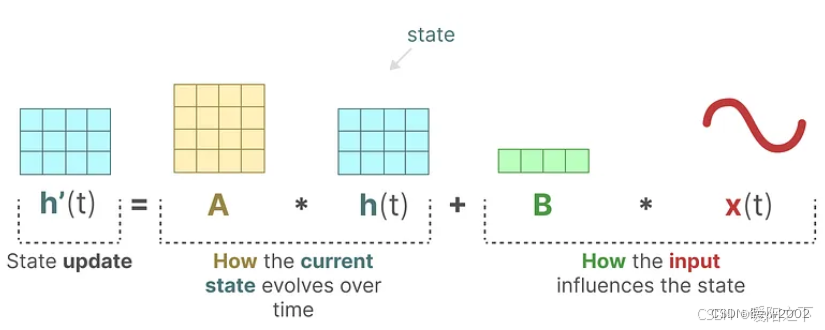
输出方程:
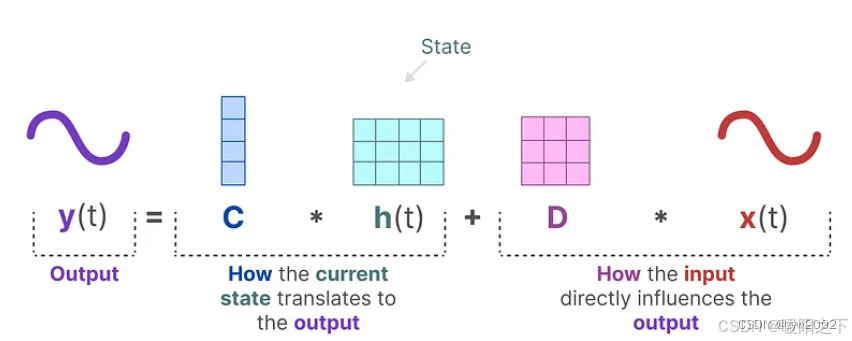
上述的A,B,C,D都是可学习的参数
将上述的两个方程整合在一起,得到了如下的结构:
接下来,我们逐步理解这些矩阵是如何影响学习过程。
Step1: 假设我们有一些输入信号x(t),这个信号首先乘以矩阵B,矩阵B描述了输入如何影响系统。
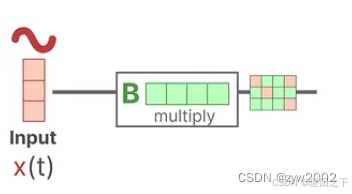
Step 2: 矩阵A和当前状态相乘。矩阵A描述了内部状态之间是如何连接的。
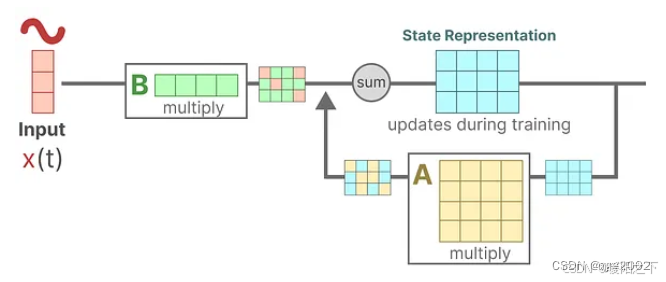
Step 3:矩阵C和新的状态相乘。矩阵C描述了状态是如何转化到输出的。
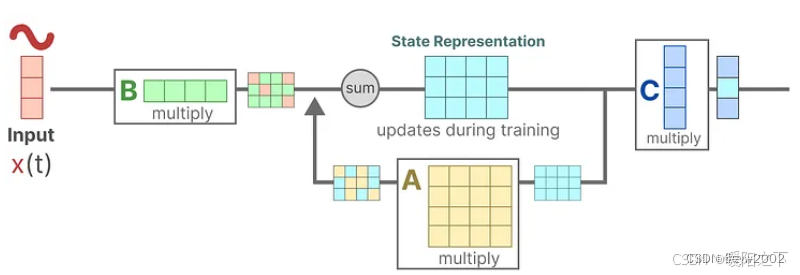
最后,我们可以利用矩阵D提供一个从输入到输出的直接信号。这通常也称为跳跃连接(skip-connection)。
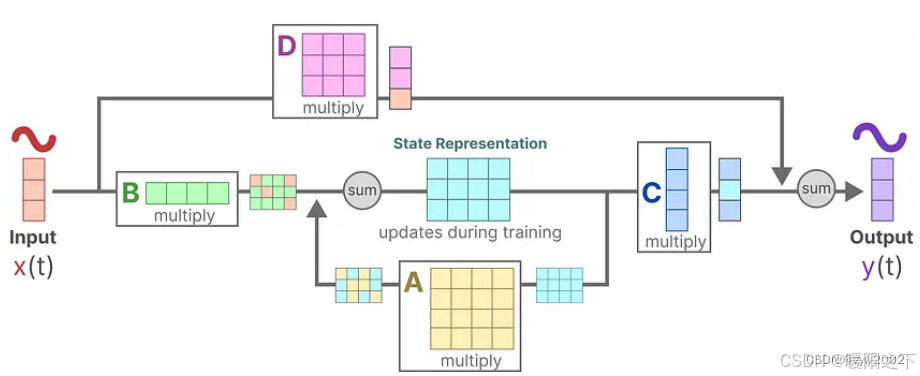
SSM通常被认为是不包含跳跃连接的部分。
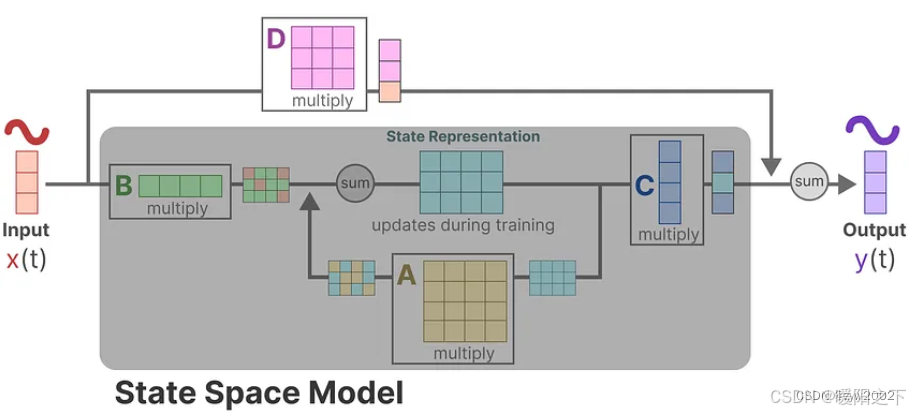
回到我们简化的视角,可以看出矩阵A、B和C是SSM的核心。
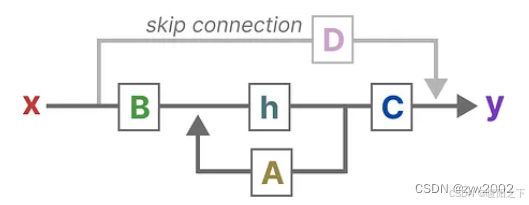
与此同时,可以将原来的两个方程进行新的可视化。
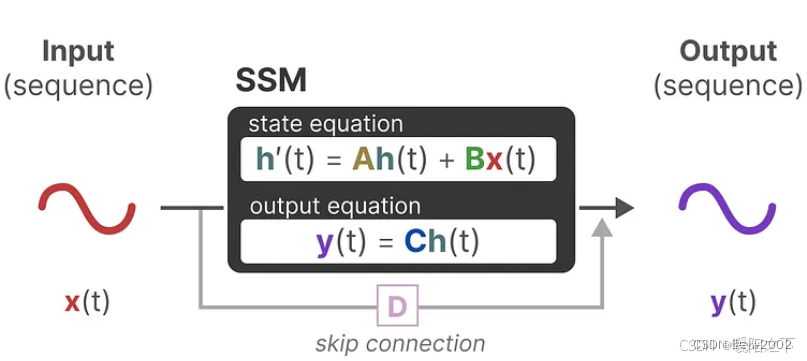
这两个方程旨在从观测数据中预测系统的状态。由于预期输入是连续的,所以SSM的主要表示是连续时间表示(continuous-time representation)。
总结
本周通过理论与实践相结合的方式构建了完整的技术栈:在框架应用层面,系统掌握了TensorFlow的张量创建、numpy转换及tf.keras的开发范式;在理论模型层面,深入理解了状态空间模型的数学本质。