全文 part1 - DGEMM Using Tensor Cores, and Its Accurate and Reproducible Versions

摘要

本文提出了一种在 NVIDIA 图形处理器（GPU）的张量核心（Tensor Cores，仅含 FP16、INT8 等 GEMM 计算功能）上实现 FP64 （双精度，DGEMM ）和 FP32 （单精度，SGEMM ）稠密矩阵乘法的方法。Tensor Cores 是一种特殊的处理单元，可对 FP16 输入执行 4x4 矩阵乘法并以 FP32 精度运算，最终返回 FP32 精度的结果。该方法采用 Ozaki 方案 ------ 一种基于无误差变换的精确矩阵乘法算法 。所提方法具有三大显著优势：其一，可基于 cuBLAS 库的 cublasGemmEx 例程，借助 Tensor Cores 操作构建；其二，能实现比标准 DGEMM 更高的精度，包括正确舍入结果；其三，即便核心与线程数量不同，也能确保位级可复现性。

该方法的可达性能取决于输入矩阵各元素的绝对值范围。例如，当矩阵以动态范围为 1E+9 的随机数初始化时，在 Titan RTX GPU （Tensor Cores 算力为 130 TFlops ）上，我们实现的等效 DGEMM 操作可达约 980 GFlops 的 FP64 运算性能，而 cuBLAS 库的 cublasDgemm 在 FP64 浮点单元上仅能达到 539 GFlops 。研究结果表明，可利用 FP32 /FP64 资源有限但低精度处理单元（如面向 AI 的处理器）运算速度快的硬件，来处理通用工作负载。

关键词 ：Tensor Cores ；FP16 ；半精度；低精度；矩阵乘法；GEMM；线性代数；精度；可复现性

1. 引言

近年来，深度学习 应用的日益增多推动了特殊处理单元的发展，例如 NVIDIA GPU 上的 Tensor Cores 以及谷歌的张量处理单元（TPUs ）。此类任务的核心是矩阵乘法，其并不需要 IEEE 754-2008 binary32 （即单精度，FP32 ，含 8 位指数和 23 位尾数）和 binary64 （即双精度，FP64 ，含 11 位指数和 52 位尾数）这样的高精度。相应地，硬件更支持快速的低精度运算，如 binary16 （即半精度，FP16 ，含 5 位指数和 10 位尾数）以及 INT8 /INT16 位整数运算。

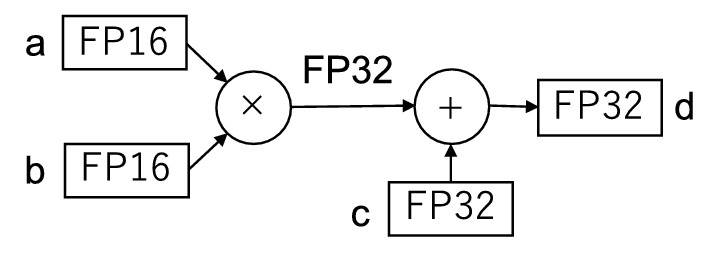
一个广为熟知的例子是 Volta 架构中引入的 Tensor Cores ，其每时钟周期可通过融合乘加操作完成一次 4x4 矩阵乘法。尽管 Tensor Cores 支持多种数据格式和计算精度，但本文聚焦于 FP32 精度模式下的 FP16 计算 ------ 该模式以 FP32 精度执行 运算（图 1 ）。其中， 和 为 FP16 值， 和 为 FP32 值。Tensor Cores 的运算速度最高可达 CUDA 核心上标准 FP32 浮点单元（FPUs ）的 8 倍【注，这里是指fp16 tensorcore gemm 算力，是fp32 cuda core gemm 算力的8倍 ，比如分别为 112TF 和 14 TF】。已有诸多研究在通用任务中充分利用了 Tensor Cores 的这一卓越性能。

本文提出一种在 Tensor Cores 上计算 Level-3 基本线性代数子程序（BLAS ）中通用矩阵乘法例程（GEMM ）的方法，可支持 FP64 （DGEMM ）和 FP32 （SGEMM ）精度。GEMM 是众多科学计算工作负载以及高性能 Linpack 测试中的核心操作之一。该方法基于 Ozaki 等人提出的一种基于无误差变换的精确矩阵乘法算法（亦称 Ozaki 方案 ）[13]。该方法的优势如下：

• 高效实用 ：基于 NVIDIA 提供的 cuBLAS 库中的 cublasGemmEx 例程构建，开发成本低；
• 精度更高 ：即便采用正确舍入，也能实现比标准 SGEMM 和 DGEMM 更高的精度；
• 可复现性强 ：对于相同输入，即便每次执行时核心与线程数量不同，也能得到相同 （位级一致）的结果；
• 适应性好 ：其理念可适配其他精度场景。

部分研究通过利用低精度硬件来加速无需高精度的计算，而本文则尝试借助低精度硬件实现更高精度的计算。我们的 DGEMM 实现仅在 FP64 支持有限的处理器上性能优于 cuBLAS 的 DGEMM 。但相比之下， FP64 浮点单元的性能提升并非关键，更重要的是旨在提升低精度硬件 （如面向人工智能的处理器）的潜力。此外，该方法为兼顾 AI 与传统高性能计算（HPC ）工作负载的高效硬件设计提供了新视角 。例如，可减少 FP64 资源数量，转而提供大规模低精度支持。

本文其余部分结构如下：第 2 节 介绍相关工作；第 3 节 阐述基于 Ozaki 方案的方法；第 4 节 介绍该方法的实现；第 5 节 在 Titan RTX 和 Tesla V100 GPU 上进行精度与性能评估；第 6 节 探讨基于该方法的未来硬件设计方向；第 7 节总结全文。

2. 相关工作

已有多项研究尝试将为 AI 工作负载设计的低精度硬件用于其他场景。例如，Haidar 等人 [7] 在稠密与稀疏线性系统中，结合迭代精化技术利用了标准 FP16 和 FP32 精度模式下的 Tensor Cores 操作。还有研究针对能效提升展开探讨 [6] ，Carson 与 Higham 则对此进行了误差分析 [1] 。Yang 等人 [16] 在谷歌 TPUs 上采用 bfloat16 （BF16 ，含 8 位指数和 7 位尾数）实现了伊辛模型 的蒙特卡洛模拟 。这些研究将低精度运算应用于代码中无需高精度的部分 ------ 此类部分可在该精度水平下完成计算，因此其适用性取决于具体算法或问题。

与本文类似，部分研究尝试借助低精度硬件实现比硬件原生精度更高的运算。例如**，Markidis 等人 [11] 提出了一种提升 Tensor Cores 矩阵乘法计算精度的方法。尽管其方法在概念上与本文相似** ，但仅能对 FP16 支持的动态范围内的矩阵进行计算，且精度与 SGEMM 相当。Henry 等人 [8] 探讨了在 BF16 浮点单元上采用双双精度算术 [2] （一种经典的二重精度算术技术）执行高精度运算的性能。Sorna 等人 [15] 提出了一种****提升张量核心上二维快速傅里叶变换精度的方法。需注意的是，这些研究中，获得超过 FP32 或 FP64 浮点单元的性能并非关键，重点同样在于提升低精度硬件的潜力。因此，可能需要重新设计硬件，以平衡浮点单元所支持的精度。本文的探讨方向与之相近。

本文所提方法的核心 ------**Ozaki 方案，最初是为通过标准浮点运算实现精确矩阵乘法而提出的。**OzBLAS [12] 基于 Ozaki 方案在 CPU 和 GPU 上实现了精确且可复现的 BLAS 例程。OzBLAS 基于 FP64 浮点单元上的 DGEMM 构建【注，结果的精度高于原始的 FP64 gemm】，而本文中的 Ozaki 方案则借助 Tensor Cores 上的 GEMM 执行 DGEMM /SGEMM 操作。Ichimura 等人 [10] 还报道了在多核 CPU 上基于 FP64 运算的 Ozaki 方案高性能实现。

3. 方法

本节首先介绍通过改进的 Ozaki 方案在 Tensor Cores 上计算 DGEMM 的基本方案，随后 介绍用于提升计算速度的附加技术。本文中， 和 分别表示 FP64 和 FP32 算术下的计算【注，数字计算机的 FP64 计算 】； 和 分别表示 FP64 （）和 FP32 （ ）的单位舍入误差【注, 单位舍入误差解释】； 和 分别表示 FP64 和 FP16 浮点数的集合； 表示包含零的自然数集合。

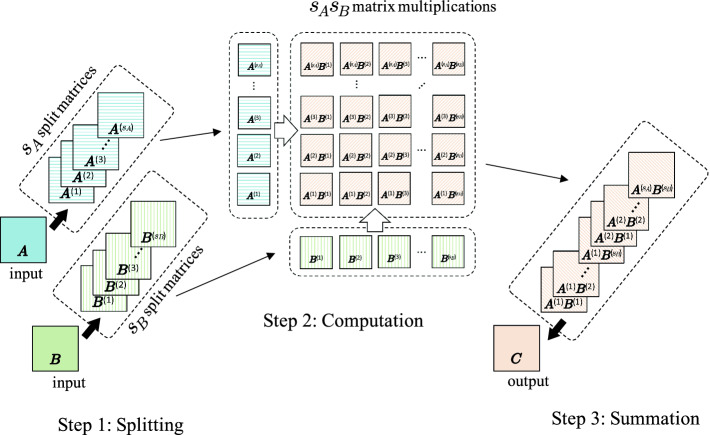
Fig. 2. Schematic of matrix multiplication () by Ozaki scheme (in this figure, scaling is omitted).

3.1 适用于张量核心的 Ozaki 方案

Ozaki 方案对矩阵乘法进行无误差变换，具体而言，将矩阵乘法转化为多个矩阵乘法的求和------ 这些矩阵乘法可通过浮点运算执行且无舍入误差。图 2 为整个 Ozaki 方案的示意图，该方法包含三个主要步骤：

1. 拆分：对输入矩阵按元素拆分得到多个子矩阵；
2. 计算 ：计算所有子矩阵间的两两矩阵乘积；
3. 求和 ：对上述 所有子矩阵间的两两矩阵乘积 按元素求和。

下面详细描述各步骤。为简洁起见，我们以两个向量 的内积为例 进行说明，但该方法可自然扩展到矩阵乘法（矩阵乘法本质上由多个内积构成）。此外，尽管此处仅描述 DGEMM 的情况，但其理念同样适用于 SGEMM。

步骤 1：拆分 。算法 1 将 FP64 输入向量拆分为多个 FP16 向量，过程如下：

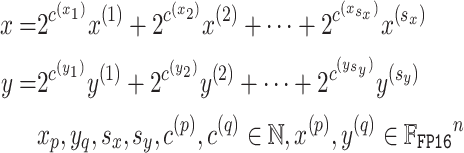
首先得到 FP64 格式的子向量，再将其转换（降尺度）为 FP16 格式。该转换仅调整指数，不会导致有效数字的 bit 丢失。其中， 和 分别为向量 和 的指数从 FP64 到 FP16 的缩小因子。在算法 1 的第 7 行 中，当 时， 达到 1024 ，这意味着 和 可存储为 2 字节 short 类型的整数。拆分算法需满足以下特性：

1. 若 和 为非零元素，则

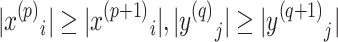
2. 在 FP32 计算中必须无误差：

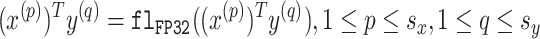
拆分可理解为从浮点表示到定点表示的转换。上述第一个特性意味着，通过省略最低阶的部分子向量，可控制最终结果的精度（降低精度）。在一定数量的子向量下可获得的最终结果精度，取决于内积的长度以及输入向量各元素的绝对值范围。需注意的是，若要将 Tensor Cores 替换为其他精度的浮点单元，需修改算法 1 中的参数 ，且被分割的向量（ 和 ）的 bit 数取决于浮点单元的精度。

步骤 2：计算 。接下来，内积 按如下方式计算：

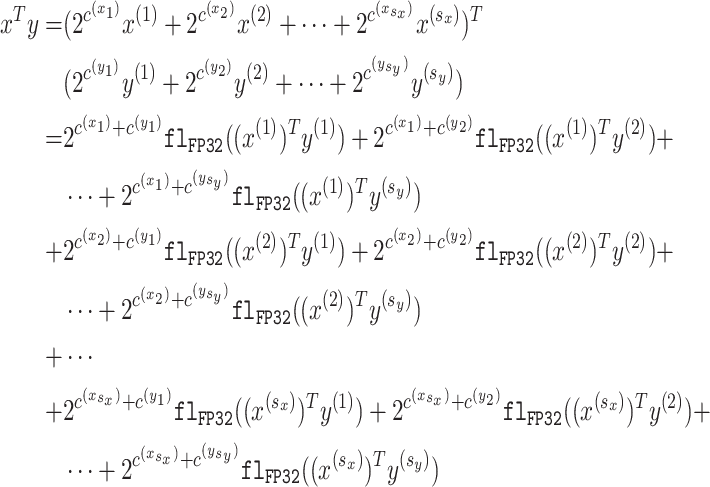
此处需计算子向量间所有两两内积，共需计算 个内积。 为放大因子，用于补偿拆分过程中的缩小操作。根据算法 1 的第二个特性，由于输入为 FP16 格式，子向量的内积可通过Tensor Core 操作计算。将该示例扩展到矩阵乘法时，必须基于标准内积算法对子矩阵进行乘法 ------ 不允许采用 Strassen 算法等分治方法。

步骤 3：求和 。最后，对子向量的内积进行求和。若所需精度为标准 DGEMM 的精度，求和可通过 FP64 算术完成。但由于步骤 2 中的 无舍入误差（无误差），通过例如 NearSum [14] 等正确舍入方法进行求和，可得到 的正确舍入结果。即便在 FP64 算术中，若采用可复现的求和方法，结果也具有可复现性。由于求和是按元素进行的，计算顺序易于固定。

矩阵乘法的完整流程 。算法 2 在 Tensor Cores 上实现了矩阵乘法的完整 Ozaki 方案 。其中，SplitA 和 SplitB 分别沿矩阵 和 的内积方向（k 维），采用算法 1 进行拆分。需注意的是，由于 和 可存储为 FP16 格式， 可通过 cuBLAS 库的 cublasGemmEx 例程，在 Tensor Core 上以 FP32 精度执行 FP16 计算。

3.2 快速计算技术

为进一步提升性能，可通过以下方法修改算法 1 或算法 2 。第 4 节 将讨论不改变算法的基于实现的加速技术。

快速模式 。与 OzBLAS 的实现类似，我们定义参数 来确定计算中子矩阵的数量。指定后，可通过省略 中 的计算来减少计算量，但会导致精度略有损失。若所需精度为 FP64 （与标准 DGEMM 相当，通过下述确定子矩阵数量的方法实现），则精度损失可忽略不计。该技术最多可将矩阵乘法的数量从 减少到 。

估算实现 FP64 等效精度所需的子矩阵数量 。算法 1在 时会自动停止拆分，即此时最终结果的精度达到最大。但如果所需精度为 FP64 算术下标准 DGEMM 的精度（FP64 等效精度），可基于概率误差界 [9] 通过算法 3 估算所需的最小拆分次数：

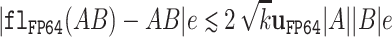
其中， 的引入是为了避免在估算中进行矩阵乘法（需注意，在算法 3 的第 7 行 中 ，为第 d 个 未缩小的 FP64 子矩阵。因此，第 2 行 的 SplitA 到 无需执行到，且可将 SplitA 与该算法集成）。该算法设计用于快速模式。若拆分次数按算法 1 执行到的方式确定，精度可能低于标准 DGEMM 。此时，必须禁用快速模式。需注意的是，由于子矩阵数量仅基于概率误差界估算 ，且会受向量 影响，该方法中期望精度 （标准 DGEMM 所达精度）与实际获得精度之间可能存在一定差异。

内积分块 。本研究暂未实现此步骤。由于算法 1 中的 包含内积维度 ，实现一定精度所需的拆分次数取决于矩阵的内积维度。通过对内积操作采用分块策略 ，可避免拆分次数的增加。分块大小可设置为实现最佳性能的最小尺寸。但该策略会增加求和成本 ，且除非执行正确舍入计算，否则改变分块大小可能会影响可复现性。