首先我们要知道深度学习和机器学习的关系------深度学习(DL, Deep Learning)是机器学习(ML, Machine Learning)领域中一个新的研究方向。
深度学习简介
我理解的深度学习就通过多层感知器，对数据进行训练，可以达到非线性变换，如何可以提取非线性的特征，深度学习里面这个多层结构叫做神经网络，我们先了解下人的神经网络。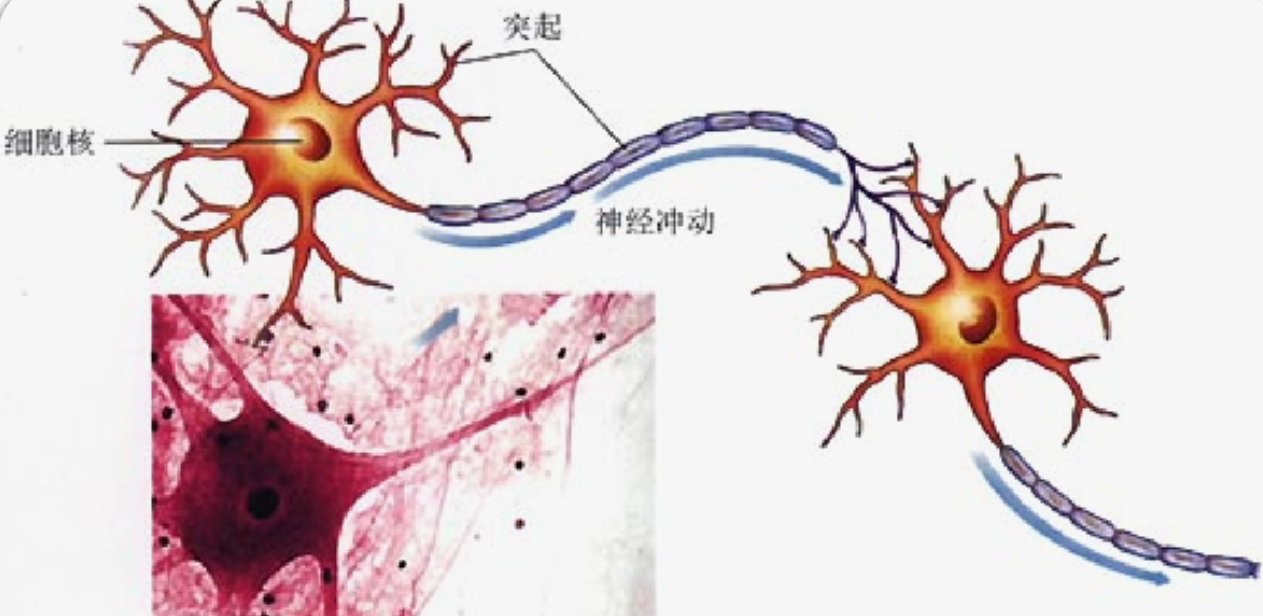
就是有神经元，如何有突触进行连接，如何就可以传递信息了，那么我们取这个名字肯定和这个原理差不多的。
原理介绍
首先我们先以一层的来进行分析，就是把所有特征加上权重然后相加，最后进行非线性变换，然后再传给下一个神经元，这样我们就完成了第一次非线性变换了。
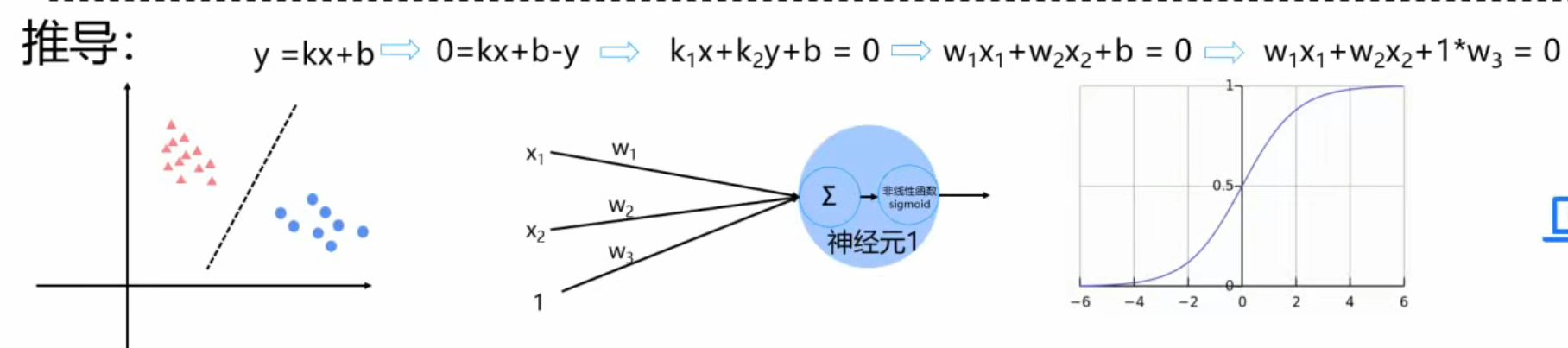
这里我们引入多个神经元，如下
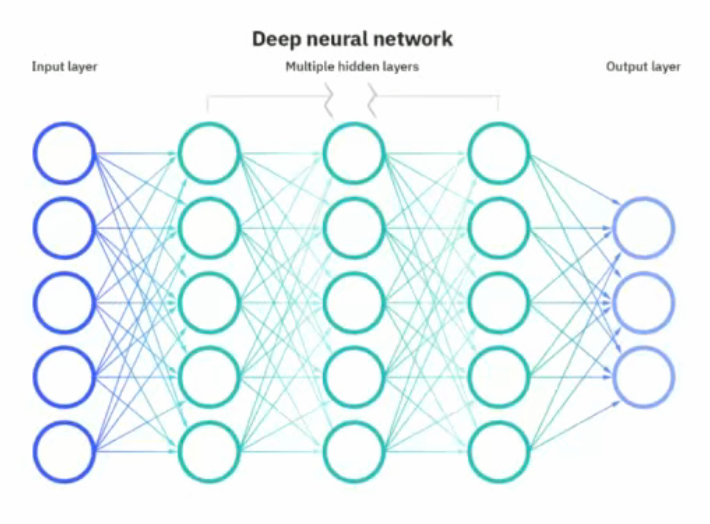
这样我们就对一个数据进行了多次非线性的变换了，所以我们得到我们想要的图像了。
数学计算
像上面这样的两层神经网络，叫做感知器，因为只对数据做了一次非线性变换，所以只能进行线性的划分。
神经网络的本质
通过参数与激活函数来拟合特征与目标之间的真实函数关系。但在一个神经网络的程序中，不需要神经元和线，本质上是矩阵的运算，实现一个神经网络最需要的是线性代数库。
偏置项
其实神经网络中，输入节点都是有一个偏置项的，只是我们不会画出来，但我们要知道
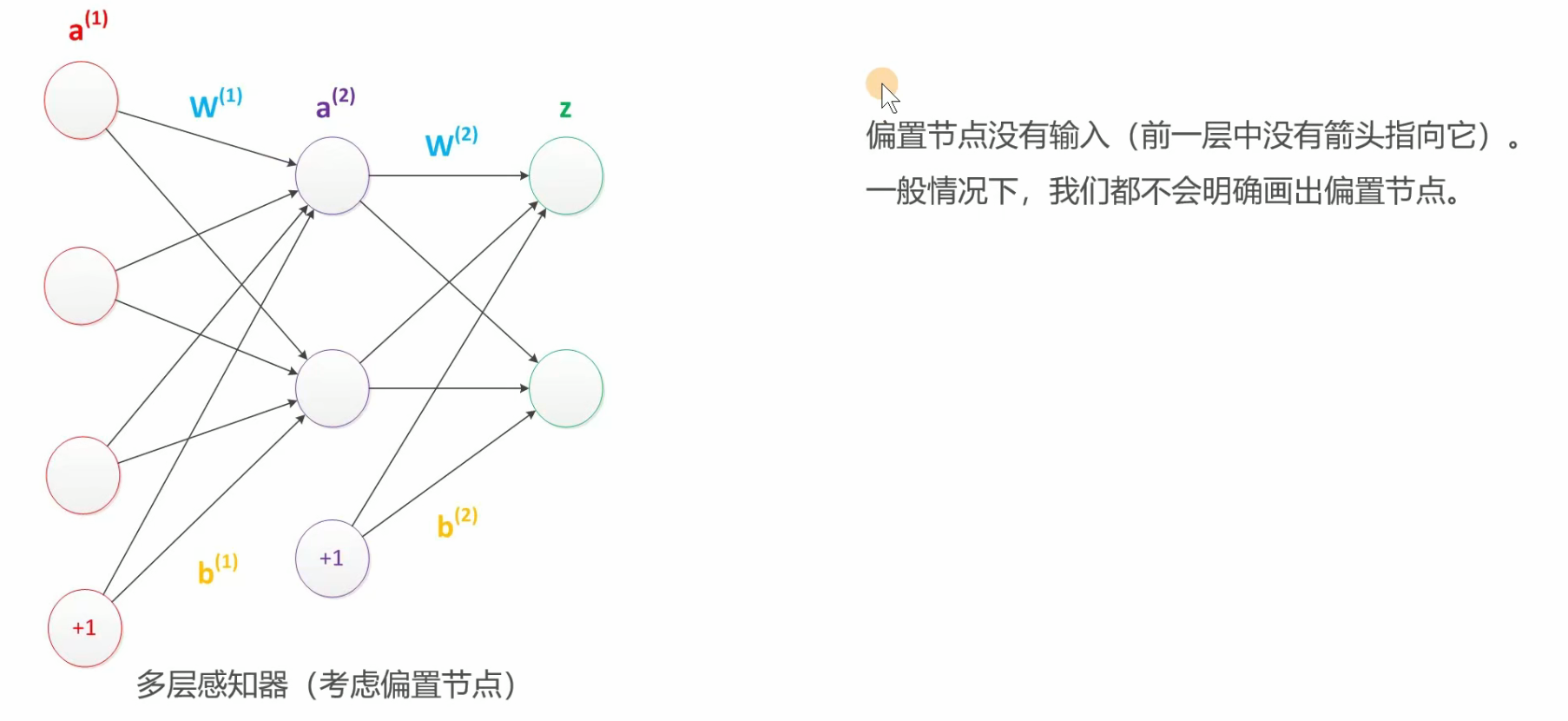
中间层的确定
输入层的节点数：与特征的维度匹配
输出层的节点数：与目标的维度匹配。
中间层的节点数：目前业界没有完善的理论来指导这个决策。一般是根据经验来设置。较好的方法就是预先设定几个可选值，通过这几个值来看整个模型的预测效果，选择效果最好的值作为最终选择。
损失函数
常用的损失函数：
0-1损失函数、均方差损失、平均绝对差损失、交叉熵损失、合页损失
神经网络既可以进行分类又可以进行回归预测，那么我们在进行分类和回归该怎么选这损失函数呢？
回归预测
回归问题是用均方差损失函数来进行衡量的，因为这个可以更好的衡量预测值和真实值之间的损失值
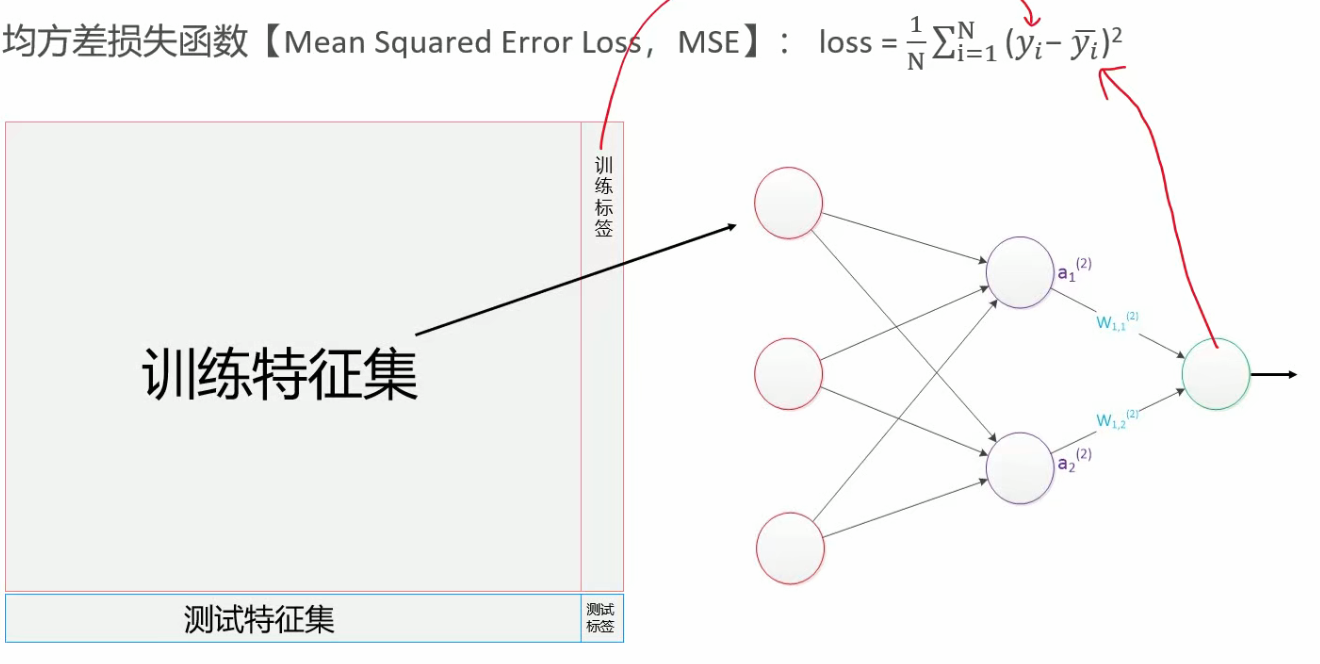
分类预测
分类预测是要用交叉熵损失函数
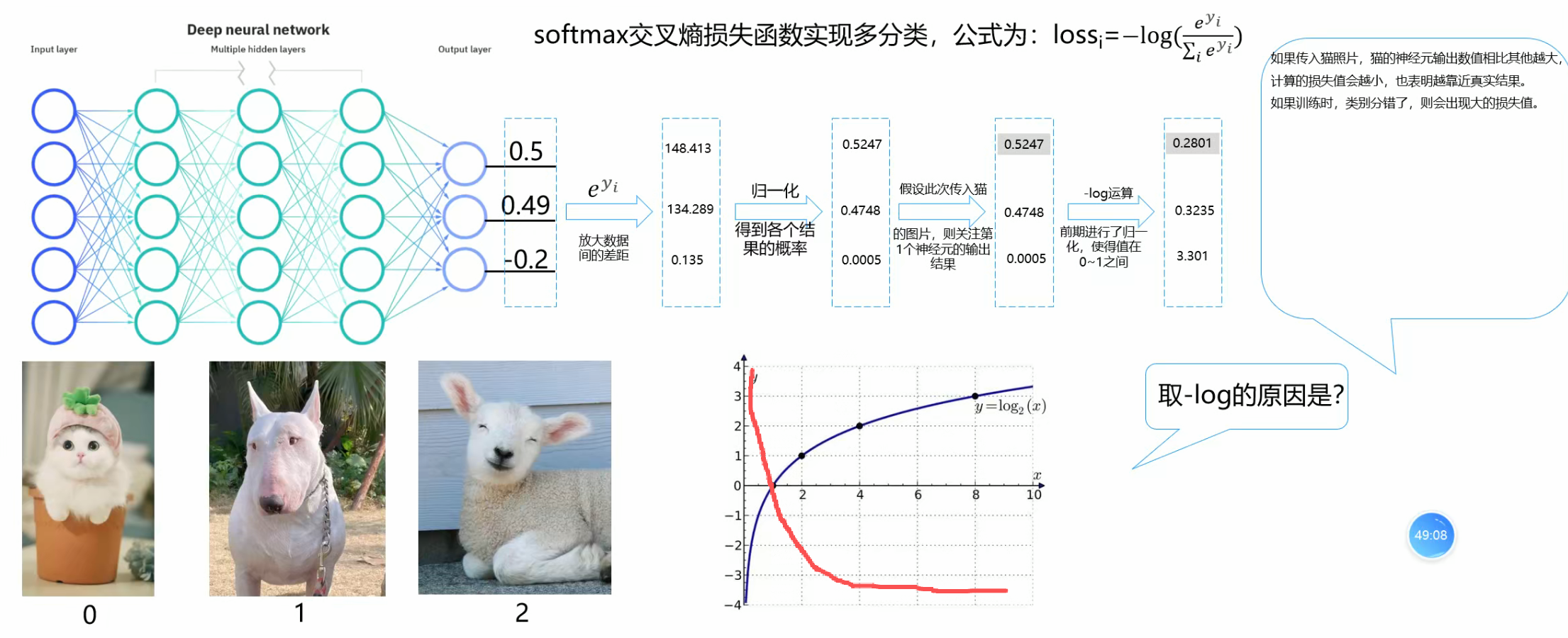如上，我们经过多层感知器得到三个值，如果这个图片是0号图片，我们就关注第一个值，可以忽略其他值，对于这个值，我们想的肯定是越大越好，然后其他值肯定是越小越好，所以我们就先指数扩大这样就可以扩大差距了那么就更明显了，归一化，进行-log运算，至于为什么要进行-log运算，具体可以看-log的图像，就是对于值越大的映射出的就越小，如果为1那么映射的就是0，这也就符合我们的预期了，我们可以把这个看成损失值。
深度学习框架介绍
我先简述一下大致框架
输入层导入数据，先随机给一组w权值和b偏置，然后一层一层进行计算计算到最后一层输出层，前面这段叫做前向传播，对输出层进行均方差损失（回归）或者交叉熵损失（分类）计算，然后进行梯度下降，然后从后向前进行w权重的调整，这些叫做反向传播。
详细版
1. 前向传播（Forward Propagation）
1.1 数据输入与初始化
神经网络的计算从输入层（Input Layer） 开始，输入数据（如图像像素、文本特征等）被传入网络。在训练之前，我们需要为每一层的权重（w） 和偏置（b） 随机初始化一组值。这些初始值通常是较小的随机数（如高斯分布或均匀分布），目的是打破对称性，避免所有神经元学习相同的特征。
1.2 逐层计算（线性变换 + 激活函数）
数据从输入层开始，逐层向前计算，直到输出层（Output Layer）。每一层的计算分为两个步骤：
(1) 线性变换（Linear Transformation）
对于第 l 层的某个神经元，其输入是上一层的输出 a^{[l-1]}，计算方式如下：
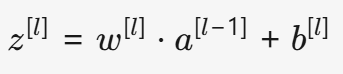
w^{[l]}：当前层的权重矩阵（形状取决于输入和神经元的数量）。b^{[l]}：当前层的偏置向量（通常每个神经元一个偏置）。z^{[l]}：线性变换后的结果（未激活的原始输出）。
(2) 激活函数（Activation Function）
线性变换后的 z^{[l]} 通常不能直接用于计算（因为线性组合无法学习复杂模式），因此需要通过非线性激活函数进行转换：
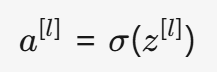
- 常见的激活函数：
- ReLU（Rectified Linear Unit） ：
a = max(0, z)（适用于隐藏层，计算高效）。 - Sigmoid ：
a = 1 / (1 + e^{-z})（适用于二分类输出层）。 - Softmax ：
a_i = e^{z_i} / \sum_j e^{z_j}（适用于多分类输出层）。
- ReLU（Rectified Linear Unit） ：
这样，数据经过线性变换 + 激活函数 后，逐层传递，最终到达输出层 ，得到模型的预测结果 y_pred。
2. 损失计算（Loss Calculation）
2.1 回归任务：均方差损失（MSE）
如果任务是回归（预测连续值，如房价、温度） ，我们使用均方误差（Mean Squared Error, MSE） 计算预测值 y_pred 和真实值 y_true 的差异：
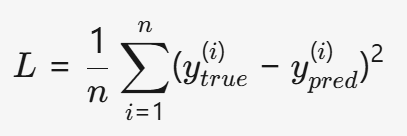
- 特点：对异常值敏感（因为平方放大了大误差的影响）。
2.2 分类任务：交叉熵损失（Cross-Entropy）
如果任务是分类（如图像识别、文本分类） ，我们使用交叉熵损失（Cross-Entropy Loss）衡量预测概率分布与真实分布的差异：
- 二分类（Sigmoid 输出） ：
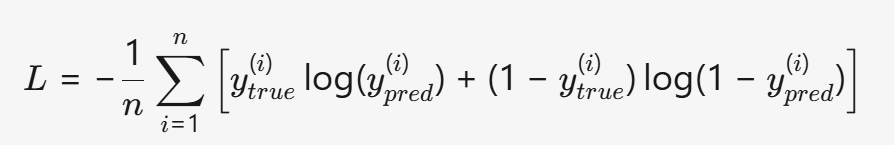
- 多分类（Softmax 输出） ：
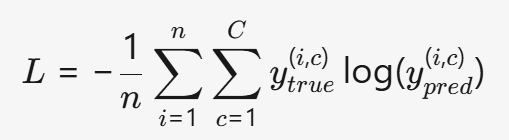
（C 是类别数，y_{true}^{(i,c)} 是真实标签的 one-hot 编码）
为什么分类用交叉熵？
- 交叉熵对错误预测惩罚更大，能更快引导模型调整参数。
- 如果用 MSE 训练分类任务，梯度会变得很小（接近 0），导致训练变慢（称为 "梯度消失"）。
3. 反向传播（Backward Propagation）
前向传播计算了预测值，损失函数衡量了预测与真实值的差距，接下来就是调整参数（w 和 b） ，使得损失最小化。这个过程就是反向传播 ，其核心是 梯度下降（Gradient Descent）。
3.1 梯度下降（Gradient Descent）
梯度下降是一种优化算法 ，其目标是找到损失函数的最小值。基本思想是：
沿着损失函数的负梯度方向，逐步调整参数，使损失减小。
数学表达式：
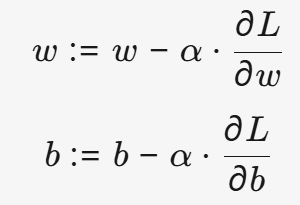
α（学习率，Learning Rate）：控制每次更新的步长（太大可能震荡，太小收敛慢）。∂L/∂w和∂L/∂b：损失函数对权重和偏置的梯度（表示参数变化对损失的影响）。
3.2 反向传播计算梯度
梯度下降需要计算 损失对每个参数的偏导数 ，但直接计算很困难。反向传播利用链式法则（Chain Rule） ，从输出层向输入层逐层计算梯度：
- 计算输出层的梯度（如交叉熵 + Softmax 的梯度计算较简单）。
- 逐层回传梯度 （利用链式法则计算
∂L/∂w和∂L/∂b）。 - 更新参数 （
w := w - α * ∂L/∂w，b := b - α * ∂L/∂b）。
关键点：
- 反向传播的核心是 链式法则，确保梯度能正确回传。
- 梯度下降的 学习率（α） 非常重要，影响训练速度和稳定性。
4. 完整流程总结（流程图）
开始
│
↓
【1. 初始化】随机初始化权重 w 和偏置 b
│
↓
【2. 前向传播】
│ ├── 输入数据 → 输入层
│ ├── 逐层计算（线性变换 z = w·a + b + 激活函数 a = σ(z)）
│ └── 输出层 → 得到预测值 y_pred
│
↓
【3. 损失计算】
│ ├── 回归任务 → 均方误差（MSE）
│ └── 分类任务 → 交叉熵损失（Cross-Entropy）
│
↓
【4. 反向传播】
│ ├── 计算损失对 w 和 b 的梯度（链式法则）
│ ├── 使用梯度下降更新参数（w := w - α * ∂L/∂w）
│ └── 逐层回传梯度（从输出层 → 输入层）
│
↓
【5. 迭代训练】重复前向传播 → 损失计算 → 反向传播，直到损失足够小
│
↓
结束（模型训练完成）5. 总结
- 前向传播：数据从输入层逐层计算，经过线性变换和激活函数，最终得到预测值。
- 损失计算：用 MSE（回归）或交叉熵（分类）衡量预测与真实值的差距。
- 反向传播 ：利用链式法则计算梯度，并通过梯度下降调整
w和b，使损失最小化。 - 迭代优化：重复上述过程，直到模型收敛（损失足够小）。
神经网络的核心就是 "前向计算预测 → 计算误差 → 反向调整参数" 的循环过程，而梯度下降则是优化参数的关键工具。理解这一框架，是掌握深度学习的基础！ 🚀