大家好,今天咱们聊聊时间序列异常检测这个实用技术,它在金融风控、工业设备监控等领域应用广泛。
很多人觉得这个话题复杂,其实只要掌握核心方法,就能轻松上手。
本文将介绍两种经典技术------隐马尔可夫模型(HMM)和长短时记忆网络(LSTM),并通过代码示例展示实际应用。文章最后,我还分享了一门配套课程视频,帮你巩固学习。
一、隐马尔可夫模型(HMM)在异常检测中的应用
HMM是一种统计模型,特别适合处理隐藏状态变化的数据。简单说,它假设系统有一系列我们看不见的状态(比如设备运行模式),这些状态按概率转移,而我们只能观测到相关输出(如传感器读数)。HMM的核心包括三部分:
-
状态转移概率矩阵A:描述状态间切换的概率,比如从状态i转到j的概率。
-
发射概率B:表示在某个状态下观测到特定输出的概率。
-
初始状态分布π:系统起点的状态概率。
在异常检测中,我们先用正常数据训练HMM模型,获得参数λ = {A, B, π}。然后,对新数据计算其生成概率P(O|λ)。如果这个概率远低于正常水平,就判定为异常。这背后的逻辑很直观:异常数据不符合模型学到的"正常"模式。
关键算法是前向算法,高效计算概率:初始化α₁(j),递归更新αₜ(j),最后求和得P(O|λ)。Viterbi算法也能辅助,用于找最可能的状态序列。
二、长短时记忆网络(LSTM)在异常检测中的应用
LSTM是一种循环神经网络,专为时序数据设计。它通过门控机制(如输入门、遗忘门)解决长距离依赖问题,能捕捉复杂的时间模式。LSTM的核心结构包括:
-
输入门:控制新信息流入。
-
遗忘门:决定保留多少旧记忆。
-
输出门:生成当前输出。
-
细胞状态更新:结合新旧信息。
在异常检测中,LSTM常用作预测模型或自编码器。例如:
-
预测模型:训练LSTM预测下一时间点数据,计算预测误差Eₜ = ‖xₜ - x̂ₜ‖²。误差超过阈值就是异常。
-
自编码器:让模型重构输入数据,用重构误差E = (1/T)∑‖xₜ - x̂ₜ‖²检测异常。误差大说明数据偏离正常模式。
三、完整案例:实战对比HMM和LSTM
咱们用一个虚拟数据集演示。数据包含周期性波动和随机异常点,生成代码如下:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
np.random.seed(42)
time = np.arange(0, 1000)
data_normal = np.sin(0.02 * time) + np.random.normal(0, 0.1, size=time.shape)
data = data_normal.copy()
anomaly_indices = np.random.choice(time, size=20, replace=False)
data[anomaly_indices] += np.random.choice([3, -3], size=20)
plt.figure(figsize=(12, 4))
plt.plot(time, data, color='royalblue', label='原始数据')
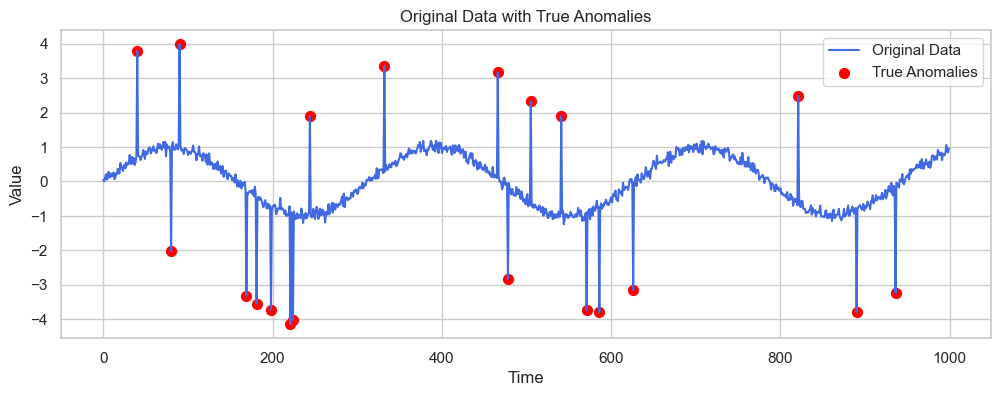
plt.scatter(anomaly_indices, data[anomaly_indices], color='red', s=50, label='真实异常点')
plt.legend()
plt.show()生成的数据可视化如下(蓝色曲线是正常波动,红点是插入的异常):
HMM实现:
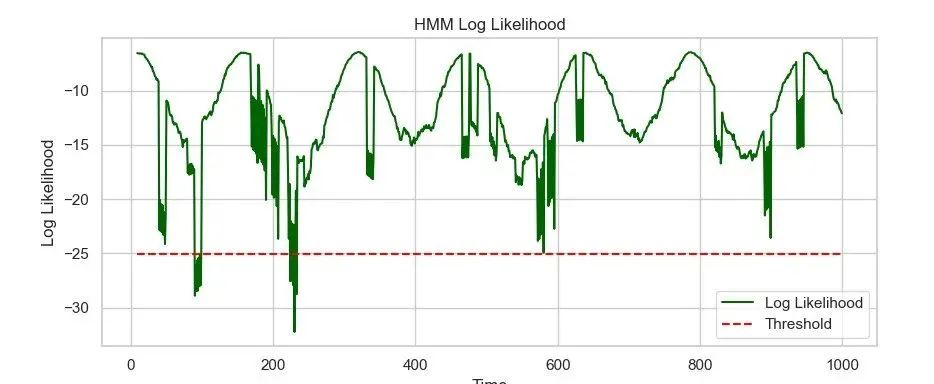
用hmmlearn库训练GaussianHMM模型,滑动窗口计算对数似然。概率低于阈值(如均值减3倍标准差)即判为异常。
from hmmlearn import hmm
model_hmm = hmm.GaussianHMM(n_components=3, covariance_type="diag", n_iter=100)
model_hmm.fit(X)
log_likelihoods = [model_hmm.score(window) for window in sliding_windows]
threshold_hmm = np.mean(log_likelihoods) - 3 * np.std(log_likelihoods)LSTM实现:
用PyTorch构建自编码器,计算重构误差。误差超过阈值(如均值加3倍标准差)为异常。
import torch
import torch.nn as nn
model = LSTMAutoencoder(sequence_length=20, n_features=1).to('cuda')
# 训练代码省略,重点在重构误差
reconstruction_errors = torch.mean((X_seq_tensor - model(X_seq_tensor))**2, dim=(1,2))
threshold_lstm = np.mean(reconstruction_errors) + 3 * np.std(reconstruction_errors)结果可视化对比:HMM基于概率(绿色曲线),LSTM基于误差(紫色曲线),两者都能有效检测异常。
四、方法对比与实用建议
| 方法 | 优势 | 局限 | 适用场景 |
|---|---|---|---|
| HMM | 概率解释性强,模型直观 | 高维数据适应性弱 | 状态转移明显的系统,如设备故障检测 |
| LSTM | 非线性建模强,适合复杂时序 | 需大量数据,解释性差 | 金融波动或网络流量分析 |
实际应用中,可以结合两者:用HMM处理状态变化,LSTM处理复杂模式,融合结果提高准确率。时间序列异常检测的关键是理解数据本质和业务场景,而不是盲目堆砌算法。
五、学习推荐
这篇文章带大家走了一遍HMM和LSTM的实战流程。
如果想更系统学习时间序列分析,比如深入理解模型原理或扩展应用,我推荐一门课程视频:https://pan.quark.cn/s/6a2a49ff0285
它涵盖核心概念和案例,适合巩固知识。
希望本文对你有帮助!