作为新手入门，推荐鱼书，本篇做一个简单的目录知识点总结，咸鱼可买本书电子书，内容相对简单易懂，同时大家可以在github上搜相关的配套代码，推荐编辑器vscode
《深度学习入门：基于Python的理论与实现》章节知识总结
第1章 Python入门
-
Python基础：介绍Python的安装（推荐Anaconda发行版）、版本选择（Python 3.x）、解释器使用（算术计算、数据类型、变量、列表、字典、布尔型、条件语句、循环语句、函数、类），以及Python脚本文件的编写与运行。
-
NumPy库：深度学习数值计算核心工具，包括数组生成、算术运算（元素级运算、广播机制）、N维数组操作（形状查看、矩阵乘法）、元素访问（索引、切片）。
-
Matplotlib库：数据可视化工具，讲解如何绘制简单图形（如sin/cos曲线）、设置图表标签与标题，以及显示图像数据（如MNIST手写数字）。
第2章 感知机
神经网络的"前身"，理解深度学习的基础单元与线性/非线性表示的核心矛盾。
- 感知机原理：接收多个输入信号，通过权重（控制信号重要性）和偏置（调整激活难度）计算加权和，再通过阶跃函数（激活函数）输出0或1，数学表达式为：
-
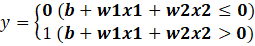
逻辑电路实现：用感知机实现与门、与非门、或门（仅需调整权重和偏置），但无法实现异或门------暴露感知机的核心局限性：只能表示线性可分空间（用直线分割数据）。
-
多层感知机：通过叠加层（如"与非门+或门+与门"组合）实现异或门，证明：多层结构可表示非线性空间（用曲线分割数据），为神经网络的分层结构提供理论基础。
理解"分层"是突破线性局限的关键，为后续神经网络的层级结构铺垫；感知机的权重/偏置概念，直接对应神经网络的核心参数。
第3章 神经网络
从感知机过渡到神经网络，掌握神经网络的前向传播（推理）流程与核心组件。
- 神经网络结构：输入层、隐藏层、输出层的层级划分，通过激活函数（替代感知机的阶跃函数）实现信号的连续变换，核心公式为：
a *=b+w1x1+w2x2, y=h(a)*其中h(·)为激活函数。
-
激活函数：对比阶跃函数（不连续）、sigmoid函数（平滑连续，适合分类）、ReLU函数（ReLU(x)=max(0,x)，缓解梯度消失，当前主流），激活函数必须是非线性的（否则多层网络等价于单层）。
-
多维数组运算：用NumPy实现矩阵乘法（神经网络的核心运算），确保输入与权重的维度匹配，如输入X(2,)与权重W(2,3)相乘，输出Y(3,)。
-
3层神经网络实现：输入层（784个神经元，对应MNIST图像28×28）→ 隐藏层（含激活函数）→ 输出层（10个神经元，对应0-9分类），输出层激活函数根据任务选择：回归用恒等函数，分类用softmax函数（将输出归一化为概率）。
掌握神经网络的前向传播逻辑，理解激活函数、矩阵运算、批处理的作用，能独立实现简单的图像分类推理。
第4章 神经网络的学习
神经网络的"训练"核心，掌握损失函数、梯度下降法，实现参数（权重、偏置）的自动更新。
-
数据划分：训练数据（用于学习参数）与测试数据（评估泛化能力），避免过拟合（仅拟合训练数据，不适应新数据）。
-
损失函数：衡量模型输出与真实标签的差距，常用两种：
均方误差（适合回归）：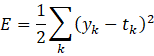
（
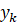为模型输出，
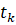为真实标签）；
交叉熵误差（适合分类）：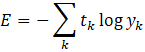
（仅关注正确标签对应的输出，对错误预测惩罚更明显）。
- 数值微分：通过微小差分近似计算导数（梯度），公式为：
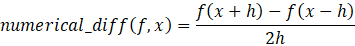
缺点是计算耗时，但实现简单，可用于验证梯度正确性（梯度确认）。
- 梯度下降法：沿梯度（损失函数对参数的偏导数向量）方向更新参数，最小化损失函数，参数更新公式为：
W←W−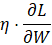
其中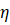
为学习率（超参数，控制更新步长），批量梯度下降（用全部数据）或随机梯度下降（SGD，用mini-batch数据）。
- 2层神经网络训练：实现"mini-batch采样→计算梯度→更新参数"的循环，训练MNIST数据集，观察损失函数下降与精度提升。
掌握神经网络学习的核心逻辑：以损失函数为目标，用梯度下降法自动优化参数；理解超参数（如学习率）对训练效果的影响。
第5章 误差反向传播法
替代数值微分的高效梯度计算方法，大幅提升神经网络训练速度。
-
计算图：将计算过程拆分为节点（如"+""×""exp"）和边，通过"正向传播"计算结果，"反向传播"计算梯度（基于链式法则），核心思想是"局部计算"（每个节点仅需关注自身的梯度传递）。
-
链式法则：复合函数的导数等于各函数导数的乘积，如z=f(t), t=g(x)，则
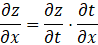，是反向传播的数学基础。 -
简单层实现：将神经网络的组件封装为"层"，每个层含forward（正向传播）和backward（反向传播）方法：
-
加法层：反向传播时将上游梯度原封不动传递给下游；
-
乘法层：反向传播时传递"上游梯度×另一输入"（输入翻转）；
-
ReLU层：正向传播记录输入是否≤0（mask），反向传播时将mask处梯度设为0；
-
Sigmoid层：利用数学简化，反向传播仅需正向输出 y，公式为
-
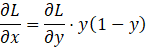
Affine层：本质是全连接，实现矩阵乘法+偏置，反向传播计算权重、偏置、输入的梯度；
-
Softmax-with-Loss层：结合softmax（输出概率）和交叉熵误差（计算损失），反向传播直接输出 y-t（模型输出与真实标签的差分），简化计算。
- 误差反向传播法实现：组装各层为神经网络，通过正向传播计算损失，反向传播计算所有参数的梯度，效率远高于数值微分（如MNIST训练时间从小时级缩短到分钟级）。
第6章 与学习相关的技巧
优化神经网络训练的实用技术，提升收敛速度、抑制过拟合、优化超参数。
-
参数更新方法：对比SGD（简单但易陷入局部最优）、Momentum（模拟动量，加速收敛）、AdaGrad（自适应学习率，适合稀疏数据）、Adam（融合Momentum和AdaGrad，当前主流），通过实验验证Adam等方法收敛更快。
-
权重初始值：
-
不能设为0（导致权重对称更新）；
-
激活函数为sigmoid/tanh时用Xavier初始值（
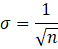，n 为前一层节点数）； -
激活函数为ReLU时用He初始值（
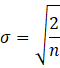），避免梯度消失或梯度爆炸。
-
Batch Normalization（批归一化）：对每批数据的激活值进行"均值0、方差1"的归一化，（再通过参数γ（缩放）和β（平移）调整，优点：加速训练、降低初始值敏感度、抑制过拟合。）
-
正则化：抑制过拟合的核心技术：
-
权值衰减（L2正则化）：损失函数加
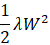，惩罚大权重； -
Dropout：训练时随机"关闭"部分神经元（如50%概率），测试时将输出乘以保留概率，模拟集成学习。
- 超参数优化：用验证数据（从训练数据拆分，如20%）评估超参数，通过"随机采样→缩小范围"的循环优化（避免网格搜索的低效），超参数如学习率（1e-6~1e-2）、权值衰减系数（1e-8~1e-4）。
掌握深度学习工程化的关键技巧，解决"训练慢、过拟合、超参数难调"等实际问题，提升模型性能与稳定性。
第7章 卷积神经网络（CNN）
专为图像识别设计的神经网络，利用卷积、池化提取图像的空间特征，大幅提升图像分类精度。
-
CNN结构：与全连接网络的核心区别是新增"卷积层"（提取局部特征）和"池化层"（缩小空间尺寸），典型结构为"Conv→ReLU→(Pool)→Conv→ReLU→(Pool)→Affine→Softmax"。
-
卷积层：
- 卷积运算：用滤波器（权重）在输入图像上滑动（步幅stride），计算局部加权和，通过填充（pad）控制输出尺寸，公式为：
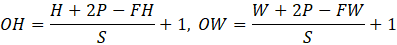
（H/W为输入尺寸，FH/FW为滤波器尺寸，P为填充，S为步幅）；
- 多通道处理：输入含C个通道时，滤波器也需C个通道，输出为单通道（各通道结果求和）；多个滤波器可输出多通道特征图；
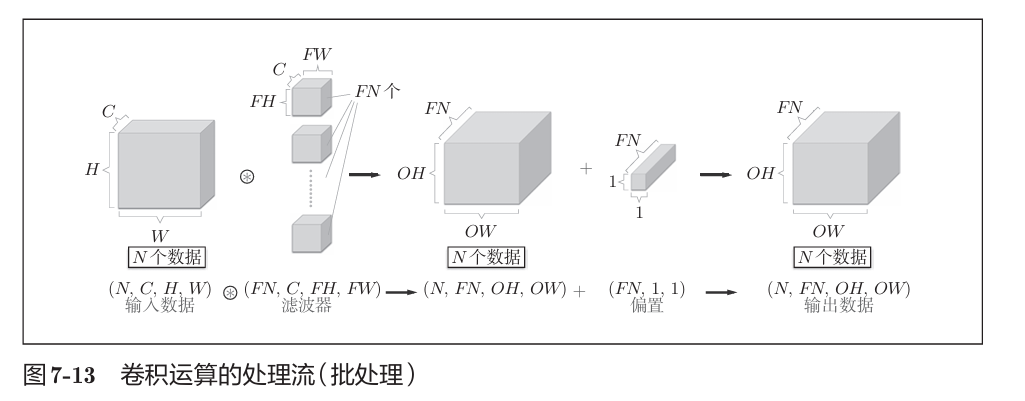
- 实现技巧：用im2col函数将卷积运算展开为矩阵乘法，简化计算并利用NumPy的高效矩阵运算。
- 池化层：
-
作用：缩小空间尺寸（如2×2 Max池化，步幅2）、降低过拟合（保留关键特征，丢弃冗余信息）、对微小位置变化鲁棒；
-
特点：无学习参数，通道数不变，常用Max池化（取局部最大值）。
-
CNN实现：搭建"Conv→ReLU→Pool→Affine→ReLU→Affine→Softmax"的CNN，训练MNIST数据集，识别精度达98.96%；通过可视化卷积层权重，发现浅层滤波器提取边缘、斑块等低级特征，深层提取更抽象的高级特征。
-
经典CNN：LeNet（1998年，CNN鼻祖，用sigmoid和子采样）、AlexNet（2012年，深度学习热潮导火索，用ReLU、LRN、Dropout，GPU加速）。
第8章 深度学习
-
加深网络：搭建更深的CNN（如6个卷积层+2个全连接层），用3×3小型滤波器、ReLU、He初始值、Adam、Dropout等技术，MNIST识别精度达99.38%，错误案例多为人类也难判断的模糊图像。
-
深度学习小历史：回顾ImageNet竞赛推动的网络演进：VGG（堆叠3×3卷积层，加深网络）、GoogLeNet（引入Inception模块，提高参数效率）、ResNet（引入残差连接，解决深层网络梯度消失问题）。
-
深度学习高速化：GPU加速（并行计算矩阵运算）、分布式学习（多GPU/多机器）、低精度运算（如FP16替代FP32，减少计算量）。
-
应用案例：物体检测（如Faster R-CNN）、图像分割（如FCN）、图像标题生成（结合CNN与RNN）、自动驾驶、强化学习（Deep Q-Network）。
-
未来方向：图像风格迁移、图像生成（GAN）、自动驾驶、强化学习等，强调深度学习的端到端学习（从原始数据直接输出结果）优势。