6.1 Other dimensionality reduction methods
6.2 SRM view of PCA
6.3 OLSR
6.4 OLSR to SVR
6.5 Hurricane Intensity Regression
6.1 其他降维方法
6.2 PCA 的 SRM 视图
6.3 OLSR
6.4 OLSR 到 SVR
6.5 飓风强度回归
Regression 回归
- [1 Regression 回归](#1 Regression 回归)
- [2 普通最小二乘回归(Ordinary Least Squares Regression, OLSR)](#2 普通最小二乘回归(Ordinary Least Squares Regression, OLSR))
-
- [2.1 模型表示 (Representation)](#2.1 模型表示 (Representation))
- [2.2 评价准则 (Evaluation)](#2.2 评价准则 (Evaluation))
- [2.3 优化问题 (Optimization Problem)](#2.3 优化问题 (Optimization Problem))
- [2.4 闭式解 (Closed Form Solution)](#2.4 闭式解 (Closed Form Solution))
- [2.5 图像说明 (Intuition)](#2.5 图像说明 (Intuition))
- [2.6 简单例子](#2.6 简单例子)
- [3 普通最小二乘回归 (OLS) vs 支持向量回归 (SVR)](#3 普通最小二乘回归 (OLS) vs 支持向量回归 (SVR))
-
- [3.1 OLS 的损失函数](#3.1 OLS 的损失函数)
- [3.2 SVR 的不同点](#3.2 SVR 的不同点)
- [3.3 总结对比表](#3.3 总结对比表)
- [4 支持向量回归 (Support Vector Regression, SVR)](#4 支持向量回归 (Support Vector Regression, SVR))
- 回归分析的一些问题
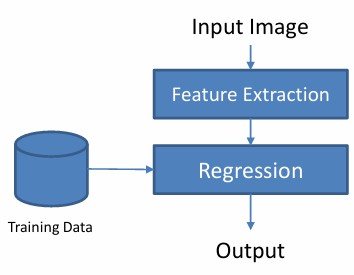
1 Regression 回归
回归是一类 监督学习方法,目标是学习一个函数 f ( x ) f(x) f(x) 使得输入 x x x 能预测输出 y y y。
f ( x ) ≈ y f(x)≈y f(x)≈y
x x x:自变量(输入)
y y y:因变量(输出)
≈ ≈ ≈:意味着预测值和真实值尽可能接近
换句话说,回归就是在寻找输入和输出之间的关系。
输出为连续变量
示例:根据图像预测年龄

数学形式
用于 -- 预测和预报 -- 评估变量之间的相互影响
数学公式
x x x 是由特征组成
y y y 是我们要求的感兴趣的变量
x , y x,y x,y 都可以是多维的
模型(Model):
y = f ( x ; w ) + ϵ y = f(x; w) + \epsilon y=f(x;w)+ϵ
例如(For example): y = w x + b + ϵ y = wx + b + \epsilon y=wx+b+ϵ
目标(Objective): 估计参数 w w w,使得模型输出尽可能接近给定的目标值。
2 普通最小二乘回归(Ordinary Least Squares Regression, OLSR)
2.1 模型表示 (Representation)
回归模型形式为:
f ( x ) = w T x + b f(x) = w^T x + b f(x)=wTx+b
其中:
- x x x: 输入特征向量
- w w w: 权重参数,所求
- b b b: 偏置项
2.2 评价准则 (Evaluation)
正则化 :无
误差函数 :平方损失 (Square Loss)
l ( f ( x ) , y ) = ( f ( x ) − y ) 2 l(f(x), y) = (f(x) - y)^2 l(f(x),y)=(f(x)−y)2
很简单,不像SVM它们的铰链损失函数,这个就是误差平方。
2.3 优化问题 (Optimization Problem)
最小化所有样本的平方误差和:
min w ∑ i = 1 N ( w T x i − y i ) 2 \min_w \sum_{i=1}^N (w^T x_i - y_i)^2 wmini=1∑N(wTxi−yi)2
矩阵形式:
∥ X w − y ∥ 2 = ( X w − y ) T ( X w − y ) \|Xw - y\|^2 = (Xw - y)^T (Xw - y) ∥Xw−y∥2=(Xw−y)T(Xw−y)
2.4 闭式解 (Closed Form Solution)
对 w w w 求导并令其为 0,得到解析解:
w = ( X T X ) − 1 X T y w = (X^T X)^{-1} X^T y w=(XTX)−1XTy
很容易求解,甚至不用用到梯度下降算法。
- x x x: 输入特征向量
- w w w: 权重参数,所求
2.5 图像说明 (Intuition)
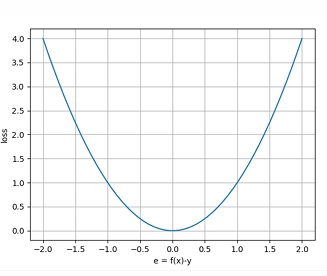
损失函数是一个 凸函数(碗状二次曲线),叫平方损失,保证唯一最优解。 最小点对应于平方误差的最小值,即闭式解。
问题: 如果我们更改这个损失函数,比如由二次方变成四次方。这条线或者 w w w 之间会有所不同吗?
我们这个算法对异常值非常敏感,减少它的一种方式就是摆脱平方。但,当我们摆脱平方,我们很容易找到 w w w的值。但这样做,绝对总和不能够分析性的解决,需要用梯度下降算法。所以,如果我们摆脱了一件事,但会收获计算复杂性。
2.6 简单例子
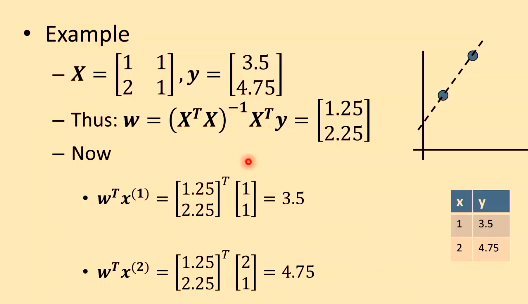
3 普通最小二乘回归 (OLS) vs 支持向量回归 (SVR)
3.1 OLS 的损失函数
普通最小二乘回归 (OLS) 使用的是 平方损失 (Square Loss):
L ( y , y ^ ) = ( y − y ^ ) 2 L(y, \hat{y}) = (y - \hat{y})^2 L(y,y^)=(y−y^)2
问题:
- 对离群点 (outliers) 非常敏感
- 因为误差会被 平方放大
3.2 SVR 的不同点
支持向量回归 (SVR) 的核心区别在于 损失函数。
将平方损失换成 绝对值损失 (Absolute Loss):
L ( y , y ^ ) = ∣ y − y ^ ∣ L(y, \hat{y}) = |y - \hat{y}| L(y,y^)=∣y−y^∣
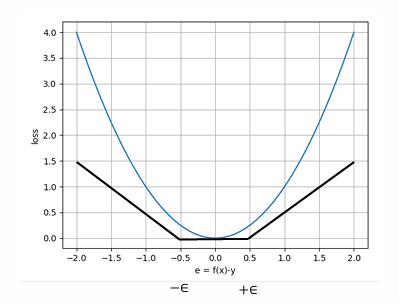
或者使用 ϵ \epsilon ϵ-不敏感损失 (Epsilon-insensitive Loss):
L ( y , y ^ ) = { 0 , ∣ y − y ^ ∣ ≤ ϵ ∣ y − y ^ ∣ − ϵ , otherwise L(y, \hat{y}) = \begin{cases} 0, & |y - \hat{y}| \leq \epsilon \\ |y - \hat{y}| - \epsilon, & \text{otherwise} \end{cases} L(y,y^)={0,∣y−y^∣−ϵ,∣y−y^∣≤ϵotherwise
这样可以减轻对离群点的敏感性,更加稳健。
3.3 总结对比表
| 方法 | 损失函数 | 对离群点敏感性 | 特点 |
|---|---|---|---|
| OLS | 平方损失 ( y − y ^ ) 2 (y - \hat{y})^2 (y−y^)2 | 很敏感 | 最小化方差,解析解简单 |
| SVR | 绝对值损失 或 ϵ \epsilon ϵ-不敏感损失 | 鲁棒性更好 | 抗噪声能力强,对离群点不敏感 |
一句话总结
- OLS → 用平方损失,对离群点非常敏感
- SVR → 损失函数换成绝对值 / ϵ \epsilon ϵ-不敏感形式,对离群点更鲁棒。对异常值更加稳健
4 支持向量回归 (Support Vector Regression, SVR)
除了损失函数,和OLS没有区别
模型表示 (Representation)
f ( x ) = w T x + b f(x) = w^T x + b f(x)=wTx+b
评价准则 (Evaluation)
正则化项 :
w T w w^T w wTw
用于控制模型复杂度
误差项 :
使用 ε-不敏感损失函数
l ( f ( x ) , y ) = max ( 0 , ∣ f ( x ) − y ∣ − ϵ ) l(f(x), y) = \max(0, |f(x) - y| - \epsilon) l(f(x),y)=max(0,∣f(x)−y∣−ϵ)
- 当预测值和真实值的差距小于 ϵ \epsilon ϵ 时,损失为 0
- 当差距超过 ϵ \epsilon ϵ 时,才会产生损失
- 这样可以减少模型对小误差和噪声的敏感性
优化问题 (Optimization Problem)
SVR 的目标函数为:
min w , b 1 2 w T w + C N ∑ i = 1 N max ( 0 , ∣ f ( x i ) − y i ∣ − ϵ ) \min_{w, b} \ \frac{1}{2} w^T w + \frac{C}{N} \sum_{i=1}^N \max \big(0, |f(x_i) - y_i| - \epsilon \big) w,bmin 21wTw+NCi=1∑Nmax(0,∣f(xi)−yi∣−ϵ)
对其的优化,我们会使用梯度下降算法。
- w w w:权重向量
- b b b:偏置
- C C C:惩罚系数(平衡正则化和误差项)
- N N N:样本数
回归分析的一些问题
如果两个变量不相关 (unrelated) ,那么它们的回归系数应该接近 0,即一个变量对另一个变量没有线性解释能力。
如果两个变量正相关 (positively related),那么回归系数应为 正数,说明自变量增加时因变量也会增加。
回归方向不同,系数是否相同?
一般情况下,不相同
比如,
y = w y x x + b y x + ϵ y x y = w_{yx}x + b_{yx} + \epsilon_{yx} y=wyxx+byx+ϵyx
x = w x y y + b x y + ϵ x y x = w_{xy}y + b_{xy} + \epsilon_{xy} x=wxyy+bxy+ϵxy
这两种回归系数通常不一样。
因为回归是有方向性的,X 回归 Y 和 Y 回归 X 的残差不同。
误差是否会与自变量相关?
在理想的线性回归假设中,误差与自变量独立。
如果误差和自变量相关,说明模型设定有问题(比如遗漏了重要变量),会导致估计偏差。