A Deep Reinforcement Learning Approach for the Meal Delivery Problem
本文将动态外卖配送建模为马尔可夫决策过程,利用深度强化学习在有限骑手条件下联合优化实时派单、智能拒单与骑手重定位,实验表明该策略在合成与真实数据上均较基线显著提升期望总奖励、缩短平均送达时间,并给出不同订单频率下的最优骑手配置与鲁棒性验证。
本文构建了一个融合拒单、多单合并与骑手重定位的 MDP 外卖模型,用八类 DQN 算法求解,在合成与真实数据上证明其可同时提升平台利润、缩短送达时间,并首次给出小时级"最优骑手数"配置方案。
感觉问题规模有点小,方法在真实场景不是很适用
研究目标
在骑手数量有限的前提下,最大化平台利润,同时:
最小化期望延迟;
允许拒接低收益/远距离订单;
动态指派多单合并配送;
给出"每时段最优骑手数量"。
方法亮点
首次提出针对外卖场景的完整 MDP 模型:
-- 状态:骑手位置、订单分布、餐厅/顾客/仓库地理信息。
-- 动作:接单/拒单、路径选择、多单合并、空驶重定位(可去热门餐厅而非直接回仓)。
-- 奖励:完成时效、利润、未来潜在收益的综合。
求解:系统比较 8 种 DQN 变体,并在合成 + 真实运营数据集上调参验证。
实验输出:
-- 不同订单量下的小时级"最优骑手数";
-- 骑手利用率热力图,揭示工作负荷分布。
建模假设
地图离散化为 500 m×500 m 网格,一步≈1 分钟。
订单到达服从指数分布,全天速率 λt 随小时波动。
餐食制备 5--15 min;平台承诺 25 min、容忍上限 45 min。
骑手完成一单后可直接去热门餐厅"预置",而非一定回仓。
多端下单被拆成多个独立订单处理。
MDP 要素
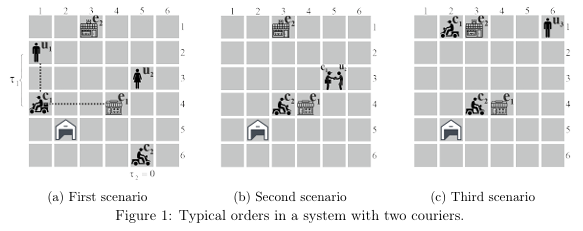
状态 S:对每一骑手 c 与订单 o,仅存
-- 期望送达时长 τoc(含取餐距离、制备、骑手当前任务余量)
-- 骑手距仓库距离 Δc
-- 骑手距各餐厅距离 Δec
动作 A:
-- 接单/拒单 xoc、xo
-- 空闲时可去某餐厅 ec 或回仓 c
奖励 r(s,a):
-- 接单:45--τoc(τoc≤45)
-- 拒单:-15
-- 空驶:-10
状态-动作空间大幅缩减,便于深度网络学习。

深度 RL 算法
比较 8 种 DQN 变体:
-- 标准 DQN(Experience Replay + Target Net)
-- Double DQN(DDQN)
-- Prioritized Experience Replay(PER)
-- Dueling DDQN(D3QN)
-- 软/硬更新、超参:γ=0.9,网络 64-128-128-64,批大小 128,记忆池 20k。
基准策略
P45:超时 45 min 拒单,空闲即回仓。
P60:超时 60 min 拒单,其余同 P45。
数据集
合成:10×10 网格,7 家餐厅,仓库居中。
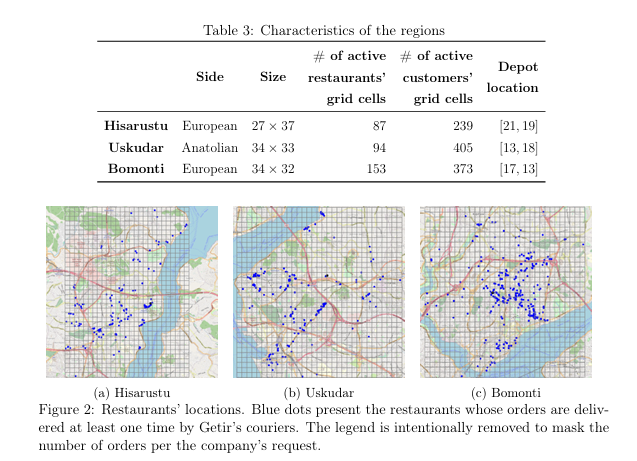
真实:Getir 伊斯坦布尔 3 区域
-- Hisarustu(低密度)
-- Üsküdar(中密度)
-- Bomonti(高密度)
→ 均已网格化(500 m),含餐厅/顾客/仓库坐标、2019.10--2020.4 订单。
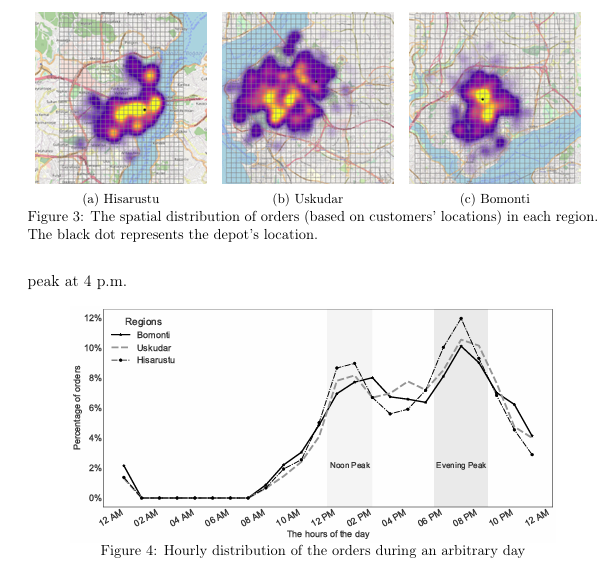
→ 全天两高峰:12--15h、17--21h,区域间峰值形态略有差异。
实验结果
算法选型
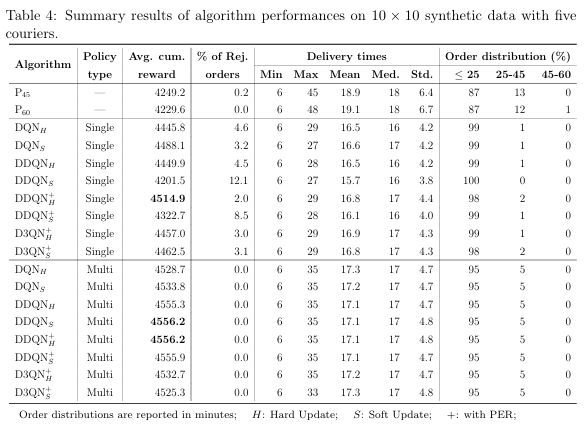
- 在合成 10×10 网格、日均 163 单、5 骑手场景下,比较 8 种 DQN 扩展(DQN/DDQN/DDQN+PER/D3QN,每种再分硬/软更新)。
- 指标:100 天测试的平均累计奖励、拒单率、配送时间。
- 结果:DDQN + PER + Hard Update(DDQN+H)综合最优,奖励最高且拒单少;所有深度算法均明显优于 P45/P60 两条规则基线。
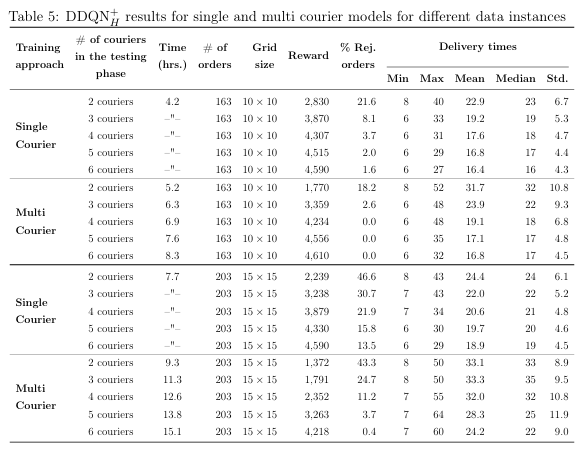
单骑手 vs 多骑手训练
- 单骑手策略训练快(≈4 h),可零成本泛化到任意数量骑手;多骑手策略需按"实际骑手数"重训(6--10 h)。
- 在骑手≤3 人时,单骑手策略奖励更高;骑手≥4 人时,多骑手策略因能捕捉骑手间交互而反超。
- 结论:后续实验采用"单骑手训练+共享策略"作为近似,兼顾效率与效果。
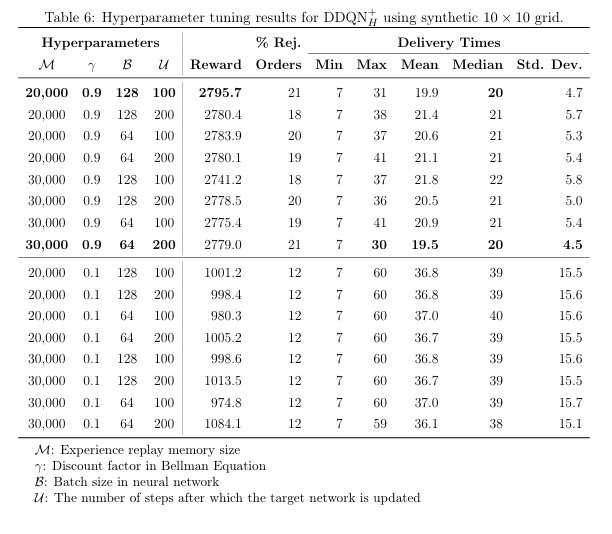
超参数调优
- 对 DDQN+H 在 16 组超参(M∈{20k,30k}, γ∈{0.9,0.1}, B∈{64,128}, U∈{100,200})中做网格搜索。
- 最优配置:M=20 k, γ=0.9, B=128, U=100(硬更新),累计奖励 2795.7;γ=0.1 导致奖励腰斩、拒单/延迟激增。
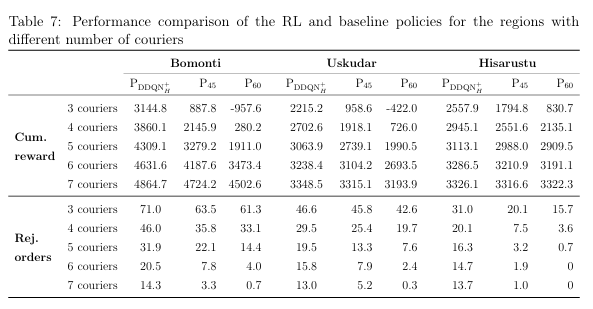
Getir 真实数据测试
- 用 DDQN+H 训练 1000 天,测试 100 天。
- 三区域日均单量:Hisarustu 141、Üsküdar 172、Bomonti 220。
- 结果
-- 奖励:DDQN+H 全面 > P45 > P60;3--4 骑手时差距最大(>3 倍)。
-- 拒单:DDQN+H 随骑手增加迅速下降,5 骑手后几乎为 0;P60 在 7 骑手仍有 0--3% 拒单。
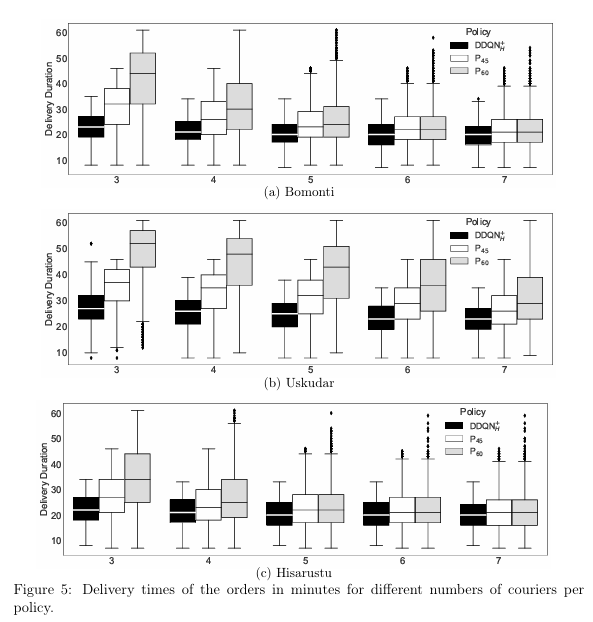
-- 配送时间:骑手≤4 人时,DDQN+H 中位数比基线缩短 5--15 min;骑手≥5 人时差距缩小。
-- 边际收益:≥5 骑手后,每增 1 人奖励提升 <2%,成本可能高于收益。
-- 利用率:≤4 骑手时所有骑手利用率≥70%;≥5 骑手后部分骑手闲置,分布不均。
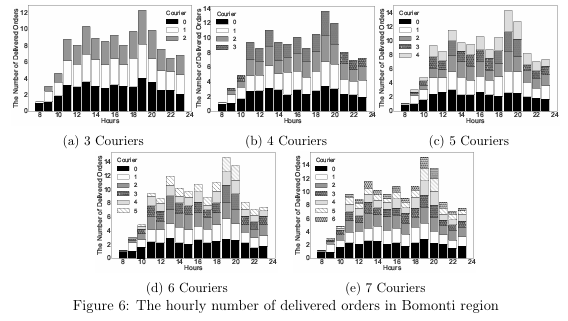
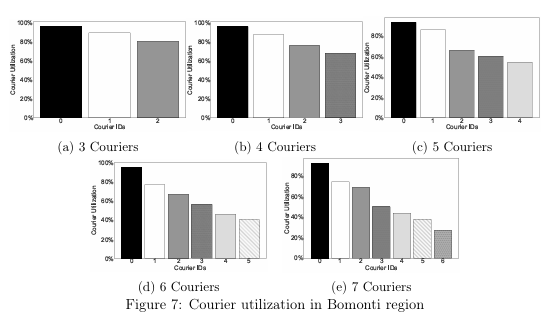
敏感性分析
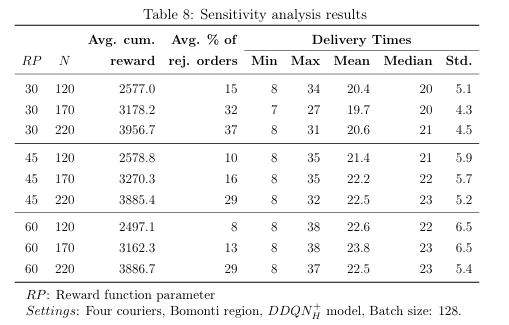
- 在 Bomonti 4 骑手场景下,做 RP(目标送达阈值 30/45/60 min)× N(日单量 120/170/220)双因素实验。
- RP=30:拒单率 15--37%,奖励低;RP=60:延迟高、奖励略降。RP=45 被视为收益与客户体验的最佳折中。
- 日单量 N 越大,拒单率越高,但奖励仍上升。
复杂度与收敛
- 状态-动作空间上界:O((n²+n)cf)(n×n 网格,c 骑手,r 餐厅,f 并发单)。
- Q-learning/SARSA 在小规模都难收敛;DQN 类 15 天(≈2300 回合)后奖励趋于稳定。
- 引入 Dueling/PER 增加 66% 训练时间,但对收敛无显著影响;骑手数或网格越大,波动越大。
结论
本文用 DDQN+H 把外卖配送建模为实时 MDP,在合成与伊斯坦布尔三区真实数据上验证其显著优于两条规则基线;给出"≈5 骑手即收益拐点、利用率≥70%"的实操建议,并指出未来可引入动态定价、骑手异质性与公平分单、硬约束 CMDP 等改进方向。