深度学习——模型训练

以Pytorch自带的手写数据集为例。我们已经构建了一个输入层（28*28），两个隐藏层（128和256），一个输出层（10）的人工神经网络。并且结合非线性激活函数sigmoid定义前向传播的方向。

class NeuralNet(nn.Module):
    def __init__(self):
        super().__init__()
        self.flatten = nn.Flatten()
        self.hidden1 = nn.Linear(28*28,128)#第一层（28*28为输入的神经原数，128为输出的神经元数）
        self.hidden2 = nn.Linear(128,256)
        self.output = nn.Linear(256,10)

    def forward(self, x):#前向传播，表明数据流向，不能改变函数名，在父类中拥有同名函数,
        #必须在子类中覆盖该函数，不然会调用父类中的空函数。
        x = self.flatten(x)
        x = self.hidden1(x)
        x = torch.sigmoid(x)#非线性激活函数
        x = self.hidden2(x)
        x = torch.sigmoid(x)
        x = self.output(x)
        #x = torch.sigmoid(x)#对输出进行非线性激活
        return x

现在我们需要对模型进行训练

1.准备

创建数据加载器DataLoader加载数据

DataLoader是用来批量加载数据的工具，可以高效地迭代数据集并支持多进程加速。

training_dataloader = DataLoader(dataset=training_data, batch_size=64)

• dataset=training_data：指定要加载的数据集（通常是 torch.utils.data.Dataset的子类实例）。
• batch_size=64：每个批次加载 ​64个样本​ 。

以下是 DataLoader的常用参数（你可以在需要时补充）：

参数	作用
shuffle	是否打乱数据顺序（训练集通常设为 True，测试集设为 False）。
num_workers	使用多少子进程加载数据（建议设为CPU核心数，如 4）。
drop_last	是否丢弃最后一个不完整的批次（当样本数不能被 batch_size整除时）。
pin_memory	是否将数据锁页（True可加速GPU传输，需配合CUDA使用）。

​​数据格式​​：

• 确保 training_data返回的数据是张量（或可转换为张量）。
• 如果使用自定义数据集，需实现 __getitem__和 __len__方法。

现在我们加载训练集和测试集。

training_dataloader = DataLoader(dataset=training_data,batch_size=64)
test_dataloader = DataLoader(dataset=test_data,batch_size=64)

如果你拥有gpu可以通过以下代码对使用gpu

device = "cuda" if torch.cuda.is_available() else "mps" if torch.backends.mps.is_available() else "cpu"
# print(f'Using {device} device')

model = NeuralNet().to(device)
print(model)

model.to(device)将模型的所有参数和缓冲区移动到指定设备（GPU/CPU）：

model = NeuralNet().to(device)

​​作用​ ：

• 若 device="cuda"，模型会在NVIDIA GPU上运行（需安装CUDA版PyTorch）。
• 若 device="mps"，模型会使用Apple Silicon的GPU加速（需macOS 12.3+和M1/M2芯片）。
• 若 device="cpu"，模型在CPU上运行（兼容所有环境但速度较慢）。

分别导入交叉熵 损失函数和**（随机梯度下降）SGD优化器**

loss_fn = nn.CrossEntropyLoss()
optimizer = torch.optim.SGD(model.parameters(), lr=0.01)

1. 交叉熵损失函数（CrossEntropyLoss）​​

​​用途​​

• 适用于多分类任务（如MNIST手写数字识别、CIFAR-10图像分类）。
• 输入应为​未归一化的类别分数（logits）​ ，无需手动添加Softmax层。

​​数学形式​​

• yc：真实标签的one-hot编码（实际由PyTorch自动处理）。
• pc：预测类别的概率（通过Softmax隐式计算）。

​​关键注意事项​​

1. ​输入形状​ ：
   • 预测值（logits）：[batch_size, num_classes]
   • 真实标签：[batch_size]（值为类别索引，如0到9）。

随机梯度下降优化器（SGD）​​

​​参数解析​​

optimizer = torch.optim.SGD( model.parameters(), # 待优化的模型参数

lr=0.01, # 学习率（关键超参数）

momentum=0.9, # 动量（可选，加速收敛）

weight_decay=0.001 # L2正则化（可选，防止过拟合） )

二、训练模型

在进行一系列处理后我们就可以训练模型了

def train(train_dataloader, model, loss_fn, optimizer):
    #train_dataloader为要训练的数据
    #model为训练的模型
    #loss_fn损失函数
    #optimizer优化器
    model.train()  # 设置模型为训练模式（启用Dropout/BatchNorm等）
    batch_size_num = 1  # 初始化批次计数器
    
    for X, y in train_dataloader:
        X, y = X.to(device), y.to(device)  # 数据移动到设备（GPU/CPU）
        pred = model(X)  # 前向传播（等价于model.forward(X)）
        loss = loss_fn(pred, y)  # 计算损失
        
        optimizer.zero_grad()  # 清零梯度（防止累积）
        loss.backward()        # 反向传播（计算梯度）
        optimizer.step()       # 更新参数
        
        loss_val = loss.item()  # 获取标量损失值
        if batch_size_num % 100 == 0:
            print(f'Train loss: {loss_val:>7f}[number: {batch_size_num}]')
        batch_size_num += 1     # 更新批次计数

导入相应参数开始训练

train(training_dataloader,model,loss_fn,optimizer)

下列为训练结果

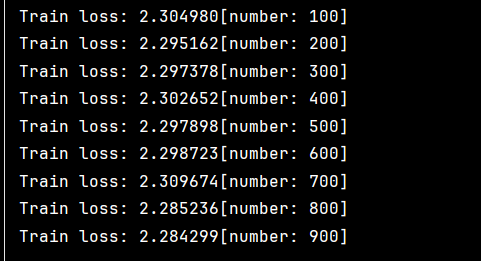
有训练好的模型后需要对其进行测试

def test(test_dataloader, model, loss_fn):
    size = len(test_dataloader.dataset)  # 测试集总样本数
    num_batches = len(test_dataloader)   # 测试集批次数量
    model.eval()  # 设置模型为评估模式（关闭Dropout/BatchNorm的随机性）
    
    test_loss, correct = 0, 0  # 初始化累计损失和正确预测数
    
    with torch.no_grad():  # 禁用梯度计算（节省内存和计算资源）
        for X, y in test_dataloader:
            X, y = X.to(device), y.to(device)  # 数据移动到设备
            pred = model(X)  # 前向传播
            test_loss += loss_fn(pred, y).item()  # 累加批次损失
            correct += (pred.argmax(1) == y).type(torch.float).sum().item()  # 累加正确预测数
    
    # 计算平均损失和准确率
    test_loss /= num_batches
    correct /= size
    print(f'Test result:\n Accuracy: {(100*correct)}%, Avg loss: {test_loss}')

填入参数进行测试

test(test_dataloader,model,loss_fn)

结果如下

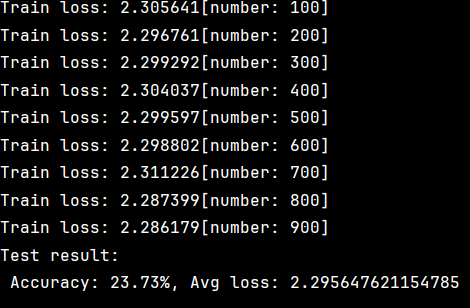
通过测试发现我们的结果准确率仅有23.73%，结果并不理想。在这我们可以通过多轮训练来优化模型。

epochs = 50
for epoch in range(epochs):
    print(f'Epoch {epoch+1}')
    train(training_dataloader,model,loss_fn,optimizer)
print("Finished Training")
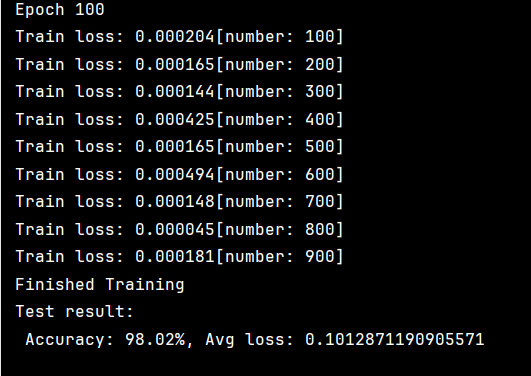
test(test_dataloader,model,loss_fn)

结果如下

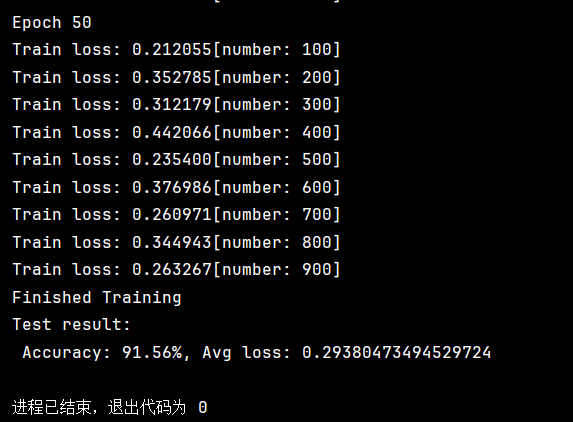
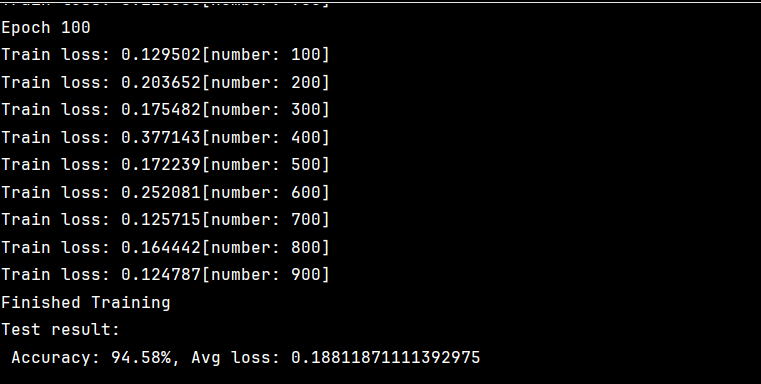
上图为50轮和100轮的结果。

通过调整优化器的学习率使lr=1可以将准确率进一步提高

但是上述方法的训练轮次太多，太过消耗时间。我们可以通过改变激活函数或者优化器优化训练模型

由于仅构建了两层隐含层，使用relu激活函数效果不如sigmoid激活函数。

这里我们修改优化器为Adam优化器

optimizer = torch.optim.Adam(model.parameters(), lr=0.01)

Adam优化器​ ​（Adaptive Moment Estimation）是深度学习中广泛使用的自适应学习率优化算法，结合了​​动量（Momentum）​ ​和​​RMSProp​​的优点，能够自动调整每个参数的学习率。以下是关于Adam优化器的详细解析及在PyTorch中的实践指南：

​​1. Adam的核心思想​​

• ​自适应学习率​ ：为每个参数维护独立的学习率，根据梯度的一阶矩（均值）和二阶矩（方差）动态调整。
• ​动量机制​ ：保留梯度的指数移动平均值（类似Momentum），加速收敛。
• ​偏差校正​ ：对初始时刻的矩估计进行校正，避免冷启动偏差。

---

​​2. Adam的数学形式​​

对于参数 θ和梯度 gt​：

1. ​计算梯度的一阶矩（均值）和二阶矩（方差）​ ：

   • mt：梯度均值（动量）。
   • vt：梯度方差（自适应学习率）。
   • β1,β2：衰减率（默认0.9和0.999）。

2. ​偏差校正​ ：

3. 参数更新​ ：

   • η：初始学习率。
   • ϵ：极小值（如1e-8）防止除零。

---

​​3. PyTorch中的Adam优化器​​

​​基本用法​​

import torch.optim as optim optimizer = optim.Adam( model.parameters(), # 待优化的模型参数 lr=0.001, # 初始学习率（默认0.001） betas=(0.9, 0.999), # 动量衰减系数（β₁, β₂） eps=1e-08, # 数值稳定项（默认1e-8） weight_decay=0.0 # L2正则化（默认0） )

​​关键参数说明​​

参数	作用
lr	学习率（通常设为0.001，需根据任务调整）。
betas	一阶矩和二阶矩的衰减率（默认(0.9, 0.999)）。
eps	数值稳定项，防止分母为零（通常无需修改）。
weight_decay	L2正则化系数（如0.01），防止过拟合。
amsgrad	是否使用AMSGrad变体（默认False，解决Adam可能不收敛的问题）。

---

​​4. Adam的优缺点​​

​​优点​​

• 自适应学习率​ ：无需手动调整学习率，适合大多数任务。
• 高效收敛​ ：结合动量和自适应学习率，在稀疏梯度场景下表现优异。
• ​超参数鲁棒性​ ：默认参数（如lr=0.001）通常表现良好。

​​缺点​​

最终结果

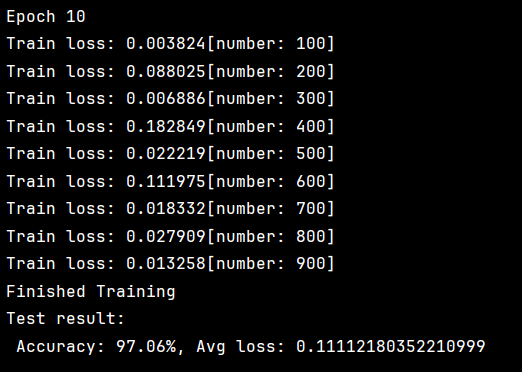
• ​内存占用较高​ ：需保存每个参数的 mt和 vt。
• 可能不收敛​ ：在某些非凸问题上（如GAN训练），AMSGrad变体可能更稳定。

我们发现仅用10轮就达到了97.06%的准确率