CUDA 矩阵分块乘法

一图胜千言，如下图所示，现在要通过矩阵分块的方式计算矩阵 A乘以矩阵 B的结果（记为矩阵 C），假设:

A矩阵的分块是：A11, A12, A21, A22, A31, A32；
B矩阵的分块是：B11, B12, B13, B21, B22, B23；
C矩阵的分块是：C11, C12, C13, C21, C22, C23, C31, C32, C33；
每个分块的大小是：BLOCK_SIZE * BLOCK_SIZE。

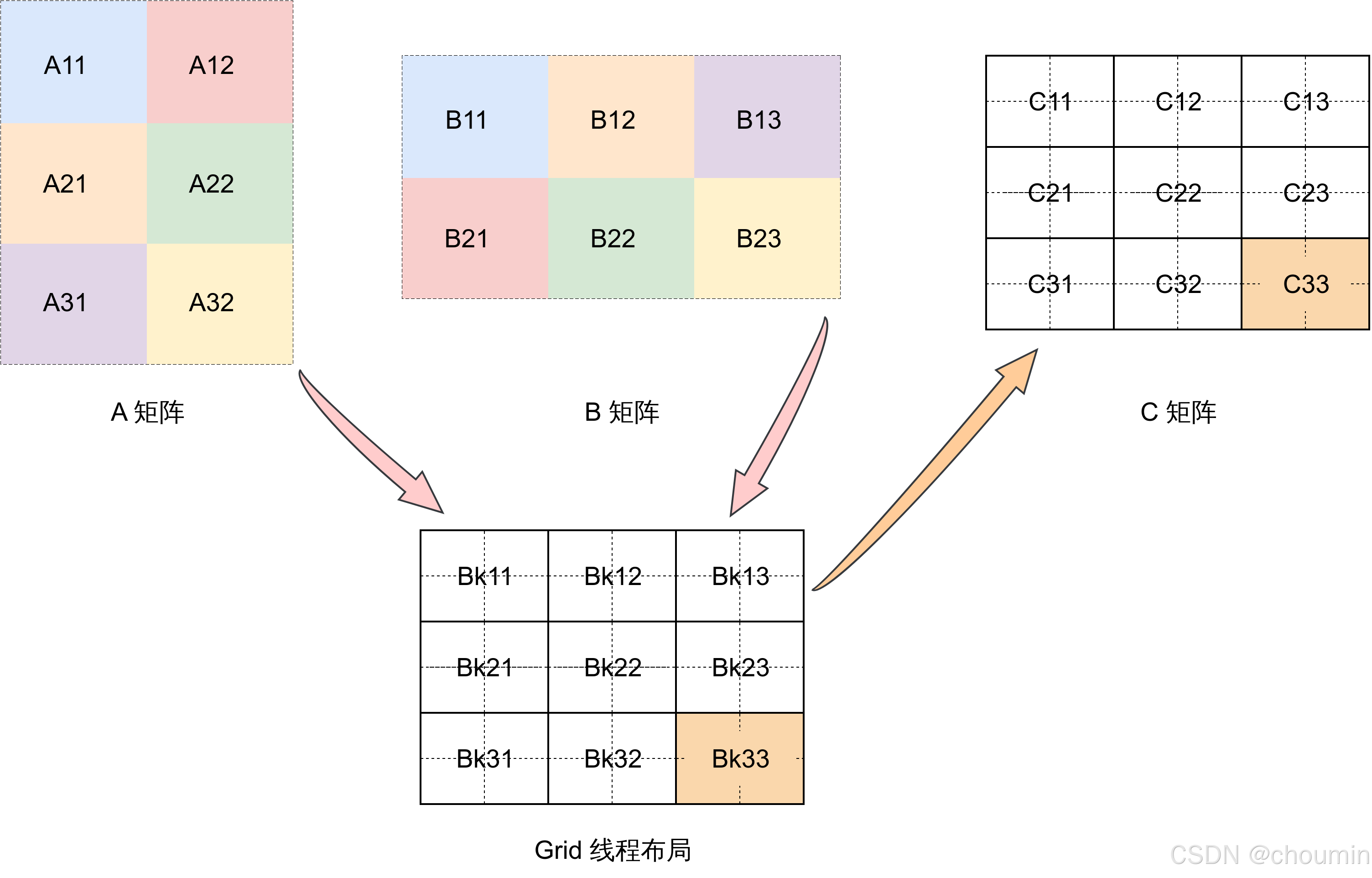
与之配套的核函数线程布局是：

9个 block线程块，即 Bk11, Bk12, Bk13, Bk21, Bk22, Bk23, Bk31, Bk32, Bk33，与 C矩阵的 9个分块一一对应；
每个 block线程块的大小是：BLOCK_SIZE * BLOCK_SIZE。

从上面的 结果矩阵分块 和 线程分块 的对应关系可以看到，每个 block线程块负责产生 C矩阵中的一个分块的计算结果，例如：Bk33线程块负责计算 C33分块的结果，由矩阵分块乘法的原理可知，C33 = A31 x B13 + A32 x B23，也就是说：Bk33线程块需要做的事情是：

读入 A31、B13，进行矩阵乘法；
读入 A32、B23，进行矩阵乘法；
... //如果涉及更多的分块，重复上面的操作；
将上述矩阵乘法得到的所有矩阵按元素对应相加 //上述步骤中在每一步做完矩阵乘法之后，可以直接在 C33分块上进行累加。

下面的代码来自 cuda-samples：

c++ 复制代码

/**
 * 通过矩阵分块的方法计算矩阵乘法: C = A * B
 * wA 是 A 矩阵的宽度，wB 是 B 矩阵的宽度
 */
template <int BLOCK_SIZE> __global__ void MatrixMulCUDA(float *C, float *A, float *B, int wA, int wB)
{
    // block 索引，假设当前是 Bk33 线程块，则 bx = 2，by = 2
    int bx = blockIdx.x;
    int by = blockIdx.y;

    // thread 索引
    int tx = threadIdx.x;
    int ty = threadIdx.y;

    // 当前 block 为了生成 C33 分块的计算结果，需要处理的 A 矩阵的第一个分块，即 A31 分块的第一个元素的地址，这里的 by 是 2
    int aBegin = wA * BLOCK_SIZE * by;

    // 当前 block 需要处理的 A 矩阵的最后一个分块第一行的结束位置，即 A32 分块第一行最后一个元素的地址
    int aEnd = aBegin + wA - 1;

    // A 矩阵在 x 方向上，连续两个分块的第一个元素的间隔，横着是 x 方向，竖着是 y 方向
    int aStep = BLOCK_SIZE;

    // 当前 block 为了生成 C33 分块的计算结果，需要处理的 B 矩阵的第一个分块，即 B13 分块的第一个元素的地址，这里的 bx 是 2
    int bBegin = BLOCK_SIZE * bx;

    //  B 矩阵在 y 方向上，连续两个分块的第一个元素的间隔
    int bStep = BLOCK_SIZE * wB;

    // C33 分块每个元素的初始值，初始为 0，用于后续累加
    float Csub = 0;

    // 遍历当前 block（Bk33）需要处理的所有 A 矩阵分块（A31、A32）和 B 矩阵分块（B13、B23）
    // 上面计算出了 A 矩阵和 B 矩阵的分块步进幅度，因此很容易在遍历过程中拿到对应分块的起始地址
    for (int a = aBegin, b = bBegin; a <= aEnd; a += aStep, b += bStep) {
        // 声明用于存储 A 矩阵分块的共享内存，用于一个 block 内所有线程共享数据
        __shared__ float As[BLOCK_SIZE][BLOCK_SIZE];

        //  声明用于存储 B 矩阵分块的共享内存，用于一个 block 内所有线程共享数据
        __shared__ float Bs[BLOCK_SIZE][BLOCK_SIZE];

        // 发动一个 block 内的所有线程将 global memory 里的数据加载到 shared memory
        // 即加载 A 矩阵和 B 矩阵的对应分块
        As[ty][tx] = A[a + wA * ty + tx];
        Bs[ty][tx] = B[b + wB * ty + tx];

        // 等待一个 block 内的所有线程都完成数据加载操作
        __syncthreads();

        // 发动一个 block 内的所有线程对 A 矩阵和 B 矩阵的对应分块进行矩阵乘法操作
        // 对于某一个线程来说，需要完成 A 矩阵分块的某一行乘以 B 矩阵分块的某一列的操作，并求和
        // 针对多个分块矩阵，对求和结果进行累加
#pragma unroll
        for (int k = 0; k < BLOCK_SIZE; ++k) {
            Csub += As[ty][k] * Bs[k][tx];
        }

        // 等待一个 block 内的所有线程都完成行乘列的操作
        __syncthreads();
    }

    // 将 A31 x B13 + A32 x B23 的结果写入 C33 分块的对应位置，
    // 这里的索引计算是难点，
   // C 矩阵的宽度等于 B 矩阵的宽度，所以先计算 y 方向跳过的元素个数：wB * BLOCK_SIZE * by，
   // 再计算 x 方向跳过的元素个数：BLOCK_SIZE * bx，
   // 再计算 C33 分块内跳过的元素个数：wB * ty + tx，
   // 再将上述 3 个式子的结果相加，得到 C33 分块中某一个元素相对于 C 矩阵的偏移
    int c               = wB * BLOCK_SIZE * by + BLOCK_SIZE * bx;
    C[c + wB * ty + tx] = Csub;
}