AT_abc406_f [ABC406F] Compare Tree Weights
洛谷题目传送门
ATcoder题目传送门
题目描述
给定一个有 N N N 个顶点的树 T T T,顶点和边分别编号为顶点 1 1 1, 顶点 2 2 2, ... \ldots ..., 顶点 N N N 和边 1 1 1, 边 2 2 2, ... \ldots ..., 边 ( N − 1 ) (N-1) (N−1)。
特别地,边 i i i ( 1 ≤ i ≤ N − 1 ) (1 \leq i \leq N-1) (1≤i≤N−1) 连接顶点 U i U_i Ui 和顶点 V i V_i Vi。
此外,每个顶点都有一个权重,最初,所有顶点的权重都为 1 1 1。
给定 Q Q Q 个查询,请按顺序处理它们。每个查询是以下两种类型之一:
1 x w:将顶点 x x x 的权重增加 w w w。2 y:如果删除边 y y y, T T T 将分裂成两个子树(连通分量)。将每个子树中包含的顶点的权重总和作为该子树的权重时,输出两个子树权重的差。
关于第二种类型的查询,可以证明,从 T T T 中选择任意一条边并删除它时, T T T 总是会分裂成两个子树。
另外,请注意,第二种类型的查询实际上并没有删除边。
输入格式
输入按以下格式从标准输入给出。
N N N
U 1 U_1 U1 V 1 V_1 V1
U 2 U_2 U2 V 2 V_2 V2
⋮ \vdots ⋮
U N − 1 U_{N-1} UN−1 V N − 1 V_{N-1} VN−1
Q Q Q
q u e r y 1 \mathrm{query}_1 query1
q u e r y 2 \mathrm{query}_2 query2
⋮ \vdots ⋮
q u e r y Q \mathrm{query}_Q queryQ
每个查询 q u e r y i \mathrm{query}_i queryi ( 1 ≤ i ≤ Q ) (1 \leq i \leq Q) (1≤i≤Q) 按以下任一格式给出。
1 1 1 x x x w w w
2 2 2 y y y
输出格式
设第二种类型查询的个数为 K K K,输出 K K K 行。第 i i i 行 ( 1 ≤ i ≤ K ) (1 \leq i \leq K) (1≤i≤K) 输出第 i i i 个第二种类型查询的答案。
输入输出样例 #1
输入 #1
6
1 2
1 3
2 4
4 5
4 6
5
2 1
1 1 3
2 1
1 4 10
2 5输出 #1
2
1
17说明/提示
「数据范围」
- 2 ≤ N ≤ 3 × 10 5 2 \leq N \leq 3 \times 10^5 2≤N≤3×105
- 1 ≤ U i , V i ≤ N 1 \leq U_i, V_i \leq N 1≤Ui,Vi≤N
- 1 ≤ Q ≤ 3 × 10 5 1 \leq Q \leq 3 \times 10^5 1≤Q≤3×105
- 1 ≤ x ≤ N 1 \leq x \leq N 1≤x≤N
- 1 ≤ w ≤ 1000 1 \leq w \leq 1000 1≤w≤1000
- 1 ≤ y ≤ N − 1 1 \leq y \leq N-1 1≤y≤N−1
- 输入均为整数
- 给定的图是一棵树。
- 至少存在一个第二种类型的查询。
「样例 1 解释」
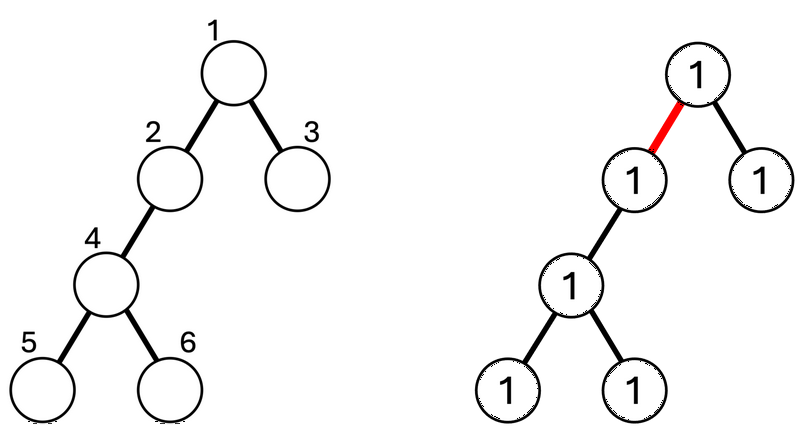
树 T T T 的结构和顶点编号对应如下图左所示。最初,所有顶点的权重都为 1 1 1。
对于第 1 1 1 个查询,考虑删除边 1 1 1。此时,树会分裂成包含顶点 1 1 1 的子树和包含顶点 2 2 2 的子树。包含顶点 1 1 1 的子树的权重为 2 2 2,包含顶点 2 2 2 的子树的权重为 4 4 4,因此输出它们的差 2 2 2。(下图右)
对于第 2 2 2 个查询,将顶点 1 1 1 的权重增加 3 3 3。
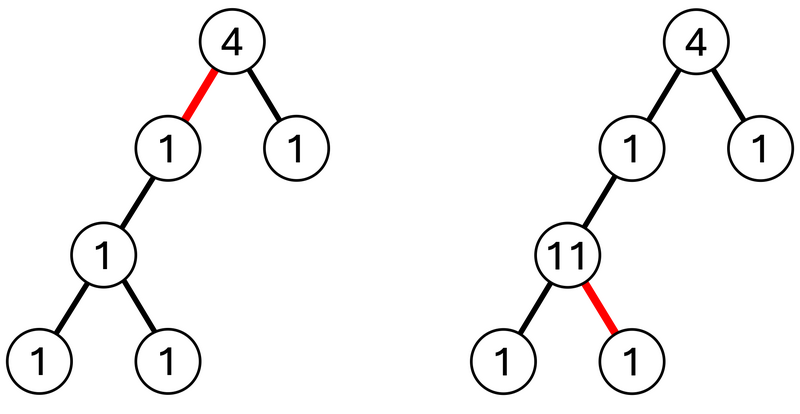
对于第 3 3 3 个查询,考虑删除边 1 1 1。包含顶点 1 1 1 的子树的权重为 5 5 5,包含顶点 2 2 2 的子树的权重为 4 4 4,因此输出它们的差 1 1 1。(下图左)
对于第 4 4 4 个查询,将顶点 4 4 4 的权重增加 10 10 10。
对于第 5 5 5 个查询,考虑删除边 5 5 5。此时,树会分裂成包含顶点 4 4 4 的子树和仅包含顶点 6 6 6 的子树。包含顶点 4 4 4 的子树的权重为 18 18 18,仅包含顶点 6 6 6 的子树的权重为 1 1 1,因此输出它们的差 17 17 17。(下图右)
因此,按顺序换行输出第二种类型查询的答案 2 , 1 , 17 2, 1, 17 2,1,17。
思路详解
题目分析
其实没什么好分析的,又要单点修改,还要求子树内的和,那显然是树链剖分+数据结构 ,在这里我采用树状数组。
code
cpp
#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int n,m;
struct Tree_array{//树状树状
int c[N];
int lowbit(int x){return x&(-x);}
void change(int x,int v){
for(;x<=n;x+=lowbit(x))c[x]+=v;
}
int _sum(int x){
int res=0;
for(;x;x-=lowbit(x))res+=c[x];
return res;
}
int sum(int x,int y){return _sum(y)-_sum(x-1);}
};
vector<int>e[N];
int siz[N],fa[N],son[N],dep[N];
int id[N],reid[N],top[N],tim=0,mx[N];
int w[N];
class Tree{//树链剖分
private:
Tree_array tr;
void dfs1(int u,int fath,int dp){//第一次深搜求出fa,siz,son,dep
siz[u]=1;fa[u]=fath;dep[u]=dp;
for(int v:e[u]){
if(v==fath)continue;
dfs1(v,u,dp+1);
siz[u]+=siz[v];
if(siz[v]>siz[son[u]])son[u]=v;
}
}
void dfs2(int u,int fath,int ori){//第二次深搜求出id,reid,top
id[u]=++tim;reid[tim]=u;top[u]=ori;
mx[u]=id[u];
if(son[u]){//从这里也可以看出一个子树内id是连续的
dfs2(son[u],u,ori);
mx[u]=max(mx[u],mx[son[u]]);
}
for(int v:e[u]){
if(v==fath||v==son[u])continue;
dfs2(v,u,v);
mx[u]=max(mx[u],mx[v]);
}
}
public:
void build(){//建树
dfs1(1,0,1);dfs2(1,0,1);
for(int i=1;i<=n;i++)tr.change(id[i],w[i]);
}
void add(int u,int v){tr.change(id[u],v);}//将节点u的权值加v
void print(){
for(int i=1;i<=n;i++)cout<<reid[i]<<' '<<tr.sum(i,i)<<'\n';
}
int query(int u){//求u的子树中的权值和
int res=tr.sum(id[u],mx[u]);
return res;
}
}tr;
struct node{
int x,y;
}a[N];
int main(){
//由于要在树上求子树和,而且要单点修改,那显然是树链剖分+数据结构,在这里我使用树状数组
//由于在一个子树中标记是连续的,所以我们开一个mx记录在这个子树中标记最大的即可
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
cin>>n;
for(int i=1;i<=n-1;i++){
int x,y;cin>>x>>y;
e[x].push_back(y);
e[y].push_back(x);
a[i]={x,y};
}
for(int i=1;i<=n;i++)w[i]=1;
tr.build();
int q;cin>>q;
for(int i=1;i<=q;i++){
int op,x,y;
cin>>op>>x;
if(op==1){cin>>y;tr.add(x,y);}
else{
auto [qx,qy]=a[x];
if(dep[qx]<dep[qy])swap(qx,qy);
cout<<abs(tr.query(1)-tr.query(qx)*2)<<'\n';
//总和减去当前这颗数的和即为剩余的和,所以要减2次
}
}
return 0;
}