线性代数 · 矩阵 | 秩 / 行秩 / 列秩 / 计算方法

斐夷所非2025-09-16 9:30

注：本文为 "线性代数 · 矩阵 | 秩" 相关合辑。

图片清晰度受引文原图所限。

略作重排，未全校去重。

如有内容异常，请看原文。

矩阵的秩及其应用

一、矩阵秩的基本概念

（一）k 阶子式

设矩阵 A = ( a i j ) m × n A = (a_{ij})_{m \times n} A=(aij)m×n，在矩阵 A A A 中任意选取 k k k 行（ 1 ≤ k ≤ m 1 \leq k \leq m 1≤k≤m）和 k k k 列（ 1 ≤ k ≤ n 1 \leq k \leq n 1≤k≤n），将位于这些行与列交叉处的 k 2 k^2 k2 个元素按原有的相对位置组成一个 k k k 阶行列式，该行列式称为矩阵 A A A 的一个 k 阶子式。

对于 m × n m \times n m×n 矩阵 A A A， k k k 阶子式的总数为组合数 C m k × C n k \mathrm{C}{m}^{k} \times \mathrm{C}{n}^{k} Cmk×Cnk（其中 C n k = n ! k ! ( n − k ) ! \mathrm{C}_{n}^{k} = \frac{n!}{k!(n - k)!} Cnk=k!(n−k)!n! 表示从 n n n 个元素中选取 k k k 个元素的组合数）。

示例 ：设矩阵 A = ( 1 2 3 4 1 3 4 1 1 4 1 2 ) A = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 1 & 3 & 4 & 1 \\ 1 & 4 & 1 & 2 \end{pmatrix} A= 111234341412

  • 选取第 1、2 行和第 2、4 列，交叉处元素组成的 2 阶子式为 D 2 ′ = ∣ 2 4 3 1 ∣ D_2' = \begin{vmatrix} 2 & 4 \\ 3 & 1 \end{vmatrix} D2′= 2341 ；
  • 选取第 1、3 行和第 1、3 列，交叉处元素组成的 2 阶子式为 D 2 ′ ′ = ∣ 1 3 1 1 ∣ D_2'' = \begin{vmatrix} 1 & 3 \\ 1 & 1 \end{vmatrix} D2′′= 1131 ；
  • 该矩阵的 2 阶子式总数为 C 3 2 × C 4 2 = 3 × 6 = 18 \mathrm{C}{3}^{2} \times \mathrm{C}{4}^{2} = 3 \times 6 = 18 C32×C42=3×6=18，3 阶子式总数为 C 3 3 × C 4 3 = 1 × 4 = 4 \mathrm{C}{3}^{3} \times \mathrm{C}{4}^{3} = 1 \times 4 = 4 C33×C43=1×4=4。

（二）矩阵秩的定义

设矩阵 A = ( a i j ) m × n A = (a_{ij})_{m \times n} A=(aij)m×n，若存在一个 r r r 阶子式不为 0 0 0，且所有 r + 1 r + 1 r+1 阶子式（若存在）全为 0 0 0，则称 r r r 为矩阵 A A A 的秩，记作 R ( A ) R(A) R(A) 或 r a n k ( A ) \mathrm{rank}(A) rank(A)。

特殊规定 ：零矩阵（所有元素均为 0 0 0 的矩阵）的秩为 0 0 0，即 R ( 0 ) = 0 R(0) = 0 R(0)=0。

重要结论：

  1. 对任意 m × n m \times n m×n 矩阵 A A A，必有 0 ≤ R ( A ) ≤ min ⁡ { m , n } 0 \leq R(A) \leq \min\{m, n\} 0≤R(A)≤min{m,n}；
  2. 若 n n n 阶方阵 A A A 的秩 R ( A ) = n R(A) = n R(A)=n，则称 A A A 为 满秩矩阵 （或非奇异矩阵），此时 det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0（ det ⁡ ( A ) \det(A) det(A) 表示矩阵 A A A 的行列式）；
  3. 若 n n n 阶方阵 A A A 的秩 R ( A ) < n R(A) < n R(A)<n，则称 A A A 为 降秩矩阵 （或奇异矩阵），此时 det ⁡ ( A ) = 0 \det(A) = 0 det(A)=0。

（三）秩的等价描述

矩阵的秩本质反映了矩阵中行（或列）向量的线性无关性，具体等价描述如下：

  • 行秩 ：矩阵 A A A 的行向量组中线性无关的行向量的最大个数；
  • 列秩 ：矩阵 A A A 的列向量组中线性无关的列向量的最大个数；
  • 定理 ：对任意矩阵 A A A，其行秩 = 列秩 = 秩（即 R ( A ) = 行秩 = 列秩 R(A) = \text{行秩} = \text{列秩} R(A)=行秩=列秩）。

二、矩阵秩的计算方法

（一）子式判别法（定义法）

根据矩阵秩的定义，通过寻找"最高阶非零子式"来确定秩，步骤如下：

  1. 从低阶子式开始计算，先判断 1 阶子式（即矩阵元素）是否全为 0 0 0：若全为 0 0 0，则 R ( A ) = 0 R(A) = 0 R(A)=0；若存在非零 1 阶子式，继续判断 2 阶子式；
  2. 若存在非零 2 阶子式，继续判断 3 阶子式，以此类推；
  3. 找到最大的 r r r，使得存在非零 r r r 阶子式，且所有 r + 1 r + 1 r+1 阶子式全为 0 0 0，则 R ( A ) = r R(A) = r R(A)=r。

示例 1 ：求矩阵 A = ( 1 2 3 0 0 1 0 1 0 0 1 0 ) A = \begin{pmatrix} 1 & 2 & 3 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix} A= 100210301010 的秩

  • 选取第 1、2、3 行和第 1、2、3 列，组成的 3 阶子式为 ∣ 1 2 3 0 1 0 0 0 1 ∣ = 1 ≠ 0 \begin{vmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{vmatrix} = 1 \neq 0 100210301 =1=0；
  • 矩阵 A A A 为 3 × 4 3 \times 4 3×4 矩阵，不存在 4 阶子式；
  • 因此 R ( A ) = 3 R(A) = 3 R(A)=3。

示例 2 ：求矩阵 D = ( 1 2 5 0 3 4 0 0 0 ) D = \begin{pmatrix} 1 & 2 & 5 \\ 0 & 3 & 4 \\ 0 & 0 & 0 \end{pmatrix} D= 100230540 的秩

  • 1 阶子式（如元素 1 1 1、 2 2 2、 5 5 5 等）非零，2 阶子式（如 ∣ 1 2 0 3 ∣ = 3 ≠ 0 \begin{vmatrix} 1 & 2 \\ 0 & 3 \end{vmatrix} = 3 \neq 0 1023 =3=0）非零；
  • 所有 3 阶子式（仅 1 个，即矩阵 D D D 的行列式）为 ∣ 1 2 5 0 3 4 0 0 0 ∣ = 0 \begin{vmatrix} 1 & 2 & 5 \\ 0 & 3 & 4 \\ 0 & 0 & 0 \end{vmatrix} = 0 100230540 =0；
  • 因此 R ( D ) = 2 R(D) = 2 R(D)=2（原内容此处写为 R ( A ) R(A) R(A)，属于符号混淆，已修正为 R ( D ) R(D) R(D)）。

（二）初等变换法（最常用方法）

1. 重要定理

矩阵的初等变换（行变换或列变换）不改变矩阵的秩，即若矩阵 A A A 经过初等变换化为矩阵 B B B，则 R ( A ) = R ( B ) R(A) = R(B) R(A)=R(B)。

初等变换的类型：

  • 行变换：
    1. 交换两行（记为 r i ↔ r j r_i \leftrightarrow r_j ri↔rj）；
    2. 用非零常数 k k k 乘某一行（记为 k r i k r_i kri， k ≠ 0 k \neq 0 k=0）；
    3. 某一行的 k k k 倍加到另一行（记为 r i + k r j r_i + k r_j ri+krj）。
  • 列变换：
    1. 交换两列（记为 c i ↔ c j c_i \leftrightarrow c_j ci↔cj）；
    2. 用非零常数 k k k 乘某一列（记为 k c i k c_i kci， k ≠ 0 k \neq 0 k=0）；
    3. 某一列的 k k k 倍加到另一列（记为 c i + k c j c_i + k c_j ci+kcj）。
2. 行阶梯形矩阵的定义

满足以下两个条件的矩阵称为 行阶梯形矩阵：

  1. 全零行（所有元素均为 0 0 0 的行）位于矩阵的下方；
  2. 非零行的第一个非零元素（称为"主元"）的列序数，从上到下严格递增。

示例 ： ( 1 0 2 − 4 0 1 − 1 2 0 0 0 0 ) \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 0 \end{pmatrix} 1000102−10−420 是行阶梯形矩阵（主元分别在第 1 列、第 2 列，列序数递增，全零行在最下方）。

3. 计算步骤
  1. 对矩阵 A A A 施行初等行变换，将其化为行阶梯形矩阵 B B B；
  2. 行阶梯形矩阵 B B B 中非零行的行数，即为矩阵 A A A 的秩（ R ( A ) = 非零行数 R(A) = \text{非零行数} R(A)=非零行数）。

示例 1 ：求矩阵 A = ( 1 0 2 − 4 2 1 3 − 6 − 1 − 1 − 1 2 ) A = \begin{pmatrix} 1 & 0 & 2 & -4 \\ 2 & 1 & 3 & -6 \\ -1 & -1 & -1 & 2 \end{pmatrix} A= 12−101−123−1−4−62 的秩

  • 第一步：消去第 1 列下方元素（以第 1 行第 1 列元素 1 1 1 为主元）
    A → r 2 − 2 r 1 ( 1 0 2 − 4 0 1 − 1 2 − 1 − 1 − 1 2 ) → r 3 + r 1 ( 1 0 2 − 4 0 1 − 1 2 0 − 1 1 − 2 ) A \xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ -1 & -1 & -1 & 2 \end{pmatrix} \xrightarrow{r_3 + r_1} \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ 0 & -1 & 1 & -2 \end{pmatrix} Ar2−2r1 10−101−12−1−1−422 r3+r1 10001−12−11−42−2 ；
  • 第二步：消去第 2 列下方元素（以第 2 行第 2 列元素 1 1 1 为主元）
    → r 3 + r 2 ( 1 0 2 − 4 0 1 − 1 2 0 0 0 0 ) \xrightarrow{r_3 + r_2} \begin{pmatrix} 1 & 0 & 2 & -4 \\ 0 & 1 & -1 & 2 \\ 0 & 0 & 0 & 0 \end{pmatrix} r3+r2 1000102−10−420 ；
  • 行阶梯形矩阵中非零行的行数为 2 2 2，因此 R ( A ) = 2 R(A) = 2 R(A)=2。

示例 2 ：求矩阵 A = ( 4 − 2 1 1 2 − 2 − 1 8 − 7 2 14 − 13 ) A = \begin{pmatrix} 4 & -2 & 1 \\ 1 & 2 & -2 \\ -1 & 8 & -7 \\ 2 & 14 & -13 \end{pmatrix} A= 41−12−228141−2−7−13 的秩

  • 第一步：交换第 1、2 行（使第 1 列主元为 1 1 1，简化计算）
    A → r 1 ↔ r 2 ( 1 2 − 2 4 − 2 1 − 1 8 − 7 2 14 − 13 ) A \xrightarrow{r_1 \leftrightarrow r_2} \begin{pmatrix} 1 & 2 & -2 \\ 4 & -2 & 1 \\ -1 & 8 & -7 \\ 2 & 14 & -13 \end{pmatrix} Ar1↔r2 14−122−2814−21−7−13 ；
  • 第二步：消去第 1 列下方元素
    → r 2 − 4 r 1 ( 1 2 − 2 0 − 10 9 − 1 8 − 7 2 14 − 13 ) → r 3 + r 1 ( 1 2 − 2 0 − 10 9 0 10 − 9 2 14 − 13 ) → r 4 − 2 r 1 ( 1 2 − 2 0 − 10 9 0 10 − 9 0 10 − 9 ) \xrightarrow{r_2 - 4 r_1} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ -1 & 8 & -7 \\ 2 & 14 & -13 \end{pmatrix} \xrightarrow{r_3 + r_1} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 10 & -9 \\ 2 & 14 & -13 \end{pmatrix} \xrightarrow{r_4 - 2 r_1} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 10 & -9 \\ 0 & 10 & -9 \end{pmatrix} r2−4r1 10−122−10814−29−7−13 r3+r1 10022−101014−29−9−13 r4−2r1 10002−101010−29−9−9 ；
  • 第三步：消去第 2 列下方元素
    → r 3 + r 2 ( 1 2 − 2 0 − 10 9 0 0 0 0 10 − 9 ) → r 4 + r 2 ( 1 2 − 2 0 − 10 9 0 0 0 0 0 0 ) \xrightarrow{r_3 + r_2} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 0 & 0 \\ 0 & 10 & -9 \end{pmatrix} \xrightarrow{r_4 + r_2} \begin{pmatrix} 1 & 2 & -2 \\ 0 & -10 & 9 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix} r3+r2 10002−10010−290−9 r4+r2 10002−1000−2900 ；
  • 行阶梯形矩阵中非零行的行数为 2 2 2，因此 R ( A ) = 2 R(A) = 2 R(A)=2。

（三）含参数矩阵的秩（需分类讨论）

当矩阵中含参数时，需根据参数的取值判断最高阶非零子式的阶数，进而确定秩。

示例 ：设矩阵 A = ( 1 − 1 1 2 3 λ − 1 2 5 3 μ 6 ) A = \begin{pmatrix} 1 & -1 & 1 & 2 \\ 3 & \lambda & -1 & 2 \\ 5 & 3 & \mu & 6 \end{pmatrix} A= 135−1λ31−1μ226 ，且 R ( A ) = 2 R(A) = 2 R(A)=2，求 λ \lambda λ 和 μ \mu μ 的值

  • 第一步：对 A A A 施行初等行变换化为行阶梯形
    A → r 2 − 3 r 1 ( 1 − 1 1 2 0 λ + 3 − 4 − 4 5 3 μ 6 ) → r 3 − 5 r 1 ( 1 − 1 1 2 0 λ + 3 − 4 − 4 0 8 μ − 5 − 4 ) A \xrightarrow{r_2 - 3 r_1} \begin{pmatrix} 1 & -1 & 1 & 2 \\ 0 & \lambda + 3 & -4 & -4 \\ 5 & 3 & \mu & 6 \end{pmatrix} \xrightarrow{r_3 - 5 r_1} \begin{pmatrix} 1 & -1 & 1 & 2 \\ 0 & \lambda + 3 & -4 & -4 \\ 0 & 8 & \mu - 5 & -4 \end{pmatrix} Ar2−3r1 105−1λ+331−4μ2−46 r3−5r1 100−1λ+381−4μ−52−4−4 ；
  • 第二步：由 R ( A ) = 2 R(A) = 2 R(A)=2 可知，行阶梯形矩阵中第 3 行需为全零行，因此第 2、3 行对应元素成比例
    即 λ + 3 8 = − 4 μ − 5 = − 4 − 4 \frac{\lambda + 3}{8} = \frac{-4}{\mu - 5} = \frac{-4}{-4} 8λ+3=μ−5−4=−4−4；
  • 第三步：求解比例方程
    由 − 4 − 4 = 1 \frac{-4}{-4} = 1 −4−4=1，得 λ + 3 = 8 × 1    ⟹    λ = 5 \lambda + 3 = 8 \times 1 \implies \lambda = 5 λ+3=8×1⟹λ=5； − 4 = ( μ − 5 ) × 1    ⟹    μ = 1 -4 = (\mu - 5) \times 1 \implies \mu = 1 −4=(μ−5)×1⟹μ=1；
  • 因此，当 λ = 5 \lambda = 5 λ=5 且 μ = 1 \mu = 1 μ=1 时， R ( A ) = 2 R(A) = 2 R(A)=2。

三、矩阵化简的形式与方法

（一）矩阵化简的基本原理

矩阵化简通过初等变换（行变换或列变换）实现，初等变换不改变矩阵的秩，是计算秩、求解线性方程组的关键工具。常见化简目标包括行阶梯形、行简化行阶梯形、列阶梯形及等价标准形，不同形式适用于不同场景。

（二）常见化简形式及规则

1. 行阶梯形（Row Echelon Form, REF）

REF 是"阶梯状"的基础化简形式，需满足以下 4 条规则：

  1. 全零行位于矩阵最下方；
  2. 非零行的第一个非零元素（称为"主元"）的列索引，严格大于上一行主元的列索引（形成"阶梯"结构）；
  3. 主元下方的所有元素全为 0 0 0；
  4. 主元可为任意非零数（无需强制为 1 1 1）。

示例 （主元用橙色标注）：
( 2 3 5 7 0 − 1 4 2 0 0 0 3 0 0 0 0 ) \begin{pmatrix} \color{orange}{2} & 3 & 5 & 7 \\ 0 & \color{orange}{-1} & 4 & 2 \\ 0 & 0 & 0 & \color{orange}{3} \\ 0 & 0 & 0 & 0 \end{pmatrix} 20003−10054007230

用途 ：快速判断矩阵的秩（非零行数 = 秩）；初步求解线性方程组（需后续"回代"步骤）。
注意：一个矩阵的 REF 不唯一（主元可缩放，不同初等行变换可能得到不同 REF）。

2. 行简化行阶梯形（Reduced Row Echelon Form, RREF）

RREF 是 REF 的"最简形式"，在 REF 规则基础上额外满足 2 条严格规则：

  1. 所有主元的值必为 1 1 1；
  2. 主元上方的所有元素全为 0 0 0（即主元列仅主元为 1 1 1，其余元素均为 0 0 0）。

示例 （将上述 REF 化为 RREF，主元用橙色标注）：
( 1 0 17 / 2 0 0 1 − 4 0 0 0 0 1 0 0 0 0 ) \begin{pmatrix} \color{orange}{1} & 0 & 17/2 & 0 \\ 0 & \color{orange}{1} & -4 & 0 \\ 0 & 0 & 0 & \color{orange}{1} \\ 0 & 0 & 0 & 0 \end{pmatrix} 1000010017/2−4000010

重要性质 ：一个矩阵的 RREF 是唯一的（无论采用何种初等行变换，最终结果完全相同）。
用途：直接读取线性方程组的解（无需回代）；确定矩阵的主元列（对应列空间的基）；判断向量组的线性相关性。

3. 列阶梯形（Column Echelon Form, CEF）

CEF 与 REF 逻辑对称，通过初等列变换实现，需满足以下 4 条规则：

  1. 全零列位于矩阵最右侧；
  2. 非零列的第一个非零元素（称为"列主元"）的行索引，严格大于左一列列主元的行索引；
  3. 列主元右侧的所有元素全为 0 0 0；
  4. 列主元可为任意非零数（无需强制为 1 1 1）。

示例 （列主元用橙色标注）：
( 2 0 0 0 3 − 1 0 0 5 4 0 0 7 2 3 0 ) \begin{pmatrix} \color{orange}{2} & 0 & 0 & 0 \\ 3 & \color{orange}{-1} & 0 & 0 \\ 5 & 4 & 0 & 0 \\ 7 & 2 & \color{orange}{3} & 0 \end{pmatrix} 23570−14200030000

用途：分析矩阵的行空间（非零行是行空间的基）；计算矩阵的左逆（当矩阵列满秩时）。

4. 等价标准形（相抵标准形）

若同时允许初等行变换和初等列变换，任意 m × n m \times n m×n 矩阵可化为唯一的"等价标准形"，形式为：
E = ( I r 0 r × ( n − r ) 0 ( m − r ) × r 0 ( m − r ) × ( n − r ) ) \mathbf{E} = \begin{pmatrix} \mathbf{I}r & \mathbf{0}{r \times (n-r)} \\ \mathbf{0}{(m-r) \times r} & \mathbf{0}{(m-r) \times (n-r)} \end{pmatrix} E=(Ir0(m−r)×r0r×(n−r)0(m−r)×(n−r))

其中：

  • m , n m, n m,n 分别为原矩阵的行数和列数；
  • r = R ( A ) r = R(A) r=R(A)（矩阵的秩）；
  • I r \mathbf{I}_r Ir 为 r r r 阶单位矩阵， 0 \mathbf{0} 0 为对应维度的零矩阵。

示例 （秩为 2 2 2 的 3 × 4 3 \times 4 3×4 矩阵的等价标准形）：
( 1 0 0 0 0 1 0 0 0 0 0 0 ) \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} 100010000000

用途：判断两个矩阵是否"等价"（若两个矩阵的等价标准形相同，则二者等价）；简化矩阵的秩与行列式计算。

（三）矩阵化简的应用场景总结

为清晰区分不同化简形式的适用场景，下表梳理了重要信息：

化简目标 推荐化简形式 操作方式 典型用途
快速计算矩阵的秩 行阶梯形（REF） 初等行变换 初步分析矩阵的有效维度，判断向量组线性相关性
求解线性方程组 行简化行阶梯形（RREF） 初等行变换 直接读取唯一解或无穷解的通解，无需回代
确定列空间的基 行简化行阶梯形（RREF） 初等行变换 主元列对应原矩阵的列向量，构成列空间的基
确定行空间的基 列阶梯形（CEF） 初等列变换 主元行对应原矩阵的行向量，构成行空间的基
判断两个矩阵是否等价 等价标准形 初等行变换 + 初等列变换 比较两个矩阵的结构相似度，验证是否可通过初等变换互化

四、矩阵秩的性质

设 A A A、 B B B 为任意矩阵， k k k 为非零常数， n n n 为方阵的阶数，则矩阵的秩满足以下性质，下表结合"性质内容"与"直观说明"展开：

性质序号 性质内容 说明
1 R ( A T ) = R ( A ) R(A^T) = R(A) R(AT)=R(A)（转置后秩不变） 矩阵的行秩 = 列秩，转置后行与列互换，秩的本质（线性无关向量的最大个数）不变
2 R ( A ) ≤ min ⁡ { m , n } R(A) \leq \min\{m, n\} R(A)≤min{m,n}（ A A A 为 m × n m \times n m×n 矩阵） 秩反映矩阵的"有效维度"，无法超过矩阵的行数（行向量最大可能无关个数）或列数（列向量最大可能无关个数）
3 R ( k A ) = R ( A ) R(kA) = R(A) R(kA)=R(A)（ k ≠ 0 k \neq 0 k=0） 非零常数 k k k 仅缩放矩阵元素，不改变子式的"非零性"（非零子式缩放后仍非零，零子式缩放后仍为零）
4 R ( A ) = 0    ⟺    A = 0 R(A) = 0 \iff A = 0 R(A)=0⟺A=0（零矩阵的充要条件） 零矩阵所有子式均为 0 0 0，故秩为 0 0 0；若 R ( A ) = 0 R(A)=0 R(A)=0，则无任何非零子式，矩阵必为零矩阵
5 R ( A + B ) ≤ R ( A ) + R ( B ) R(A + B) \leq R(A) + R(B) R(A+B)≤R(A)+R(B)（和的秩不超过秩的和） 矩阵 A + B A + B A+B 的行向量可由 A A A 和 B B B 的行向量组线性表示，因此其线性无关向量的最大个数不超过两组向量无关个数之和
6 R ( A B ) ≤ min ⁡ { R ( A ) , R ( B ) } R(AB) \leq \min\{R(A), R(B)\} R(AB)≤min{R(A),R(B)}（乘积的秩不超过因子矩阵的秩） A B AB AB 的列向量可由 A A A 的列向量线性表示（故 R ( A B ) ≤ R ( A ) R(AB) \leq R(A) R(AB)≤R(A)），行向量可由 B B B 的行向量线性表示（故 R ( A B ) ≤ R ( B ) R(AB) \leq R(B) R(AB)≤R(B)），因此取最小值
7 R ( A ) + R ( B ) − n ≤ R ( A B ) R(A) + R(B) - n \leq R(AB) R(A)+R(B)−n≤R(AB)（Sylvester 不等式） 对 n n n 阶方阵 A A A、 B B B，乘积的秩存在下界，反映了因子矩阵秩与乘积矩阵秩的"关联约束"，可用于证明矩阵可逆性等问题
8 若 A A A 为 n n n 阶可逆矩阵，则 R ( A B ) = R ( B ) R(AB) = R(B) R(AB)=R(B)， R ( B A ) = R ( B ) R(BA) = R(B) R(BA)=R(B) 可逆矩阵可通过初等变换化为单位阵，而初等变换不改变矩阵的秩，因此 A A A 的可逆性不影响 B B B 的秩传递

五、矩阵秩的应用

矩阵的秩是连接"矩阵结构"与"线性代数问题"的桥梁，以下从四个典型场景展开，结合示例说明其应用逻辑：

（一）判断线性方程组的解

对于线性方程组 A x = b A \boldsymbol{x} = \boldsymbol{b} Ax=b（ A A A 为 m × n m \times n m×n 系数矩阵， A ‾ = ( A ∣ b ) \overline{A} = (A \mid \boldsymbol{b}) A=(A∣b) 为增广矩阵），解的存在性与唯一性完全由 R ( A ) R(A) R(A) 和 R ( A ‾ ) R(\overline{A}) R(A) 的关系决定，重要结论如下：

  1. 无解 ： R ( A ) < R ( A ‾ ) R(A) < R(\overline{A}) R(A)<R(A)（增广矩阵的秩比系数矩阵多 1 1 1，对应矛盾方程 0 = d ≠ 0 0 = d \neq 0 0=d=0，即"约束条件冲突"）；
  2. 唯一解 ： R ( A ) = R ( A ‾ ) = n R(A) = R(\overline{A}) = n R(A)=R(A)=n（秩等于未知数个数，无自由变量，即"约束条件恰好确定唯一解"）；
  3. 无穷多解 ： R ( A ) = R ( A ‾ ) < n R(A) = R(\overline{A}) < n R(A)=R(A)<n（秩小于未知数个数，存在自由变量，即"约束条件不足，解有多个"）。

示例 ：判断方程组 { x 1 + 4 x 2 + 7 x 3 = 1 2 x 1 + 5 x 2 + 8 x 3 = 2 3 x 1 + 6 x 2 + 9 x 3 = 3 \begin{cases} x_1 + 4 x_2 + 7 x_3 = 1 \\ 2 x_1 + 5 x_2 + 8 x_3 = 2 \\ 3 x_1 + 6 x_2 + 9 x_3 = 3 \end{cases} ⎩ ⎨ ⎧x1+4x2+7x3=12x1+5x2+8x3=23x1+6x2+9x3=3 的解

  • 第一步：构造增广矩阵 A ‾ = ( 1 4 7 1 2 5 8 2 3 6 9 3 ) \overline{A} = \begin{pmatrix} 1 & 4 & 7 & 1 \\ 2 & 5 & 8 & 2 \\ 3 & 6 & 9 & 3 \end{pmatrix} A= 123456789123 ；
  • 第二步：初等行变换化为行阶梯形：
    A ‾ → r 2 − 2 r 1 ( 1 4 7 1 0 − 3 − 6 0 3 6 9 3 ) → r 3 − 3 r 1 ( 1 4 7 1 0 − 3 − 6 0 0 − 6 − 12 0 ) → r 3 − 2 r 2 ( 1 4 7 1 0 − 3 − 6 0 0 0 0 0 ) \overline{A} \xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 4 & 7 & 1 \\ 0 & -3 & -6 & 0 \\ 3 & 6 & 9 & 3 \end{pmatrix} \xrightarrow{r_3 - 3 r_1} \begin{pmatrix} 1 & 4 & 7 & 1 \\ 0 & -3 & -6 & 0 \\ 0 & -6 & -12 & 0 \end{pmatrix} \xrightarrow{r_3 - 2 r_2} \begin{pmatrix} 1 & 4 & 7 & 1 \\ 0 & -3 & -6 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix} Ar2−2r1 1034−367−69103 r3−3r1 1004−3−67−6−12100 r3−2r2 1004−307−60100 ；
  • 第三步：分析秩的关系： R ( A ) = 2 R(A) = 2 R(A)=2， R ( A ‾ ) = 2 R(\overline{A}) = 2 R(A)=2，且未知数个数 n = 3 n = 3 n=3，满足 R ( A ) = R ( A ‾ ) < n R(A) = R(\overline{A}) < n R(A)=R(A)<n，因此方程组有无穷多解。

（二）判断向量组的线性相关性

设向量组 α 1 , α 2 , ... , α s \alpha_1, \alpha_2, \dots, \alpha_s α1,α2,...,αs 构成矩阵 A A A（列向量组构成 A = ( α 1 , α 2 , ... , α s ) A = (\alpha_1, \alpha_2, \dots, \alpha_s) A=(α1,α2,...,αs)，行向量组构成 A = ( α 1 T α 2 T ... α s T ) A = \begin{pmatrix} \alpha_1^T \\ \alpha_2^T \\ \dots \\ \alpha_s^T \end{pmatrix} A= α1Tα2T...αsT ），则向量组的线性相关性与 R ( A ) R(A) R(A) 的关系为：

  1. 若 R ( A ) = s R(A) = s R(A)=s，则向量组 线性无关（矩阵的秩等于向量个数，所有向量均可作为"有效约束"，无冗余）；
  2. 若 R ( A ) < s R(A) < s R(A)<s，则向量组 线性相关（矩阵的秩小于向量个数，存在冗余向量，可由其他向量线性表示）。

示例 ：判断向量组 α 1 = ( 1 , 2 , 3 ) T \alpha_1 = (1, 2, 3)^T α1=(1,2,3)T， α 2 = ( 2 , 5 , 8 ) T \alpha_2 = (2, 5, 8)^T α2=(2,5,8)T， α 3 = ( 3 , 6 , 9 ) T \alpha_3 = (3, 6, 9)^T α3=(3,6,9)T 的线性相关性

  • 构造矩阵 A = ( α 1 , α 2 , α 3 ) = ( 1 2 3 2 5 6 3 8 9 ) A = (\alpha_1, \alpha_2, \alpha_3) = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 5 & 6 \\ 3 & 8 & 9 \end{pmatrix} A=(α1,α2,α3)= 123258369 ；
  • 初等行变换化为行阶梯形： A → r 2 − 2 r 1 ( 1 2 3 0 1 0 3 8 9 ) → r 3 − 3 r 1 ( 1 2 3 0 1 0 0 2 0 ) → r 3 − 2 r 2 ( 1 2 3 0 1 0 0 0 0 ) A \xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 3 & 8 & 9 \end{pmatrix} \xrightarrow{r_3 - 3 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 2 & 0 \end{pmatrix} \xrightarrow{r_3 - 2 r_2} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{pmatrix} Ar2−2r1 103218309 r3−3r1 100212300 r3−2r2 100210300 ；
  • 得 R ( A ) = 2 < 3 R(A) = 2 < 3 R(A)=2<3（向量个数），因此向量组线性相关。

（三）判断矩阵的可逆性

对 n n n 阶方阵 A A A，"可逆性"与"秩"紧密关联，以下条件完全等价（可互相推导）：

  1. A A A 可逆（存在逆矩阵 A − 1 A^{-1} A−1，满足 A A − 1 = A − 1 A = I n A A^{-1} = A^{-1} A = \mathbf{I}_n AA−1=A−1A=In）；
  2. A A A 为满秩矩阵（ R ( A ) = n R(A) = n R(A)=n，即矩阵无冗余行/列，有效维度等于阶数）；
  3. det ⁡ ( A ) ≠ 0 \det(A) \neq 0 det(A)=0（行列式非零，对应"最高阶子式非零"，符合满秩定义）；
  4. A A A 可通过初等行变换化为单位阵 I n \mathbf{I}_n In（初等变换不改变秩，单位阵秩为 n n n，故 A A A 秩也为 n n n）。

示例 ：设 A = ( 1 2 3 2 1 2 3 1 2 ) A = \begin{pmatrix} 1 & 2 & 3 \\ 2 & 1 & 2 \\ 3 & 1 & 2 \end{pmatrix} A= 123211322 ，验证 A A A 可逆并化为单位阵

  • 第一步：计算 R ( A ) R(A) R(A)：
    A → r 2 − 2 r 1 ( 1 2 3 0 − 3 − 4 3 1 2 ) → r 3 − 3 r 1 ( 1 2 3 0 − 3 − 4 0 − 5 − 7 ) → r 3 − 5 3 r 2 ( 1 2 3 0 − 3 − 4 0 0 − 1 3 ) A \xrightarrow{r_2 - 2 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 3 & 1 & 2 \end{pmatrix} \xrightarrow{r_3 - 3 r_1} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & -5 & -7 \end{pmatrix} \xrightarrow{r_3 - \frac{5}{3} r_2} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & 0 & -\frac{1}{3} \end{pmatrix} Ar2−2r1 1032−313−42 r3−3r1 1002−3−53−4−7 r3−35r2 1002−303−4−31 ；
  • 行阶梯形中非零行数为 3 = n 3 = n 3=n（阶数），故 R ( A ) = 3 R(A) = 3 R(A)=3， A A A 可逆；
  • 第二步：继续化为单位阵：
    → r 3 × ( − 3 ) ( 1 2 3 0 − 3 − 4 0 0 1 ) → r 2 + 4 r 3 ( 1 2 3 0 − 3 0 0 0 1 ) → r 2 × ( − 1 3 ) ( 1 2 3 0 1 0 0 0 1 ) → r 1 − 3 r 3 ( 1 2 0 0 1 0 0 0 1 ) → r 1 − 2 r 2 ( 1 0 0 0 1 0 0 0 1 ) = I 3 \xrightarrow{r_3 \times (-3)} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & -4 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_2 + 4 r_3} \begin{pmatrix} 1 & 2 & 3 \\ 0 & -3 & 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_2 \times (-\frac{1}{3})} \begin{pmatrix} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_1 - 3 r_3} \begin{pmatrix} 1 & 2 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} \xrightarrow{r_1 - 2 r_2} \begin{pmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix} = \mathbf{I}_3 r3×(−3) 1002−303−41 r2+4r3 1002−30301 r2×(−31) 100210301 r1−3r3 100210001 r1−2r2 100010001 =I3。

（四）数据降维和信息压缩

在机器学习、信号处理等领域，矩阵的秩反映"数据冗余度"：低秩矩阵（ R ( A ) ≪ min ⁡ { m , n } R(A) \ll \min\{m, n\} R(A)≪min{m,n}）表示数据存在大量冗余，可通过"保留核心信息、剔除冗余"实现降维与压缩，典型应用为奇异值分解（SVD） 和主成分分析（PCA）。

  • 逻辑 ：对矩阵 A A A 进行奇异值分解，得 A = U Σ V T A = U \Sigma V^T A=UΣVT，其中 Σ \Sigma Σ 为对角矩阵，对角元素（奇异值）按从大到小排列；取前 r r r 个非零奇异值（ r = R ( A ) r = R(A) r=R(A)）对应的子矩阵，可得到原矩阵的低秩逼近 A r = U r Σ r V r T A_r = U_r \Sigma_r V_r^T Ar=UrΣrVrT，实现用 r ( m + n − r ) r(m + n - r) r(m+n−r) 个元素表示原 m × n m \times n m×n 矩阵（大幅减少存储量）。
  • 示例 ：图片压缩。灰度图片可表示为 m × n m \times n m×n 矩阵（元素为像素灰度值），若矩阵秩 r r r 远小于 m m m 和 n n n，用低秩逼近矩阵 A r A_r Ar 替代原矩阵，视觉上几乎无差异，但存储量显著降低。

六、特殊矩阵的秩

部分结构特殊的矩阵，其秩可直接通过"直观特征"计算，无需复杂变换，以下列举两类典型矩阵：

（一）三角矩阵

三角矩阵分为上三角矩阵和下三角矩阵，其秩由"主对角线元素"直接决定：

  • 上三角矩阵 （主对角线下方元素全为 0 0 0）： ( a 11 a 12 ... a 1 n 0 a 22 ... a 2 n ⋮ ⋮ ⋱ ⋮ 0 0 ... a n n ) \begin{pmatrix} a_{11} & a_{12} & \dots & a_{1n} \\ 0 & a_{22} & \dots & a_{2n} \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & a_{nn} \end{pmatrix} a110⋮0a12a22⋮0......⋱...a1na2n⋮ann ；
  • 下三角矩阵 （主对角线上方元素全为 0 0 0）： ( a 11 0 ... 0 a 21 a 22 ... 0 ⋮ ⋮ ⋱ ⋮ a n 1 a n 2 ... a n n ) \begin{pmatrix} a_{11} & 0 & \dots & 0 \\ a_{21} & a_{22} & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n1} & a_{n2} & \dots & a_{nn} \end{pmatrix} a11a21⋮an10a22⋮an2......⋱...00⋮ann ；
  • 秩的计算规则 ：三角矩阵的秩等于主对角线上非零元素的个数。
    （原因：三角矩阵的行列式为"主对角线元素乘积"，最高阶非零子式的阶数由非零对角元素的个数决定）。

示例 ：上三角矩阵 A = ( 2 3 5 0 0 4 0 0 − 1 ) A = \begin{pmatrix} 2 & 3 & 5 \\ 0 & 0 & 4 \\ 0 & 0 & -1 \end{pmatrix} A= 20030054−1 ，主对角线元素为 2 , 0 , − 1 2, 0, -1 2,0,−1，非零个数为 2 2 2，故 R ( A ) = 2 R(A) = 2 R(A)=2。

（二）对角矩阵

对角矩阵是特殊的三角矩阵（主对角线外元素全为 0 0 0），形式为： ( a 11 0 ... 0 0 a 22 ... 0 ⋮ ⋮ ⋱ ⋮ 0 0 ... a n n ) \begin{pmatrix} a_{11} & 0 & \dots & 0 \\ 0 & a_{22} & \dots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \dots & a_{nn} \end{pmatrix} a110⋮00a22⋮0......⋱...00⋮ann ；

  • 秩的计算规则：对角矩阵的秩等于对角线上非零元素的个数（与三角矩阵规则一致，因对角矩阵同时属于上三角矩阵和下三角矩阵）。

示例 ：对角矩阵 B = ( − 3 0 0 0 0 0 0 0 5 ) B = \begin{pmatrix} -3 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 5 \end{pmatrix} B= −300000005 ，对角线上非零元素为 − 3 -3 −3 和 5 5 5，共 2 2 2 个，故 R ( B ) = 2 R(B) = 2 R(B)=2。

七、MATLAB 计算矩阵秩的代码实现

在 MATLAB 中，可直接使用内置函数 rank() 快速计算矩阵的秩，其底层通过奇异值分解（SVD）实现，能有效避免数值误差对结果的影响。以下为具体实现步骤与示例：

matlab 复制代码 
% 1. 定义矩阵 A（以 3×3 矩阵为例）
A = [1 2 3; 4 5 6; 7 8 9];

% 2. 计算矩阵 A 的秩
rank_A = rank(A);

% 3. 显示结果
disp(['矩阵 A 的秩为: ', num2str(rank_A)]);

运行结果：矩阵 A 的秩为: 2（与通过初等变换手动计算的结果一致）。

说明：

  • rank() 函数的逻辑是：对矩阵进行奇异值分解，得到奇异值后，将小于某个阈值（默认约为 1 0 − 15 10^{-15} 10−15）的奇异值视为 0 0 0，非零奇异值的个数即为矩阵的秩；
  • 阈值可通过函数参数调整，例如 rank(A, tol) 中 tol 为自定义阈值，适用于对数值精度有特殊要求的场景；
  • 该函数适用于任意维度的矩阵（包括非方阵），是工程计算中高效可靠的秩计算工具。

八、例题解析：矩阵秩的应用

（一）题目

已知行简化行阶梯形矩阵 A = ( 1 2 0 4 0 0 1 3 0 0 0 0 ) A = \begin{pmatrix} 1 & 2 & 0 & 4 \\ 0 & 0 & 1 & 3 \\ 0 & 0 & 0 & 0 \end{pmatrix} A= 100200010430 ，完成以下任务：

  1. 求 A A A 的秩；
  2. 求 A A A 的行秩并验证其与秩的关系；
  3. 求 A A A 的列秩并验证其与秩的关系。

（二）解答过程

1. 求矩阵 A A A 的秩

根据"行阶梯形矩阵的秩等于非零行的行数"这一结论：

  • 矩阵 A A A 中，非零行包括第 1 行 ( 1 2 0 4 ) \begin{pmatrix} 1 & 2 & 0 & 4 \end{pmatrix} (1204) 和第 2 行 ( 0 0 1 3 ) \begin{pmatrix} 0 & 0 & 1 & 3 \end{pmatrix} (0013)，共 2 2 2 行；
  • 零行仅第 3 行 ( 0 0 0 0 ) \begin{pmatrix} 0 & 0 & 0 & 0 \end{pmatrix} (0000)，且位于所有非零行下方（符合行阶梯形结构）。

因此， R ( A ) = 2 R(A) = 2 R(A)=2。

2. 求矩阵 A A A 的行秩

矩阵 A A A 的行向量组为：
α 1 = ( 1 , 2 , 0 , 4 ) , α 2 = ( 0 , 0 , 1 , 3 ) , α 3 = ( 0 , 0 , 0 , 0 ) \alpha_1 = (1, 2, 0, 4),\ \alpha_2 = (0, 0, 1, 3),\ \alpha_3 = (0, 0, 0, 0) α1=(1,2,0,4), α2=(0,0,1,3), α3=(0,0,0,0)

行秩是"行向量组中线性无关的最大向量个数"，分析如下：

  • 线性无关性验证 ：假设存在常数 k 1 , k 2 k_1, k_2 k1,k2 使得 k 1 α 1 + k 2 α 2 = 0 k_1\alpha_1 + k_2\alpha_2 = \boldsymbol{0} k1α1+k2α2=0（零向量），展开得：
    ( k 1 , 2 k 1 , k 2 , 4 k 1 + 3 k 2 ) = ( 0 , 0 , 0 , 0 ) (k_1, 2k_1, k_2, 4k_1 + 3k_2) = (0, 0, 0, 0) (k1,2k1,k2,4k1+3k2)=(0,0,0,0)
    解得 k 1 = 0 k_1 = 0 k1=0 且 k 2 = 0 k_2 = 0 k2=0，故 α 1 , α 2 \alpha_1, \alpha_2 α1,α2 线性无关；
  • 最大性验证 ：零向量 α 3 \alpha_3 α3 可由 α 1 , α 2 \alpha_1, \alpha_2 α1,α2 线性表示（ α 3 = 0 ⋅ α 1 + 0 ⋅ α 2 \alpha_3 = 0 \cdot \alpha_1 + 0 \cdot \alpha_2 α3=0⋅α1+0⋅α2），因此行向量组中线性无关的最大向量个数为 2 2 2。

因此， A A A 的行秩为 2 2 2，且 R ( A ) = 行秩 R(A) = \text{行秩} R(A)=行秩。

3. 求矩阵 A A A 的列秩

矩阵 A A A 的列向量组为：
β 1 = ( 1 0 0 ) , β 2 = ( 2 0 0 ) , β 3 = ( 0 1 0 ) , β 4 = ( 4 3 0 ) \beta_1 = \begin{pmatrix} 1 \\ 0 \\ 0 \end{pmatrix},\ \beta_2 = \begin{pmatrix} 2 \\ 0 \\ 0 \end{pmatrix},\ \beta_3 = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix},\ \beta_4 = \begin{pmatrix} 4 \\ 3 \\ 0 \end{pmatrix} β1= 100 , β2= 200 , β3= 010 , β4= 430

列秩是"列向量组中线性无关的最大向量个数"，分析如下（选取主元列 β 1 , β 3 \beta_1, \beta_3 β1,β3 验证）：

  • 线性无关性验证 ：假设存在常数 l 1 , l 3 l_1, l_3 l1,l3 使得 l 1 β 1 + l 3 β 3 = 0 l_1\beta_1 + l_3\beta_3 = \boldsymbol{0} l1β1+l3β3=0（零向量），展开得：
    ( l 1 l 3 0 ) = ( 0 0 0 ) \begin{pmatrix} l_1 \\ l_3 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} l1l30 = 000
    解得 l 1 = 0 l_1 = 0 l1=0 且 l 3 = 0 l_3 = 0 l3=0，故 β 1 , β 3 \beta_1, \beta_3 β1,β3 线性无关；
  • 最大性验证 ：非主元列可由主元列线性表示：
    • β 2 = 2 β 1 + 0 ⋅ β 3 \beta_2 = 2\beta_1 + 0 \cdot \beta_3 β2=2β1+0⋅β3， β 4 = 4 β 1 + 3 β 3 \beta_4 = 4\beta_1 + 3\beta_3 β4=4β1+3β3，因此列向量组中线性无关的最大向量个数为 2 2 2。

因此， A A A 的列秩为 2 2 2，且 R ( A ) = 列秩 = 行秩 R(A) = \text{列秩} = \text{行秩} R(A)=列秩=行秩。

（三）结论

通过例题验证，矩阵的秩、行秩与列秩三者完全相等，这一性质是矩阵理论的重要结论，也是理解矩阵结构与向量组关系的关键。

九、总结

矩阵的秩是线性代数中刻画矩阵"本质维度"的重要概念，其定义基于子式的非零性，计算可通过子式判别法或更高效的初等变换法实现。矩阵的秩具有诸多重要性质，如转置不变性、乘积秩的有界性等，这些性质为分析矩阵关系提供了有力工具。

在应用层面，矩阵的秩决定了线性方程组解的存在性与唯一性，可判断向量组的线性相关性，验证矩阵的可逆性，同时在数据降维、信息压缩等领域有广泛应用。掌握矩阵秩的概念、计算方法与应用场景，是学好线性代数的重要基础。

从两个角度看矩阵和向量相乘

Limi @_zhihu

前提条件

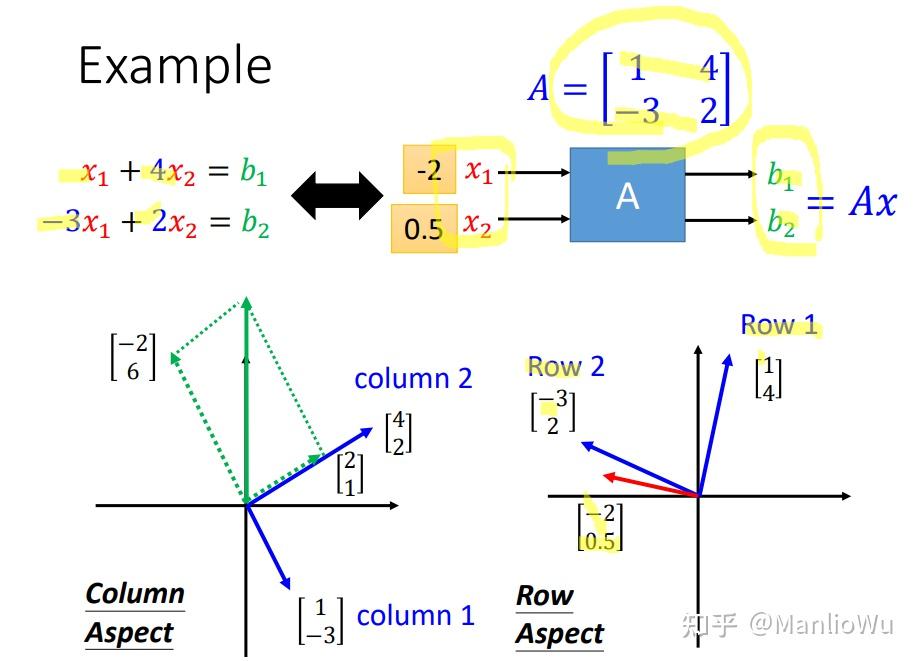
设矩阵 A A A 与向量 x x x 进行乘法运算，结果为向量 b b b，其维度与 x x x 相同。进行此乘法运算的前提条件是矩阵 A A A 的列数等于向量 x x x 的行数。以下从两个方面探讨如何求得 b b b ：行视角（Row Aspect）和列视角（Column Aspect）。

行视角（Row Aspect）

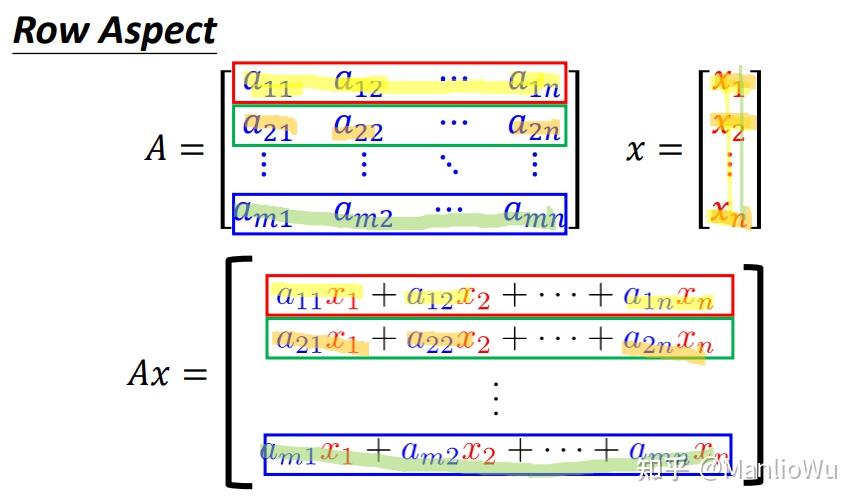
将矩阵 A A A 视作"行向量的堆叠"，即 A A A 的每一行均为一个向量。则向量 b b b 的第 i i i 个维度的值为 A A A 的第 i i i 行向量与 x x x 作内积的结果，即 b i = ( A i , x ) b_i = (A_i, x) bi=(Ai,x) 。内积运算要求两个向量的维度相同，这也解释了矩阵与向量相乘时矩阵列数与向量行数需相等的原因。此外，在矩阵 × \times × 矩阵的运算中，常采用的计算方法为：矩阵 A A A 的第 i i i 行与矩阵 B B B 的第 j j j 列相乘，结果为 C i , j C_{i,j} Ci,j 。矩阵 × \times × 向量可视为矩阵 × \times × 矩阵的特殊情形，即右侧矩阵仅有一列。

列视角（Column Aspect）

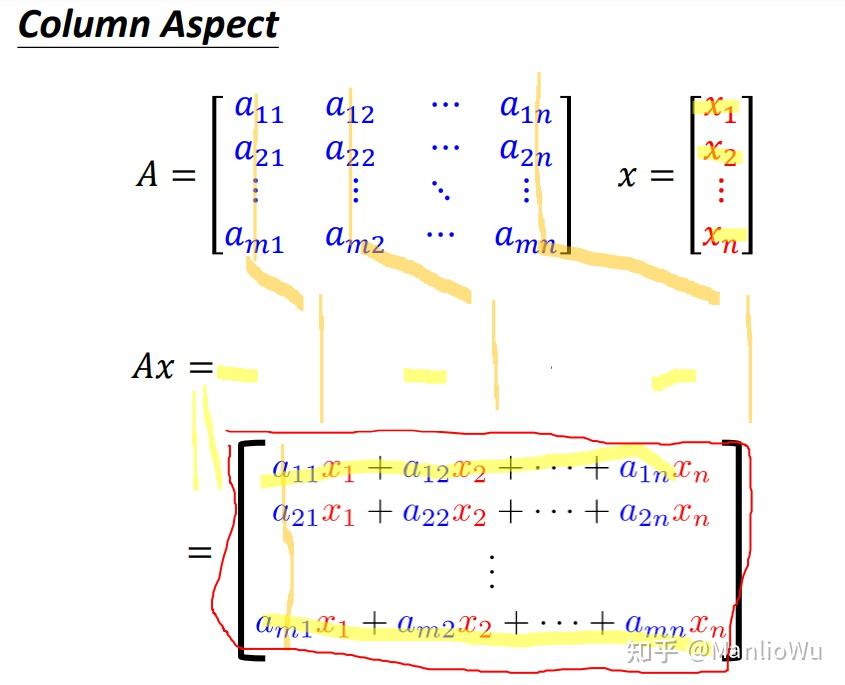
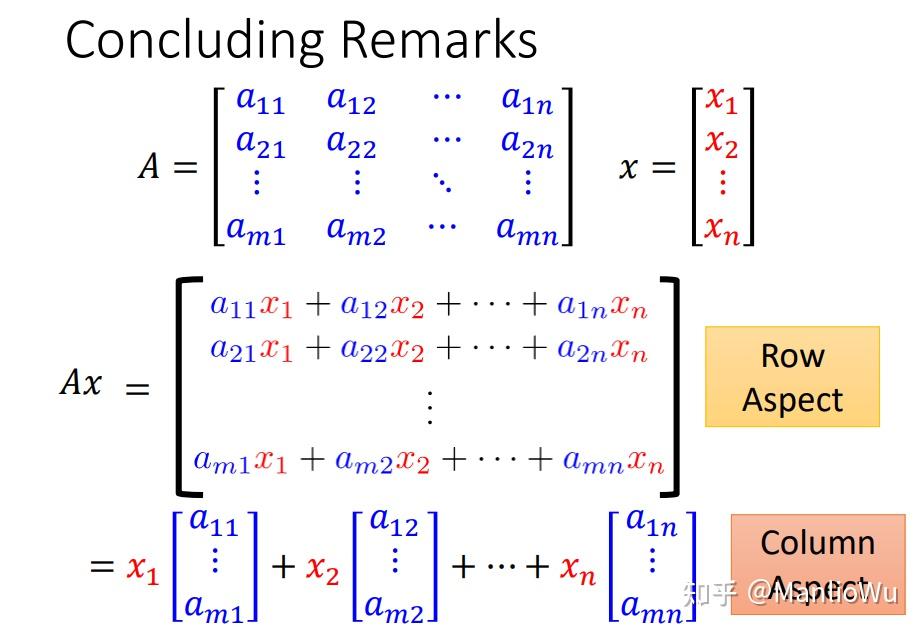
将矩阵 A A A 视作"列向量的并列"，即每一列均为一个向量。以向量 x x x 的第 i i i 个元素乘以矩阵 A A A 的第 i i i 个列向量，可得到 n n n 个向量（若矩阵 A A A 有 n n n 列）。将这 n n n 个向量相加，即得结果 b b b ，表达式为

b = ∑ i = 1 n A i ∗ x i b = \sum_{i=1}^{n} A_i \ast x_i b=i=1∑nAi∗xi

其中， A i A_i Ai 为列向量， x i x_i xi 为标量。此方法同样解释了矩阵列数与向量行数需相等的原因。该方法可视为对矩阵 A A A 的 n n n 个向量进行线性组合以得到新向量，在某些情况下更易于理解。在 3b1b 的线性代数课程中，有一种解释是将 A A A 的每个列向量视为向量空间的基向量，向量 x x x 的每个值为对应基向量的投影长度。将每个投影长度与基向量相乘后再求和，即可得到新向量。

总结与对比

综合来看，列视角（Column Aspect）在理解矩阵与向量相乘方面更具优势，具有重要的现实意义。

发布于 2022-08-04 17:14・广东

矩阵的秩以及行秩 = 列秩的原因

Limi @_zhihu

在矩阵理论中，矩阵的秩是一个重要概念，广泛应用于多个数学分支。矩阵的秩定义为矩阵中线性无关行向量或列向量的最大数目。具体来说，矩阵 A A A 的列秩是其线性无关列向量的最大数目，而行秩是其线性无关行向量的最大数目。这两个定义是等价的，即矩阵的秩等于其行秩也等于其列秩。

用数学符号表示，矩阵 A A A 的秩通常记作 r ( A ) r(A) r(A)、 rk ( A ) \text{rk}(A) rk(A) 或 rank A \text{rank}\ A rank A。矩阵的秩反映了矩阵中线性无关向量的最大数量，这一数量决定了矩阵的"厚度"或"维度"。

对于矩阵 A m × n A_{m \times n} Am×n，可以将其视为由 n n n 个列向量组成的矩阵。每个列向量对应一个基底，因此极大线性无关组的列向量个数（矩阵的秩）也称为列空间（Column Space）的维度。

在求解矩阵的秩时，通常通过基本行变换将其转换为阶梯矩阵。在阶梯矩阵中，每一行的第一个非零元素的列数依次向右移动（全零行除外）。即第 i + 1 i + 1 i+1 行的第一个非零元素位于第 i i i 行第一个非零元素的右下方。矩阵的秩 r r r 等于阶梯矩阵中单位向量（unit vector）的个数。单位向量是指向量中只有一个元素为 1，其余元素均为 0，也称为基向量（pivot column）或标准向量（standard vector），类似于 one-hot 编码。例如， [ 1 , 0 , 0 ] [1, 0, 0] [1,0,0] 和 [ 0 , 1 , 0 ] [0, 1, 0] [0,1,0] 均为单位向量。

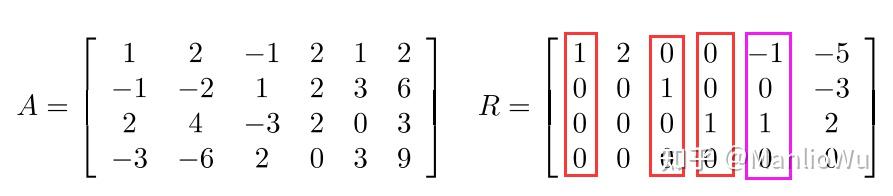
如图所示，左侧为原始矩阵，右侧为阶梯矩阵。阶梯矩阵中有 3 个单位向量（红色框标记），因此列秩为 3。紫色向量为何不能计入矩阵的极大线性无关组呢？因为其非零元素出现的位置并非对应行的第一个，即在其左侧存在单位向量，该向量可由其左侧的单位向量线性表示。例如，图中的矩阵 [ − 1 , 0 , 1 , 0 ] = − 1 × [ 1 , 0 , 0 , 0 ] + 0 × [ 0 , 1 , 0 , 0 ] + 1 × [ 0 , 0 , 1 , 0 ] [-1, 0, 1, 0] = -1 \times [1, 0, 0, 0] + 0 \times [0, 1, 0, 0] + 1 \times [0, 0, 1, 0] [−1,0,1,0]=−1×[1,0,0,0]+0×[0,1,0,0]+1×[0,0,1,0]。线性无关向量组中的向量不能相互表示，因此紫色向量不能计入。

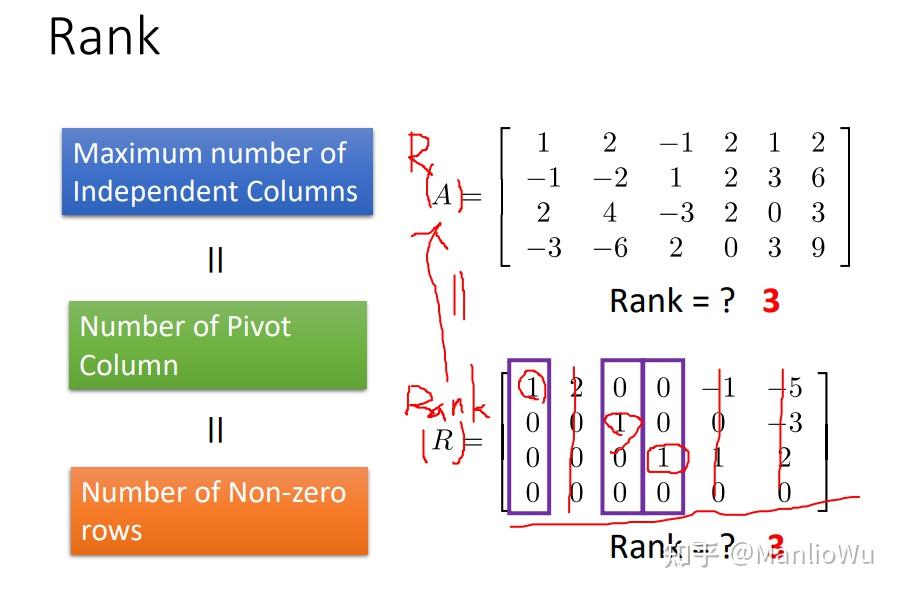
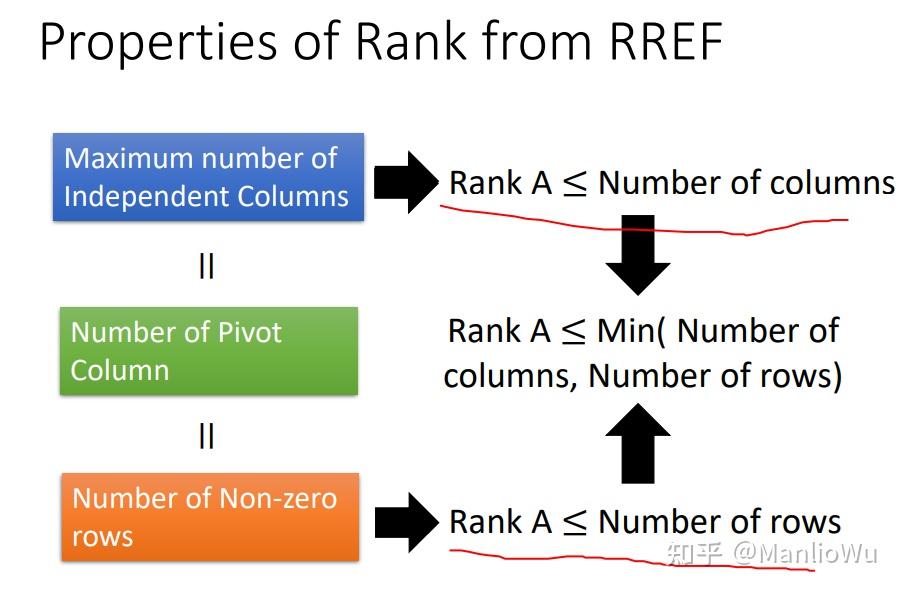
通过上述例子可知，单位向量的特点是：该向量中 1 的位置是其所在行的第一个非零元素。阶梯矩阵中单位向量的个数即为矩阵的秩。进一步分析可得，"第一个出现的非零元素" 的个数等于非零行的行数，即行秩。因此，矩阵的行秩等于列秩。此外，还可得出 rank ( A ) ≤ min ⁡ { m , n } \text{rank}(A) \leq \min\{m, n\} rank(A)≤min{m,n}。

总结如下图：

三种典型的子空间

列空间（Column Space）与行空间（Row Space）与零空间（Null Space）

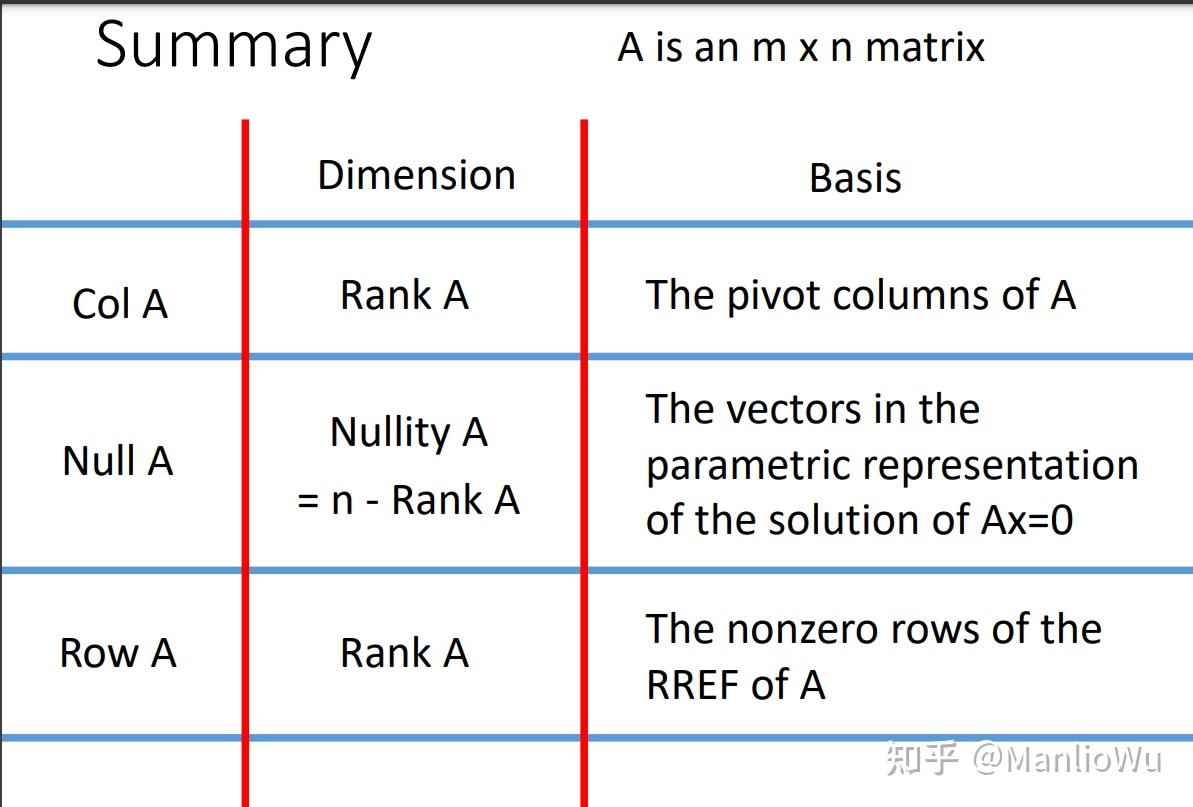
对于零空间（Null Space），即 A x = 0 Ax = 0 Ax=0 的基础解系构成的空间。以下是一个例子，其中存在 2 个自由变量（free variable），可得两个基向量（basis），因此零空间的维度为 2。矩阵的秩为 3，满足 rank ( A ) + dimension ( Null space ) = n \text{rank}(A) + \text{dimension}(\text{Null space}) = n rank(A)+dimension(Null space)=n。

具体分析如下：共有 n n n 个变量，其中 k k k 个为自由变量，其余 n − k n - k n−k 个变量可直接确定。在由 k k k 个自由变量构成的 k k k 维空间中，任取一个向量，再与 n − k n - k n−k 个确定的值组合，即可得到 A x = 0 Ax = 0 Ax=0 的解。从另一个角度理解，存在 k k k 个自由变量，是因为在阶梯矩阵中，有 k k k 个列向量可由其余 n − k n - k n−k 个基向量（pivot columns）线性表示。因此，给定一组 n − k n - k n−k 个值，即可求得一组 k k k 个值。综合所有情况，可形成一个 k k k 维空间。

单位向量（unit vector）的重要作用

单位向量是指向量中仅有一个位置为 1，其余位置均为 0。对于 n n n 维向量，存在 n n n 个单位向量。按"1" 的位置从小到大排序，分别为 e 1 , e 2 , e 3 , ... , e n e_1, e_2, e_3, \dots, e_n e1,e2,e3,...,en。其中， e 1 = [ 1 , 0 , 0 , ... , 0 ] T e_1 = [1, 0, 0, \dots, 0]^T e1=[1,0,0,...,0]T， e 2 = [ 0 , 1 , 0 , ... , 0 ] e_2 = [0, 1, 0, \dots, 0] e2=[0,1,0,...,0]， ... \dots ...， e n = [ 0 , 0 , 0 , ... , 1 ] T e_n = [0, 0, 0, \dots, 1]^T en=[0,0,0,...,1]T。

利用这些单位向量可"提取矩阵"。具体而言， A e i A e_i Aei 得到的向量是矩阵 A A A 的第 i i i 列。以下是一个示例：

0 1 − 1 0 \] \[ 1 0 \] = \[ 0 − 1 \] \[ 0 1 − 1 0 \] \[ 0 1 \] = \[ 1 0 \] \\begin{bmatrix} 0 \& 1 \\\\-1 \& 0 \\end{bmatrix} \\begin{bmatrix} 1 \\\\0 \\end{bmatrix}= \\begin{bmatrix} 0 \\\\-1 \\end{bmatrix} \\quad \\begin{bmatrix} 0 \& 1 \\\\-1 \& 0 \\end{bmatrix} \\begin{bmatrix} 0 \\\\1 \\end{bmatrix}= \\begin{bmatrix} 1 \\\\0 \\end{bmatrix} \[0−110\]\[10\]=\[0−1\]\[0−110\]\[01\]=\[10

矩阵与向量相乘可视为向量与其对应投影长度的乘积。单位向量 e i e_i ei 仅在第 i i i 个位置为 1，其余位置为 0，因此只有矩阵 A A A 的第 i i i 个列向量的投影长度为 1，其余投影长度为 0，从而可提取矩阵 A A A 的第 i i i 列。

编辑于 2022-08-07 20:16

线性代数 ------ 矩阵的列秩和行秩

原创于 2019-09-04 19:20:42 发布

1. 矩阵的列秩和行秩及秩的关系（行秩 = 列秩 = 秩）

2. 初等行变换不改变矩阵的线性相关性

3. 任一矩阵的秩、行秩和列秩相等

4. 求矩阵列向量组的秩及最大无关组示例

via:

热门推荐
01GitHub 镜像站点02UV 工具安装与国内镜像源配置指南03UV安装并设置国内源0446个Nano-banana 精选提示词，持续更新中05A股预测还能更准？开源大模型Kronos带你跑通预测+回测全流程06KGG转MP3工具|非KGM文件|解密音频07解决 WSL Ubuntu 中 /etc/resolv.conf 自动重置问题08Claude Code 平替：OpenAI发布 Codex CLI ，GPT-5 国内直接使用09conda中设置镜像地址（附所有可换的地址）10保姆级教程：手把手教你用Dify实现完美多轮对话（附Chatflow和提示词）