吴恩达深度学习课程一：神经网络和深度学习 第二周：神经网络基础（五）

此分类用于记录吴恩达深度学习课程的学习笔记。

课程相关信息链接如下：

1. 原课程视频链接：[双语字幕]吴恩达深度学习deeplearning.ai
2. github课程资料，含课件与笔记:吴恩达深度学习教学资料
3. 课程配套练习（中英）与答案：吴恩达深度学习课后习题与答案

本篇为第一课第二周，是2.11到2.13部分的笔记内容。

可能会发现跳过了几节，实际上是因为课程中的顺序为讲解结构后再分别讲解基础的顺序，笔记为了便于理解，便改为先讲解基础后可以顺畅的理解结构的顺序。跳过的节数在之前已讲到，或在之后再讲到。

---

本周的课程以逻辑回归为例详细介绍了神经网络的运行，传播等过程，其中涉及大量机器学习的基础知识和部分数学原理，如没有一定的相关基础，理解会较为困难。

因为，笔记并不直接复述视频原理，而是从基础开始，尽可能地创造一个较为丝滑的理解过程。

首先，经过之前第四部分内容的学习，我们了解了逻辑回归的传播过程，本篇将用一个问题将理论引入实操，进行后续内容的讲解。

现在我们已经知道了逻辑回归运行的完整过程，而在代码化这个算法的过程中，我们会发现在训练过程中至少需要两次遍历，一次遍历所有样本，一次遍历样本的所有特征，这就会形成一个双层嵌套的for循环，而这还仅仅只是一次迭代过程。

回忆最开始的深度学习简介部分，我们也知道深度学习的发展得益于数据规模的增加，而面对成千上万，甚至在大模型中数以亿计的样本，双重for循环带来的时间复杂度无疑太高了。

而如何在深度学习的代码中取消显式for循环遍历的逻辑，提升时间效率，就是本篇所讲的内容：向量化

我们以此开始本篇笔记的内容。

1.向量化

1.1 什么是向量化？

先看概念：

在深度学习中，"向量化"通常指的是将数据和计算从标量（逐个处理的方式）转化为向量（同时处理多个元素的方式），从而加速计算过程和提升效率。

用一个比较通俗的比喻来类比一下非向量化和向量化的区别：

想象一下你正在一个餐厅里做服务员，你需要为每一桌顾客端菜。

1. 非向量化：你一个一个地给顾客送菜。你先把第一桌的菜送过去，再回到厨房拿第二桌的菜，然后再送给第二桌，以此类推。每次送菜，你都要走来走去，浪费很多时间。
2. 向量化：现在想象你可以一次性拿好多盘菜，并且一次性把它们送到所有的顾客桌上。你不需要每次走来走去，而是一次性搞定多个任务。你把所有菜拿到手，再分别放到每一桌上，这样大大节省了时间和体力。

在向量化的基础上，我们可以再细分一下：

1. 数据输入的向量化 ：在传统的计算中，我们可能会逐个处理数据的每个元素（比如使用for循环），而在向量化过程中，我们将数据组织为向量或矩阵，并利用并行计算来一次性处理多个数据点。例如，如果有一个列表，需要对每个元素进行加法操作，传统方法可能是逐个遍历，而向量化方法则是将整个列表直接转化为一个向量，然后在硬件上一次性进行加法运算。
2. 计算输出的向量化 ：在深度学习中，很多操作可以通过矩阵和向量的线性代数运算 来实现，例如矩阵乘法、元素级加法、点积等。通过向量化，我们避免了逐步处理每个元素的方式，取而代之的是通过矩阵运算来并行计算。比如在神经网络的前向传播中，我们可以将输入数据与权重矩阵相乘，输出一个大的向量或矩阵，而不是逐个点积计算。

个人理解来说，向量化的本质其实是运用线性代数的数学理论对数据处理方式的优化。

1.2 直观感受向量化带来的效率提升

在实际代码编程中，我们并不需要像之前推公式一样来用代码实现向量化，在Python中，numpy库为我们提供了很多内置函数来进行向量化并取消显式的for循环。

现在我们复现一下课程中的例子，来感受向量化带来的效率提升。

import numpy as np #导入numpy库
import time #用于计时
a = np.random.rand(1000000) 
#生成一个包含 1000000 个元素的一维数组。所有的元素都是从 0 到 1 之间均匀分布的随机数。
#np.random 是 NumPy 中的一个子模块，专门用于生成随机数。
#rand 方法是 np.random 中的一个函数，用于生成均匀分布的随机数。
b = np.random.rand(1000000)
tic = time.time() #记录向量化运算开始时间
#time.time()用于记录此时系统时间的秒数表示
c = np.dot(a,b)#dot用于计算向量 a 和 b 的点积（内积)
# c = a1 * b1 + a2 * b2 + ... + a10000 * b10000
toc = time.time()#记录向量化结束时间
print(f'向量化计算的运行时间：{1000*(toc-tic)}毫秒')

如注释里所说，本段代码便用dot()函数来实现了两个一百万维度的矩阵的点积运算，我们并没有显式的 使用for循环来遍历两个矩阵中的每一个元素。

其运行结果为：

我们再通过非向量化，即使用for循环的方式来一遍这个过程，就能发现二者在效率上的显著差别。

代码如下：

import numpy as np #导入numpy库
import time #用于计时
a = np.random.rand(1000000) 
b = np.random.rand(1000000)
c = 0
tic = time.time() 
for i in range(1000000):
    c+=a[i]*b[i]
toc = time.time()#
print(f'非向量化计算的运行时间：{1000*(toc-tic)}毫秒')

很显然，这种方式是对两个矩阵的元素挨个相乘再相加，就像我们比喻里的一道一道上菜。

来看一下结果：

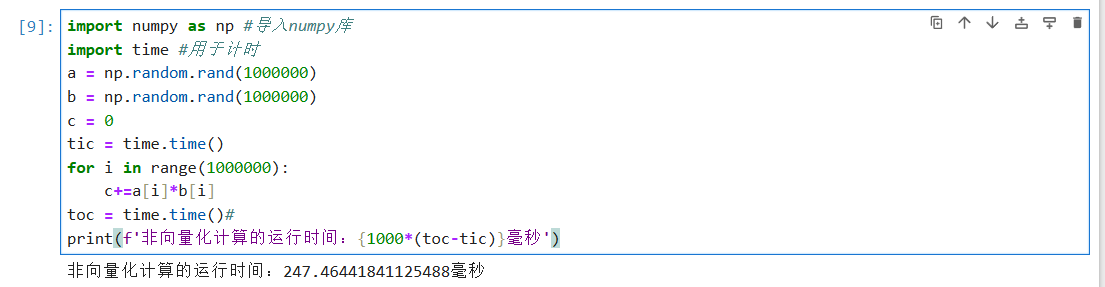
非向量化的运行时间是向量化的两百多倍 ，这便是向量化带来的效率提升。

我们再补充一下课程里提及的其他例子：

import numpy as np #导入numpy库
# 1.计算指数
a = np.random.rand(1000000) 
c = np.exp(a)  # exp用于计算数组a中每个元素的指数（e的幂）
# c = e^a1, e^a2, ..., e^a10000 按照这个格式计算

# 2.计算对数
d = np.log(a)  # log用于计算数组a中每个元素的自然对数（以e为底）
# d = ln(a1), ln(a2), ..., ln(a10000) 按照这个格式计算

# 3.计算绝对值
f = np.abs(a)  # abs用于计算数组a中每个元素的绝对值
# f = |a1|, |a2|, ..., |a10000| 按照这个格式计算

# 4.计算元素最大值
e = np.maximum(a, 0.5)  # maximum用于计算数组a中每个元素与0.5的最大值
# e = max(a1, 0.5), max(a2, 0.5), ..., max(a10000, 0.5) 按照这个格式计算

这些内置函数都可以替代相应的显式for循环，因此，在编程中，尽可能地使用向量化而避免显式的for循环便是优化效率的一条准则，每当我们想使用for循环时，可以先思考是否可以通过numpy的内置函数来替代它。

1.3 numpy库是如何提高效率的？

作为理论部分，我们也简单总结一下这部分，了解即可：

1. NumPy 中的向量化 （vectorization）是将一组运算转化为在整个数组上同时进行的操作，而不是使用显式的 Python for 循环。这种方式大大减少了 Python 循环的开销。
2. NumPy 提供了广播机制，这使得形状不同的数组可以进行运算，广播机制自动调整数组的形状，以适应运算。广播大大减少了内存占用，并且避免了不必要的复制，优化了运算速度。
3. NumPy 底层利用了现代 CPU 的并行计算能力。通过在 CPU 内部实现 SIMD 指令集（单指令多数据流），NumPy 可以在多个数据元素上并行执行相同的操作，从而加速计算过程。

而广播机制我们也会在之后讲到。

2.逻辑回归的向量化

现在我们把向量化引入逻辑回归，最终可以实现，这里我们仅讲解理论，而完整代码会在本周的课后作业里实现。

2.1 正向传播的向量化

先回忆一下，逻辑回归的正向传播是从输入进行线性组合得到加权和，再经过激活函数得到输出的过程，而在一次迭代中，如有 \(m\) 个样本，就要计算 \(m\) 次这样的过程。

我们先看一下课程中的相关符号表示：

而简单来说，正向传播的向量化便是所有输入都放在一个矩阵里进行并行计算得到各自的加权和，再并行通过激活函数得到输出。

其实这一部分在本周的第二部分的符号表示部分已经有所提及，我们现在系统化的再梳理一遍：

如果我们希望不在正向传播的计算过程中显示的使用for循环，那就要进行下面的向量化处理：

1. 定义向量 \(\mathbf{x}\) ，向量 \(\mathbf{x}\) 是一个 \(n\) 维的列向量， \(n\) 即为输入的特征数量，\(\mathbf{x}\)即代表一个样本的所有输入特征，表示为：

\[\mathbf{x} = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} \]

2. 定义一个矩阵 \(X\) 来表示容纳所有 \(\mathbf{x}\) ，大小为\(n*m\)，\(m\)为样本数量，\(X\) 即代表所有样本的输入特征，其表示为：

\[\mathbf{X} = \begin{bmatrix} \vdots & \vdots & \vdots & \cdots & \vdots \\ x^{(1)} & x^{(2)} & x^{(3)} & \cdots & x^{(m)} \\ \vdots & \vdots & \vdots & \cdots & \vdots \end{bmatrix} \]

3. 使用权重矩阵 \(w\) 来表示每个特征的权重 ，大小为\(n*1\) ,表示为：

\[\mathbf{w} = \begin{bmatrix} w_1 \\ w_2 \\ \vdots \\ w_n \end{bmatrix}\]

4. 定义偏置向量\(b\)（实际因广播机制不用进行这一步，这里先阐述向量化原理，我们后面再展开) ,\(b\) 实际上是将同一个值扩展到 \(m\) 维，大小为\(1*m\) 来配合 \(m\) 个样本的加权和计算，其表示为：

\[\mathbf{b} = \begin{bmatrix} b_1 & b_2 & \cdots & b_m \end{bmatrix} \]

5. 定义向量 \(Z\) ,其大小为\(1*m\) ，其中每一个元素 \(z\) 便代表一个样本在该次迭代中的线性加权和 ，\(Z\) 即是所有样本在该次迭代中的加权和，表示为：

\[\mathbf{Z} = \mathbf{w}^T \mathbf{X} + \mathbf{b} \]

再细化一下：

\[\mathbf{Z} = \begin{bmatrix} z_1 & z_2 & \cdots & z_m \end{bmatrix} 其中，\mathbf{z^{(i)}} = \mathbf{w}^T \mathbf{x^{(i)}} + \mathbf{b} \]

6. 最后，我们定义向量\(A\) ,其大小同样为\(1*m\) ，其中每一个元素\(a\)便代表一个 \(z\) 经过激活函数得到的输出 ，表示为： $$\mathbf{A} = \begin{bmatrix}
   a_1 & a_2 & \cdots & a_m
   \end{bmatrix}$$
   经过这样的方式，我们便通过向量化的方式进行了正向传播得到所有样本在一次迭代的输出，避免了使用显式的for循环来依次遍历每一个样本的输出。

其实这里本想直接续上反向传播中对梯度计算的向量化，但由于涉及到使用之前跳过的链式法则对梯度的简化运算，还是放在了下一篇按链式法则-反向传播-广播机制的顺序统一讲解。