2025 诺贝尔物理学奖 | 从宏观量子隧穿到量子计算

斐夷所非2025-10-13 9:45

注：本文为 "2025 诺贝尔物理学奖 | 宏观量子隧穿" 相关合辑。

不同文章有相似段落重复，略作重排，未整理去重，忽略相同看差异。

如有内容异常，请看原文。

2025 诺贝尔物理学奖解读：他们是超导量子比特实验的开端

原创 施郁 墨子沙龙 2025 年 10 月 07 日 18:52 上海

作者 | 施郁编辑 | 墨子沙龙

瑞典皇家科学院于北京时间 2025 年 10 月 7 日宣布，将 2025 年诺贝尔物理学奖授予约翰·克拉克（John Clarke）、米歇尔·德沃雷（Michel H. Devoret）与约翰·马丁尼斯（John M. Martinis），以表彰他们"在电路中实现宏观量子隧穿与能级量子化（for the discovery of macroscopic quantum mechanical tunnelling and energy quantisation in an electric circuit）"的杰出贡献。

为什么今年诺贝尔物理学奖会颁布给这三位科学家？他们的工作涉及什么方面？又有哪些应用？本文将介绍这个领域的科学背景和发展历程，从中看到这三位科学家的贡献。

超导和超流

超导和超流经常被称作"宏观量子现象"。但是通常情况下，它们只是微观量子行为的宏观表现，并不是宏观变量的量子化。

超导悬浮

液氦超流

按照统计性质，量子粒子分为两种。一种叫做玻色子，可以处于相同状态。另一种叫做费米子，任何两个费米子都不能处于相同状态。在量子力学中，同种粒子，比如两个电子或者两个光子，是绝对完全一样的，叫做全同粒子。由 2 个质子和 1 个中子组成的原子核叫做氦 3 原子核，它与 2 个电子组成电中性的氦 3 原子，是费米子。由 2 个质子和 2 个中子组成的原子核叫做氦 4 原子核，它与 2 个电子组成电中性的氦 4 原子，是玻色子。

因此在系统总能量最低时，简单来说（忽略相互作用），大量的全同玻色子都处在相同的最低能量状态，叫做玻色-爱因斯坦凝聚。超流就是玻色-爱因斯坦凝聚的后果。最常见的超流是氦 4 超流。

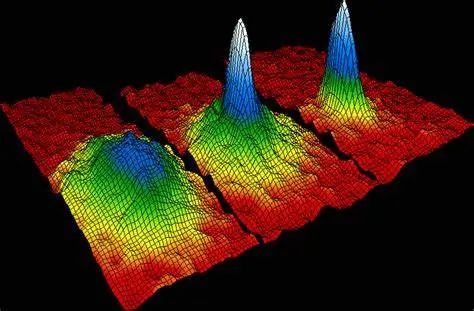
玻色-爱因斯坦凝聚

而费米子可以由某种机制导致两两配对，形成"库珀对"，近似于玻色子。库珀对的近似玻色-爱因斯坦凝聚也导致超流。最常见的费米子超流是固体中的电子超流，一般称作超导电性（因为电子带电），简称超导。也存在电中性的费米子超流，如氦 3 的超流。

库珀对卡通示意图

基于库珀对凝聚的超导理论于 1956 年由巴丁（John Bardeen），库珀（Leon Cooper）和施里弗（John Robert Schrieffer）提出，库珀对的总自旋（内禀角动量）为 0。而氦 3 超流的库珀对总自旋为 1。对氦 3 超流的理论做出贡献的莱格特（Anthony J. Leggett）因此获得 2003 年诺贝尔物理学奖。安德森（Philip Anderson）等人对此也有重要贡献。

玻色-爱因斯坦凝聚、超流或者超导都可以由一个序参量描写，有时被称为宏观波函数，它是一个复数函数。粒子之间作用力比较弱时，可以用平均场理论来描述，假设所有全同粒子的波函数一样，它们相乘在一起，就构成系统的整体波函数。每个全同粒子的单体波函数就是序参量（通常再乘以粒子数的平方根）。对于相互作用较强的情况，序参量是规范对称自发破缺所导致的场算符的期望值，或者是单玻色子或者双费米子约化密度矩阵的最大本征值的本征函数（这个说法对应于 Penrose-Onsager 和杨振宁的非对角长程序）。

不管理论上以何种方式得到，这个序参量（或称宏观波函数）的一个重要特征是相位。相位随着位置的变化驱动了超流。约瑟夫森效应体现了这个相位的物理真实性。对于由绝缘体薄层隔开的两个超导体，两个超导体的宏观波函数的相位差直接导致穿过绝缘体的超导电流，电流强度正比于相位差的正弦函数，这就是约瑟夫森效应。它是剑桥大学研究生约瑟夫森（Brian Josephson）在学习 Philip Anderson 的超导课程时，用多体微观理论得到的结论。宏观波函数的相位差是一个宏观变量，但是由于粒子数涨落很大，相位成为一个经典变量。

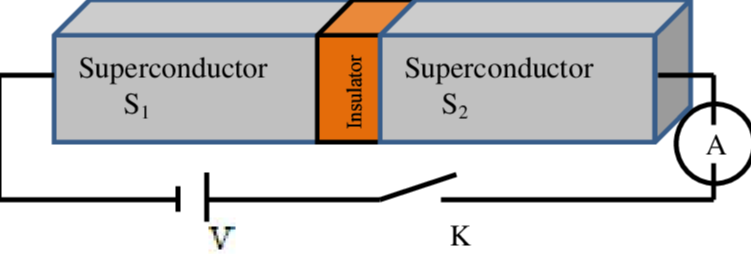
约瑟夫森结

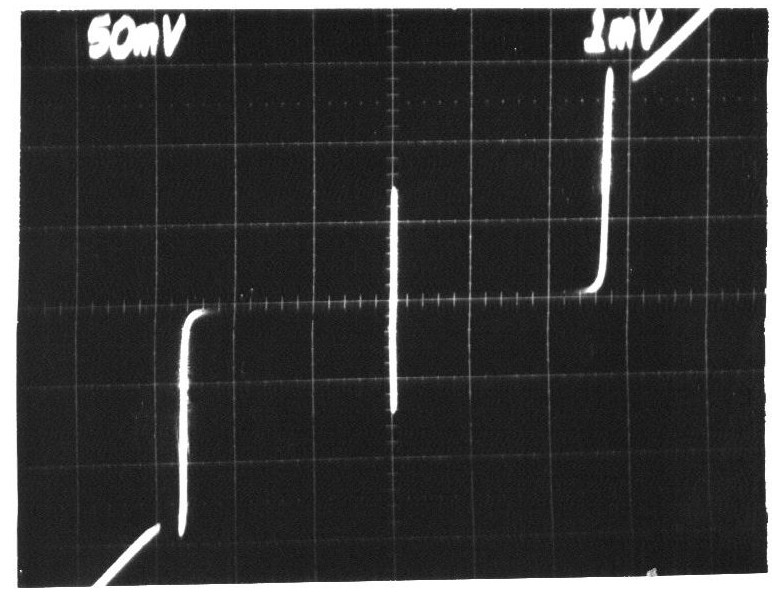
约瑟夫森结的 I-V 曲线

粒子数与相位是量子共轭算符

对于小约瑟夫森结，相位也有涨落，粒子数与相位都成为量子力学算符，而且它们具有共轭关系，类似位置和动量之间的关系，也就是互不对易（改变作用顺序，结果不同）。这也使得它们之间也服从海森堡的不确定关系。

1980 年，Leggett 指出[1]，通常所谓的"宏观量子系统"，即超导和超流，以及磁通量子化和约瑟夫森效应这些后果，并没有表明量子力学原理适用于宏观系统，因为其中并没有宏观上的不同状态之间的量子叠加（如假想的薛定谔猫），但是由于在超导或超流状态下，耗散低，超导器件特别是 SQUID（超导量子干涉仪，即具有两个约瑟夫森结的超导环），通过特别的设计，适合于寻找不同宏观状态之间的量子叠加或量子隧穿。这引领了几十年约瑟夫森结的量子效应的研究，包括超导量子比特的兴起。

作者与 Leggett 教授（摄于 2003 年 10 月诺贝尔奖宣布后伊利诺伊大学立即为 Leggett 举行的庆祝会）

约瑟夫森结量子行为的首次实验观察

1985 年，加州大学伯克利分校 John Clark 教授带领两位学生 John Martinis 和 Michel Devoret，首先观察到偏电流约瑟夫森结的量子行为[2]。偏电流是指外电流。具体来说，他们观察到量子化的能级，表明了约瑟夫森结的相位差确实是一个量子力学算符，实验结果与理论一致。

描述这个系统的方程类似于一个质点的一维运动，约瑟夫森结相位差对应于质点位置。对应后，质点所受的势能作为位置的函数，是倾斜的余弦函数。在约瑟夫森结中，这个倾斜由偏电流引起。约瑟夫森结的零电压态对应于质点的势能低点（叫做势阱）。量子力学预言，在势阱中，质点处于所谓束缚态（指束缚在势阱中），而且所能具有的能量是分立的，叫做能级------也就是说，只有某些特定的数值才被允许，这叫能量量子化。原子中的电子就具有这个性质。具有如此能级结构的人工器件有时被称作人造原子，可以用约瑟夫森结实现，也可以用半导体量子点实现。

Clarke 和两位学生将约瑟夫森结用微波辐照，发现当微波频率（乘以普朗克常数）等于分立能级之差时（几个 GHz），"质点"逃逸率（逃逸出势阱的概率）大大增加，也就是说，约瑟夫森结两端的电压以及导致的电流大大增强。这是一种共振，类似于，如果电磁波的频率（乘以普朗克常数）与原子中的电子能级差相等，低能级的电子就会吸收光子，跃迁到高能级。他们观测到，随着温度升高，逃逸率从量子共振激发过渡到经典热激发。

就这样，约瑟夫森结的量子行为首次得到证明，而且表明可以通过电路对它进行控制，并能将多个约瑟夫森结连结起来。短短两年后，Clark 因此获得了低温物理的菲列兹·伦敦奖（Fritz London Memorial Prize）。

他们的约瑟夫森结材料是 Nb-NbOx-PbIn，中间的氧化铌是绝缘体，两边的铌和铅铟合金是超导体。后来人们改用 Al-Al2O3-Al, 即铝-氧化铝-铝，它的耗散更低[3]。

小约瑟夫森结

约瑟夫森结的能量来自两个互相竞争的部分。一是库珀对带来的充电能，等于充电能常数（一对库珀对的充电能）乘以库珀对数目（减去一个所谓的门电荷数）的平方。另一个是约瑟夫森隧道耦合能，是库珀对隧穿导致的负能量（当库珀对波函数是隧道两边的叠加态时，能量降低），等于负的约瑟夫森能量常数（临界电流乘以磁通量子，除以 2π）乘以相位差的余弦。

1990 年代，很多研究组研究小约瑟夫森结[4]。代尔夫特工业大学的 J. E. Mooij 组研究了约瑟夫森结阵列[5]，哈佛大学的 Tinkham 组观察到超导单电子晶体管的电流-电压关系中的 2e 周期性[6]，当时在法国 Saclay 原子能委员会的 Devoret 组也证实了这个结果[7]，J. E. Mooij 组证明了相位与电荷（库珀对数目乘以电子电荷）之间的海森堡关系[8]。

量子计算的兴起

1980 年代，量子计算的研究开始出现。1990 年代早期，Peter Shor 提出可以有效解决因子化问题的量子算法，使得量子计算得到更广泛的关注。当时，量子计算的物理实现主要在光子、离子、原子这些系统中研究，而固体物理系统被认为太复杂，自由度太多。1990 年代后期，研究超导约瑟夫森结和半导体量子点的科学家开始对量子计算感兴趣，试图实现量子比特。当时仍然有很多科学家不知道这个领域。记得世纪之交时，笔者向一位知名凝聚态理论学者说起对凝聚态系统中的量子纠缠与量子计算实现有点兴趣，对方不知道什么意思。

固态"人造原子"有其优点，它可以借由电路实现仔细的调控，因为相对于真正的原子，更容易调控各种参数，而且也容易和传统的技术整合，便于扩展到很多量子比特。

任何用来实现量子计算的物理系统，首先要解决的问题是量子比特的物理实现，包括单个量子比特以及不同量子比特的耦合。下文主要回顾单个超导量子比特的实现。

超导量子比特

超导量子比特有很多种。当充电能比约瑟夫森能大很多时，相位涨落大，库珀对数目接近明确，所实现的量子比特叫做电荷量子比特，又叫库珀对盒子。当约瑟夫森能比充电能大很多时，粒子数涨落大，相位明确，所实现的量子比特叫做相位量子比特，也可实现磁通量子比特。另外还有 quantronium, transmon, flxonium，等等。

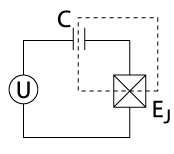
电荷量子比特

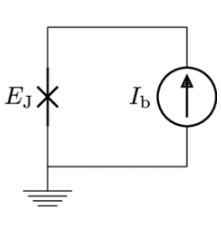
相位量子比特

1998 年，Devoret 组证明了电荷量子比特叠加态的存在性[9]。

1999 年，当时在日本 NEC 实验室的中村泰信及其合作者 Pashkin 和 Tsai 实现了电荷量子比特的叠加态[10]。他们用电压脉冲，实现了相差一对库珀对的两个粒子数本征态的量子叠加。虽然相干时间（维持叠加态的时间）只有 2 纳秒，但是脉冲时间只有 100 皮秒。后来，他们又实现了在微波作用下，这两个电荷本征态之间的拉比振荡[11]。

2000 年，纽约州立大学石溪分校的 Lukens 组[12] 和代尔夫特的 Mooij 组[13] 分别在特别设计的、包含 3 个约瑟夫森结的超导环中，实现了不同电流方向（顺时针和逆时针）的量子叠加态。这也叫磁通量子比特，因为两个方向的电流对应不同的、穿过环路的磁通量。但是量子叠加的证据是间接的，来自光谱[14]。

2002 年，在 Saclay 和耶鲁大学的 Devoret 组用围绕一个库珀对盒子巧妙设计的超导电路，以哈密顿量的两个本征态作为量子比特，实现了任意幺正演化（包括拉比振荡）以及投影测量[15]。他们自己称这个量子比特为 quantronium。这是电荷-磁通混合量子比特[14]，自由演化时，对电荷和磁通噪声都不敏感，等效于电荷量子比特，而读出时又改变控制参数，对磁通敏感，等效于磁通量子比特。

与之同时，堪萨斯大学的韩思远组发表了偏电流约瑟夫森结的两个本征态之间的拉比振荡[16]。当时在科罗拉多的 NIST 的 Martinis 组也观察到同样的现象。偏电流约瑟夫森结也就是 1985 年 Clarke、Martinis 和 Devoret 最初研究的系统，它的两个本征态对磁通噪声敏感度低于磁通量子比特[14]。它们被称为相位量子比特[18,19]，因为约瑟夫森能比充电能大很多。

2003 年，Mooij 组实现了磁通量子比特的拉比振荡和读出[20]。当时中村泰信在该组访问，是该工作的合作者。

后来这个领域又取得了长足的进展，包括双量子比特和多量子比特的耦合，直到最近用几十个量子比特实现量子优越性[21,22]。这里不再赘述。

置于微波腔中的超导量子电路还导致所谓电路量子电动力学，电磁波显示出量子行为。比起基于腔量子电动力学（原子与光子耦合）的量子门和读出，基于电路量子电动力学的量子门和读出快 1000 倍，但是退相干也快 1000 倍，不过电路量子电动力学能获得大量数据[3]。

Leggett 一直在推动用 SQUID 检验是否存在宏观不同的状态的量子叠加[23]。最近的一个磁通量子比特实验说明，至少对于 10 纳秒、170 纳安培的电流，存在两个方向电流状态的量子叠加[24]。

小结

通过我们的回顾综述，可以看到，J. Clarke 和他的学生 J.M.Martinis 和 M.H. Devoret 最早通过偏电流约瑟夫森结，首次观察到约瑟夫森结的量子行为。后来 Devoret 又做了一系列工作，包括 1998 年证明了电荷量子比特叠加态的存在性， 2002 年实现电荷-磁通混合量子比特的拉比共振和其他演化及投影测量。中村泰信 1999 年和 2001 年分别首先实现超导量子比特的量子叠加和拉比振荡，是在电荷量子比特中。他 2003 年还参与 Mooij 组实现了磁通量子比特的拉比振荡和读出。

2025 年诺贝尔物理学奖官方解读：宏观尺度下的量子特性

诺奖小分队 中科院物理所

2025 年 10 月 07 日 19:45 北京

2025 年诺贝尔物理学奖得主约翰·克拉克（John Clarke） 、米歇尔·德沃雷特（Michel H. Devoret） 、约翰·马丁尼斯（John M. Martinis） 通过一系列实验证明，量子世界的奇异特性可以在像是手掌那么大的一个宏观系统中具象体现出来。他们的超导电路系统能够实现不同量子态之间的隧穿，犹如穿墙而过般突破经典限制；同时他们精准验证了这个系统仅能够以特定数值大小吸收和释放能量，完全符合量子力学的理论预测。

2025 年诺贝尔物理学奖获得者

一系列突破性实验

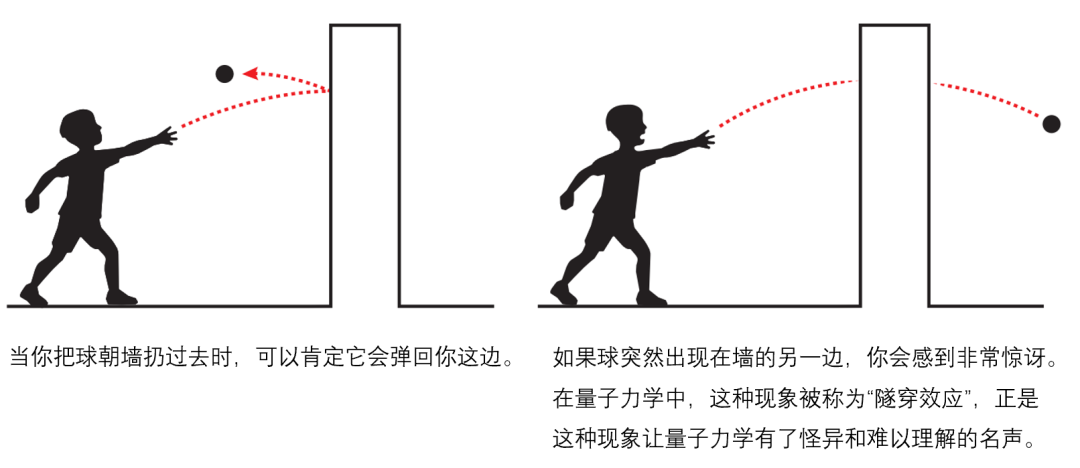
量子力学所描述的特性在单粒子尺度上尤为显著 。在量子物理学中，这些现象被称为微观现象 ------即这个尺度要远小于光学显微镜所能观测的极限。与之相对的是宏观现象，宏观现象所研究的对象由大量的粒子构成。以我们日常接触过的球体为例：它由大量的围观分子组成，因此不会体现出宏观的量子力学效应。我们知道，当球被掷向墙壁时每次都会弹回。然而在微观世界中，单个粒子有时却能径直穿过等效屏障出现在另一侧 。这种量子力学现象被称为量子隧穿效应。

今年的诺贝尔物理学奖表彰了展示量子隧穿效应如何在宏观尺度上被观测到的实验，这些实验涉及多个粒子。1984 年和 1985 年，约翰·克拉克，米歇尔·德沃雷特和约翰·马丁尼斯加州大学伯克利分校进行了一系列实验。他们构建了一个由两个超导体组成的电路，超导体是一种能够无电阻传导电流的材料。他们用一层根本不导电的薄材料将这两个超导体隔开。在该实验中，他们展示了能够控制和研究一种现象，即超导体中的所有带电粒子的行为一致，就好像它们是一个充满整个电路的单一粒子。

这个类似粒子的系统被困在一个没有电压却有电流流动状态中------这个状态中的能量不足以让带电粒子逃脱。在实验中，该系统展现出量子特性，通过隧穿效应逃离零电压状态从而产生电压 。诺贝尔奖得主们还证明了该系统是量子化的，也就是说它只能吸收或释放特定量值的能量。

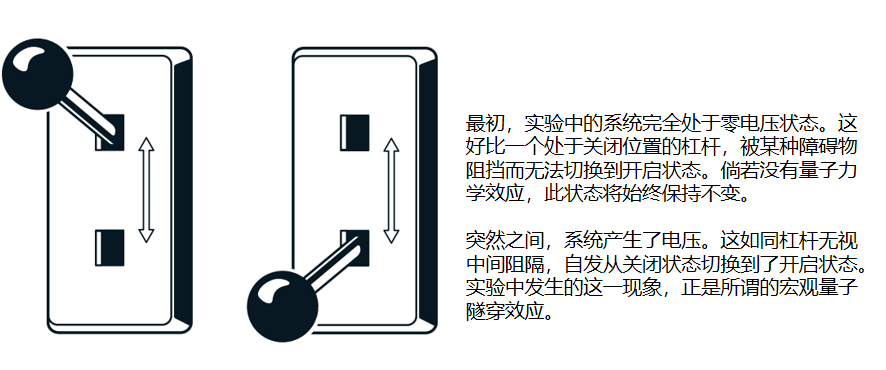
*隧穿与跨越*

为了实现这一目标，获奖者们数十年来不断发展理论概念与实验工具。量子物理学与相对论共同构成了现代物理学的基础，一个世纪以来，研究人员们一直在探索其内涵。

大家已经熟知单个粒子可以发生隧穿。到 1928 年，物理学家乔治・伽莫夫（George Gamow）意识到，隧穿效应正是某些重原子核以特定方式发生衰变的原因。原子核内各种力的相互作用在其周围形成了一道势垒，将内部粒子束缚其中。然而，尽管存在这样的势垒，原子核的一小部分有时仍会分裂出来，移动到势垒之外并发生逃逸 ------ 留下一个已经转变为另一种元素的原子核。如果没有隧穿效应，此类核衰变就不可能发生。

隧穿是一种量子力学过程，其中，偶然性 发挥着重要作用。有些原子核的势垒又高又宽，导致其碎片突破势垒逸出需要耗费大量时间；另一些原子核的势垒则相对容易逸出，衰变过程也就更为迅速。如果只观察单个原子，我们无法预测这种情况何时会发生，但通过观察大量同种原子核的衰变，我们可以在隧穿发生前测量出预期时间 。描述这一现象最常用的方法是引入 "半衰期" 概念，即样本中半数原子核发生衰变所需的时间。

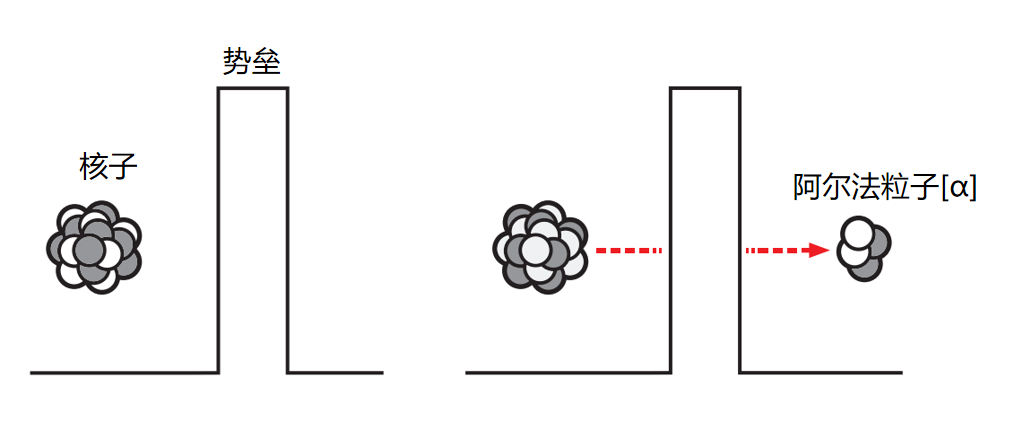
近一个世纪以来，物理学家们早已知晓：隧穿效应是某类核衰变（α 衰变)发生的必要条件。在这一过程中，原子核的一小块碎片会挣脱束缚，出现在原子核外部。

物理学家们很快便开始思考，是否有可能研究一种涉及多个粒子同时参与的隧穿现象。一种新式实验方法思路源自于某些材料在极低温下出现的现象。

在普通导电材料中，电流的流动是因为电子可以自由地在整个材料中移动。在某些材料中，单个电子在导体中穿行时可能会变得有序，形成一种同步的"舞蹈"，从而实现无阻力流动。此时，该材料变成了超导体，电子也成对结合。这些电子对被称为库珀对（Cooper Pairs） ，以利昂·库珀（Leon Cooper）的名字命名------他与约翰·巴丁（John Bardeen）和罗伯特·施里弗（Robert Schrieffer）共同详细阐述了超导体的工作原理（三人于 1972 年共同获得诺贝尔物理学奖）。

库珀对的行为方式与普通电子截然不同 。电子具有高度的独立性，彼此倾向于保持距离------如果两个电子具有相同的属性，它们就不能处于同一位置。这一点在原子中可以看到，例如电子会分布在不同的能级，即电子壳层中。然而，当超导体中的电子结成对时，它们就丧失了一部分个体性：两个独立的电子总是可以区分的，但两个库珀对却可以完全等同 。这意味着超导体中的库珀对可以被描述为一个单一的单元，一个量子力学系统。用量子力学的语言来说，它们被描述为一个单一的"波函数。这个波函数描述了在给定状态下观测到系统具有特定属性的概率。

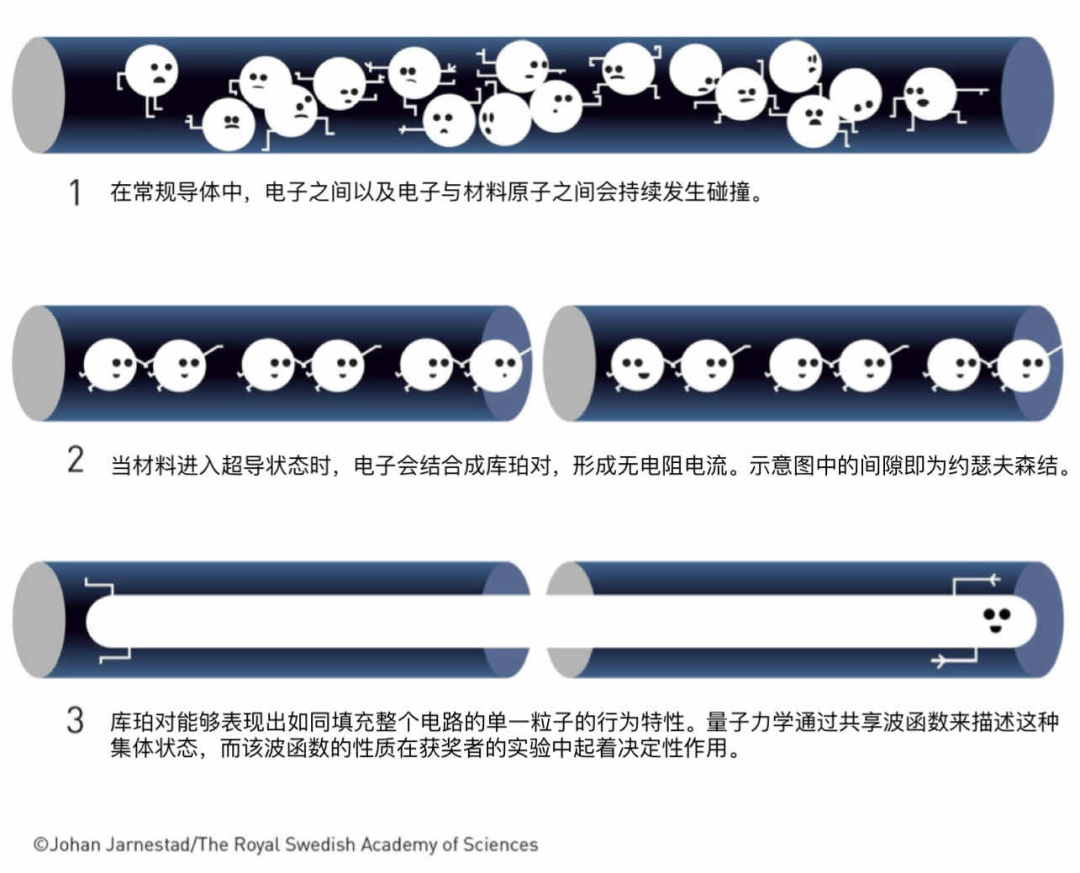
当两片超导体以薄绝缘层相隔连接时，便构成了约瑟夫森结。该器件以布赖恩·约瑟夫森（Brian Josephson）命名，他曾对该结构进行了量子力学计算。他发现当考虑结两侧波函数时会出现有趣的现象 (1973 年诺贝尔物理学奖)。约瑟夫森结很快获得实际应用，包括用于基本物理常数和磁场的精确测量。

该结构还为探索量子物理基本原理提供了新方法。安东尼·莱格特（Anthony Leggett ）(2003 年诺贝尔物理学奖得主) 就曾采用该方法，他在约瑟夫森结宏观量子隧穿方面的理论研究推动了新型实验的发展。

研究团队正式启动工作

这些课题与约翰·克拉克的研究兴趣高度契合。他当时是美国加州大学伯克利分校的教授，1968 年在英国剑桥大学获得博士学位后即赴该校任教。在伯克利期间，他组建研究团队，专注于利用超导体和约瑟夫森结探索一系列物理现象。

二十世纪八十年代中期，取得巴黎大学博士学位的米歇尔·德沃雷特（ Michel Devore）以博士后身份加入克拉克的研究团队。该团队还包括博士生约翰·马丁尼斯（ John Martinis）。**他们共同承担起了验证宏观量子隧穿现象的挑战性课题。需要极其谨慎精确地屏蔽实验装置可能受到的所有干扰因素。**他们成功优化并测量了电路的全部特性，从而实现了对系统的精细理解。

为测量量子现象，他们向约瑟夫森结输入微弱电流并测量与电路中电阻特性相关的电压 。约瑟夫森结两端的初始电压如预期显示为零。这是因为系统的波函数被束缚在阻止电压产生的量子态中。随后他们研究系统隧穿该量子态产生电压所需的时间。由于量子力学存在随机性要素，他们进行大量测量并将结果绘制成图表，从中读取零电压状态的持续时间。这种方法类似于通过统计大量衰变事例来测量原子核的半衰期。

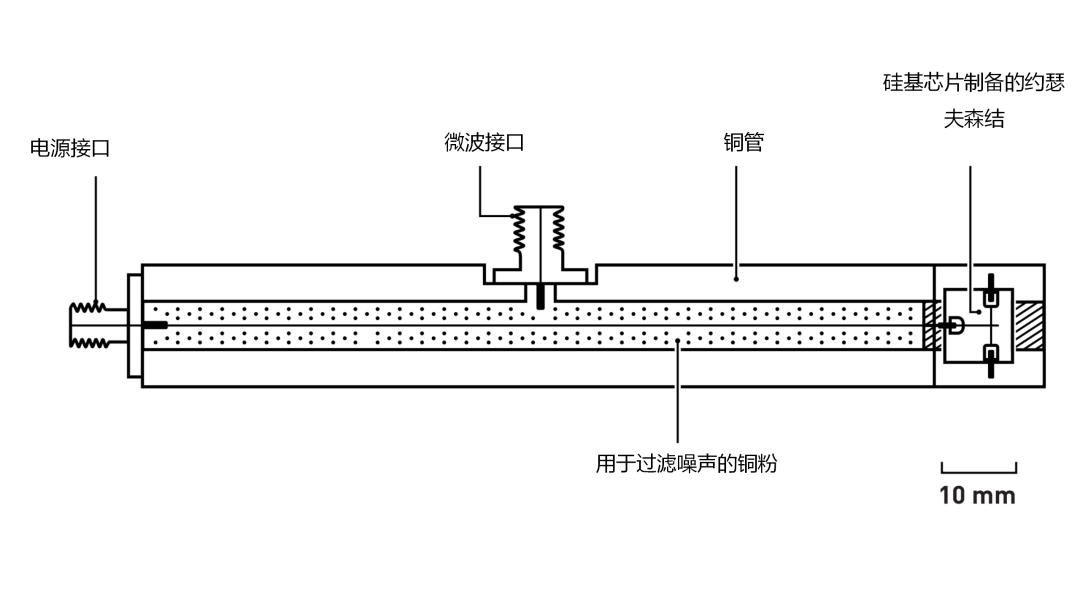
约翰·克拉克，米歇尔·德沃雷特（Michel H. Devoret）和约翰·马丁尼斯（John M. Martinis）使用超导电路构建了一套实验系统 。承载该电路的芯片尺寸约为一厘米见方。此前，隧穿效应和能量量子化现象仅在含有少量粒子的系统中被研究过。而在该实验中，这些现象出现在拥有数十亿库珀对的量子力学系统中，这些库珀对完全填满了芯片上的超导体。由此，该实验成功地将量子力学效应从微观尺度扩展到了宏观尺度。

隧穿效应展示了：实验装置中的库珀对如何在同步的"舞动"中，表现得就像一个单一的巨型粒子。当研究人员观察到该系统具有离散的能级结构时，他们进一步得到了这种行为的确证。"量子力学"这一名称的由来，正是因为在微观过程中的能量是被分割成一个个独立的"包"的------量子。三位获奖者将变化波长的微波注入到处于零电压态的系统中，他们发现：部分微波被系统吸收后，系统跃迁到了更高的能量状态。这表明：当系统所含能量增加时，其零电压态的持续时间会变短------这正与量子力学的预言一致。一个被势垒困住的微观粒子，其行为方式与这一宏观系统的表现如出一辙。

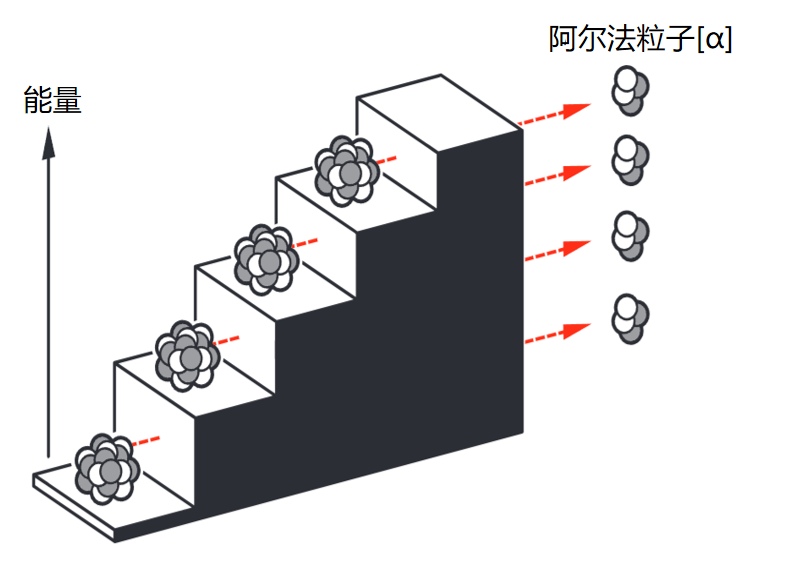
尽管势垒后的量子力学系统可能具有大范围的能量值，但只能吸收或发射特定量值的能量。该系统呈现量子化特征。由于高能级比低能级更容易发生隧穿现象，因此统计而言，高能态系统的量子态被束缚的时间低于低能态系统。

实践和理论意义

这项实验对于深化对量子力学的理解具有重要意义。其他类型的宏观尺度量子效应，往往是由大量微观个体的量子性质叠加而成的。例如激光器、超导体、超流体等宏观现象，都是由众多微观粒子的量子行为共同作用的结果。然而，这项实验与此不同------它直接从一个本身就是宏观的量子态（即由无数粒子组成的波函数）中，产生出一个可测量的宏观效应------可观测的电压。

理论物理学家安东尼·莱格特（Anthony Leggett）将这些获奖者创造的宏观量子体系，与著名的"薛定谔的猫"思想实验进行比较。在那个假想实验中，如果不打开盒子，猫既"活着"又"死去"。（薛定谔本人曾于 1933 年获得诺贝尔物理学奖。）薛定谔设想这个场景的目的，是为了揭示量子力学在宏观世界中看似荒谬的特性，因为量子效应通常会在宏观尺度上被"消解"。一个完整的猫体，其整体量子态是不可能在实验室中直接展示的。

然而，莱格特指出，由约翰·克拉克、米歇尔·德沃雷特以及约翰·马丁尼斯所进行的一系列实验表明，确实存在某些由大量粒子组成的系统，它们的整体行为仍严格遵循量子力学的规律。这种由大量库珀对构成的宏观系统，虽然比一只小猫要小上许多个数量级，但由于实验测量的是整个系统的量子性质，从量子物理学家的角度看，它与薛定谔的"猫"有着某种相似之处。

这种类型的宏观量子态，为研究微观粒子世界规律的实验开辟了新的可能。它可以被视为一种"大型人工原子"------一个带有导线与接口、能够接入实验装置、并可被应用于新型量子技术的"原子"。例如，这类"人工原子"可用于模拟其他量子体系，从而帮助我们理解它们的行为。

另一个例子是约翰·马丁尼斯随后进行的量子计算实验 ，他正是利用了他们三人此前所展示的能量量子化效应。在那个实验中，他使用具有量子化能级的电路，将其作为信息单元------量子比特（qubit）。最低能级与第一激发态分别代表逻辑"0"和"1"。超导电路正是当前构建未来量子计算机所探索的重要技术路线之一。

因此，今年的获奖者们不仅在物理实验室中带来了实际的研究工具与应用潜能，也为我们在理论上理解物理世界的本质提供了新的洞见。

Ref

编辑：诺奖小分队

2025 诺贝尔物理学奖深度解读：宏观量子隧穿的重大科学意义

李政道研究所 TDLI 2025 年 10 月 08 日 19:02 上海

北京时间 2025 年 10 月 7 日，瑞典皇家科学院宣布，将 2025 年度诺贝尔物理学奖授予：

  • 约翰·克拉克 (John Clarke)，加州大学伯克利分校

  • 米歇尔·H·德沃雷 (Michel H. Devoret)，耶鲁大学及加州大学圣巴巴拉分校

  • 约翰·M·马丁尼斯 (John M. Martinis)，加州大学圣巴巴拉分校

以表彰他们在**"电路中发现宏观量子隧穿与能量量子化"**方面的开创性贡献。

这项工作在实验上首次证实，由大量粒子构成的宏观系统可以整体展现出纯粹的量子力学行为，从而在根本上模糊了微观量子世界与宏观经典世界的界限，并为现代量子信息科学，特别是超导量子计算，奠定了实验基础。

一、量子隧穿效应：微观粒子的基本属性

在经典物理学框架下，一个粒子若想越过一个能量壁垒（势垒），其自身能量必须高于势垒的高度，否则将被完全阻挡。

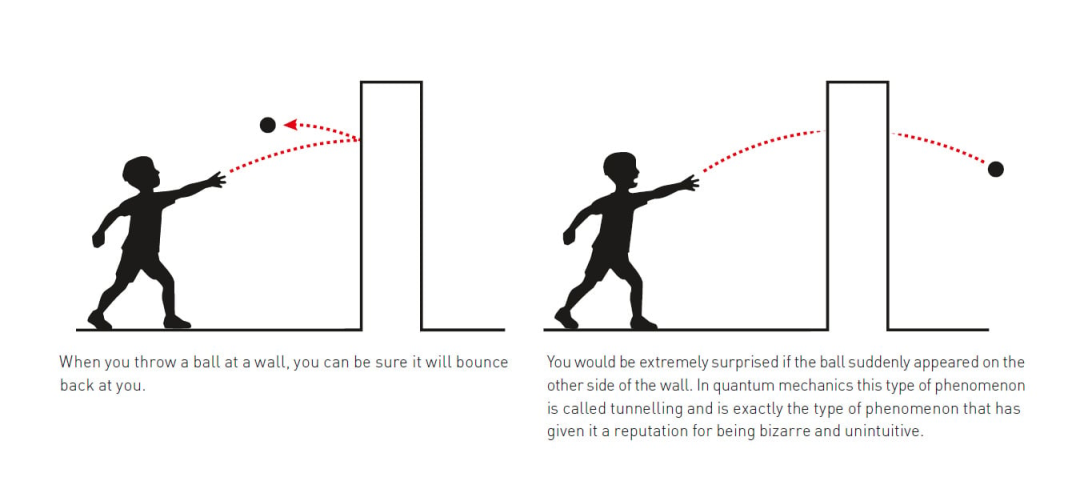
图 1 当你往一面墙上扔一颗球，在经典情况下（左）， 除非你扔出的球比墙壁高，否则可想而知小球会被弹回。而在量子力学中（右），小球却有一定的概率出现在墙的另一侧

然而，量子力学描绘了一幅截然不同的图景。根据量子理论，微观粒子（如电子）具有波粒二象性，其状态由波函数描述。**当粒子的波函数遇到势垒时，即便粒子能量低于势垒高度，其波函数依然能够渗透进壁垒并延伸至另一侧。**这意味着，粒子在势垒另一侧出现的概率并不为零。这种粒子在自身能量不足的情况下直接穿过势垒的现象，即为量子隧穿效应。

长期以来，"尺度"被认为是量子力学与经典力学之间严格的分界线。根据量子退相干理论，宏观系统由阿伏伽德罗常数量级的粒子构成，其与环境的相互作用（如热振动、粒子碰撞、电磁干扰）会快速破坏粒子间的量子相干性，导致系统表现出经典力学行为。因此，此前学界普遍认为：量子隧穿等量子效应是"微观粒子的专属属性"，宏观系统无法作为一个整体展现量子相干性------这一认知直至三位获奖者的实验才被打破。

二、宏观量子现象的实验验证

上世纪 80 年代，三位获奖者设计并完成了一系列里程碑式的实验，成功地在一个人造的宏观系统中观测到了量子效应。

他们的实验核心是一个基于**约瑟夫森结（Josephson junction）**的超导电路。该系统的关键特性在于，电路中所有库珀对（Cooper pairs）的集体行为，可以通过一个宏观的物理量来描述，例如通过约瑟夫森结的磁通量或结两端的相位差。这个宏观的集体自由度在特定条件下，其行为如同一个单一的量子粒子。

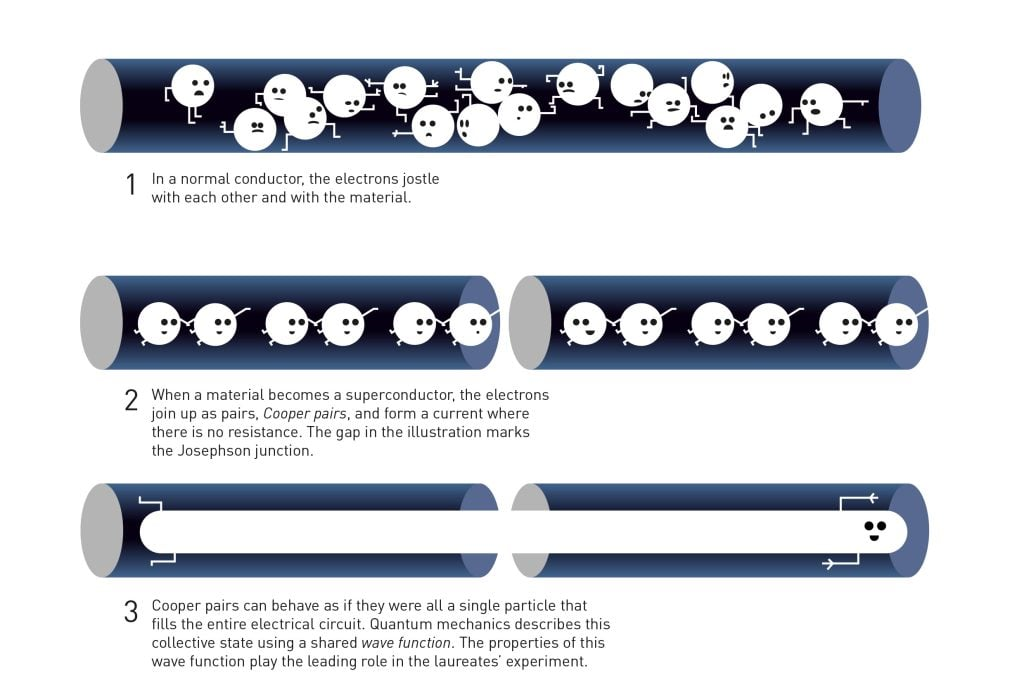
图 2 在普通导体中，电子之间以及电子与材料之间会相互碰撞。而当材料转变为超导体时，电子会结合成库珀对，形成无电阻电流。图示中的间隙标志着约瑟夫森结的形成。库珀对的行为模式如同一个填充整个电路的单一粒子。量子力学通过共享波函数来描述这种集体状态，而该波函数的特性在获奖者的实验中扮演着关键角色。©约翰·亚恩斯塔德/瑞典皇家科学院

该实验取得了两个关键性的成果：

1、宏观量子隧穿（Macroscopic Quantum Tunnelling, MQT）的直接观测：

实验中，这个宏观量子变量被束缚在一个由电路参数决定的势阱中，此状态对应于电路的零电压态。根据经典物理学，若没有足够大的外部扰动，系统将永远被困在该势阱内。然而，实验明确观测到，该系统能够以一定的概率自发地从这个亚稳态"隧穿"出去，跃迁到另一个状态。这一跃迁的实验信号，正是电路两端一个可被精确测量的、非零电压的出现。这首次为宏观量子隧穿的存在提供了无可辩驳的证据。

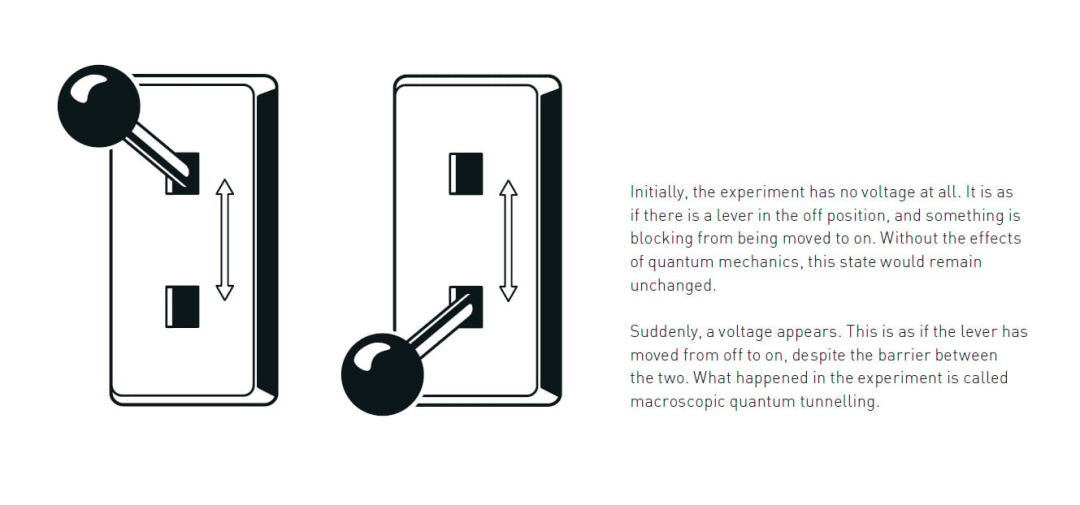
图 3 最初，实验中完全没有电压。这就好比有一个处于关闭位置的开关，有某种东西阻止它被移动到开启位置。如果没有量子力学的效应，这种状态将保持不变。突然，电压出现了。这就好像开关从关闭移动到了开启位置，尽管两者之间存在障碍。实验中发生的这种现象被称为宏观量子隧穿。

2、宏观系统能级的量子化验证：

通过施加微波场并观察系统的响应，他们进一步证明，这个宏观电路系统的能量并非任意连续值，而是呈现出一系列分立的、量子化的能级，与天然原子的能级结构高度相似。这证实了该宏观系统确实是一个可被调控的量子实体。

三、奠基性意义与前沿应用

今年正值量子力学诞生 100 周年。一直以来，量子隧穿效应作为经典力学与量子力学的重要差异而备受关注，三位获奖者通过实验成功打破了量子力学适用范围的尺度界限，在更广阔的范围上验证了量子力学的适用性。这项工作不仅是一次基础物理理论的深刻验证，更直接催生了全新的技术领域。

1、超导量子计算的基石："人工原子"

这项研究最重要的遗产，是证明了超导电路可以被设计成"人工原子"。这些人工原子可以拥有与天然原子一样的分立量子能级，并且可设计、可操作，可以用其最低的两个能级（基态和第一激发态）构成量子比特（Qubit）。由于其宏观尺寸，这些量子比特能够与外部的微波控制线路实现强耦合，从而进行高效的量子态初始化、操控和读取。

可以说，克拉克、德沃雷和马丁尼斯的工作，为整个超导量子计算领域铺平了道路，当今世界各大科技公司和研究机构所采用的主流超导量子计算方案，其物理基础均源于此。

"今年的诺奖有点特别，奖励的不只是这三位获奖者的研究发现，更是间接地对他们成果的工程化以及应用落地的奖励。"上海交通大学李政道研究所凝聚态物理研究部助理研究员应江华在接受文汇报记者采访时谈到，尤其是马蒂尼斯的得奖可以说明这一点，他可以说是"超导量子计算的工程化和应用落地的旗帜性人物。"

2、高精度量子传感器与新物理探测

不仅如此，宏观量子系统还为高精度物理探测开启了一扇新大门。宏观量子系统的状态，尤其是隧穿速率，对外界环境的微弱扰动极为敏感，这使其成为探索基础物理前沿的理想探针。

例如，某些理论预测的未知第五种力或轻量级暗物质粒子（如轴子），可能会与约瑟夫森结中的库珀对发生微弱耦合，从而轻微地改变其势垒参数。这种改变将导致宏观量子隧穿速率发生可测量的变化，为寻找新物理的实验信号提供了全新的途径。同样，这类极端敏感的量子系统也被提议用于探测其他基本物理效应，例如在微观尺度检验引力理论或探测引力波等。

2025 年诺贝尔物理学奖所表彰的成就，不仅在理论层面深化了我们对量子与经典边界的理解，更在实践层面为人类提供了构建和操控复杂量子系统的强大工具，其深远影响贯穿于当今的量子科技革命之中。从理论上"人工原子"的诞生，到现实中量子计算机的初现端倪，这项基础性的突破正如诺贝尔委员会所评价，"开启了一个量子计算、传感与加密的新纪元"。

文稿丨李所研会学术部 (林嘉督 黄惊涛) 应江华

编辑丨孟闻卓

责任编辑丨李姝姝

到底什么是宏观量子现象？一文助你搞懂 2025 年度诺贝尔物理学奖

原创 薛德堡 物含妙理 2025 年 10 月 12 日 13:30 广东

很多人对 2025 年度诺贝尔物理学奖感到困惑。

宏观量子现象不是早就被发现了吗？例如超流（Super Fluidity）（典型的如约瑟夫森结中的超导电流），既然如此，为什么物理诺奖委员会认为三位物理学家"发现了电路中的宏观量子力学隧穿与能量量子化"？

的确，超导电流本身是宏观量子现象的一个重要成果，但它只是量子规则在宏观世界创造的"静态秩序"。

而 2025 年诺奖所表彰的，是首次清晰地捕捉到了这个宏观系统本身"动态的量子灵魂"------它的整体状态像微观粒子一样，在进行典型的量子运动。 这为我们操控宏观量子态（即制造量子比特）打开了大门，直接引发了第二次量子革命。

如果你还不太明白，请跟本文来一起捋一遍这背后的奥秘。本人尽量用通俗的语言，相信你一定能搞懂。

01

一些预备知识

在我们熟悉的日常生活中，物理世界的运行是遵循牛顿力学的。

例如，将一个球抛向墙壁，它必然会反弹回来；处于光滑谷底的小球，若动能太小，它是无法逃离谷底的；物体的能量似乎可以平滑连续地变化，任意大小取值都可以存在。

然而，在微观粒子的世界里，支配一切的量子力学却展现出一套截然不同的法则，典型的有两个方面。

一方面，粒子可以像幽灵般穿越势垒，称为量子隧穿效应（quantum tunneling effect）。

另一方面，粒子的能量只能取某些离散的数值，即能量量子化（energy quantization）。

那么问题是，这些奇异的量子行为，是否只属于那个看不见的微观世界？当数以亿计的粒子组装成我们肉眼可见的宏观物体时，量子效应为何似乎消失无踪呢？

2025 年的诺贝尔物理学奖，正是授予了三位通过精巧实验正面回答了这一问题的科学家：约翰·克拉克、米歇尔·德沃雷和约翰·马丁尼斯。他们的工作首次无可辩驳地证明：宏观量子现象确实存在！

也就是说，在一个尺寸足以用指尖捏取、由数十亿粒子组成的宏观电路，就像微观粒子那样，整体上发生了隧穿效应，并具有能量量子化的特点。

要理解他们的突破，我们首先需要认识两种特殊的物理实体：超导体 （super conductivity）和约瑟夫森结（Josephson junction）。

在极低的温度下，某些材料会进入超导状态，其电阻会完全消失。电流可以在其中永无止境地流动而没有任何损耗。这背后的机理是，电子会两两结合成所谓的库珀对（cooper pair），库珀对的关键特性是，它们不是各自独立的粒子，而是会协同一致行动，形成一个整体的量子态。

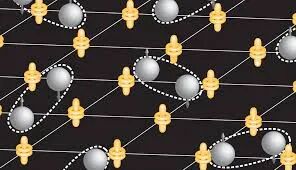
至于约瑟夫森结，就是由两块超导夹住一块绝缘材料构成的。通常情况下，两块超导体靠得非常近，中间仅用一层薄至纳米级别的绝缘体隔开，这就是一个典型的约瑟夫森结。

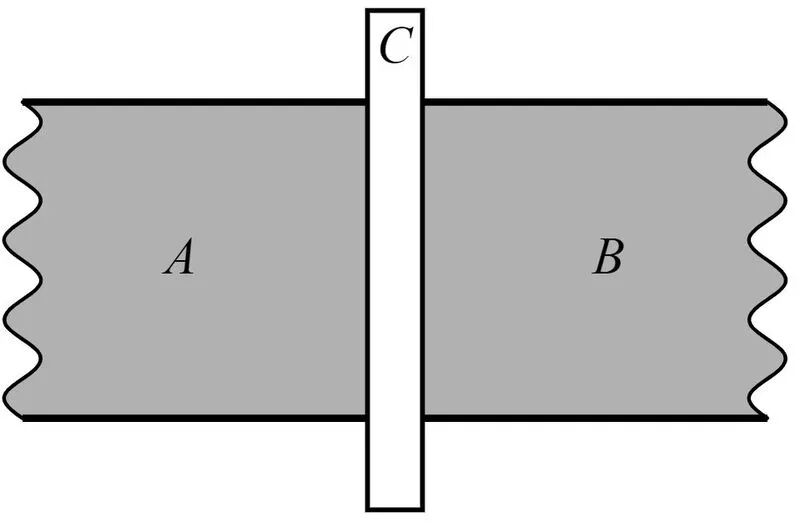
你可能觉得奇怪，超导既然这么爽滑，你却在它们中间夹一层绝缘体，这是想干啥呢？

这涉及一个重要的量子效应，即约瑟夫森效应（Josephson effect）------超导电流，也就是库帕对，能无损耗地通过夹在超导体中间的绝缘层。

理解这种量子效应，需要用到波函数 （wave function）和量子隧穿（Quantum tunneling）这两个核心概念。

在量子力学中，粒子是由波函数描述的。粒子不像经典的小球那样按照确定的轨迹运动，而是表现出波动性，即按不同的概率存在于空间各处，在某点的概率密度即为波函数在该点的模的平方。

这种粒子在空间分布的概率，就像疏密不同的云一样，云浓厚的地方，粒子出现的机会大，反之则机会少。

前苏联两位物理学家（曼德尔施塔姆和列昂托维奇) 于 1928 年发现，电子或原子等微观粒子能出现在被势能垒隔开的区域，此即量子隧穿效应。

如下图所示，虽然隧穿的概率较低，但是存在的，并且研究发现，随着能垒区域宽度减小，隧穿效应增强。

当粒子遇到一个非常薄的势垒（如约瑟夫森结中的绝缘层）时，它对应的波函数会指数衰减地渗入势垒内部。如果势垒足够薄，波函数的"尾巴"就能从势垒的另一侧显露出来。

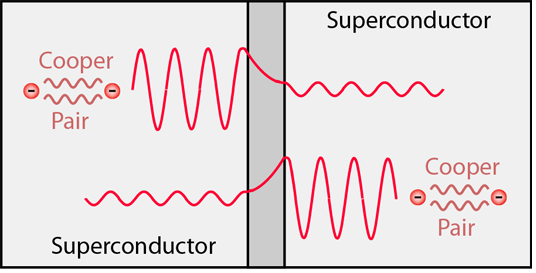
于是，左右两个超导体中库珀对的宏观波函数在绝缘层这个狭小空间内发生了重叠，可以形象地理解为它们"牵手"了，形成了一个跨越整个结的、统一的量子态，导致了跨越绝缘层的超导电流。

02

电路实验

有了以上预备知识，现在来看三位诺奖得主设计的电路实验。

首先，在超流电流低于某个临界值时，约瑟夫森结处于一个"零电压状态"------电路中有电流持续流动，但两端却测不到任何电压。

你可能觉得奇怪，怎么会有电流却没有电压呢？

前面说过，这个电流是一种超流现象。之所以说超流，因为它是以"量子隧穿"这种无损耗的方式流过的，而不是靠电压驱动的。电流是这个整体量子态的内禀属性，就像心跳是生命体的属性一样，它自然存在，无需电压驱动。

在这里，我们可用一个简单比喻来理解这个系统：想象一个放在绝对光滑的波浪形瓦楞板上的小球。这个瓦楞板是略微倾斜的，小球被困在瓦楞板的 U 形滑道底部。

在这个比喻中，小球的位置代表的是整个超导电路的一个集体性质------相位差，它决定了流过结的超流电流的大小。具体关系式为

在经典物理的图像里，如果小球没有获得足够的能量（比如被人推一把）来翻越旁边的波峰，它将永远被困在原地。

然而，克拉克、德沃雷和马丁尼斯的实验却揭示了一些截然不同的事情！

他们将包含约瑟夫森结的电路冷却到接近绝对零度，以排除任何热扰动的干扰。在如此极端的条件下，他们观察到：即使没有任何外部能量输入，电路两端的电压也会突然、随机地从零跃升到一个有限的值！

这就好比那个被困在轨道谷底中的小球，在没有获得任何动能的情况下，某一天突然就跳出谷底跑到旁边去了。

这一现象的唯一合理解释就是宏观量子隧穿。

在这个实验中，发生隧穿的并非单个的库珀对，而是代表了整个系统集体行为的"赝粒子"------即那个"小球"所代表的宏观相位。是整个宏观电路的量子态作为一个整体，穿过了能量势垒。

电压的出现，就是这个宏观量子态成功隧穿并进入一个新状态的明确信号。

相位差δ开始随时间快速变化，根据约瑟夫森效应，电压与相位差变化率成正比，即

这就导致了电压的出现，它表明系统整体的稳定被打破。

但这三位物理学家的贡献远不止于此。他们提供了第二个，也是更具决定性的证据，证明了他们观测到的是真正的量子效应------能量量子化。

他们向处于零电压状态的约瑟夫森结施加了微弱的微波辐射。根据量子理论，那个被困在势能谷底（波谷）的"赝粒子"，其能量状态不应是连续变化的，而应该是分立的、一层一层的，就像楼梯的台阶一样。这些不同的能级被称为量子能级。

实验发现，只有当微波的频率精确匹配于理论计算出的两个特定能级之间的能量差时，系统才会有效地吸收能量，从而显著提高其隧穿逃逸的概率。

这就像一把钥匙只能开一把锁，只有能量完全匹配的微波，才能将系统从"基态"激发到"激发态"。

更重要的是，他们观测到了不止一个，而是多个这样的共振频率，与量子力学对离散能级的预测完美吻合。

这项工作首次清晰地展示了，一个宏观尺度下的电路，其能量状态确实是量子化的。

03

宏观量子 vs 微观量子

在这里，很多人会有一个疑问：超导电流本身确实是一种宏观量子效应。那三位诺奖获得者所发现的宏观量子现象，与超导电流所代表的宏观量子效应到底有什么区别呢？

简单地说，它们是不同层级的概念！

超导电流本质上是大量微观个体量子行为的集体表现，是典型的"微观量子隧穿"效应。

而 2025 年诺奖得主所揭示的，是一个宏观尺度的物体作为一个单一的量子实体来行动。

没错，他们发现的是"宏观量子隧穿"现象，类似于"人体穿墙而过"，只是规模上小很多，但却是真正的宏观隧穿现象！

如果要更形象的理解，我们可用下面这样的比喻来说明。

超导电流就像"整齐步伐的队伍"，所有人都以完全相同的节奏和方向齐步前进。这个"齐步走"本身，就是一个令人震撼的宏观有序状态，但它源于每个人（库珀对）的微观行为被约束到了一个统一的模式中。

换句话说，超导电流是一种静态的、稳定的宏观量子有序。它展示了微观量子规则如何导致一个新颖的、稳定的宏观物理性质（零电阻）。

而诺奖实验观测到的，不是这个稳定电流本身，而是描述这个整体军队状态的某个集体变量（即约瑟夫森结两端的相位差），作为一个不可分割的整体，所发生的量子行为。

在没有发生宏观隧穿时，队伍保持稳定的状态，以确定的方向前进------有超流但无电压的量子态。

此时的队伍就像平静的河水，虽然在流动，但整体保持不变。如果比喻成波，它就像没有携带任何状态信息的平面简谐波，换句话说，它是一种宏观上的静态。

在没有任何指挥官用力的情况下，队伍突然"闪现"到另一个状态（比如前进方向或队伍排列模式）------发生了量子隧穿。并且，队伍只能处于几个特定的行进方向或排列模式上------分立能级。

讲到这里，你大概能总结出它们的本质区别了。

超导电流（队伍齐步走） 本身是一个稳定的宏观量子基态，具有宏观量子态的属性。但是它本身并没有穿墙。

而诺奖实验（队伍整体变化） 让我们观测这个宏观量子系统本身的动力学量子行为------它的整体状态如何像一个小小的电子一样，进行概率性的隧穿，并遵循能量量子化的规则。

04

为什么它是诺奖级的？

克拉克、德沃雷和马丁尼斯不仅以精湛的实验技艺回答了物理学的一个基础性问题，更重要的是，他们架起了一座桥梁，将抽象的量子理论世界与我们能够触摸和制造的宏观物理世界连接起来。

他们向我们揭示，量子力学并非一个只存在于教科书中的神秘理论，而是我们未来技术图景中一块坚实而强大的基石。

这项发表于 1980 年代中期的研究成果，其深远意义体现在两个层面。

在基础科学层面，它极大地深化了我们对量子力学适用边界的理解。

它用确凿的实验证据表明，量子力学的奇异特性并不仅限于微观世界。只要环境足够纯净、干扰足够小（例如在超导状态下），由大量粒子组成的宏观系统同样能够展现出纯粹的量子行为。

这为著名的"薛定谔的猫"思想实验提供了一个现实的、可操作的类比，尽管规模要小得多，但原理相通。

在技术应用层面，这项工作是当今量子计算革命的先声。

它证明了超导电路可以被制造成一个人工原子，其量子态可以被精确地控制和测量。

约翰·马丁尼斯后来正是利用这一原理，将约瑟夫森结中最低的两个能级定义为一个量子比特（qubit）的"0"和"1"状态，从而推动了超导量子计算机的迅猛发展。

今天，谷歌、IBM 等公司正在研发的量子处理器，其核心正是基于这一技术路线。此外，基于约瑟夫森结的极其灵敏的测量设备，也早已应用于医学成像和基础科学研究中。

总而言之，2025 年诺贝尔物理学奖所表彰的，是量子力学领域一项真正具有开创性的工作。

参考文献

挑战！通俗理解物理诺奖：量子力学能有多宏观

知乎高赞 2025 年 10 月 08 日 16:48 北京

当地时间 10 月 7 日，2025 年诺贝尔物理学奖授予英国物理学家约翰·克拉克 （John Clarke）、法国物理学家米歇尔·H·德沃雷特（Michel H. Devoret）和美国物理学家约翰·M·马丁尼斯（John M. Martinis），以表彰他们「发现了电路中的宏观量子力学隧穿和能量量子化」。

如何通俗地理解这项成果↓

2025 年诺贝尔物理学奖

颁给电路中宏观量子力学现象

如何通俗地理解这项成果？

答主@拉格朗日的忧郁

浙江大学物理高等研究院凝聚态场论方向

今年诺贝尔物理学奖终于再次回归物理学，特别是在量子力学建立百周年的时间把诺奖再次颁给和量子力学相关的领域，是一个相当让人舒心的结果。

今年的诺奖获得者是 John Clarke,Michel H. Devoret,John M. Martinis，颁奖理由是「for the discovery of macroscopic quantum mechanical tunnelling and energy quantisation in an electric circuit.」翻译过来大致是说：

因发现电路中的宏观量子力学隧穿效应和能量量子化现象。

诺奖委员会应当也是希望往量子力学上靠。

今年诺奖得主中比较为大众所熟知的是 John M. Martinis，这位在量子计算领域是响当当的大人物，谷歌最著名的那篇「量子霸权」的论文便是这位的手笔。但这个工作由于 supremacy 受到了相当的质疑，毕竟他们展示的并不足够充分说明量子优越性。

但今天的故事与此无关，Martinis 在 40 年前就已经取得了让今天的他得享诺奖的工作------超导电子电路的宏观量子现象，他的毕业论文就是这个主题------Macroscopic quantum tunneling and energy-level quantization in the zero voltage state of the current-biased Josephson junction，而他的老板就是今天拿诺奖的另一位大佬------John Clarke。

至于 Michel Devoret，非常奇妙的是，他也在谷歌干，目前是谷歌量子人工智能的首席科学家，看来业界才是量子技术最好的就业方向。

为什么要颁这个诺奖呢？

其实知乎有一个经久不衰的关于诺奖的老问题------量子力学的效应最大能有多大？

而这个诺奖其实就是颁给了这个问题------宏观量子力学效应到底能有多宏观，这个问题足够重要。

我们这么来讲，随着摩尔定律逐步失效，未来的器件发展必定是建立在量子力学基础之上的器件，而宏观量子效应对此来说就非常重要了。在这个意义上，这个诺奖既是发给百年量子力学，又是发给下一代的量子技术。

下面我们来简单介绍一下什么是量子隧穿，而什么又是宏观量子隧穿。

量子隧穿是量子力学最基本的现象。

在经典力学中，假如你想翻过一个坡，那你得跑得最够快，来让你的动能转化为势能，你不能又慢又想能翻坡，这不现实。

但量子力学框架下，这是完全可能实现的，一个粒子完全可能在能量低于一个势垒的情况下有一定的概率穿过这个势垒，这是一个彻彻底底的量子效应，在实验上也很早就被确认了，而且 1986 年的诺贝尔物理学奖------扫描隧道显微镜就是以此为原理设计的。

那么紧接着的问题是，这种量子效应归根结底是一种微观效应，是否有可能让这种效应在宏观也能体现出来呢？

那么 Anthony Leggett 等人就从理论上论证，只要系统与导致退相干的环境耗散耦合足够弱，宏观量子相干性是可能的。但理论设想归理论设想，理论家可以想很多奇奇妙妙的东西，但最终还是要落实到实验上。

随后实验学家找到了一个可能实现的实验平台------约瑟夫森结。简单来说这是两块夹有低势垒的弱耦合超导体系统，库珀对在两侧超导体之间转移使得它们的相位发生一定联系，最终产生的效果就是超导的基本单元 Cooper 对能够以很小的概率从一侧超导体穿越势垒层进入到另一侧超导体，这其实本身就是一种隧穿，而两侧的超导相位差可以视作是一种整体的宏观自由度。

当然这件事情从理论上并不是那么难以理解，发生相干的粒子获得一个整体的波函数，那么再宏观它也得是量子的。他们的思路妙就妙在提高恒定电流偏置来获得一个势阱，而按照标准的量子力学，势阱中的波函数很自然就会出现能量量子化，能级一定是分立的，而在实验上这次获得诺奖的小组发现当微波频率恰好等于两个能级之间的能隙时，粒子会被共振激发到高能级。而隧穿亦是如此，整体的波函数穿过构建的势函数后，宏观的量子隧穿便自动发生。

我们在理论上说起来总是很简单的，但实验学家最终把它实现出来却实在是一件很不容易的事情，他们需要找到合适的平台，需要彻底抑制住噪声，确定一定是发生了宏观量子效应而不是热涨落的结果。而这些极其精细的实验最终也为后来量子技术，特别是在超导量子计算等领域的发展提供了必要条件。

和这份诺奖相关的论文是三位大佬在 1985 年写的 prl（prl>nature,science 的又一力证，开玩笑），这篇文章最后带给了他们诺奖。

顺带一提，这篇文章的引用在 aps 上显示是 313，40 年前的论文，平均一年不到 10 的引用，只能说引用很多时候也反映不了什么。

只可惜 Berry 和 Aharonov 两位老爷子再次陪跑一年，从个人角度来说，这二位的诺奖其实更具有量子力学百周年的纪念意义，不知道老头还能熬多久。

知友讨论

@南野 95：

这几年的物理诺奖不论是气象学家获得还是人工智能、这次谷歌的"宏观量子效应"获得只能说明物理学新的革命性突破长时间没有，只能颁给以前的余音...慢慢变成工程学奖了

@不希望咫尺天涯：

Aharonov 有资格得诺奖，Berry 爵士的 Berry 相位不是他首先提出，他得诺奖估计有争议

@一根弦：

哈哈。你是我见过对 AB 效应最有执念的答主

作者：

毕竟和量子力学基础相关的大佬真没几个了。

via :

热门推荐
01BongoCat - 跨平台键盘猫动画工具02两千字总结：Codex 国内如何安装和使用的教程，以及如何设置中文回答03智能库存管理的需求预测模型：从业务痛点到落地代码的完整实践04GitHub 镜像站点052025羊城杯网络安全大赛 wp06UV安装并设置国内源07Linux下V2Ray安装配置指南08Spring Boot 实现微信登录，So Easy !09Cursor Plan Mode：AI 终于知道先想后做了105大DOM/BOM核心考点：从入门到精通，让面试官眼前一亮