此分类用于记录吴恩达深度学习课程的学习笔记。
课程相关信息链接如下:
- 原课程视频链接:[双语字幕]吴恩达深度学习deeplearning.ai
- github课程资料,含课件与笔记:吴恩达深度学习教学资料
- 课程配套练习(中英)与答案:吴恩达深度学习课后习题与答案
本篇为第一课第二周,是2.7,2.8,2.14,2.15部分的笔记内容,同时,这也是本周理论内容的最后一部分。
本周的课程以逻辑回归为例详细介绍了神经网络的运行,传播等过程,其中涉及大量机器学习的基础知识和部分数学原理,如没有一定的相关基础,理解会较为困难。
因为,笔记并不直接复述视频原理,而是从基础开始,尽可能地创造一个较为丝滑的理解过程。
首先,经过第五部分内容的学习,我们了解了什么是向量化和逻辑回归正向传播的向量化,本篇则继续讲解反向传播的向量化过程和广播机制。
1.链式法则
1.1 什么是链式法则?
链式法则是专门用于复合函数求导的法则,我们直接上一个例子来理解一下这个法则:
我们都知道,相比别的食物,吃甜品会让体重增加的更快 。
我们来细究一下这个关系:
- 吃甜品的数量 \(x\) 影响我们的血糖 \(u\) ,用函数来表示就是:
\[u = g(x) \]
- 血糖 \(u\) 影响我们的体重 \(y\) ,同样用函数表示就是:
\[y=f(u) \]
- 而往往我们会略过血糖这一层,探究吃甜品数量 \(x\) 和体重 \(y\) 之间的关系,即:
\[y =f(g(x)) \]
我们得到的这样形式的函数就是复合函数,它虽然只有一个变量,但是在逻辑上却不只有一次传递过程。
我们在第三部分 里提到过,复合函数的求导其实也就是基本函数导数的运算,而运算的规则,就是链式法则。
1.2 链式法则的实现过程
继续使用刚刚的例子,现在,我们想体重关于吃甜品数量的变化率,即 \(y\) 对 \(x\) 求导,现在来看看具体的传导过程。
- 现在我们按求导定义,让 \(x\) 增加 \(Δx\) ,而在逻辑上,变化是这样传递的:
\[甜品Δx->血糖Δu->体重Δy \]
- 再细化一下:$$血糖Δu=g′(x)Δx$$$$体重Δy=f′(u)Δu$$
- 结合两个公式,我们就得到:$$Δy=f′(u)g′(x)Δx$$
- 最后一步,我们在两边同时除以\(Δx\) ,就会得到:$$y′=f′(u)⋅g′(x)$$
也就是说,体重随甜点变化 = 体重随血糖变化 × 血糖随甜点变化。
变化从前一个"传"到后一个,"传递系数"就是导数,链式法则就是把这些"变化传导率"乘起来。
2.逻辑回归反向传播的向量化
2.1计算总损失
我们回忆一下之前讲解反向传播的过程和对梯度的学习部分,结合上一篇的正向传播过程现在,我们有:
- 损失函数 \(L\)
- 所有样本的加权和向量 \(Z\)
- 所有样本经过激活函数的输出 \(A\)
- 所有真实标签 \(Y\)
根据二分类交叉熵损失函数的定义,我们知道:$$L=−[YlnA+(1−Y)ln(1−A)]$$
通过向量化,我们便通过一次计算得到了 \(m\) 个样本的总损失,这也是在实际上不太常使用代价函数/成本函数的原因之一,因为通过向量化,我们使用损失函数一次便可以得到总损失。
2.2 计算梯度
继续观察,会发现上面的 \(L\) 实际上就是关于 \(Z\) 的复合函数,而实际上,我们要知道权重和偏置对损失的影响,则还需要再过一层,具体如下:
\[权重ΔW和偏置Δb->加权和ΔZ->输出ΔA->损失ΔL \]
现在,我们想要计算梯度,最直接的一层就是:
\[\frac{d L}{d A} = \frac{A-Y}{A(1-A)} \]
这个求导的结果是这样的。
而根据上面的传导过程,我们再往下一层到加权和 \(Z\) :
\[\frac{dL}{dZ} = \frac{dL}{dA} \cdot \frac{dA}{dZ} \]
而对sigmoid激活函数求导的结果是这样:
\[\frac{dA}{dZ} = A(1-A) \]
最终,我们得到:$$\frac{dL}{dZ}=(A-Y)/(A(1-A)) \cdot A(1-A) = A-Y $$
也就是说,我们的经过层层复杂计算后,得到的损失 \(L\) 关于加权和 \(Z\) 的变化率,就是最直观的输出和标签的差异,而这不是在最初为了简化计算规定的,反而是经过层层链式计算得到的。
现在我们再继续向下到最后一层,来计算权重 \(ΔW\) 和偏置 \(Δb\) 对损失的影响。
先回忆一下逻辑回归线性组合得到的加权和公式如下:
\[\mathbf{Z} = \mathbf{W}^T \mathbf{X} + \mathbf{b} \]
我们要求的,即是:
\[每个权重 W_{i} 对损失的影响 → dW=\frac{\partial L}{\partial W}=\frac{dL}{dZ} \cdot \frac{\partial Z}{\partial W},其中\frac{\partial Z}{\partial W}=X \]
\[偏置 b 对损失的影响 → db=\frac{\partial L}{\partial b}=\frac{dL}{dZ} \cdot \frac{\partial Z}{\partial b},其中\frac{\partial Z}{\partial b}=1 \]
在此基础上,再考虑到 \(m\) 个样本求平均损失,即可得到最终的梯度:
\[dW = \frac{1}{m} X^T dZ,其中dZ=A-Y,转置是为了和维度匹配 \]
\[db = \frac{1}{m} \sum_{i=1}^{m} dZ^{(i)},其中dZ^{(i)}=A^{(i)}-Y^{(i)} \]
这便是逻辑回归中通过链式法则得到梯度的过程,有了这部分的了解,我们就可以比较通畅的解释反向传播的向量化中的梯度计算过程。
2.3 更新参数
我们通过计算得到了梯度,最后一步就是使用梯度下降更新参数,如下,这就又涉及到第四部分的学习率了,我们最终更新参数如下:
- 权重参数更新:
\[W := W - \eta \, dW \]
- 偏置参数更新:
\[b := b - \eta \, db \]
\(\eta\) 就是学习率,它可以手动设置,也有一些学习率更新算法。
最终我们遍通过完全向量化的形式进行了一次迭代,而在代码中,不会用到一次显式的for循环。
当然,要强调的一点就是,我们依然需要使用for循环来进行多次训练,多次迭代, 这一步是无法省略的。
再次回看一下传播过程图:
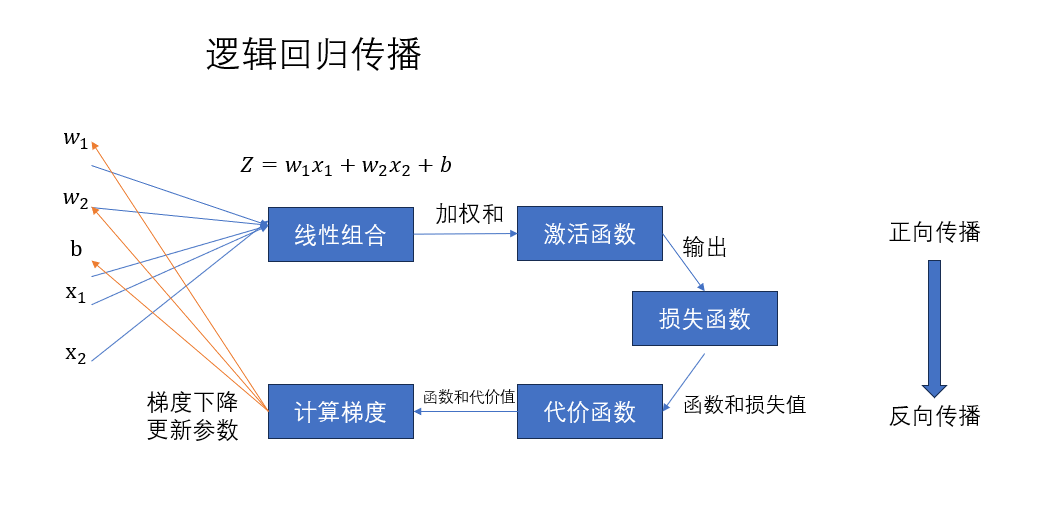
在经过向量化部分的讲解后,对这张图应该也会有更深的理解。
本篇的公式推导较多,其实不理解的话也不必感觉DL的学习过于困难,在实际的代码编程中,我们的模型构建,训练,传播过程都已有相关的库与其内置函数,计算过程也由其自动完成。
个人感觉来说,在这一部分,最低限度的了解应该是知道逻辑回归这样一个简单网络的传播过程,即对上面这张图和其中涉及的概念了解即可。
而下面要讲的广播机制也是实际编程中实现便利的一项。
3.广播机制
吴恩达老师单独用一节课来解释了一下python中的广播机制,因此我们在最后也对这一机制进行简单的介绍。
还是先摆概念:
NumPy 广播机制(Broadcasting)是一个非常强大的功能,它使得不同形状的数组能够进行数学运算时自动对齐。通过广播,NumPy 可以执行不同形状的数组之间的操作,而无需显式地调整它们的维度。广播可以让你写出更简洁和高效的代码。
现在直接上例子,我们来看这样一段代码:
python
import numpy as np #导入numpy库
#定义两个维度不同的数组
A = np.array([[1, 2, 3], [4, 5, 6]]) # 形状 (2, 3)
B = np.array([1, 0, -1]) # 形状 (1,3)
print(f'A:{A}')
print(f'B:{B}')
print(f'A+B:{A+B}')如果笔算, 我们会发现,A+B是不能运算的,因为二者的维度不匹配。
但实际上,这段代码的运行结果如下:

这便是广播机制的应用,通过结果我们会发现,numpy自动将B向下复制了一行来实现维度的匹配。
现在我们便可以解释之前关于偏置 \(b\) 的定义问题,我们继续看下面这段代码:
python
import numpy as np #导入numpy库
#定义向量化的线性组合
X = np.array([[1, 2, 3], [4, 5, 6]]) # 输入,两个样本,三个特征
W = np.array([1,1,1]) #三个特征的权重
b = 5 #偏置
# 将 W 转置并与 X 相乘
W_t = W.reshape(-1, 1) # 转置 W,使其变为 (3, 1) 形状
# 使用广播机制进行矩阵乘法
result = X @ W_t + b # @为矩阵乘法,(2, 3) 与 (3, 1) 相乘,结果是 (2, 1)
print("结果:", result)其运行结果为:

这里我们也可以通过结果发现,numpy自动将偏置 \(b\) 由标量转化为了向量并自动匹配维度。
因此,得益于广播机制,在逻辑回归的实际编码里,我们在向量化其他变量的过程中,只需把 \(b\) 定为标量即可。
经此六篇,我们终于完成了第二周的理论内容,除文中提及到的外,还有一些关于软件使用和代码规范的内容,其中代码规范会在下篇,本周的课后作业:代码实现逻辑回归,中进行提及,而软件使用大家可以自行了解,便不在笔记中出现了。