边缘检测方面传统的算法中最为经典的就是Canny算法,但是标准的Canny是不具有亚像素精度的,而且得到的结果是一堆离散的边缘点,提取亚像素的方式有很多种,这个在网络上还有一些资料,而如何将离散点链接成一根一根的线条,我一直没有什么思路,最近偶然又有朋友给我推荐了一片文章:A Sub-Pixel Edge Detector an Implementation of the Canny /Devernay Algorithm及其配套的代码,终于完了我这个梦,相关论文及代码可以从http://www.ipol.im/pub/art/2017/216/下载和查看。
后面仔细看了看这个配套的代码,应该说其实在四五年前我就下载过,只是当时感觉好复杂,就没有信心一直看下去,没想到原来那个就是答案,所以有的时候坚持还真的很重要。
这篇文章提出了自己的一个亚像素边缘检测思路,同时也提供了把这些边缘点链接为线条的方法,其边缘检测的算法呢我认为一般般,应该说还是没有Canny好吧。这里稍微做点介绍。
** 一、Canny /Devernay边缘检测**
1、计算图像的梯度值(X方向梯度、Y方向梯度以及梯度幅值),这个可以用一阶中心差分,或者二阶中心差分。
这个过程伪代码如下所示(这里使用的是一阶差分):

一般情况下在进行差分前需要进行下小尺度的高斯模糊,以便减少噪音的干扰。
注意,在计算X及Y方向梯度时,需要注意统一一下计算的方向,及要遵循从左到右以及从上到下这样一致性。
2、根据梯度值的特性来初步确定边缘的候选点,并计算其亚像素位置。
具体来说,当我们完成了第一步的梯度计算后,对于每一个点,当其梯度幅值比左右两侧的点都大时,我们认为其是水平边缘点,当其梯度幅值比上下不部位都大时,我们认为其是垂直边缘点,当然也可能出现一个点,其梯度幅值比上下左右都大,这个时候我们还是认为其是水平边缘点。如果不满足这两个条件中的任何一个,则不是边缘点。
通过上面的原则选择了边缘点后,因为这个位置肯定是水平或者垂直方向的最大值,所以呢我们通过领域三个点的二次方插值,可以得到一个局部的最大值,如下面这个曲线所示:
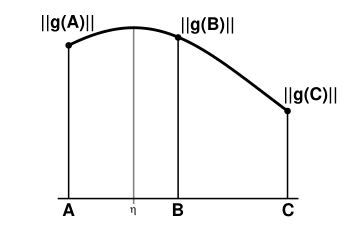
η的坐标即是获取的新的亚像素的边缘点坐标,而且从理论分析可知其和B点的偏差不会大于0.5位置。
η的坐标可用下面的公式计算:
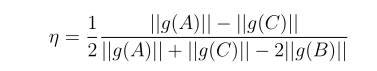
相关的伪代码如下图所示:

注意这里有一个问题,即所获取的亚像素精度只有一个方向的,也就是说如果X方向是亚像素的,那么Y方向就是非亚像素,如果Y方向是亚像素的,那么X方向就是非亚像素。这个是不完美的。
如果不考虑后续的链接成线条的过程,那么下一步就可以直接使用类似于Canny中的双阀值滞后边界跟踪算法了。 但是论文里是先介绍了链接成线的过程。因此我们后面再同步说下这个事情。
二**、离散点链接成线条**
** 1、边缘点链接**
要把离散点链接为线条,首先要把所有点按照一定的规则链接起来,这个链接的规则比较重要。
在没有任何附件条件下,一堆离散点要连接起来,一般来说就是要和最邻近的点相连,这个可以用欧式距离来评判。但是这种原始方案对于边缘检测后的特征来说过于简单了,因为边缘本身还有一定的特性,通常情况下我们不但要考虑两个点的距离,还要考虑两个点的梯度方向等因素,因此,我们制定了以下原则:
(1)、首先两个点要必须都是有效的边缘点。
(2)、第二两个点的梯度方向必须一致,所谓的一致其实是指两个点的梯度方向必须在位于连接两个点的直线的同一侧。
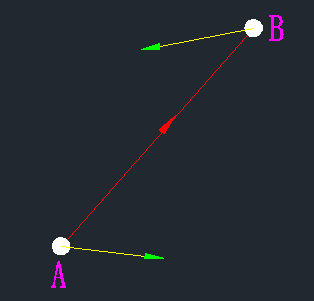
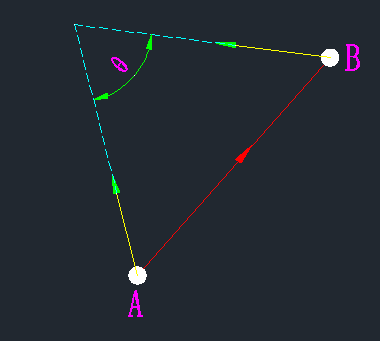
如上左图所示,A和B是两个边缘点,由于A和B两个的梯度方向分别位于直线AB的左侧和右侧,即他们不同边,所以这两个点不能相链接,得分为0,因为他们不同边说明图像在这两个位置的变化趋势不同,他们就属于不同性质的点,所以不连接起来。
而右图,A和B梯度指向同一边,因此我们认为他们性质相同,可以链接。
这是在论文配套的代码里的说法,而论文里则是说A和B处梯度的方向夹角要小于90度,这个似乎也不怎么影响。
对于由两点A(x1,y1)和B(x2,y2)定义的直线,要判断点C(x,y)的位置,则步骤如下:
计算叉积: S = (x2 - x1)*(y - y1) - (y2 - y1)(x - x1)
然后根据符号判断位置:
若S > 0,则点在直线的左侧(相对于从A到B的方向)
若S < 0,则点在直线的右侧.
若S = 0,则点在直线上。
所以如果要求两个点必须在直线的同一侧,那么要么都在左侧,要么都在右侧,所以即要求两个点的S要么同时为正,要么同时为负即两者相乘为正则可。
另外,我们可以规定如果点在直线的左边,表示像素点的梯度方向为前链式传播(forward chaining),即边缘延伸方向与图像扫描方向一致;如果在右边,则表示向后链式传播(backward chaining),即边缘延伸方向与扫描方向相反,这个规定不是强制性的,也可以反过来。
为什么要有这个规定呢,因为一根线条,如果从一端到另外一端,相邻的各点之间梯度方向都是要位于他们之间连线的同一侧的,这样线条才能很明确的作为两个不同性质区域之间的分界线,而不是某两个点符合这个要求。对于每一个点,我们不确定其在线条中是处于前链式中还是后链式中。对于每个点,我们都要计算其最佳的前链式点以及后链式点。注意,当B是A的前链式点时,对应的A就是B的反链式点。
每个点周边可能存在多个符合条件的可链接点,而某一个点最多只能有一个前链点和一个后链点,因此,必须设计出合适的得分评价体系。当两个点确定可链接后,如果判断属于前链式点,则用距离的倒数表示前链式的得分值,即距离越大,得分越低,而属于反向链式,我们则用距离的倒数取反来计量得分,此时,则得分数值越小,越属于最佳反向链接点。为什么要设计这样的方式呢,很明显是为了区分前链和后链。
在具体的实践中,我们一般取计算点周边一定领域的像素来寻找前链和后链,通常3*3就可以了,但是考虑到噪音的影响,把范围扩大到5*5领域更为合理。当我们在搜索范围内找到一个符合初步提条件的前链点B时,需要判断A点是不是在之前的搜索过程中已经有了一个前链点或者B点也已经有了一个后链点,如果有其中之一的情况发生,我们都需要确认新搜索到的距离是否比之前的更短,如果更短,则原先的链接被切断,而新的链接被加入。同样,如果是B是后链点,也存在类似的情况。
这种处理方式也存在一定的瑕疵,即搜索顺序对结果有一定的影响,即结果并不是唯一的,而目前似乎也没有什么特别理想的解决方案,现有的处理流程对大部分结果也是可以接受的。 具体可以看下论文的有关描述。
该部分的相关伪代码如下所示:

贴一部分我整理后的代码:

** 2、根据链接的信息提取每根完整的线条**
当获得了每个点的前后链接信息后,我们就可以从中提取出每个独立的线条信息了。这里的大概流程如下:
按先行后列的方式依次扫描图像中的每一个点,当遇到一个边缘点时做如下处理:
沿着这个边缘的后链式方向寻找,找到最后一个后链式点,这个过程在原始的代码中非常的巧妙,用了一句表面上看上去不含任何循环体的for语句:
for (I = Index; (J = Prev[I]) >= 0 && J != Index; I = J);Index表示当前点的位置,从这个位置开始,如果Prev[I]大于等于0,则说明I这个位置有后链点,并且这个点不是当前点(因为可能有闭合曲线),则把I赋值为Prev[I]进入到下一个点,直到没有后链点了。
当找到第一个后链点,则获得了曲线的起点,然后在按照前链点的坐标依次向曲线的重点寻转,直到找到最后一个前链点。
每找到一根曲线,相应的数据中就增加一些信息,这样就能获取到边缘中的所有曲线了。
** 三、双阀值滞后边界跟踪**
前面提到论文里的边缘后续还要进行双阀值滞后边界跟踪算法,特别是滞后边界跟踪,在传统的Canny里是通过8领域区域生长之类的算法完成的,而如果前期已经进行了边缘点链接,则这个过程就变得非常自然了。
这个过程如下所述:
我们定义一个图像大小的标记变量,先都设置为0,然后按先行后列的方式依次扫描图像中的每一个点,当遇到一个边缘点时做如下处理:
如果这个边缘点的梯度大于高阈值且对应的标记为0,则把标记修改为1,同时,从这个点的位置开始,首先沿着前链点方向依次搜索,如果搜素到的前链点处的梯度幅值小于底阈值,则停止循环,同时把此时的搜索位置的前链点和后链点复位。如果梯度幅值大于低阈值,则标记把对应位置的标记设置为1,这样下次遇到这个点就不用处理了。然后在按照后链点的方向依次搜索,和前链点做同样的处理。
这样做在一个流程里把双阀值及滞后边界跟踪算法同时完成,这是因为通过前面的链接点编码,已经保证了相互链接之间的点的领域相连性,而无需使用区域生长之类的算法了,相当于是水到渠成的事情了。
注意,在处理完成最后,还要有个额外的全图搜索处理过程,即把那些是边缘点且标记依旧为0的点的链接信息复位,这是因为前面的处理对于那些梯度幅值小于低阈值的部分可能没有完全处理到的。
这部分的伪代码如下图所示:

四、相关讨论
论文的配套的代码其实是比较慢的,因为把点链接起来是个较为耗时的过程,这里提出一个方案:
我们可以提前进行阈值的处理,特别是在进行链接点之前我们就进行低阈值的判断,这样就可以筛选掉不少点,有利于后续速度提高。
但是实测呢,这样得到的结果和原始流程的结果不太一致,我想这个应该是和前面讲的链接的不唯一性有一定的关系。但是影响不是很大。
为了对曲线的结果可视化,我们用不同颜色显示不同的线条,这里贴出两个结果图供参考:
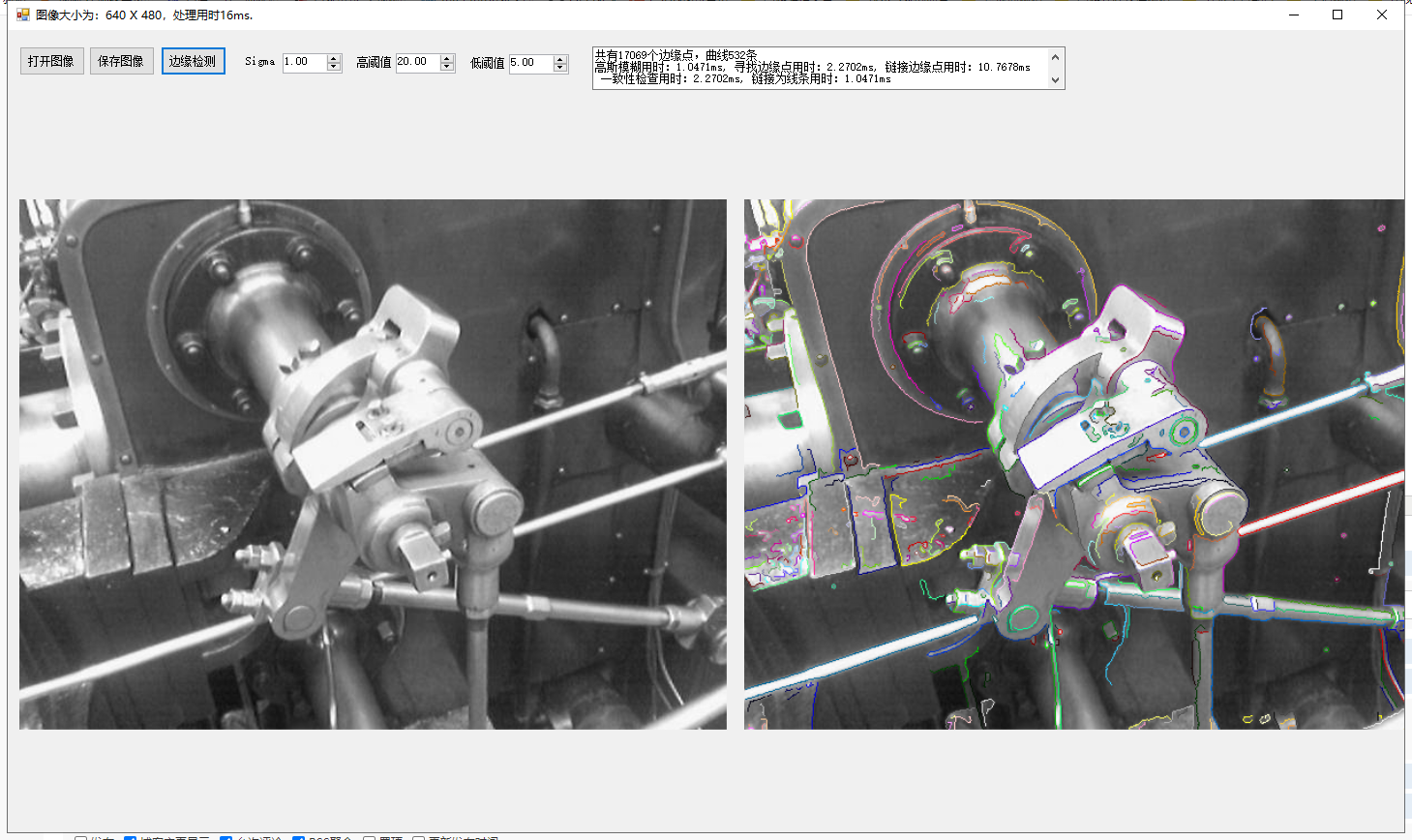
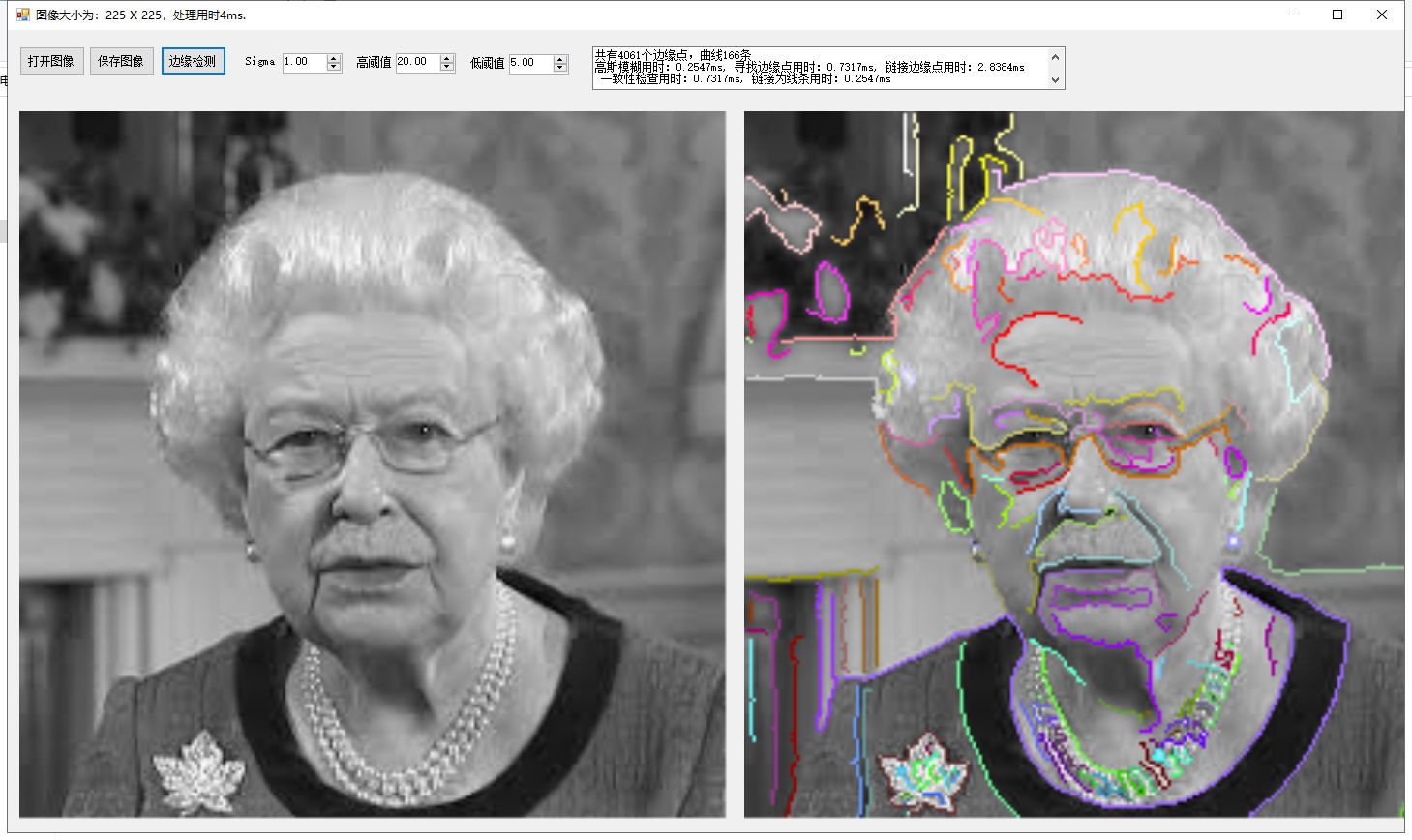
我们把第二个图的局部结果放大查看:
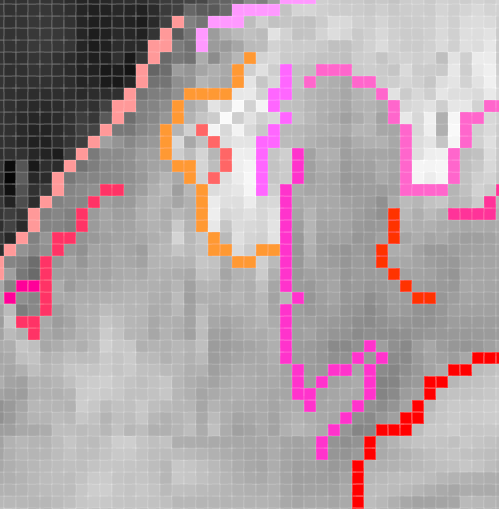
这里有几个相交的线条,算法完美的把他们分开为不同的线条。
这里想到了一些简单的应用,比如把一些小的毛刺给去除掉,即线段长度小于某个数值则删除这个边缘等等。
** 五、基于Canny的亚像素边缘检测和线条提取**
当我们通过标准的Canny边缘检测获取了整数的边缘坐标后,也是可以进一步扩展为亚像素坐标的,在steger的an Unbiased Detector of Curvilinear Structures一文中,通过Facet Model method模型引入了相关汉森矩阵的特征值等信息,结合3*3领域相关的梯度幅值数据,有效的获取了X和Y方向的亚像素坐标数据,注意这里不是单独X或Y方向亚像素了。这样在结合前面的线条提取等技术,就可以完成Canny算法的后续扩展,而且Canny本身速度是非常快的,且已经进行了双阀值滞后边界跟踪,因此,提取出的边界点相对来说是比较少的了,后续的曲线链接和提取的计算量下降的比较厉害,因此,扩展的耗时也是可控的。
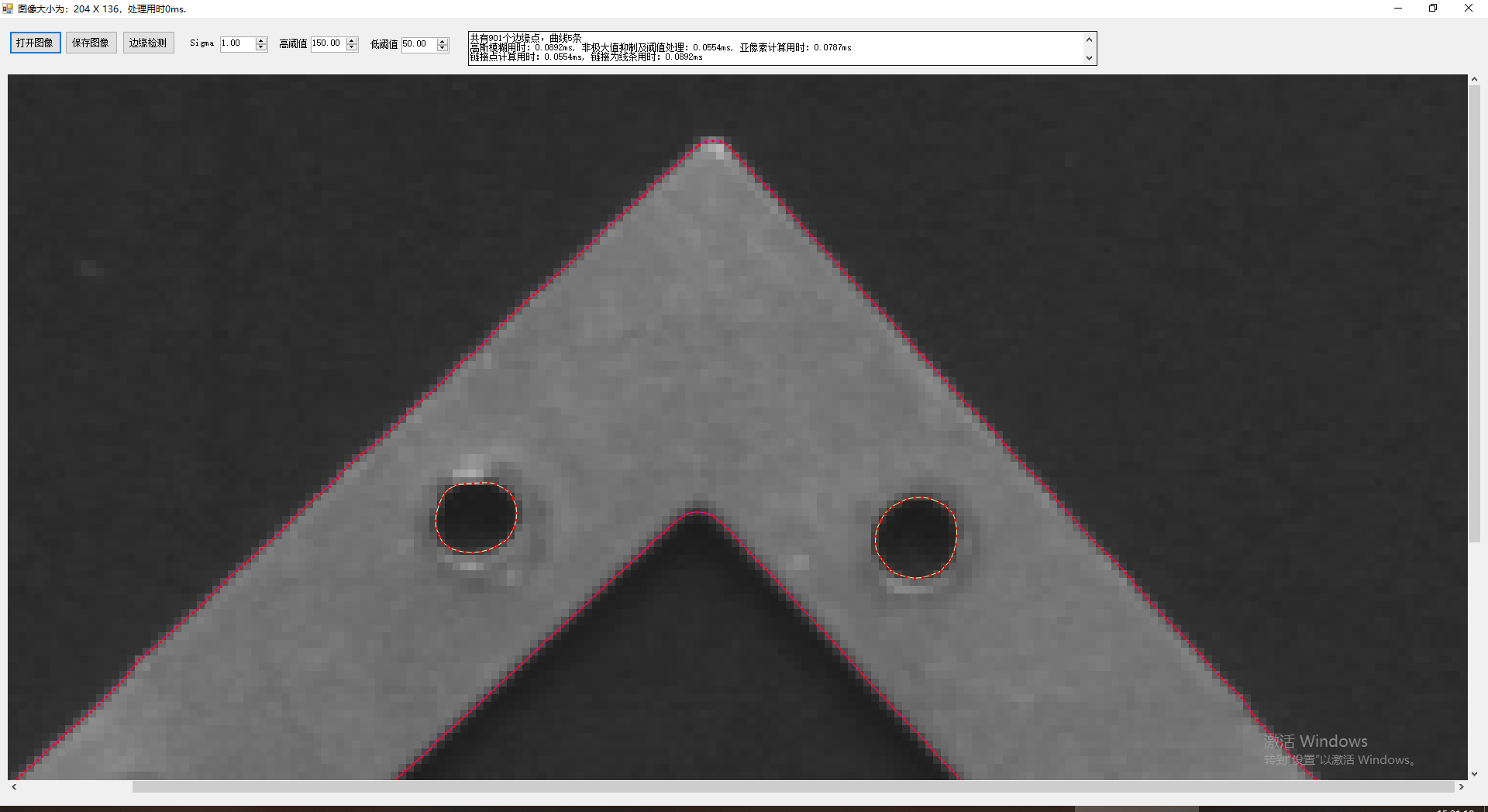
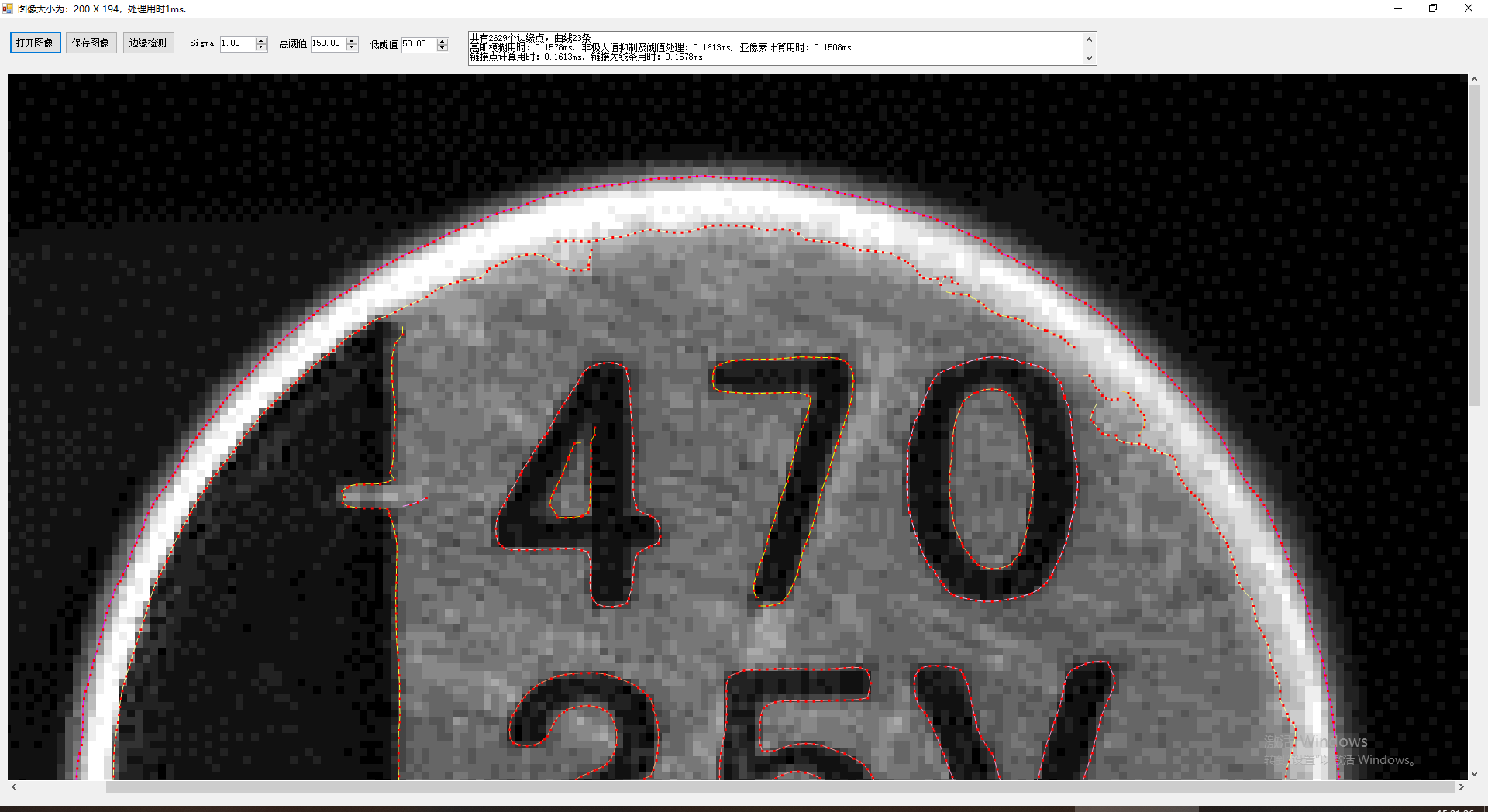
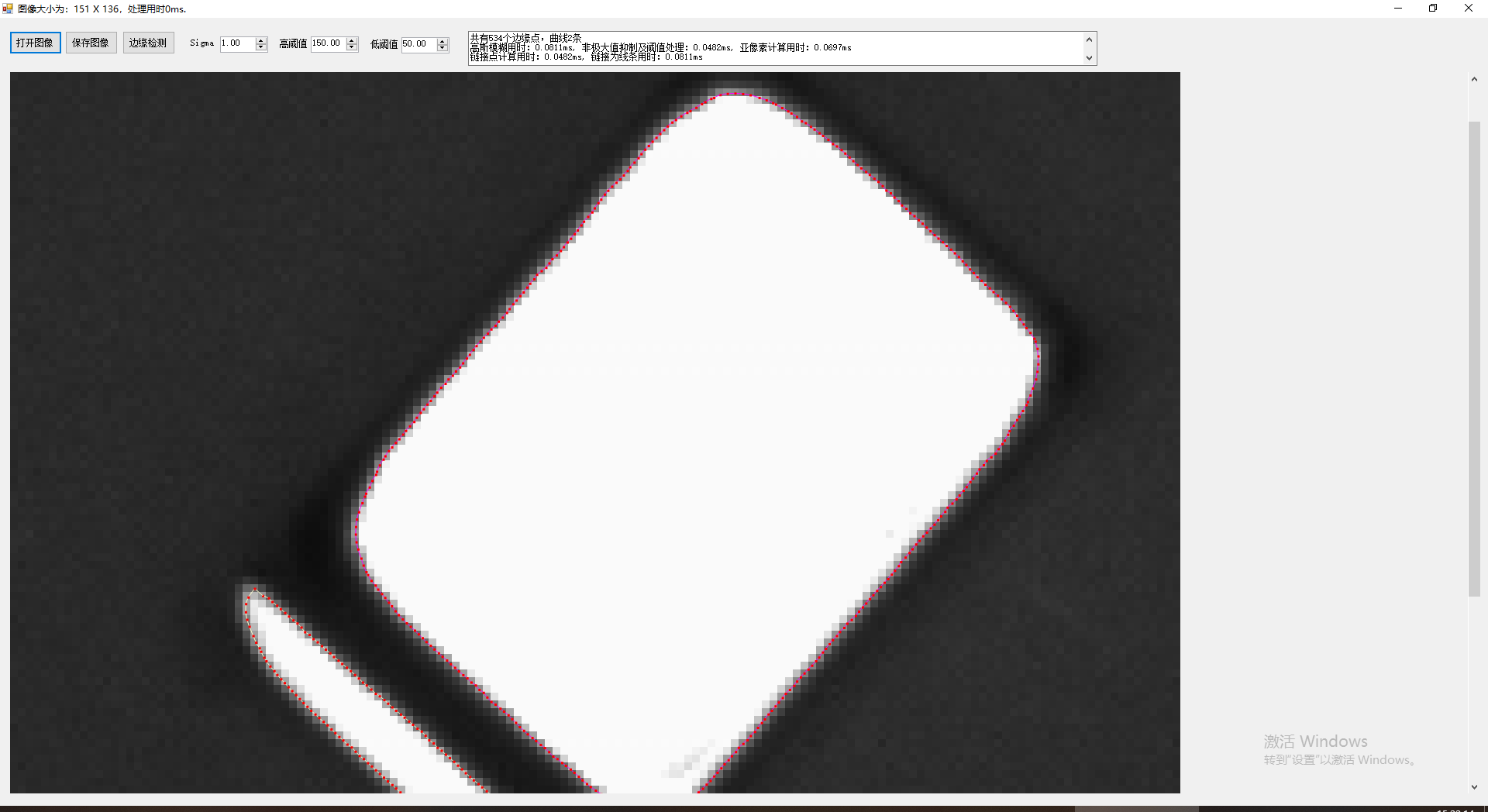
从以上几图,可以明显的看到无论在精度还是展示效果上,扩展的Canny都有着不错的结果,而目前几乎所有的成熟的商业软件中,显示边界时都是提取程曲线显示,而不是简单的显示为点,这不仅仅看上去更为高端,实际也能获取更多的手段对检测的结果进行进一步的提取和挖掘。
实际上,在编写这方面的程序时还有很多的细节,比如很多亚像素提取的代码都把边界偏移限制在0.5,即如果识别到的亚像素大于0.5,则不做亚像素处理,实际上,这个值可能要放大到0.6甚至0.8,这样才能保证处理后的边界连接起来才足够平滑。这一点在steger的有关论文里也有提及。
我这里提供两个DEMO供大家测试,一个是直接显示Canny亚像素及曲线提取的结果,一个是放大显示结果,注意:由于我没有做动态的放大图像流程,因此这个DEMO的输入图像不要大于500*500。
https://files.cnblogs.com/files/Imageshop/Canny.rar?t=1760599971&download=true
https://files.cnblogs.com/files/Imageshop/CannyZoom10.rar?t=1760599962&download=true