P14322 「ALFR Round 11」E 空崎ヒナ 题解
Sorasaki Hina 赛高!
也是做上 BA 的题了!也是写上 BA 的题的题解了!我们 BA 厨的日子真是蒸蒸日上啊!
求审核大大通过 QvQ。求求了!
题目描述:给出若干次询问,每次询问给出 \([l,r]\),求 \(\sum_{i = l}^{r} [b_i \equiv x\pmod {\displaystyle\max_{l\le j\le i}a_j}]\)。
这种一句话题意总感觉在做 ynoi?
很容易我们可以将题意转化为求 \(\sum_{i = l}^{r} [\lvert b_i - x \rvert \mid {\displaystyle\max_{l\le j\le i}a_j}]\)。
然后怎么做呢?
首先转化完题意后发现 \(b\) 数组没有直接用到,可以在输入的时候直接减去 \(x\)。下文中提到的 \(b\) 数组都是减完 \(x\) 后的 \(b\) 数组。
因为发现左端点的位置对后边的贡献有影响,所以是不好直接去维护的。
所以最开始我想的是用回滚莫队,将问题离线后按左端点为第一关键字,右端点为第二关键字排序,然后枚举左端点所在块,右端点直接跑即可。
但是这样的话就有一个问题。
那就是从左端点到块的右端点中的值会对块的右端点后边的值产生影响。
这可能有点拗口,举个例子解释一下。
比如说有一个询问是从 1 到 5。
\(b\) 数组为 1 4 2 3 4。
假设 1 所在块的右端点为 2。那么我们可以直接求出 \([1,2]\) 和 \([3,5]\) 的贡献,而在这其中,参与到答案的 \(max_{a_i}\) 则为
1 4 2 3 4。
可这显然是不对的,因为正确的 \(max_{a_i}\) 应该是
1 4 4 4 4。
才对。
我们发现,错误的贡献在于从 3 到 4 这一个区间。
也就是从右端点指针的开头 到最大值小于左端点指针暴力遍历的最大值的这个区间。
如果还是不理解的话,可以画个图来理解一下。
如下图所示,其中黑色的竖线是右端点遍历的起点,竖线右边的红线是右端点指针遍历中求的最大值。
竖线左边的黑线是左端点指针暴力遍历的最大值。
竖线右边的红线是对答案贡献有误的区间(因为该区间内的 \(mas{a_i}\) 在统计时是错误的)。
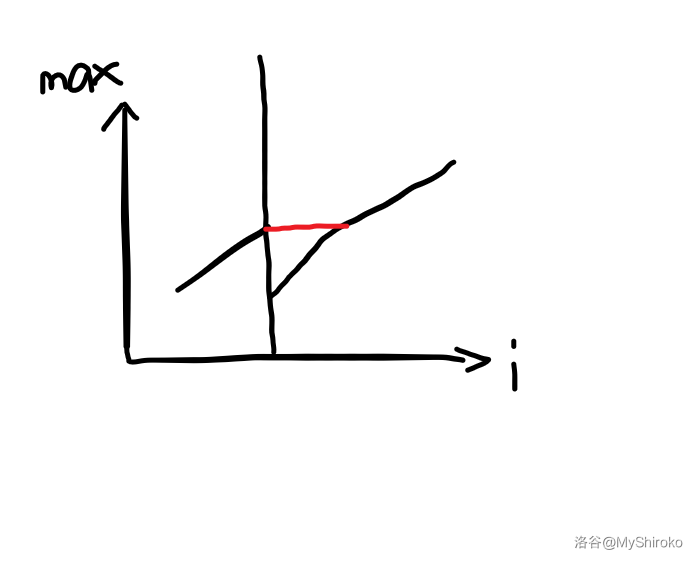
然后我们考虑怎么去除这部分错误贡献。
首先,考虑到这种贡献有且仅有当左端点左移时产生,但是如果左端点右移,我们将无法处理新的贡献。
所以扩展刚才我们的思想,直接上扫描线(其实是因为回滚莫队时间复杂度不正确)。
考虑直接将左端点从大到小排序。每次将左端点加上即可。
然后每次二分地查出其错误贡献的区间,然后修正这部分去权值即可。
对于像上图竖线之后的贡献,我们可以直接从左到右遍历一遍即可。
但是这样又有一个问题,如果我们询问的右端点在错误的区间之中,那么我们将无法处理。
这时候,曾经被 ynoi 折磨的经历呈现在眼前,欸,好像可以吧这部分贡献二次离线下来,统一做差分处理。
现在,我们的问题转化成了如何去简单地求一段区间 \([l,r]\) 内,给定 \(val\) 求 \(\sum_{i = l}^{r} [\lvert b_i - x \rvert \mid val]\)。
很容易我们想到对于每个 \(b\) 去预处理出其所有的因子,每次只需要检查因子是否含有 \(val\) 即可。
但是我们发现处理因子是 \(O(n \sqrt(n))\) 的,光预处理就会 TLE!
怎么办?
感谢机房巨佬 luochaoqiang的解答。
我们发现,处理每个数会 TLE,但是如果处理值域内的所有数的因数,这样做是 \(O(n log{n})\) 级别的。
这样我们的时间复杂度就正确了!
但是常数极大
需要略微卡常即可通过此题。
代码有注释,请放心食用。
cpp
#include <bits/stdc++.h>
#define Blue_Archive return 0
#define con putchar_unlocked(' ')
#define ent putchar_unlocked('\n')
using namespace std;
constexpr int N = 1e6 + 3;
constexpr int V = 1e6;
int n;
int m;
int x;
int cnt;
int top;
int a[N];
int b[N];
int r[N];
int ans[N];
int num[N];
int zor[N];
int stk[N];
int sum[N];
int val[N];
int siz[N];
int tmp[N];
struct hina
{
int l,r,id,op;
}q[N],L[N << 1];
vector<int> vec[N];
inline int read()
{
int k = 0,f = 1;
int c = getchar_unlocked();
while(c < '0' || c > '9') c = getchar_unlocked();
while(c >= '0' && c <= '9') k = (k << 3) + (k << 1) + (c ^ 48),c = getchar_unlocked();
return k * f;
}
inline void write(int x)
{
if(x < 0) putchar_unlocked('-'),x = -x;
if(x > 9) write(x / 10);
putchar_unlocked(x % 10 + '0');
}
inline int find(int val)
{
int l = 1,r = top,mid = 0,res = 0;
while(l <= r)
{
mid = (l + r) >> 1;
if(stk[mid] <= val) r = mid - 1,res = mid;
else l = mid + 1;
}
return stk[res];
}
signed main()
{
// freopen("data.in","r",stdin);freopen("data.out","w",stdout);
n = read();
m = read();
x = read();
for(int i = 1;i <= V;i ++) // 先算好 vector 的空间,再申请内存可以减小常数(详见 P12525 [Aboi Round 1] 私は雨 )
{
for(int j = 1;j * i <= V;j ++)
{
siz[i * j] ++;
}
}
for(int i = 1;i <= V;i ++) vec[i].reserve(siz[i]); // 申请内存
for(int i = 1;i <= V;i ++) // 预处理
{
for(int j = 1;j * i <= V;j ++)
{
vec[i * j].emplace_back(i);
}
}
for(int i = 1;i <= n;i ++) a[i] = read();
for(int i = 1,tmp;i <= n;i ++)
{
b[i] = read() - x; // 对于 b 数组直接减去 x (通过题意转化可得)
if(b[i] < 0) b[i] = -b[i]; // 要判负!!!
zor[i] = zor[i - 1] + (!b[i]); // 0 的话一定有贡献,做一个前缀和
}
for(int i = 1;i <= m;i ++) q[i].l = read(),q[i].id = i; // 离线处理问题
for(int i = 1;i <= m;i ++) q[i].r = read(),ans[i] = zor[q[i].r] - zor[q[i].l - 1];
sort(q + 1,q + m + 1,[](hina a,hina b){return a.l > b.l;}); // 将左端点从大到小排序
for(int i = 1;i <= n;i ++)
{
while(top && a[stk[top]] < a[i]) r[stk[top --]] = i - 1; // 用单调栈求出每个断点的管辖区间(即该值可能作为最大值的区间)
stk[++ top] = i;
}
while(top) r[stk[top --]] = n;
for(int i = 1;i <= n;i ++) // 差分,上扫描线
{
L[++ cnt] = {i,a[i],i,1};
L[++ cnt] = {r[i] + 1,a[i],i,-1};
}
sort(L + 1,L + cnt + 1,[](hina a,hina b){return a.l > b.l;});
for(int i = 1,l = n;i <= cnt;i ++)
{
while(L[i].l <= l && l)
{
if(b[l]) for(int v : vec[b[l]]) ++ num[v]; // 用一个桶维护因数出现次数
l --;
}
val[L[i].id] += L[i].op * num[L[i].r];
}
top = cnt = 0;
for(int i = 1,l = n,tot = 0,pos;i <= m;i ++)
{
while(q[i].l <= l && l)
{
while(top && stk[top] <= r[l]) tot -= val[stk[top --]]; // 在其掌控区间内的答案
stk[++ top] = l;
tot += val[l]; // 做一个后缀和
sum[l] = tot;
l --;
}
pos = find(q[i].r); // 二分查找出
ans[q[i].id] += tot - sum[pos]; // 查分求答案
L[++ cnt] = {pos,a[pos],q[i].id,1}; // 二次离线求剩余区间的贡献
L[++ cnt] = {q[i].r + 1,a[pos],q[i].id,-1};
}
sort(L + 1,L + cnt + 1,[](hina a,hina b){return a.l > b.l;});
for(int i = 1,l = n;i <= cnt;i ++)
{
while(L[i].l <= l && l) // 再上一次单调栈,从后往前扫
{
if(b[l]) for(int v : vec[b[l]]) tmp[v] ++; // 跟上边一样
l --;
}
ans[L[i].id] += L[i].op * tmp[L[i].r];
}
for(int i = 1;i <= m;i ++) write(ans[i]),con;
Blue_Archive;
}