相平面控制:深入解析一种经典的非线性控制系统设计方法
在现代控制理论中,尽管线性控制系统设计方法(如PID控制)占据了主导地位,但在处理高性能、非线性或快速响应的系统时,一种源自经典控制理论的方法依然闪耀着独特的光芒------这就是相平面控制 。它以其直观的图形化分析和强大的应对非线性能力,在航天、机器人等尖端领域发挥着不可替代的作用。
一、 历史渊源:从数学到工程
相平面法的根源可以追溯到19世纪末的数学物理学,由法国数学家亨利·庞加莱在研究天体力学和微分方程定性理论时首次系统提出。他意识到,对于复杂的非线性微分方程,往往难以求得精确的解析解,但可以通过分析系统在"相空间"(对于二阶系统即相平面)中的轨迹来定性了解系统的全部动态行为。
直到20世纪中叶,随着控制系统工程的蓬勃发展,工程师们开始将这一强大的数学工具应用于解决实际工程问题。特别是在早期继电器控制系统、伺服系统和航天器姿态控制中,相平面法因其能直观地处理非线性 (如死区、饱和、滞环)和开关控制 而备受青睐。它成为了设计和分析Bang-Bang控制(时间最优控制)系统的核心工具。
二、 核心概念与定义
1. 什么是相平面?
对于一个用二阶微分方程描述的系统:
ẍ = f(x, ẋ)
我们可以通过引入状态变量来将其转化为一个二维系统:
- 令
y₁ = x(代表位置) - 令
y₂ = ẋ(代表速度,即位置的一阶导数)
这个由 x(位置)和 ẋ(速度)张成的二维平面,就是相平面。
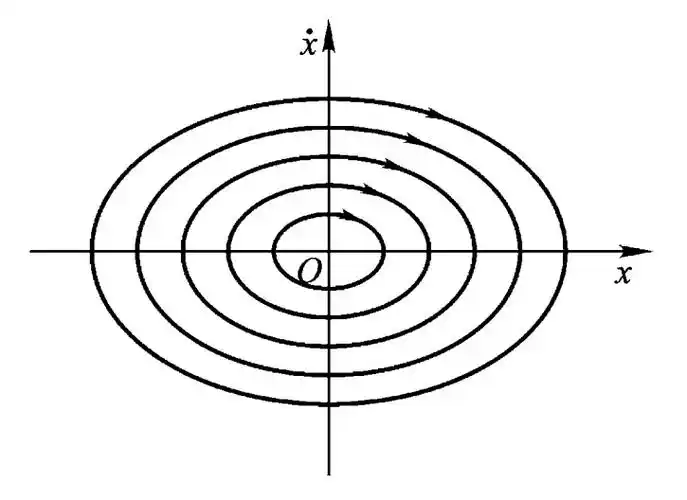
2. 什么是相轨迹?
相平面上的一个点 (x, ẋ) 代表了系统在某一时刻的完整状态 。随着时间推移,这个状态点移动形成的轨迹,就称为相轨迹 。一族相轨迹构成了系统的相 portrait,它清晰地描绘了系统所有可能的运动模式。
3. 平衡点
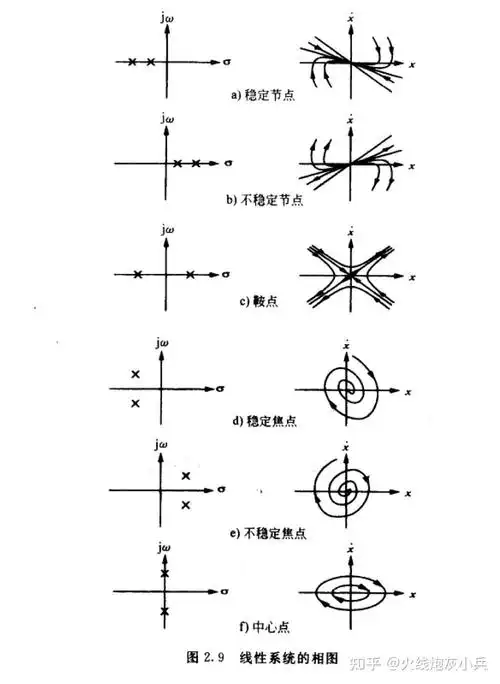
在相平面上,满足 ẋ = 0 且 ẍ = 0(即速度加速度均为零)的点称为平衡点。系统如果处于平衡点,且无外部扰动,将保持静止。相轨迹的形状,特别是围绕平衡点的形状,揭示了系统的稳定性(如稳定焦点、稳定节点、鞍点等)。
三、 基本原理
相平面控制的核心思想是:在相平面上,预先设计好一条或多条"开关曲线"或"切换线",将相平面划分为若干个区域。系统运行时,根据其当前状态点 (x, ẋ) 所在的区域,实时切换不同的控制律(通常是简单的开关控制或线性反馈),从而引导相轨迹最终到达期望的平衡点(通常是原点)。
这种方法本质上是一种分段控制,它将一个复杂的非线性全局控制问题,分解为多个简单的局部控制问题。
四、 方法特点
优点:
- 直观性强:图形化的分析方法使得系统的动态特性一目了然,易于理解和设计。
- 处理非线性能力强:天然适合处理继电器、饱和、死区等非线性特性,而这些是线性PID控制器难以妥善处理的。
- 快速性 :当与Bang-Bang控制结合时,能提供理论上的时间最优控制,使系统以最快速度收敛。
- 物理意义明确 :状态变量
(x, ẋ)通常直接对应物理世界中的位置和速度,控制器的设计非常贴合物理直觉。 - 鲁棒性:对于模型不确定性和扰动,具有良好的鲁棒性,尤其是在开关控制模式下。
缺点:
- "维度灾难" :经典相平面法主要适用于二阶系统。对于高阶系统,相空间维度增加,变得难以可视化和设计。
- 分析复杂:对于复杂系统,手工绘制和分析相轨迹非常繁琐。
- 抖振问题:在开关线附近,微小的噪声或扰动可能导致控制量的高频切换,引起执行机构磨损和系统抖振。
- 精度限制:纯粹的Bang-Bang控制在平衡点附近会产生极限环,无法实现高精度稳定。
五、 基本设计与分析方法
- 系统建模:建立被控对象的二阶微分方程模型。
- 绘制相 Portrait:通过等倾线法、解析法或数值仿真法,绘制出系统在无控制或初始控制下的相轨迹图。
- 设计开关曲线:根据性能指标(如时间最优、能量最优),在相平面上设计一条或多条开关曲线。最常见的是最优开关曲线,它使得系统从任何初始状态出发,都能以最快速度到达原点。
- 定义控制律 :为每个区域分配控制动作。例如:
- 区域 A:
u = +U_max - 区域 B:
u = -U_max - 在开关线上进行切换。
- 区域 A:
- 仿真与验证:通过数值仿真,验证闭环系统的相轨迹是否能平滑、快速地收敛到平衡点。
- 工程优化 :为克服抖振,常引入滞环 或线性区。即在开关线附近设置一个"死区"或平滑过渡区,当状态进入此区域时,采用线性控制或保持原控制,以避免频繁切换。
六、 应用领域
- 航天器姿态控制:是最经典的应用场景,如卫星、飞船的喷气姿态控制。
- 机器人控制:用于机械臂的快速点对点运动、平衡机器人控制。
- 电力电子与电机驱动:逆变器、转换器的控制。
- 伺服系统:高精度、快速定位的平台。
- 车辆防抱死系统:早期ABS系统采用类似相平面的逻辑进行控制。
七、 应用实例:卫星单轴姿态的喷气控制
为了更具体地展示相平面控制的应用,我们考虑一个经典的工程问题:卫星的单轴姿态控制。
1. 问题描述
假设我们控制卫星绕其Z轴旋转(偏航轴)。目标是使用一对反作用喷气推力器,将卫星的姿态角 θ 快速、准确地调整并稳定到 0 度。
- 被控对象:卫星单轴姿态动力学。
- 状态变量 :
θ(横轴):姿态角偏差,即当前角度与目标角度(0度)的差值。ω = dθ/dt(纵轴):角速度。
- 执行机构 :一对反作用推力器,只能提供大小固定、方向相反的力矩。因此,控制输入
u只能是:+U_max(开启一个方向的推力器,产生正力矩)0(关闭所有推力器)-U_max(开启另一个方向的推力器,产生负力矩)
2. 相平面设计与控制律
我们的任务就是在 θ-ω 相平面上设计开关策略,告诉卫星在什么状态下应该执行哪种喷气指令。
a) 最优开关曲线
理论上,时间最优控制(Bang-Bang控制)的开关曲线是一条通过原点的抛物线。为了简化工程实现,我们常用一条通过原点的直线来近似这条最优曲线。
我们定义一条开关线:
S = θ + k * ω = 0
其中 k 是一个精心选择的正数增益。
b) 控制策略与区域划分
这条开关线 S=0 将相平面划分为两个主要控制区域。基于此,我们可以制定一个初步的、理想化的控制律:
- 规则 1 :如果
S > 0(即状态点(θ, ω)位于开关线上方),则施加最大负力矩u = -U_max。 - 规则 2 :如果
S < 0(即状态点(θ, ω)位于开关线下方),则施加最大正力矩u = +U_max。
c) 理想相轨迹示意图
下图描绘了在上述控制律下,系统从不同初始状态出发的相轨迹:
ω (角速度)
↑
| 区域 II (S < 0) 轨迹C
| u = +U_max ↗
| ↗
| ↗
| /
| /|
----------o---------------/--o---------> θ (姿态角偏差)
| / |
| / |
| / |
| / |
| 区域 I (S > 0) |
| u = -U_max |
| 轨迹D
|- 轨迹 A -> B :卫星初始有正的角度和正的速度(状态点A)。它位于区域 I (
S>0),因此施加-U_max进行制动。轨迹向左弯曲,直至穿过开关线S=0到达点B。 - 切换 :在点B,控制立即从
-U_max切换到+U_max。 - 轨迹 B -> O :状态点进入区域 II (
S<0),施加+U_max继续"推着"卫星向原点运动。轨迹再次弯曲,最终以"之"字形路径收敛到原点(0,0)。 - 轨迹 C 和 D:展示了从其他初始状态出发,最终都能被"吸引"到原点。
3. 工程实践中的改进
上述理想控制在实际中会遇到问题:抖振 。在开关线附近,微小的测量噪声就可能导致控制信号在 +U_max 和 -U_max 之间高频切换,使推力器频繁开关,浪费燃料并可能引发结构振动。
为了解决这个问题,工程师们引入了 "滞环" 或 "线性死区"。
改进策略:
我们增加一条平行的开关线,形成一个"滞环带"。
- 上线 :
S_upper = θ + k * ω = δ(δ > 0) - 下线 :
S_lower = θ + k * ω = -δ
新的控制律变为:
- 当状态从上方进入,穿过上线
S_upper时,控制才从-U_max切换为0(或一个较小的力矩),而不是+U_max。 - 在滞环带内部 (
-δ < S < δ),控制保持为0,允许系统靠惯性滑行。 - 只有当状态从下方穿过下线
S_lower时,控制才切换为+U_max。
改进后的示意图描述:
在原有相平面图中,开关线 S=0 被两条虚线 S=δ 和 S=-δ 所夹的带状区域所取代。相轨迹在触及这个带状区域的边界时才会切换控制力,并在带状区域内保持无控制滑行,从而平滑地穿过原点,彻底消除了高频抖振。
实例总结
通过这个实例,我们看到相平面控制如何将一个复杂的动力学控制问题,转化为一个基于简单几何规则的状态决策问题。它充分利用了执行机构的特性,以实现快速响应,同时通过引入"滞环"等工程技巧,巧妙地克服了其固有的抖振缺陷,最终实现了一个高效、可靠、适用于航天环境的控制系统。这种设计思想至今仍在许多高性能、非线性控制系统中广泛应用。
结论
相平面控制作为一种历史悠久且经受了实践考验的方法,其在处理二阶非线性系统、特别是涉及开关执行机构的系统时,展现出无与伦比的直观性和有效性。尽管在高阶系统中其应用受限,但它的核心思想------基于系统状态空间的分区域决策------已经融入到现代控制理论的诸多分支中,如滑模控制。对于控制工程师而言,掌握相平面法不仅是理解一类重要控制系统的基础,更是培养系统动态直觉的宝贵工具。