理论与数学:电子工程实践的双翼
------从课堂公式到电网检修、5G基站与医疗设备的真实应用
在电子工程的学习中,我们常听到"理论联系实际"这句话。但究竟如何联系?理论模型和数学工具到底用在哪里?答案就藏在每一台示波器的波形里、每一块PCB的走线中、每一次电网故障的定位过程里 。本文将通过多个真实工程场景,展示理论与数学如何成为工程师手中不可或缺的利器。
一、理论模型:构建"理想基准",指导现实设计
1.1 模拟电路:放大器Q点设计避免失真
- 场景:某音频功放产品在大音量时出现削波失真。
- 理论应用:通过直流分析计算晶体管的静态工作点(Q点),确保其位于负载线中点,留出足够动态范围。
- 结果:调整偏置电阻后,Q点回归合理位置,失真消失。若无理论支撑,只能靠反复试换电阻"碰运气"。
1.2 高频电子线路:阻抗匹配提升功率传输效率
- 场景:手机射频前端PA(功率放大器)输出功率不足,导致信号弱、掉网。
- 理论应用:利用史密斯圆图和 H(jω) 分析,设计LC匹配网络,使天线阻抗(通常50Ω)与PA输出阻抗共轭匹配。
- 结果:反射系数 ∣Γ∣ 从0.4降至0.05,发射效率提升30%。
1.3 电力系统:短路电流计算保障保护装置整定
- 场景:变电站发生短路,但断路器未及时跳闸,造成设备烧毁。
- 理论应用:基于戴维南等效和对称分量法,计算最大三相短路电流(如50kA),据此整定继电保护的动作阈值和延时。
- 结果:重新整定后,同类故障下断路器在20ms内可靠动作,避免事故扩大。
二、实测对比:发现偏差,精准定位问题根源
2.1 高速数字电路:眼图闭合源于阻抗不连续
- 场景:服务器主板上PCIe 4.0链路误码率高。
- 实测 vs 理论:仿真预测眼图张开度>80%,但实测眼图严重闭合。
- 原因定位:TDR(时域反射计)测量发现过孔处阻抗突变至65Ω(目标50Ω),引发信号反射。
- 解决:优化过孔反焊盘尺寸,阻抗恢复至50±5Ω,误码率达标。
2.2 射频滤波器:截止频率偏移因PCB寄生参数
- 场景:Wi-Fi 6模块(2.4GHz/5GHz)带外抑制不足,干扰邻道。
- 实测 vs 理论:设计截止频率5.8GHz,实测仅5.2GHz。
- 原因定位:使用矢量网络分析仪(VNA)结合电磁仿真,确认微带线边缘耦合引入额外分布电容约0.3pF。
- 解决:缩短耦合长度并增加接地屏蔽,性能回归设计指标。
2.3 电网检修:零序电流异常指示单相接地故障
- 场景:10kV配电网频繁跳闸,但无明显短路迹象。
- 实测 vs 理论:正常运行时零序电流应≈0,但监测显示持续存在15A零序电流。
- 原因定位 :依据对称分量法,判断为单相接地故障(非金属性,高阻接地)。
- 解决:巡线发现某绝缘子因污秽闪络,更换后零序电流归零,系统恢复正常。
三、数学工具:在真实工程中"解题"的利器
3.1 电路分析:微分方程控制开关电源瞬态响应
-
场景:电动汽车OBC(车载充电机)在插拔枪瞬间输出电压过冲,损坏电池管理系统。
-
数学应用 :建立Buck电路状态方程:
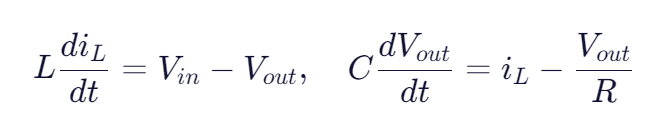
求解特征根,发现系统处于欠阻尼状态。 -
解决:增加输出电容ESR或加入RC缓冲网络,使系统临界阻尼,过冲消除。
3.2 电磁场与电磁波:麦克斯韦方程指导天线设计
- 场景:5G基站毫米波天线阵列增益不达标。
- 数学应用:在HFSS中求解麦克斯韦方程组,发现单元间互耦导致方向图畸变。
- 解决:引入电磁带隙(EBG)结构抑制表面波,隔离度提升12dB,阵列增益达标。
3.3 信号与系统:傅里叶变换用于心电监护仪去噪
-
场景:医院ICU心电监护仪显示波形叠加大量工频干扰(50Hz)。
-
数学应用 :对采集信号做FFT,识别50Hz及其谐波峰值;设计IIR陷波滤波器:
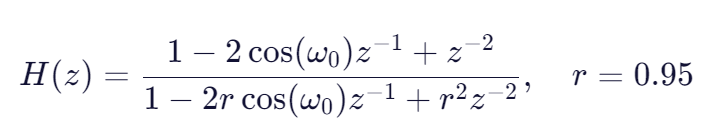
-
结果:干扰抑制40dB以上,QRS波清晰可辨,辅助医生准确诊断心律失常。
3.4 控制系统:状态反馈稳定无人机姿态
- 场景:四旋翼无人机在强风中剧烈晃动甚至坠毁。
- 数学应用:建立六自由度动力学模型,线性化后得状态空间方程;通过极点配置设计状态反馈矩阵 K,将闭环极点置于左半平面。
- 结果:姿态角波动从±15°降至±3°,抗风能力显著提升。
3.5 电力系统:拉普拉斯变换分析暂态过电压
-
场景:特高压输电线路合闸时产生操作过电压,威胁绝缘子安全。
-
数学应用 :将线路等效为分布参数模型,用拉普拉斯变换求解合闸瞬间电压分布:
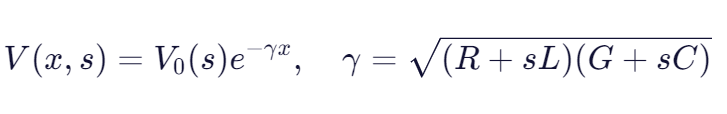
-
结果:预测最大过电压达1.8 p.u.,据此加装合闸电阻或避雷器,有效抑制过压。
四、结语:从实验室到现场,理论与数学从未缺席
无论是:
- 在芯片封装厂调试高速SerDes链路的眼图,
- 在变电站手持钳形表测量零序电流排查接地故障,
- 在5G基站塔下用频谱仪验证天线旁瓣抑制,
- 还是在ICU病房依靠滤波后的心电信号抢救生命,
背后都站着同一个"隐形助手"------由理论构建的认知框架,和由数学提供的计算能力。
工程师的价值,不在于记住多少公式,而在于知道何时用哪个模型、哪种数学工具,去解释一个现象、解决一个问题 。正如一位老工程师所说:"示波器不会告诉你为什么波形失真,但你的理论会。"
持续夯实基础,才能在面对真实世界的复杂与噪声时,依然保持清晰的逻辑与解决问题的底气。
典型应用场景总结表
| 领域 | 实际问题 | 所用理论/数学工具 | 工程价值 |
|---|---|---|---|
| 模拟电路 | 音频功放失真 | Q点分析、小信号模型 | 提升音质,避免客户投诉 |
| 高频电子 | 手机射频效率低 | 阻抗匹配、S参数、史密斯圆图 | 延长续航,改善通信质量 |
| 电力系统 | 配电网单相接地 | 对称分量法、零序电流检测 | 快速定位故障,减少停电时间 |
| 高速数字设计 | PCIe误码率高 | 传输线理论、TDR、眼图分析 | 保障服务器稳定性 |
| 医疗电子 | ECG工频干扰 | 傅里叶变换、数字滤波器设计 | 辅助临床诊断,挽救生命 |
| 电力电子 | 车载充电机电压过冲 | 状态方程、微分方程求解 | 保护电池安全 |
| 无线通信 | 5G天线增益不足 | 麦克斯韦方程、电磁仿真 | 满足运营商KPI |
| 自动控制 | 无人机抗风性差 | 状态空间、极点配置 | 提升飞行安全性 |