注:本文为 "梯度、散度、旋度" 相关合辑。
图片清晰度受引文原图所限。
略作重排,未整理去重。
如有内容异常,请看原文。
浅谈矢量场 ------ 梯度、散度与拉普拉斯算子
打码的老程 于 2021-03-05 12:56:44 发布
梯度(gradient)
梯度算子的定义与解析式
在引入梯度算子前,首先明确其标准符号表示为 ▽ \triangledown ▽,函数形式为 grad ( f ) \text{grad}(f) grad(f)(简记为 ▽ f \triangledown f ▽f,此处 f f f 特指标量函数)。梯度算子的运算对象是标量函数,其解析式随空间维度不同而变化,具体如下:
1. 二维空间( x − y x-y x−y 平面)
二维场景下,梯度算子的解析式为:
grad ( f ) = ▽ f = ∂ f ∂ x i + ∂ f ∂ y j \text{grad}(f) = \triangledown f = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} grad(f)=▽f=∂x∂fi+∂y∂fj
2. 三维空间( x − y − z x-y-z x−y−z 空间)
三维场景下,梯度算子的解析式为:
grad ( f ) = ▽ f = ∂ f ∂ x i + ∂ f ∂ y j + ∂ f ∂ z k \text{grad}(f) = \triangledown f = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} + \frac{\partial f}{\partial z} \mathbf{k} grad(f)=▽f=∂x∂fi+∂y∂fj+∂z∂fk
其中, i \mathbf{i} i、 j \mathbf{j} j、 k \mathbf{k} k 分别为 x x x、 y y y、 z z z 轴方向的单位向量(通常采用黑体形式标识单位向量)。对于向量分量表达形式不熟悉的读者,可参考线性代数或高等数学教材中关于空间向量分解的相关内容。
由于上述公式为偏微分形式,以 x x x 轴为例,其差分形式可表示为:
∂ f ∂ x = f ( x + Δ x o , y , z ) − f ( x , y , z ) Δ x o \frac{\partial f}{\partial x} = \frac{f(x + \Delta x_o, y, z) - f(x, y, z)}{\Delta x_o} ∂x∂f=Δxof(x+Δxo,y,z)−f(x,y,z)
同理, y y y 轴和 z z z 轴的差分形式分别为:
∂ f ∂ y = f ( x , y + Δ y o , z ) − f ( x , y , z ) Δ y o \frac{\partial f}{\partial y} = \frac{f(x, y + \Delta y_o, z) - f(x, y, z)}{\Delta y_o} ∂y∂f=Δyof(x,y+Δyo,z)−f(x,y,z)
∂ f ∂ z = f ( x , y , z + Δ z o ) − f ( x , y , z ) Δ z o \frac{\partial f}{\partial z} = \frac{f(x, y, z + \Delta z_o) - f(x, y, z)}{\Delta z_o} ∂z∂f=Δzof(x,y,z+Δzo)−f(x,y,z)
差分形式
在计算机应用中,通常令 Δ x o = Δ y o = Δ z o = 1 \Delta x_o = \Delta y_o = \Delta z_o = 1 Δxo=Δyo=Δzo=1,此时常用的差分形式可近似表示为:
∂ f ∂ x ≈ f ( x + 1 , y , z ) − f ( x , y , z ) ∂ f ∂ y ≈ f ( x , y + 1 , z ) − f ( x , y , z ) ∂ f ∂ z ≈ f ( x , y , z + 1 ) − f ( x , y , z ) \frac{\partial f}{\partial x} \approx f(x + 1, y, z) - f(x, y, z)\\[1em] \frac{\partial f}{\partial y} \approx f(x, y + 1, z) - f(x, y, z)\\[1em] \frac{\partial f}{\partial z} \approx f(x, y, z + 1) - f(x, y, z) ∂x∂f≈f(x+1,y,z)−f(x,y,z)∂y∂f≈f(x,y+1,z)−f(x,y,z)∂z∂f≈f(x,y,z+1)−f(x,y,z)
因此,梯度的物理意义为空间中某点分别沿 x x x 轴、 y y y 轴及 z z z 轴方向的斜率。
散度(Divergence)
散度与梯度算子形式相近,符号表示为 ∇ ⋅ F ⃗ \nabla \cdot \vec{F} ∇⋅F ,通常简记为 ∇ ⋅ F \nabla \cdot F ∇⋅F。二者的主要区别在于散度表达式中多一个点乘符号。
数学表达式
散度的解析式为:
div ( F ⃗ ) = ∇ ⋅ F ⃗ = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z \text{div}(\vec{F}) = \nabla \cdot \vec{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} div(F )=∇⋅F =∂x∂Fx+∂y∂Fy+∂z∂Fz
梯度的表达式为:
grad ( f ) = ∇ f = ∂ f ∂ x i + ∂ f ∂ y j + ∂ f ∂ z k \text{grad}(f) = \nabla f = \frac{\partial f}{\partial x} \mathbf{i} + \frac{\partial f}{\partial y} \mathbf{j} + \frac{\partial f}{\partial z} \mathbf{k} grad(f)=∇f=∂x∂fi+∂y∂fj+∂z∂fk
概念转换
通过将标量函数 f f f 与向量分量建立映射关系,可构造向量场:
F ⃗ ( x , y , z ) = x i + y j + z k \vec{F}(x,y,z) = x \mathbf{i} + y \mathbf{j} + z \mathbf{k} F (x,y,z)=xi+yj+zk
此时梯度可转化为散度的等价表达:
∇ ⋅ F ⃗ = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z \nabla \cdot \vec{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} ∇⋅F =∂x∂Fx+∂y∂Fy+∂z∂Fz
主要区别
二者的主要区别体现在观察角度上:

- 梯度:描述在给定欧氏空间坐标系下,空间中某点(如山脊侧面某点)沿坐标轴方向的斜率变化率
- 散度:描述流场中某点的物理量(如速度、密度、热量)的变化率,可通过该点放置的探测装置测量
坐标系分析
从坐标系角度分析:

- 梯度的坐标系为外部固定坐标系,观察点可位于坐标系内任意位置
- 散度的坐标系通常以观察点为中心建立局部 X Y Z XYZ XYZ 坐标系
当梯度的观察点与欧氏空标原点重合时,梯度与散度的表达形式一致。
拉普拉斯算子(Laplace Operator)
拉普拉斯算子,其符号为 △ \triangle △ 或 ▽ 2 \triangledown^2 ▽2,解析式为:
▽ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \triangledown^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} ▽2=∂x2∂2+∂y2∂2+∂z2∂2
拉普拉斯算子描述梯度或散度的变化率,即"变化率的变化率"。经典力学中的加速度公式 v t = v 0 + a t v_t = v_0 + at vt=v0+at 即为该概念的典型应用。
拉普拉斯算子的重要物理意义在于:若假设场在 X Y Z XYZ XYZ 三个分量上的变化均为线性,则可通过该算子直接估算距离测试点 P o P_o Po ( Δ X , Δ Y , Δ Z ) (\Delta X, \Delta Y, \Delta Z) (ΔX,ΔY,ΔZ) 的目标点 P t P_t Pt 处的物理量(如速度、密度、热量等),估算过程与求解加速度的方法类似。
差分形式
其差分形式的近似表达式可由一阶差分推导得出。已知一阶差分形式为:
▽ f ( x ) = f ( x + 1 ) − f ( x ) \triangledown f(x) = f(x + 1) - f(x) ▽f(x)=f(x+1)−f(x)
其二阶差分形式为:
▽ 2 f ( x ) = ▽ f ( x + 1 ) − ▽ f ( x ) \triangledown^2 f(x) = \triangledown f(x + 1) - \triangledown f(x) ▽2f(x)=▽f(x+1)−▽f(x)
将一阶差分代入,可得:
▽ 2 f ( x ) = f ( x + 2 ) − 2 f ( x + 1 ) + f ( x ) \triangledown^2 f(x) = f(x + 2) - 2f(x + 1) + f(x) ▽2f(x)=f(x+2)−2f(x+1)+f(x)
因此,拉普拉斯算子在 X Y Z XYZ XYZ 各方向上的向前差分近似表达式如下:
∂ 2 ∂ x 2 ≈ f ( x + 2 , y , z ) − 2 f ( x + 1 , y , z ) + f ( x , y , z ) ∂ 2 ∂ y 2 ≈ f ( x , y + 2 , z ) − 2 f ( x , y + 1 , z ) + f ( x , y , z ) ∂ 2 ∂ z 2 ≈ f ( x , y , z + 2 ) − 2 f ( x , y , z + 1 ) + f ( x , y , z ) \frac{\partial^2}{\partial x^2} \approx f(x + 2, y, z) - 2f(x + 1, y, z) + f(x, y, z)\\[1em] \frac{\partial^2}{\partial y^2} \approx f(x, y + 2, z) - 2f(x, y + 1, z) + f(x, y, z)\\[1em] \frac{\partial^2}{\partial z^2} \approx f(x, y, z + 2) - 2f(x, y, z + 1) + f(x, y, z) ∂x2∂2≈f(x+2,y,z)−2f(x+1,y,z)+f(x,y,z)∂y2∂2≈f(x,y+2,z)−2f(x,y+1,z)+f(x,y,z)∂z2∂2≈f(x,y,z+2)−2f(x,y,z+1)+f(x,y,z)
理解上述原理后,可自行推导向后差分及中央差分形式的表达式,本文仅作初步介绍。
梯度(gradient)、散度(divergence)与旋度(rotation)
生信小兔 于 2022-08-29 15:14:12 发布
(一)梯度
梯度的定义为:
grad f ( x 1 , x 2 , ... , x n ) = ∂ f ∂ x 1 ∣ P 0 i ^ + ∂ f ∂ x 2 ∣ P 0 j ^ + ⋯ + ∂ f ∂ x n ∣ P 0 k ^ = ( ∂ f ∂ x 1 ∣ P 0 , ∂ f ∂ x 2 ∣ P 0 , ... , ∂ f ∂ x n ∣ P 0 ) \begin{aligned} \text{grad}\ f(x_1, x_2, \dots, x_n) &= \left. \frac{\partial f}{\partial x_1} \right|{P_0} \hat{\mathbf{i}} + \left. \frac{\partial f}{\partial x_2} \right|{P_0} \hat{\mathbf{j}} + \dots + \left. \frac{\partial f}{\partial x_n} \right|{P_0} \hat{\mathbf{k}} \\ &= \left( \left. \frac{\partial f}{\partial x_1} \right|{P_0}, \left. \frac{\partial f}{\partial x_2} \right|{P_0}, \dots, \left. \frac{\partial f}{\partial x_n} \right|{P_0} \right) \end{aligned} grad f(x1,x2,...,xn)=∂x1∂f P0i^+∂x2∂f P0j^+⋯+∂xn∂f P0k^=(∂x1∂f P0,∂x2∂f P0,...,∂xn∂f P0)
其中 f f f 为自变量为 x 1 , x 2 , ... , x n x_1, x_2, \dots, x_n x1,x2,...,xn 的 n n n 元标量函数, i ^ , j ^ , ... , k ^ \hat{\mathbf{i}}, \hat{\mathbf{j}}, \dots, \hat{\mathbf{k}} i^,j^,...,k^ 为各个方向的单位向量, P 0 P_0 P0 表示向量函数定义域内某点。梯度表示该标量函数在 P 0 P_0 P0 点的梯度,为一个向量。因此,标量函数的梯度为向量函数。
示例:
- 二元标量函数 f ( x , y ) = x 2 y 2 f(x, y) = x^2 y^2 f(x,y)=x2y2 的梯度为 grad ( f ) = ( 2 x y 2 , 2 x 2 y ) \text{grad}(f) = (2xy^2, 2x^2y) grad(f)=(2xy2,2x2y)
- 二元标量函数 f ( x , y ) = x 2 + y 2 f(x, y) = x^2 + y^2 f(x,y)=x2+y2 的梯度为 grad ( f ) = ( 2 x , 2 y ) \text{grad}(f) = (2x, 2y) grad(f)=(2x,2y)
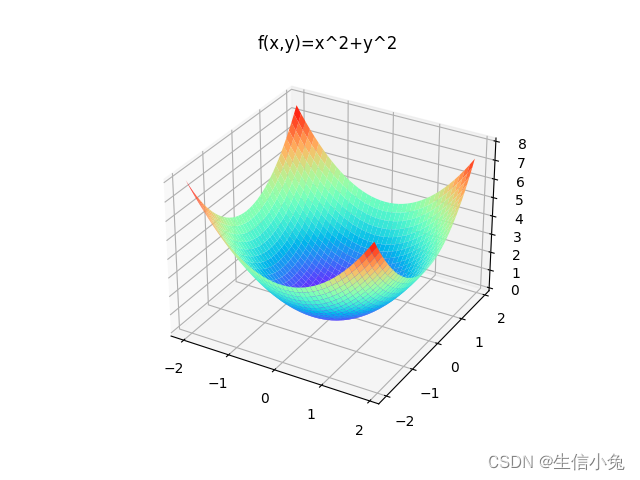

性质 :
标量函数梯度的方向,是该函数在定义域某点处方向导数取得最大值的方向,即函数在该点沿梯度方向的变化最快,变化率最大。
符号表示 :
梯度通常用向量微分算子 ∇ \nabla ∇ 表示, ∇ f \nabla f ∇f 即为标量函数 f f f 的梯度。
注:标量函数的梯度为向量函数。
(二)散度
通量
散度的定义基于通量概念。通量的概念最初源于物理学,在流体运动中,通量是单位时间内流经某单位面积的某属性量,是表征该属性量输送强度的物理量。
在数学中,通量定义为向量函数在某曲面 Σ \Sigma Σ 上的积分:
Φ = ∬ Σ v ( x , y , z ) ⋅ d S = ∬ Σ v ( x , y , z ) ⋅ n ^ d S \Phi = \iint_{\Sigma} \mathbf{v}(x, y, z) \cdot d\mathbf{S} = \iint_{\Sigma} \mathbf{v}(x, y, z) \cdot \hat{\mathbf{n}} dS Φ=∬Σv(x,y,z)⋅dS=∬Σv(x,y,z)⋅n^dS
其中 v ( x , y , z ) = ( P ( x , y , z ) , Q ( x , y , z ) , R ( x , y , z ) ) \mathbf{v}(x, y, z) = (P(x, y, z), Q(x, y, z), R(x, y, z)) v(x,y,z)=(P(x,y,z),Q(x,y,z),R(x,y,z)) 为向量函数, n ^ \hat{\mathbf{n}} n^ 表示 Σ \Sigma Σ 正侧的单位法向量。
散度定义
散度的定义为:
div v ( x , y , z ) = lim Δ V → 0 Δ Φ Δ V = lim Δ V → 0 1 Δ V ∬ Σ v ( x , y , z ) ⋅ n ^ d S \begin{aligned} \text{div}\ \mathbf{v}(x, y, z) &= \lim_{\Delta V \to 0} \frac{\Delta \Phi}{\Delta V} \\ &= \lim_{\Delta V \to 0} \frac{1}{\Delta V} \iint_{\Sigma} \mathbf{v}(x, y, z) \cdot \hat{\mathbf{n}} \, dS \end{aligned} div v(x,y,z)=ΔV→0limΔVΔΦ=ΔV→0limΔV1∬Σv(x,y,z)⋅n^dS
1. 符号说明
- div v \text{div}\ \mathbf{v} div v:向量场 v \mathbf{v} v 的散度,是标量(仅描述大小,无方向)。
- v ( x , y , z ) \mathbf{v}(x,y,z) v(x,y,z):空间向量场(例如流体速度场、电场强度场),其分量形式为 v = ( P , Q , R ) \mathbf{v}=(P,Q,R) v=(P,Q,R)( P 、 Q 、 R P、Q、R P、Q、R 分别对应向量场在 x 、 y 、 z x、y、z x、y、z 轴方向的投影)。
- Δ V \Delta V ΔV:包围点 ( x , y , z ) (x,y,z) (x,y,z) 的微小闭合体积(即体积元)。
- Δ Φ \Delta \Phi ΔΦ:向量场 v \mathbf{v} v 穿过体积 Δ V \Delta V ΔV 边界曲面 Σ \Sigma Σ 的通量 ,具体表达式为 Δ Φ = ∬ Σ v ⋅ n ^ d S \Delta \Phi = \iint_{\Sigma} \mathbf{v} \cdot \hat{\mathbf{n}} dS ΔΦ=∬Σv⋅n^dS。
- Σ \Sigma Σ:包围 Δ V \Delta V ΔV 的闭合曲面(也称为"高斯面"),其正侧约定为曲面外侧。
- n ^ \hat{\mathbf{n}} n^:曲面 Σ \Sigma Σ 上某点的单位法向量,方向垂直于该点曲面,且指向曲面外侧。
- ∬ Σ \iint_{\Sigma} ∬Σ:闭合曲面积分符号,表示积分遍历整个边界曲面 Σ \Sigma Σ。
2. 物理意义
散度的本质是**"单位体积内的通量极限"**:
- 若 div v > 0 \text{div}\ \mathbf{v} > 0 div v>0:该点是向量场的 "源"(如流体从该点向外发散、电场中的正电荷);
- 若 div v < 0 \text{div}\ \mathbf{v} < 0 div v<0:该点是向量场的 "汇"(如流体向该点汇聚、电场中的负电荷);
- 若 div v = 0 \text{div}\ \mathbf{v} = 0 div v=0:该点无汇聚/发散(如无电荷区域的电场、不可压缩流体的无旋流动)。
3. 典型应用
- 流体力学: div v \text{div}\ \mathbf{v} div v 表示流体在某点的"体积膨胀率";
- 电磁学: div E = ρ ε 0 \text{div}\ \mathbf{E} = \frac{\rho}{\varepsilon_0} div E=ε0ρ(高斯定理的微分形式),描述电场在某点的发散程度与电荷密度 ρ \rho ρ 的关系。
散度计算
在空间直角坐标系中,散度可表示为:
div v ( x , y , z ) = ∂ P ( x , y , z ) ∂ x + ∂ Q ( x , y , z ) ∂ y + ∂ R ( x , y , z ) ∂ z \text{div}\ \mathbf{v}(x, y, z) = \frac{\partial P(x, y, z)}{\partial x} + \frac{\partial Q(x, y, z)}{\partial y} + \frac{\partial R(x, y, z)}{\partial z} div v(x,y,z)=∂x∂P(x,y,z)+∂y∂Q(x,y,z)+∂z∂R(x,y,z)
利用该公式即可计算直角坐标系中向量函数的散度。
示例 :
向量函数 v ( x , y ) = ( x 2 , 2 y ) \mathbf{v}(x, y) = (x^2, 2y) v(x,y)=(x2,2y) 的散度为 div v = 2 x + 2 \text{div}\ \mathbf{v} = 2x + 2 div v=2x+2

注:向量函数的散度为标量函数。
(三)旋度
环量
旋度的定义基于环量 (circulation) 概念。在流体力学中,环量是流体速度沿某闭曲线的路径积分;在数学中,环量定义为向量函数沿闭曲线的线积分:
Γ = ∮ L v ( x , y , z ) ⋅ d l \Gamma = \oint_{L} \mathbf{v}(x, y, z) \cdot d\mathbf{l} Γ=∮Lv(x,y,z)⋅dl
环量面密度
环量面密度的定义为:
d Γ d S = lim Δ Σ → M Δ Γ Δ S = lim Δ Σ → M 1 Δ S ∮ Δ L v ( x , y , z ) ⋅ d l \frac{d\Gamma}{dS} = \lim_{\Delta \Sigma \to M} \frac{\Delta \Gamma}{\Delta S} = \lim_{\Delta \Sigma \to M} \frac{1}{\Delta S} \oint_{\Delta L} \mathbf{v}(x, y, z) \cdot d\mathbf{l} dSdΓ=ΔΣ→MlimΔSΔΓ=ΔΣ→MlimΔS1∮ΔLv(x,y,z)⋅dl
其中:
- M M M 为向量场空间中某点
- 在 M M M 点取定方向 n ^ \hat{\mathbf{n}} n^
- Δ Σ \Delta \Sigma ΔΣ 为过点 M M M 且以 n ^ \hat{\mathbf{n}} n^ 为法向量的小曲面
- Δ L \Delta L ΔL 为小曲面的边界曲线
- 曲线的正向与 n ^ \hat{\mathbf{n}} n^ 符合右手规则
旋度定义
旋度的定义为:
rot v ( x , y , z ) = ( ∂ R ∂ y − ∂ Q ∂ z , ∂ P ∂ z − ∂ R ∂ x , ∂ Q ∂ x − ∂ P ∂ y ) = ∇ × v ( x , y , z ) = ∣ i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z P Q R ∣ \begin{aligned} \text{rot}\ \mathbf{v}(x, y, z) &= \left( \frac{\partial R}{\partial y} - \frac{\partial Q}{\partial z}, \frac{\partial P}{\partial z} - \frac{\partial R}{\partial x}, \frac{\partial Q}{\partial x} - \frac{\partial P}{\partial y} \right) \\[1em] &= \nabla \times \mathbf{v}(x, y, z) \\[1em] &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\[1em] \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\[1em] P & Q & R \end{vmatrix} \end{aligned} rot v(x,y,z)=(∂y∂R−∂z∂Q,∂z∂P−∂x∂R,∂x∂Q−∂y∂P)=∇×v(x,y,z)= i^∂x∂Pj^∂y∂Qk^∂z∂R
性质 :
向量函数 v ( x , y , z ) \mathbf{v}(x, y, z) v(x,y,z) 在某点 M M M 的旋度:
- 方向为环量面密度取得最大值的方向
- 模为环量面密度的最大值
注:向量函数的旋度为向量函数。
散度、梯度、旋度及其衍生
eriis 已于 2024-09-18 20:42:35 修改
倒三角算符
倒三角算符(记为 ∇ \nabla ∇),称为 nabla 算符、哈密顿算符或 del 算符,其表达式为:
∇ = i ^ ∂ ∂ x + j ^ ∂ ∂ y + k ^ ∂ ∂ z \nabla = \hat{\mathbf{i}} \frac{\partial}{\partial x} + \hat{\mathbf{j}} \frac{\partial}{\partial y} + \hat{\mathbf{k}} \frac{\partial}{\partial z} ∇=i^∂x∂+j^∂y∂+k^∂z∂
在向量微积分中, ∇ \nabla ∇ 用作三个不同微分算子的组成部分:
- 梯度( ∇ f \nabla f ∇f)
- 散度( ∇ ⋅ F \nabla \cdot \mathbf{F} ∇⋅F)
- 旋度( ∇ × F \nabla \times \mathbf{F} ∇×F)
一阶组合形式
梯度
梯度表示表示某标量在空间某一位置沿某一方向的变化率。
在表现形式上是倒三角算符乘一个标量,得到一个新的矢量。
∇ f = ∂ f ∂ x i ^ + ∂ f ∂ y j ^ + ∂ f ∂ z k ^ \nabla f = \frac{\partial f}{\partial x} \hat{\mathbf{i}} + \frac{\partial f}{\partial y} \hat{\mathbf{j}} + \frac{\partial f}{\partial z} \hat{\mathbf{k}} ∇f=∂x∂fi^+∂y∂fj^+∂z∂fk^
散度
散度表征场的有源性。
在表现形式上是倒三角算符点乘一个矢量,得到的结果是一个标量。
div F = ∇ ⋅ F = ∂ F x ∂ x + ∂ F y ∂ y + ∂ F z ∂ z \text{div}\ \mathbf{F} = \nabla \cdot \mathbf{F} = \frac{\partial F_x}{\partial x} + \frac{\partial F_y}{\partial y} + \frac{\partial F_z}{\partial z} div F=∇⋅F=∂x∂Fx+∂y∂Fy+∂z∂Fz
注意:散度运算为点积,梯度运算为算符直接作用于标量,二者符号表达存在明确差异。
旋度
旋度在表现形式上为倒三角算符叉乘一个矢量,得到的结果是一个矢量。
∇ × F = ∣ i ^ j ^ k ^ ∂ ∂ x ∂ ∂ y ∂ ∂ z F x F y F z ∣ = ( ∂ F z ∂ y − ∂ F y ∂ z ) i ^ + ( ∂ F x ∂ z − ∂ F z ∂ x ) j ^ + ( ∂ F y ∂ x − ∂ F x ∂ y ) k ^ \begin{aligned} \nabla \times \mathbf{F} &= \begin{vmatrix} \hat{\mathbf{i}} & \hat{\mathbf{j}} & \hat{\mathbf{k}} \\[1em] \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\[1em] F_x & F_y & F_z \end{vmatrix} \\ &= \left( \frac{\partial F_z}{\partial y} - \frac{\partial F_y}{\partial z} \right) \hat{\mathbf{i}} + \left( \frac{\partial F_x}{\partial z} - \frac{\partial F_z}{\partial x} \right) \hat{\mathbf{j}} + \left( \frac{\partial F_y}{\partial x} - \frac{\partial F_x}{\partial y} \right) \hat{\mathbf{k}} \end{aligned} ∇×F= i^∂x∂Fxj^∂y∂Fyk^∂z∂Fz =(∂y∂Fz−∂z∂Fy)i^+(∂z∂Fx−∂x∂Fz)j^+(∂x∂Fy−∂y∂Fx)k^
二阶组合形式
在上述三度的基础上,可以进一步进行处理。比如散度的梯度、梯度的散度等等。
它们的二阶形式一共有 5 种,下文对两个易于混淆的进行解释。
梯度的散度(拉普拉斯算符)
标量经梯度运算后得到向量,该向量可进一步进行散度运算,最终结果为标量:
∇ ⋅ ( ∇ T ) = ( x ^ ∂ ∂ x + y ^ ∂ ∂ y + z ^ ∂ ∂ z ) ⋅ ( ∂ T ∂ x x ^ + ∂ T ∂ y y ^ + ∂ T ∂ z z ^ ) = ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ∂ 2 T ∂ z 2 \begin{aligned} \nabla \cdot (\nabla T) &= \left( \hat{\mathbf{x}} \frac{\partial}{\partial x} + \hat{\mathbf{y}} \frac{\partial}{\partial y} + \hat{\mathbf{z}} \frac{\partial}{\partial z} \right) \cdot \left( \frac{\partial T}{\partial x}\hat{\mathbf{x}} + \frac{\partial T}{\partial y}\hat{\mathbf{y}} + \frac{\partial T}{\partial z}\hat{\mathbf{z}} \right) \\ &= \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \end{aligned} ∇⋅(∇T)=(x^∂x∂+y^∂y∂+z^∂z∂)⋅(∂x∂Tx^+∂y∂Ty^+∂z∂Tz^)=∂x2∂2T+∂y2∂2T+∂z2∂2T
向量点积的规则是"对应分量相乘后求和",且单位向量满足:
- 同方向单位向量点积为 1,例如 x ^ ⋅ x ^ = 1 \hat{\mathbf{x}} \cdot \hat{\mathbf{x}} = 1 x^⋅x^=1
- 不同方向单位向量点积为 0,例如 x ^ ⋅ y ^ = 0 \hat{\mathbf{x}} \cdot \hat{\mathbf{y}} = 0 x^⋅y^=0
拉普拉斯算符 :
上述计算过程可引入拉普拉斯算符进行简化:
∇ ⋅ ( ∇ s ) = ∇ 2 s = ∂ 2 s ∂ x 2 + ∂ 2 s ∂ y 2 + ∂ 2 s ∂ z 2 \nabla\cdot(\nabla s)=\nabla^2 s = \frac{\partial^2 s}{\partial x^2} + \frac{\partial^2 s}{\partial y^2} + \frac{\partial^2 s}{\partial z^2} ∇⋅(∇s)=∇2s=∂x2∂2s+∂y2∂2s+∂z2∂2s
向量拉普拉斯算符:
This object, which we write as ∇ 2 T \nabla^2 T ∇2T for short, is called the Laplacian of T T T; we shall be studying it in great detail later on. Notice that the Laplacian of a scalar T T T is a scalar. Occasionally, we shall speak of the Laplacian of a vector , ∇ 2 v \nabla^2 \mathbf{v} ∇2v. By this we mean a vector quantity whose x x x-component is the Laplacian of v x v_x vx, and so on:
这个对象,我们简称为 ∇ 2 T \nabla^2 T ∇2T,被称为 T T T 的拉普拉斯算子 ;我们将在后面详细研究它。请注意,一个标量 T T T 的拉普拉斯算子是一个标量。有时,我们会提到一个矢量 的拉普拉斯算子, ∇ 2 v \nabla^2 \mathbf{v} ∇2v。我们指的是一个矢量量,其 x x x 分量是 v x v_x vx 的拉普拉斯算子,依此类推:
∇ 2 v ≡ ( ∇ 2 v x ) x ^ + ( ∇ 2 v y ) y ^ + ( ∇ 2 v z ) z ^ . \nabla^2 \mathbf{v} \equiv (\nabla^2 v_x) \hat{\mathbf{x}} + (\nabla^2 v_y) \hat{\mathbf{y}} + (\nabla^2 v_z) \hat{\mathbf{z}}. ∇2v≡(∇2vx)x^+(∇2vy)y^+(∇2vz)z^.
在三维笛卡尔坐标系中,拉普拉斯算子定义为:
∇ 2 = ∂ 2 ∂ x 2 + ∂ 2 ∂ y 2 + ∂ 2 ∂ z 2 \nabla^2 = \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} + \frac{\partial^2}{\partial z^2} ∇2=∂x2∂2+∂y2∂2+∂z2∂2
-
标量场 :对于一个标量场 T ( x , y , z ) T(x, y, z) T(x,y,z),拉普拉斯算子的作用是计算该标量场的二阶偏导数之和,即:
∇ 2 T = ∂ 2 T ∂ x 2 + ∂ 2 T ∂ y 2 + ∂ 2 T ∂ z 2 \nabla^2 T = \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} ∇2T=∂x2∂2T+∂y2∂2T+∂z2∂2T
这表示标量场在空间中每一点的"曲率"或"凹凸性"。
-
矢量场 :虽然拉普拉斯算子通常用于标量场,但它也可以应用于矢量场的每个分量。对于矢量场 v = v x x ^ + v y y ^ + v z z ^ \mathbf{v} = v_x \hat{\mathbf{x}} + v_y \hat{\mathbf{y}} + v_z \hat{\mathbf{z}} v=vxx^+vyy^+vzz^,拉普拉斯算子作用于矢量场的表达式为:
∇ 2 v = ( ∂ 2 v x ∂ x 2 + ∂ 2 v x ∂ y 2 + ∂ 2 v x ∂ z 2 ) x ^ + ( ∂ 2 v y ∂ x 2 + ∂ 2 v y ∂ y 2 + ∂ 2 v y ∂ z 2 ) y ^ + ( ∂ 2 v z ∂ x 2 + ∂ 2 v z ∂ y 2 + ∂ 2 v z ∂ z 2 ) z ^ \nabla^2 \mathbf{v} = \left( \frac{\partial^2 v_x}{\partial x^2} + \frac{\partial^2 v_x}{\partial y^2} + \frac{\partial^2 v_x}{\partial z^2} \right) \hat{\mathbf{x}} + \left( \frac{\partial^2 v_y}{\partial x^2} + \frac{\partial^2 v_y}{\partial y^2} + \frac{\partial^2 v_y}{\partial z^2} \right) \hat{\mathbf{y}} + \left( \frac{\partial^2 v_z}{\partial x^2} + \frac{\partial^2 v_z}{\partial y^2} + \frac{\partial^2 v_z}{\partial z^2} \right) \hat{\mathbf{z}} ∇2v=(∂x2∂2vx+∂y2∂2vx+∂z2∂2vx)x^+(∂x2∂2vy+∂y2∂2vy+∂z2∂2vy)y^+(∂x2∂2vz+∂y2∂2vz+∂z2∂2vz)z^
这表示矢量场每个分量的局部变化情况。
在 Mathematical Methods for Physicists (7th Ed) 中对此作出如下解释:拉普拉斯算子 ∇ 2 \nabla^2 ∇2 对于标量的作用结果仍为标量。不过,有时会将拉普拉斯算子作用于向量,此时需对该矢量的三个分量分别应用拉普拉斯算子。
例如纳维-斯托克斯(N-S)方程中即存在该算子作用于矢量的实例:
∂ V ∂ t + ( V ∙ ∇ ) V = f − 1 ρ ∇ p + μ ρ ∇ 2 V \frac{\partial \boldsymbol{V}}{\partial t} + (\boldsymbol{V} \bullet \nabla) \boldsymbol{V} = \boldsymbol{f} - \frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \nabla^2 \boldsymbol{V} ∂t∂V+(V∙∇)V=f−ρ1∇p+ρμ∇2V
此外,在纳维-斯托克斯(N-S)方程中常可见矢量点乘哈密顿算子的用法,这一表述虽易引发困惑,但实际上是一种约定俗成的表达方式。
需要特别说明的是,算子 ∇ \nabla ∇ 并非真正的矢量,仅是一个运算符号;因此 ∇ ⋅ A \nabla \cdot \boldsymbol{A} ∇⋅A 与 A ⋅ ∇ \boldsymbol{A} \cdot \nabla A⋅∇ 并不相等, A ⋅ ∇ \boldsymbol{A} \cdot \nabla A⋅∇ 仅表示如下微分算子:
A ⋅ ∇ = A x ∂ ∂ x + A y ∂ ∂ y + A z ∂ ∂ z \boldsymbol{A} \cdot \nabla = A_x \frac{\partial}{\partial x} + A_y \frac{\partial}{\partial y} + A_z \frac{\partial}{\partial z} A⋅∇=Ax∂x∂+Ay∂y∂+Az∂z∂
在 Mathematical Methods for Physicists(7th Ed) 中对此做出了解释:拉普拉斯算子对于标量的结果是标量。然而,有时会用拉普拉斯算子求向量,此时相对于对该矢量的三个分量分别使用拉普拉斯算子。
例如 纳维-斯托克斯方程( N-S 方程)中的就有对矢量应用的例子
∂ V ∂ t + ( V ⋅ ∇ ) V = f − 1 ρ ∇ p + μ ρ ∇ 2 V \frac{\partial \mathbf{V}}{\partial t} + (\mathbf{V} \cdot \nabla) \mathbf{V} = \mathbf{f} - \frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \nabla^2 \mathbf{V} ∂t∂V+(V⋅∇)V=f−ρ1∇p+ρμ∇2V
注意 : ∇ \nabla ∇ 并非真实向量,仅为运算符号,因此 ∇ ⋅ A ≠ A ⋅ ∇ \nabla \cdot \mathbf{A} \neq \mathbf{A} \cdot \nabla ∇⋅A=A⋅∇。其中:
A ⋅ ∇ = A x ∂ ∂ x + A y ∂ ∂ y + A z ∂ ∂ z \mathbf{A} \cdot \nabla = A_x \frac{\partial}{\partial x} + A_y \frac{\partial}{\partial y} + A_z \frac{\partial}{\partial z} A⋅∇=Ax∂x∂+Ay∂y∂+Az∂z∂
散度的梯度
一个矢量经过散度计算,结果是一个标量;该标量仍可进行梯度计算,最终得到一个矢量。此运算在物理问题中较少出现,此处说明是为了避免其与拉普拉斯算子混淆。
事实上,散度的梯度表述如下:
Divergence of gradient: ∇ ⋅ ( ∇ T ) \nabla \cdot (\nabla T) ∇⋅(∇T)。
Hence:因此:
grad ( div V ) = ∇ ( ∇ ⋅ V ) = ( i ∂ ∂ x + j ∂ ∂ y + k ∂ ∂ z ) ( ∂ V x ∂ x + ∂ V y ∂ y + ∂ V z ∂ z ) = ( ∂ 2 V x ∂ x 2 + ∂ 2 V y ∂ x ∂ y + ∂ 2 V z ∂ x ∂ z ) i + ( ∂ 2 V x ∂ x ∂ y + ∂ 2 V y ∂ y 2 + ∂ 2 V z ∂ y ∂ z ) j + ( ∂ 2 V x ∂ x ∂ z + ∂ 2 V y ∂ y ∂ z + ∂ 2 V z ∂ z 2 ) k \begin{aligned} \operatorname{grad}(\operatorname{div} \boldsymbol{V}) &= \nabla (\nabla \cdot \boldsymbol{V}) \\ &= \left( \boldsymbol{i} \frac{\partial}{\partial x} + \boldsymbol{j} \frac{\partial}{\partial y} + \boldsymbol{k} \frac{\partial}{\partial z} \right) \left( \frac{\partial V_x}{\partial x} + \frac{\partial V_y}{\partial y} + \frac{\partial V_z}{\partial z} \right) \\ &= \left( \frac{\partial^2 V_x}{\partial x^2} + \frac{\partial^2 V_y}{\partial x \partial y} + \frac{\partial^2 V_z}{\partial x \partial z} \right) \boldsymbol{i} + \left( \frac{\partial^2 V_x}{\partial x \partial y} + \frac{\partial^2 V_y}{\partial y^2} + \frac{\partial^2 V_z}{\partial y \partial z} \right) \boldsymbol{j} + \left( \frac{\partial^2 V_x}{\partial x \partial z} + \frac{\partial^2 V_y}{\partial y \partial z} + \frac{\partial^2 V_z}{\partial z^2} \right) \boldsymbol{k} \end{aligned} grad(divV)=∇(∇⋅V)=(i∂x∂+j∂y∂+k∂z∂)(∂x∂Vx+∂y∂Vy+∂z∂Vz)=(∂x2∂2Vx+∂x∂y∂2Vy+∂x∂z∂2Vz)i+(∂x∂y∂2Vx+∂y2∂2Vy+∂y∂z∂2Vz)j+(∂x∂z∂2Vx+∂y∂z∂2Vy+∂z2∂2Vz)k
散度的梯度
向量经散度运算后得到标量,该标量可进一步进行梯度运算,最终结果为向量:
∇ ( ∇ ⋅ V ) = ( ∂ 2 V x ∂ x 2 + ∂ 2 V y ∂ x ∂ y + ∂ 2 V z ∂ x ∂ z ) i ^ + ( ∂ 2 V x ∂ x ∂ y + ∂ 2 V y ∂ y 2 + ∂ 2 V z ∂ y ∂ z ) j ^ + ( ∂ 2 V x ∂ x ∂ z + ∂ 2 V y ∂ y ∂ z + ∂ 2 V z ∂ z 2 ) k ^ \nabla (\nabla \cdot \mathbf{V}) = \left( \frac{\partial^2 V_x}{\partial x^2} + \frac{\partial^2 V_y}{\partial x \partial y} + \frac{\partial^2 V_z}{\partial x \partial z} \right) \hat{\mathbf{i}} + \left( \frac{\partial^2 V_x}{\partial x \partial y} + \frac{\partial^2 V_y}{\partial y^2} + \frac{\partial^2 V_z}{\partial y \partial z} \right) \hat{\mathbf{j}} + \left( \frac{\partial^2 V_x}{\partial x \partial z} + \frac{\partial^2 V_y}{\partial y \partial z} + \frac{\partial^2 V_z}{\partial z^2} \right) \hat{\mathbf{k}} ∇(∇⋅V)=(∂x2∂2Vx+∂x∂y∂2Vy+∂x∂z∂2Vz)i^+(∂x∂y∂2Vx+∂y2∂2Vy+∂y∂z∂2Vz)j^+(∂x∂z∂2Vx+∂y∂z∂2Vy+∂z2∂2Vz)k^
爱因斯坦求和约定
爱因斯坦求和约定(Einstein summation convention)就是省略求和式中的求和符号。
该规则规定:在同一项中,若同一指标(称为"哑指标")成对出现,则表示遍历该指标的取值范围并求和。
示例 :
不可压缩流体的连续性方程:
∂ u i ∂ x i = 0 \frac{\partial u_i}{\partial x_i} = 0 ∂xi∂ui=0
其中指标 i i i 的取值范围为 1 ∼ 3 1 \sim 3 1∼3,该式通过爱因斯坦求和约定省略了求和符号。
via:
-
浅谈矢量场 ------ 梯度、散度与拉普拉斯算子_拉普拉斯算子和梯度算子的关系-CSDN博客
https://blog.csdn.net/poisonchry/article/details/114387703 -
梯度(gradient)、散度(divergence)与旋度(rotation)_梯度散度旋度-CSDN博客
https://blog.csdn.net/weixin_60737527/article/details/126573106 -
【前置知识】散度、梯度、旋度及其衍生_梯度散度旋度-CSDN博客
https://blog.csdn.net/a5567899/article/details/137194466 -
基础数学系列:梯度、散度、旋度 - 知乎
https://zhuanlan.zhihu.com/p/718713293