一、1位计数器:

综合后Schematic:
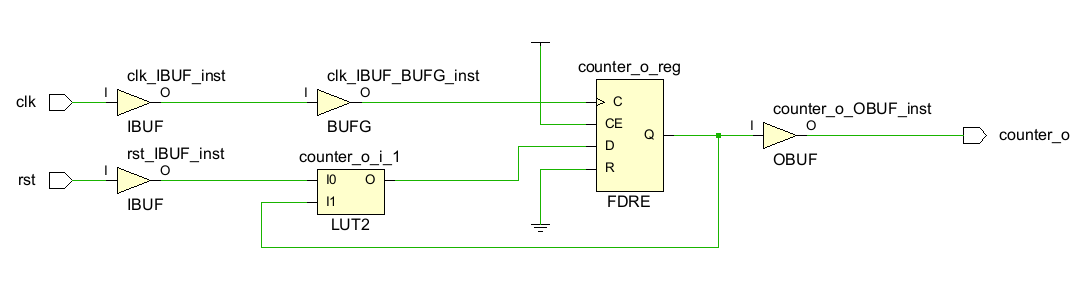
1位计数器综合后的主要结构为一个LUT2查找表和一个D触发器,其中LUT2的INIT值为4'b0001,因此只有当rst为0且触发器的输出Q为0时LUT2的输出才为1,即Q在下个时钟周期的输出为1,LUT2的输出为0,Q在第二个时钟周期的输出为0,以 0-1-0-1 的规律循环。
二、2位计数器

综合后Schematic: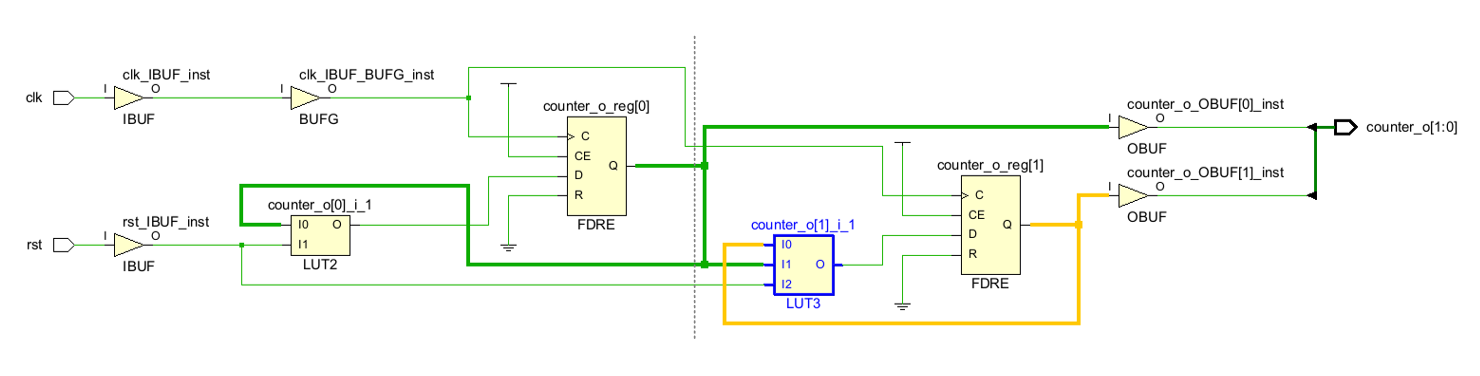
2位计数器综合后主要结构为一个LUT2查找表(INIT=4'h1)、一个LUT3查找表(INIT=8'h06)和2个D触发器。电路前半部分即为1位计数器;对于LUT3,只有当I1⨁I0=1时输出才为1,如下表所示,因此counter的值按00-01-10-11的规律变化。
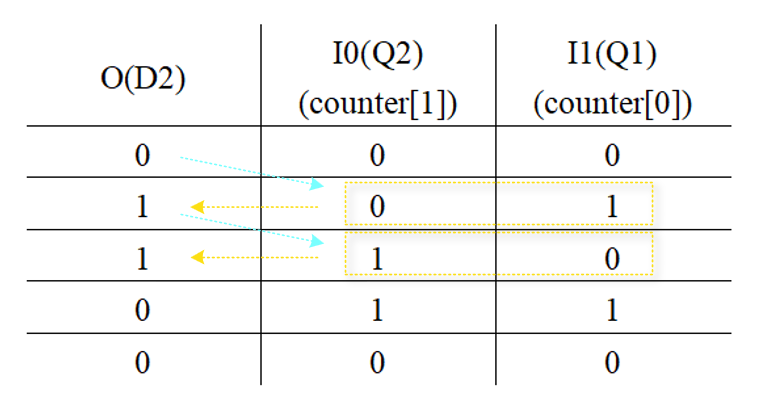
三、3位计数器

综合后Schematic:
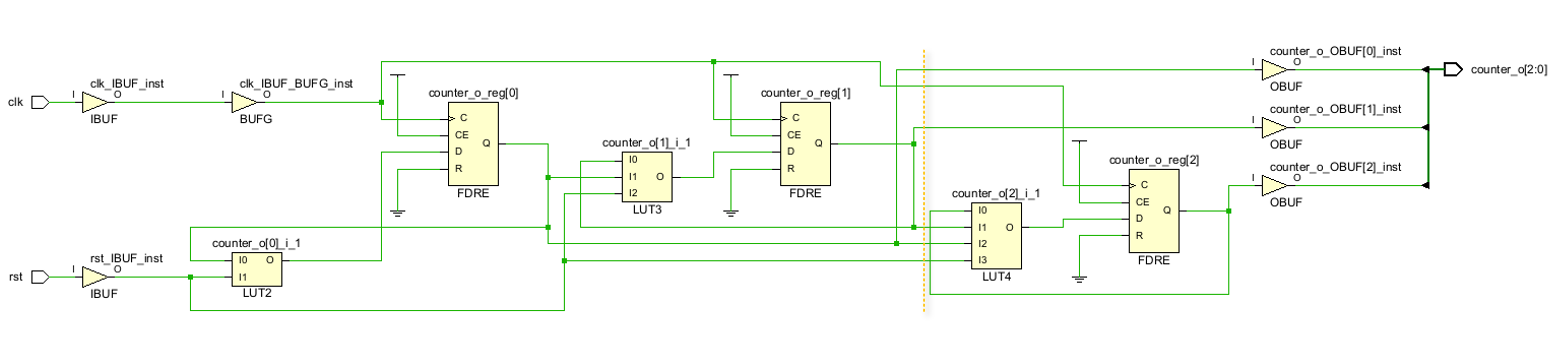
3位计数器综合后主要结构为一个LUT2查找表(INIT=4'h1)、一个LUT3查找表(INIT=8'h06)、一个LUT4查找表(INIT=16'h006A)和3个D触发器。电路前半部分即为2位计数器;对于LUT4,只有当 { I2,I1,I0 } =1、3、5、6时输出才为1,如下表所示,因此counter的值按000-001...110-111的规律变化。
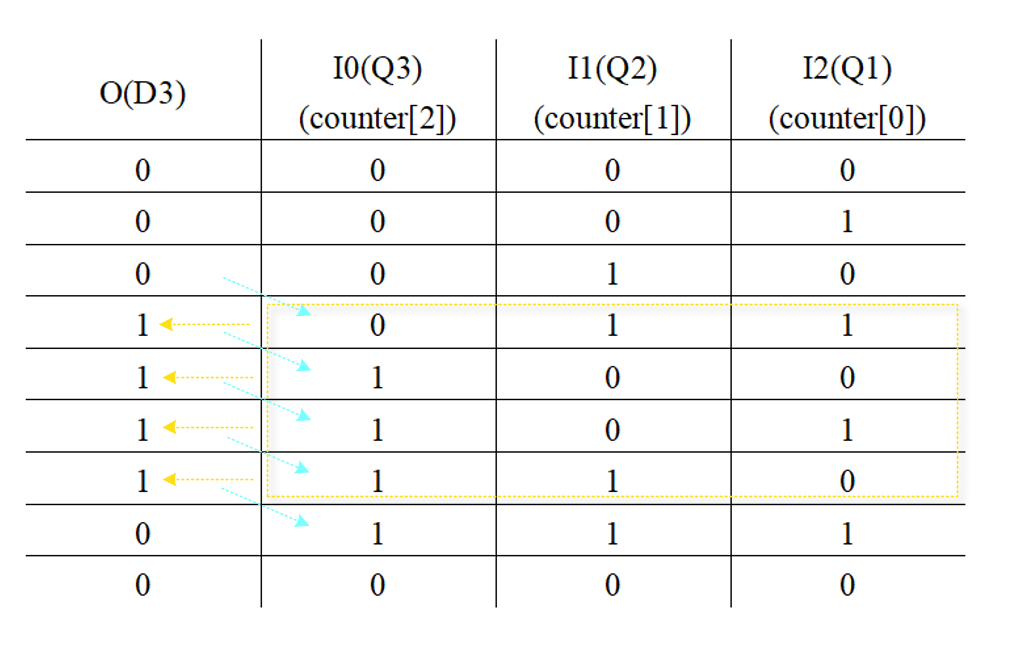
根据以上分析我们可以大致找到计数器综合后电路随位数变化的规律,并发现计数器位数越多延迟越大,并且每位延迟随位数增大而增大,如第0位延迟最小(约1个LUT和1个D触发器),最高位N延迟最大,可能需要N个LUT和N个D触发器的延迟,这将限制计数器的速度。
加法器的设计与之类似,一个N位加法器可以通过把N个一位的全加器(FA)电路串联起来构成,即对于从k=1至N-1把Co(k-1)连接到Ci(k),并使第一个输人进位Ci连接至0。这一结构称为逐位进位加法器或行波进位加法器,因为进位位从一级"波动"到另一级。通过该电路的延时取决于传播必须通过的逻辑级的数目并且与所加的输人信号有关。进位必须从最低有效位一直波动到最高有效位这样一个结构(也称为关键路径)的传播延时定义为对所有可能的输入图形在最坏情形下的延时。
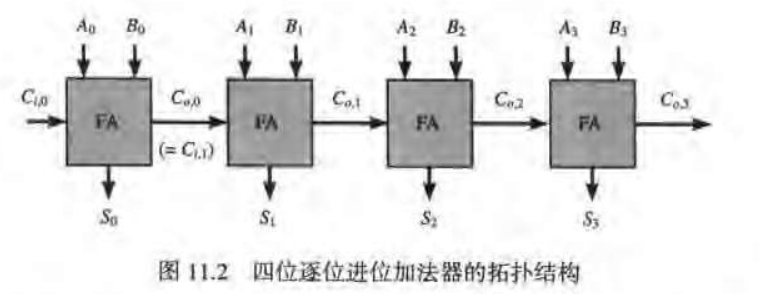
由于逐位进位加法器的传播延时与N成线性关系,在设计更快速的加法器时,避免逐级进位效应至关重要。超前进位原理提供了一种有可能解决这个问题的方法。
从实现的角度把S和Co定义为某些中间信号G(进位产生,generate)和D(进位取消,delete)和P(进位传播,propagate)的函数是非常有用的。G=1/D=1时,将保证在Co产生/取消一个进位,而与Ci无关,而P=1时将保证有一个进位输入传播至Co。这些信号的表达式可以通过观察真值表推导出来:
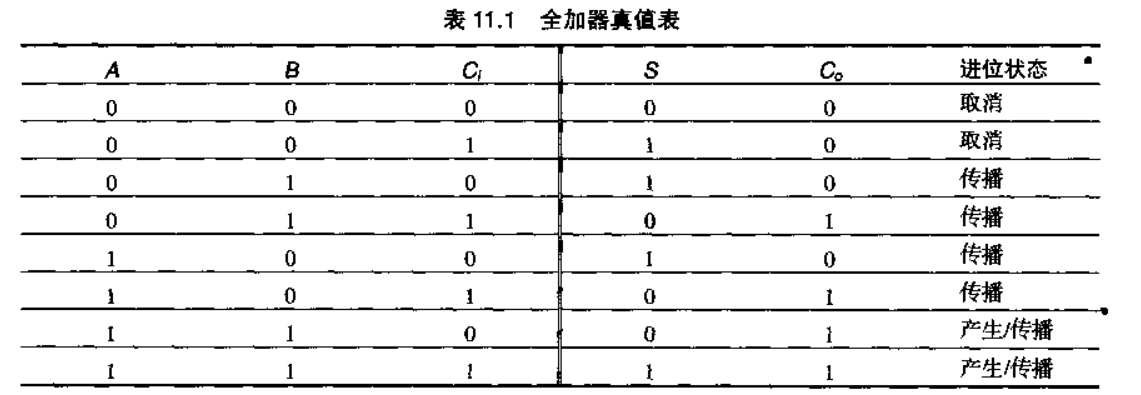
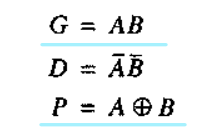
根据S和Co的表达式:
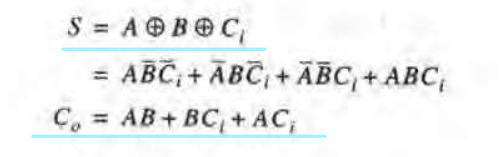
可以得到:
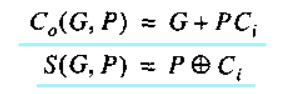
且G和P仅是A和B的函数而与Ci无关。
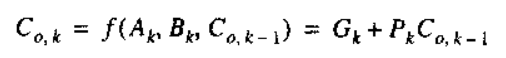
通过展升Co(k-1)可以消除Co(k)对Co(k-1)的依赖联系,其中Ci(0)通常为0:
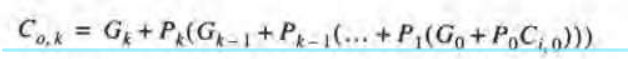
即当前位进位等于当前位进位产生(AB=1)或上一位的进位传播(A⨁B=1),并且两者不会同时为1。例如对于四位全加器:

现在我们对16位的计数器进行综合,得到Schematic如下,可以发现电路中出现了四个CARRY4模块:
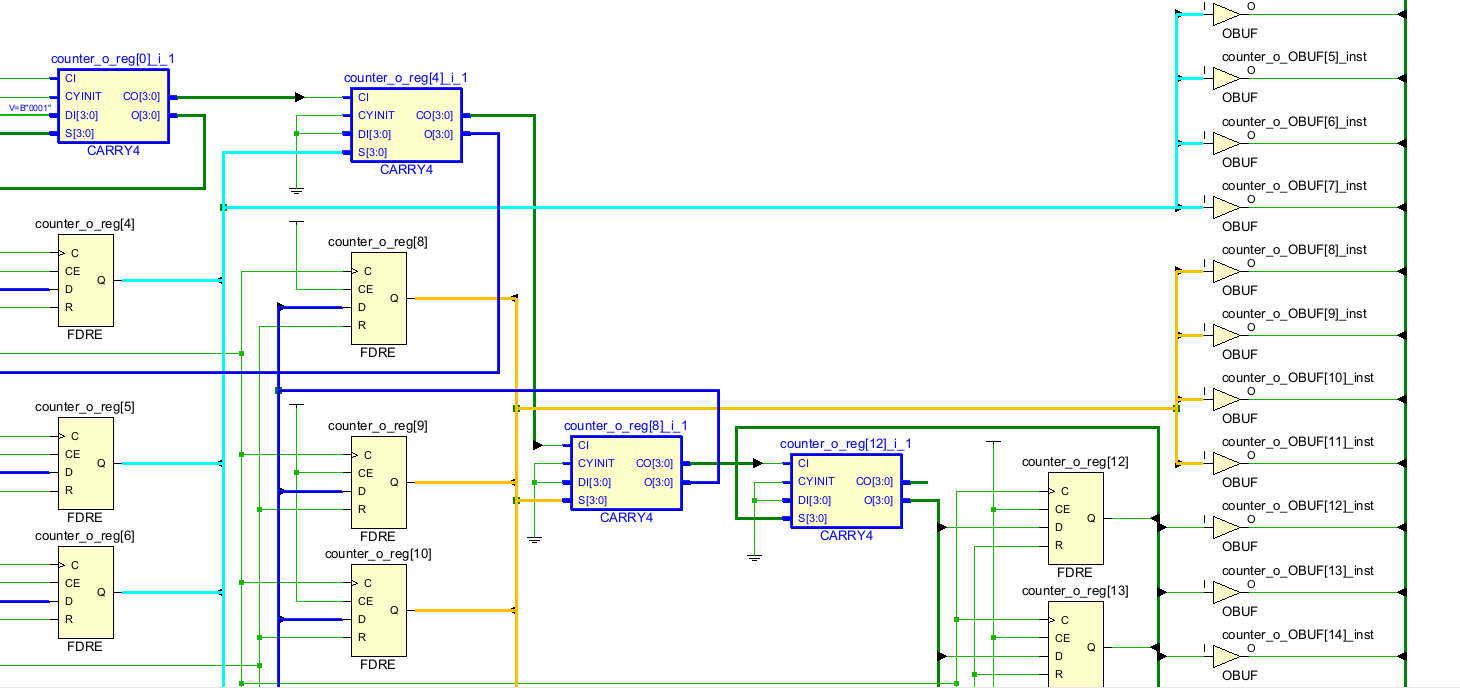
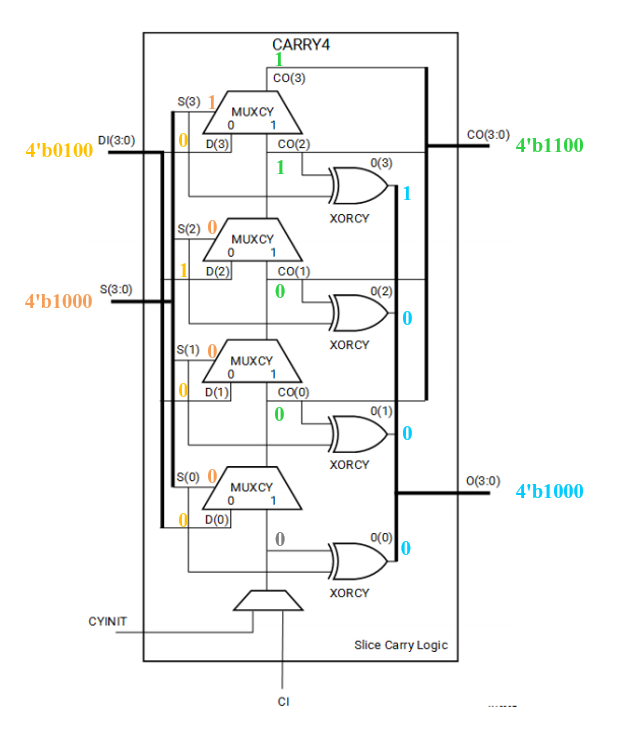
CARRY4 是Xilinx FPGA中的一种进位逻辑单元,用于实现快速的加法和减法运算。它是超前进位加法器 的一种实现方式,能够在FPGA中实现高效的算术运算。CARRY4原语结构如下,输入S为A⨁B,DI为A或者B,以及上一级进位Ci;输出为每位的进位Co和最终和O。
这里我们以加数A=4'b0100和被加数B=4'b1100为例,S=A⨁B=4'b1000,DI可以选择A或B,这里选择A。观察结构图发现,S作为MUX的选通信号,当S=1时,P=A⨁B=1,进位传播, 选择CO(k-1)作为当前位的CO(k)输出;当S=0时,A⨁B=0,即A=B=0或A=B=1,选择DI作为当前位的进位输出。这是因为若A=B=0,D=A'B'=1,进位取消, Co=A=B=0**;若A=B=1,G=AB=1,进位产生** ,Co=A=B=1**。** 而和输出O=S⨁Ci。