LFM线性调频和脉冲压缩的理论总结与仿真

阿源-2025-11-26 17:26

一、背景

使用雷达探测物体时，雷达发射电磁波，电磁波撞到物体后反射回来，雷达接收回波信号来判断物体的位置。想象一下，如果雷达发出的信号非常弱，信号还没有到达物体处或者回波还没回来就衰减差不多了，雷达就探测不到物体的位置。雷达发射信号的功率有限，那么如果要提高信号的总能量，就只能增加信号的持续时间。

这样是能探测到物体了，但是如果两个物体离得很近会发生什么呢。雷达发出的微波信号，在碰到第一个物体时返回，过一段时间碰到第二个物体的信号也会返回。由于回波信号的时间很长，雷达信号在接收第一个回波信号的过程中，第二个回波信号又来了，这就会造成两个信号叠加，雷达无法分辨出这两个距离过近的物体。

对于以上说明的情况来说，远距离探测和高分辨率是一对矛盾点。那么有没有什么方法，能够一定程度上在探测距离和分辨率指标上都有能有较好的表现呢，线性调频和脉冲压缩就是为了解决这个问题。

二、线性调频信号

顾名思义，线性调频信号（LFM）的瞬时频率随时间线性变化，频率\(f\)与时间\(t\)的关系和表示为

\[f(t) = f_c + K \cdot t \]

其中：

  • \(f_c\) 是脉冲的中心频率。
  • \(K\) 是调频率（或称啁啾率），表示频率变化的速度，单位是 \(\text{Hz/s}\)。
  • \(K = \frac{B}{T}\)，其中 \(B\) 是带宽， \(T\) 是脉冲宽度。

LFM 信号的数学表达式可以写作

\[s(t) = \text{rect}\left(\frac{t}{T}\right) \cdot e^{j 2 \pi (f_c t + \frac{1}{2} K t^2)} \]

其中 \(\text{rect}(\frac{t}{T})\) 是一个矩形窗函数，表示信号的时宽为 \(T\)。

\[\text{rect}(t) = \begin{cases} 1 & \text{if } |t| < \frac{1}{2} \\ \frac{1}{2} & \text{if } |t| = \frac{1}{2} \\ 0 & \text{if } |t| > \frac{1}{2} \end{cases} \]

LFM 具有长时宽（T）和大带宽（B）的特点。长时宽意味着可以在保持峰值功率较低的同时，注入更多的总能量 ，从而提高雷达的作用距离（探测灵敏度）。大带宽能够提高雷达的距离分辨率

\[\Delta R \propto \frac{c}{2B} \]

这个结论记住就好，即带宽越大，距离分辨力越好，下面会进行推导。

LFM 信号的优势在于它将长时宽（高能量） 和**大带宽（高分辨率）**这两个通常相互矛盾的指标结合起来。

三、脉冲压缩

脉冲压缩是一种信号处理技术，它允许雷达在发射长脉冲（高能量）的同时，获得短脉冲（高分辨率）的效果。它通过对回波信号进行匹配滤波来实现。

首先雷达接收到目标反射回来的长 LFM 脉冲 \(r(t)\)。

然后需要对接收到的 \(r(t)\) 进行匹配滤波，其被输入到一个匹配滤波器中，这个滤波器的冲激响应 \(h(t)\) 是发射 LFM 信号 \(s(t)\) 的时间反转和共轭：

\[h(t) = s^*(T - t) \]

匹配滤波器的输出 \(y(t)\) 是输入信号 \(r(t)\) 与滤波器冲激响应 \(h(t)\) 的卷积：

\[y(t) = r(t) * h(t) \]

由于 \(h(t)\) 是 \(s(t)\) 的匹配滤波器，当回波信号 \(r(t)\) 与其匹配滤波器卷积时，输出信号的能量会被集中到时间轴上的一个非常窄的尖峰中。

  • 压缩前的脉宽： \(T\) (长时宽)
  • 压缩后的脉宽： \(\tau \approx \frac{1}{B}\) (窄时宽)

脉冲压缩带来的性能提升由时间带宽积 (Time-Bandwidth Product, TB) 决定。

四、LFM 表达式用复数的原因

现实世界中的信号只有实数，没有复数，因此使用复数作为信号表达式本质上是一种数学技巧，目的是更加便于分析处理信号。

在雷达或通信系统中实际发射接收到的信号，比如一个随时间变化的电压，肯定是实数，比如说

\[S_{real}(t)=rect(\frac{t}{T}cos(2\pi f_c t + \pi K t^2)) \]

这个才是物理上真正存在的信号。

余弦函数虽然直观，但它有两个"隐藏成分"：正频率和负频率。而且当你做傅里叶变换、滤波、匹配滤波、时频分析等操作时，余弦会让公式变得又长又复杂，还容易出错。比如，如果你对 cos(θ ) 做傅里叶变换，你会得到两个冲激------一个在正频率，一个在负频率。但在很多工程应用中（比如雷达），我们其实只关心正频率部分，因为负频率是数学产物，没有物理意义。

复数表示只保留有用的一半。复指数信号在数学上有个神奇的性质：它的傅里叶变换只出现在正频率。这就相当于把余弦"拆开"，只取我们关心的那一半（称为解析信号或复包络）。这样做的好处是

  1. 计算简单：导数、积分、卷积、傅里叶变换都更容易。
  2. 避免负频率干扰：专注处理正频率，符合实际系统带通特性。
  3. 便于调制解调建模：现代通信和雷达系统普遍用"复基带模型"，把高频载波去掉，只处理低频的复包络，大大简化设计。

我们在仿真或理论分析时用复数形式，但在真正发射信号前，会取它的实部。所以复数只是中间工具，最终还是要回到实数世界。

五、距离分辨率推导

先定性分析一下。

  • 如果你发射一个纯正弦波 （比如连续波，带宽 B ≈0），那它看起来"平平无奇"，持续很久都一样，你根本没法判断回波是早到 1 纳秒还是晚到 1 纳秒------分辨率极差。
  • 但如果你发射一个变化剧烈的信号 （比如一个很窄的脉冲，或者频率快速扫过的 LFM 信号），它的"特征"很明显，稍微时间错开一点，波形就对不上了------就能分辨得很细。

而信号"变化有多快"，在频域里就体现为带宽 B 越大 。所以：带宽越大 → 时间分辨力越高 → 距离分辨率越好（ΔR 越小）。

雷达波走的是"来回"路径。如果目标距离是 \(R\)，那么电磁波走过的总路程是 \(2R\)，所需时间（时延）为：

\[\tau=\frac{2R}{c}\ =>\ R=\frac{c\tau}{2} \]

所以，距离差\(\Delta R\)对应时间差\(\Delta \tau\)

\[\Delta R = \frac{c}{2} \Delta \tau \]

因此要提高距离分辨率（降低\(\Delta R\)），就要能分辨很小的\(\Delta \tau\)

有个信号处理的基本原理（来自傅里叶变换的不确定性原理）,一个信号在时域的"最小可分辨时间间隔"大约是其频域带宽的倒数：

\[\Delta \tau \approx \frac{1}{B} \]

综合可得

\[\Delta R = \frac{c}{2B} \]

误区 正确理解
"载频越高，分辨率越好" ❌ 分辨率只看带宽 B ，不是载频 f**c。你可以用 1 GHz 载频 + 10 MHz 带宽，也可以用 10 GHz 载频 + 10 MHz 带宽，分辨率一样！
"脉冲越窄，分辨率越好" ✅ 对于简单脉冲雷达 是对的，因为窄脉冲天然带宽大（B ≈1/脉宽）。但脉冲压缩技术让我们可以用宽脉冲+大带宽达到同样效果，还能提高能量。

六、关于中心频率的定义

情况一 ：LFM 以载频 \(f_c\)为中心（对称调频）

  • 起始频率：\(f_{start}=f_c−\frac{B}{2}\)
  • 终止频率：\(f_{end}=f_c+\frac{B}{2}\)
  • 带宽：\(B=f_{end}−f_{start}=10MHz\)
  • 最高频率 \(f_0 + B\)。

这种定义在理论分析、匹配滤波设计中很常见。

情况二：LFM 从某个起始频率开始单向扫描（更贴近工程实际）

很多雷达系统并不强制让 LFM 以 \(f_c\)为中心，而是这样定义：

  • 起始频率：\(f_0\)

  • 终止频率：\(f_0 + B\)

  • 带宽：\(B=10MHz\)

  • 此时，中心频率（也叫"射频载频"）通常定义为：

    \[f_c=f_0 + \frac{B}{2} \]

所以最高频率 \(f_0 + B\)。

七、MATLAB 脉压仿真

matlab 复制代码 
%% LFM 脉冲压缩仿真（含 SLL 和 SNR 分析）
clear; close all; clc;

%% 系统参数
c = 3e8;               % 光速 (m/s)
fc = 1e9;              % 载频 1 GHz（仅用于显示，基带仿真可忽略）
B = 10e6;              % 带宽 10 MHz
T = 10e-6;             % 脉宽 10 微秒
fs = 50e6;             % 采样率（需 > 2*B，这里取 50 MHz）
ts = 1/fs;
N = round(T * fs);     % 采样点数
t = (-N/2 : N/2 - 1)' * ts;  % 时间向量（对称）


%% 1. 生成基带 LFM 信号（复数形式）
K = B / T;                      % 调频率
s = exp(1j * pi * K * t.^2);    % 基带 LFM
s(t < -T/2 | t > T/2) = 0;      % 加矩形窗（实际已由 t 范围限制）


%% 2. 频域分析
S = fftshift(fft(s));           % fft 计算出的结果直流和低频在两端，高频在中间。
                                % fftshif 的作用是使得直流和低频在中心，高频在两端。
f = (-N/2 : N/2-1)' * fs / N;   % 频率轴（基带）


%% 3. 脉冲压缩：匹配滤波
% 匹配滤波器 = s 的时间反转共轭
h = conj(flipud(s));            % flipud 的作用是上下翻转数组
y = conv(s, h, 'same');         % 脉压输出（无噪声）
                                % 卷积操作的输出 y 的长度必须与输入信号 s 的长度相同。
y = y / max(abs(y));            % 归一化主瓣为 1

% 添加白噪声（用于 SNR 计算）
SNR_in_dB = 10;                                 % 输入信噪比（dB）
noise_power = var(s) / (10^(SNR_in_dB/10));     % 根据输入 SNR 设置噪声功率
n = sqrt(noise_power/2) * (randn(size(s)) + 1j*randn(size(s)));
y_noisy = conv(s + n, h, 'same');
y_noisy = y_noisy / max(abs(y));                % 仍用无噪主瓣归一化（便于比较）


%% 4. 计算 SLL（旁瓣抑制比）
mag_y = abs(y);
[~, main_idx] = max(mag_y);                     % 主瓣位置，~为忽略输出变量值

% 排除主瓣附近区域（比如 ±2 个主瓣宽度），找最大旁瓣
mainlobe_width_samples = round(1/(B*ts));       % 理论主瓣宽度 ≈ 1/B
                                                % 1/B 是时间宽度（秒）,ts 是采样间隔（秒/点），这个式子是求主瓣占多少个采样点
                                                % 加round是因为数组的下标必须是整数

mask = true(size(mag_y));                       % size 返回数组的维度，比如 500 行 1 列: [500 1]
                                                % true 用于创建一个逻辑数组，维度与 size
                                                % 返回的完全相同，默认值都为true
mask(max(1, main_idx - mainlobe_width_samples) : min(end, main_idx + mainlobe_width_samples)) = false;
                                                % 把主瓣附近区域设为 false，表示"这些不是旁瓣，不能参与最大旁瓣搜索"
                                                % 上面两行的结果：mask 是一个逻辑数组，主瓣区域为 false，其余为 true
max_sidelobe = max(mag_y(mask));                % 只取出 mask 为 true 的那些点（即旁瓣区域的幅度值）找最大值

% SLL（dB）= 20log10(最大旁瓣幅度 / 主瓣幅度) = 20log10(最大旁瓣幅度)（因为主瓣=1）
SLL_dB = 20 * log10(max_sidelobe);              % 因为主瓣已归一化为 1

%% 5. Peak SNR（在有噪输出中计算）计算方法：主瓣峰值处的信号功率 / 噪声功率
peak_signal_power = abs(y_noisy(main_idx))^2;   % 峰值处信号功率
% 噪声功率估计：用远离主瓣的区域
noise_region = mag_y < 0.1;                     % 假找出所有幅度小于 0.1 的位置
                                                % 为什么选 0.1？
                                                % 主瓣归一化为 1，LFM 的第一旁瓣约 0.22（-13 dB），更远的旁瓣迅速衰减
                                                % 所以 远离主瓣的区域（如 |t| > 3/B）幅度通常 << 0.1
                                                % 这些区域几乎没有信号能量，只有噪声
if any(noise_region)                            % any 判断一个数组中是否存在任何非零元素
    noise_power_est = mean(abs(y_noisy(noise_region)).^2);
                                                % 用于得到噪声功率估计值
else
    noise_power_est = var(y_noisy - y);         % var() 计算方差：对零均值噪声，方差 = 功率
end
Peak_SNR_dB = 10 * log10(peak_signal_power / noise_power_est);

%% 6. 绘图
figure('Position', [100, 100, 1200, 900]);

% (a) 时域
subplot(3,1,1);
plot(t*1e6, real(s), 'b');
xlabel('时间 (\mus)'); ylabel('幅度');
title('LFM 信号（时域，实部）');
grid on;

% (b) 频域
subplot(3,1,2);
plot(f/1e6, abs(S), 'r');
xlabel('频率 (MHz)'); ylabel('|S(f)|');
title('LFM 信号频谱（基带）');
xlim([-B/2/1e6-1, B/2/1e6+1]);
grid on;

% (c) 脉冲压缩输出
subplot(3,1,3);
time_axis = (-length(y)/2 : length(y)/2 - 1)' * ts;
plot(time_axis*1e6, abs(y_noisy), 'k', 'LineWidth', 1.2);
hold on;
plot(time_axis(main_idx)*1e6, abs(y_noisy(main_idx)), 'ro', 'MarkerSize',8, 'MarkerFaceColor','r');
% 标出最大旁瓣
[~, sid_idx] = max(mag_y .* mask); 	% 在旁瓣区域找最大值
plot(time_axis(sid_idx)*1e6, abs(y_noisy(sid_idx)), 'bo', 'MarkerSize',6, 'MarkerFaceColor','b');

xlabel('时间 (\mus)'); ylabel('归一化幅度');
title(sprintf('脉冲压缩输出 | SLL = %.1f dB | Peak SNR = %.1f dB', SLL_dB, Peak_SNR_dB));
legend('脉压输出','主瓣峰值','最大旁瓣','Location','best');
grid on;
xlim([-3/B*1e6, 3/B*1e6]);  		% 显示约 ±3 个主瓣宽度

上面程序的执行结果如下：

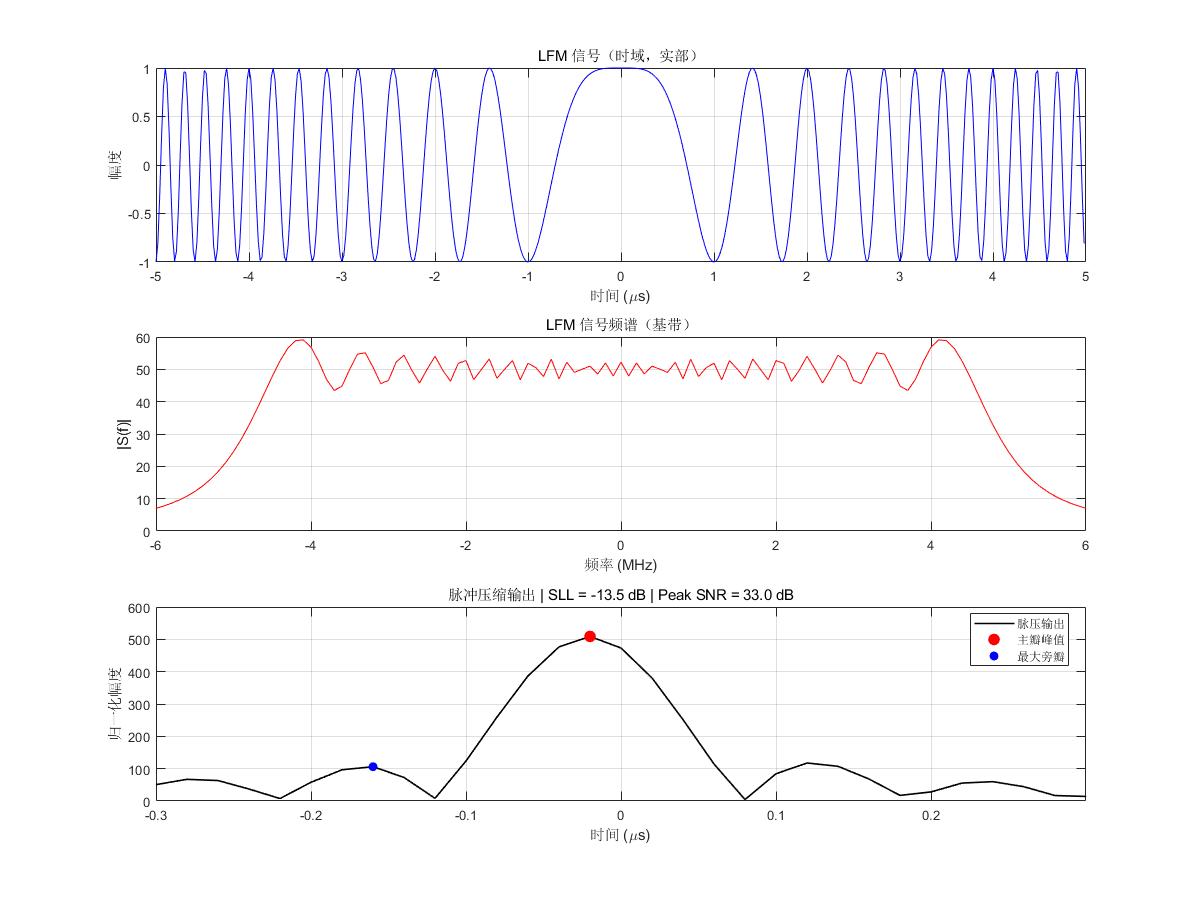
八、指标

8.1 旁瓣抑制比

什么是旁瓣抑制比，第七节仿真图图3展示了对 LFM 信号的脉冲压缩结果，很明显是由主瓣和若干个较小的旁边组成的，想象一下，如果旁瓣的幅度与主瓣相比并没有小很多的话，雷达会不会认为它是另一个回波脉压的主瓣了，这就可能会造成雷达的虚警。旁瓣抑制比就是反应旁瓣相对于主瓣幅度大小的指标。

计算方法如下：

  • 主瓣峰值幅度：记为 \(A_{main}\)
  • 所有旁瓣中最大的那个幅度：记为 \(A_{max\_sidelobe}\)
  • 旁瓣抑制比：\(SLL(dB)=20log_{10} \left( \frac{A_{max\sidelobe}}{A{main}} \right)\)

SLL 不加窗的典型值：13.2dB。这是因为压缩后的波形近似\(sinc(x)=\frac{sin(\pi x)}{\pi x}\)，其第一旁瓣就是 -13.2 dB。

这意味着：最强的旁瓣有主瓣约 22% 的高度。

使用加窗的方法能够改善 LFM 的 SLL。例如：Hamming 窗可将 SLL 降到 -41 dB，代价是主瓣变宽（距离分辨率下降）、峰值 SNR 降低。这里不展开。

8.2 峰值信噪比

在脉冲压缩输出的主瓣峰值时刻，信号功率与噪声功率之比：

\[Peak\ SNR = \frac{脉压后信号峰值功率}{输出噪声功率} \]

SLL 与 Peak SNR 的权衡关系：

方法 SLL（旁瓣） Peak SNR 主瓣宽度（分辨率）
理想 LFM（无窗） -13.2 dB（差） 最大（最优） 最窄（最优）
加 Hamming 窗 ≈ -41 dB（好） ↓ 损失 ~1.8 dB ↑ 变宽 ~1.8 倍
加 Taylor 窗（-30 dB） -30 dB（较好） ↓ 损失 ~0.8 dB ↑ 略微变宽

SLL 决定你"看不看得清真假目标"，Peak SNR 决定你"能不能从噪声里看到真目标"------LFM 脉冲压缩要在两者之间找平衡。

九、坐标问题

9.1 时域坐标有负值的解释

观察第七节图1，发现 LFM 信号的时域图的时间轴有负值，这是为什么？

在雷达信号处理（尤其是脉冲压缩）的仿真中，时间轴出现负值，并不是因为时间真的倒流了，而是出于 信号对齐、数学对称性和便于分析 的考虑。核心原因在于让信号"以零时刻为中心"。

在理论分析和仿真中，我们常常希望：

  • LFM 脉冲对称地分布在 t = 0 附近
  • 匹配滤波后的主瓣峰值正好出现在 t = 0

这样做的好处是：

  1. 数学表达简洁 （比如 LFM 相位写成 \(\pi Kt^2\)）
  2. 频谱是实偶函数或纯相位，便于理解
  3. 脉压输出的主瓣自然落在时间原点，不用额外计算延迟

举个例子，假设你有一个 10 微秒的 LFM 脉冲。如果从 t = 0 开始

matlab 复制代码 
t = 0 : ts : T-ts;   % [0, T)
  • 匹配滤波后，主瓣峰值会出现在 t ≈ T = 10 μs 处（因为卷积延迟）
  • 你想看"目标回波对齐时刻"，还得手动找峰值位置

如果以 t = 0 为中心（含负时间）：

matlab 复制代码 
t = (-T/2 : ts : T/2 - ts);   % [-5μs, +5μs)
  • 信号关于 0 对称
  • 匹配滤波器也对称设计
  • 输出主瓣自动出现在 t = 0
  • 旁瓣左右对称，SLL 计算更直观

9.2 从匹配滤波角度看

匹配滤波器的冲激响应是：

\[h(t)=s^∗(−t) \]

  • 如果原始信号 s(t) 定义在 [−T/2, T/2]，
  • 那么 h(t) 也在 [−T/2,T/2]
  • 两者卷积后，最大输出（相关峰）自然出现在 t = 0

这称为 零相位对齐（zero-phase alignment），是信号处理中的标准做法。

9.3 在真实雷达系统里

  • 发射信号确实从 t = 0 开始（没有负时间）
  • 接收回波有延迟 τ=2R/c
  • 匹配滤波输出的峰值出现在 t = τ

但在仿真或理论分析时，我们可以：

  • 假设目标就在"参考距离"上（比如 R=0 → τ=0）
  • 把信号中心对齐到 t=0，等效于已经补偿了传播延迟
热门推荐
01GitHub 镜像站点02【保姆级教程】免费使用Gemini3的5种方法！免翻墙/国内直连03BongoCat - 跨平台键盘猫动画工具04UV安装并设置国内源05安娜的档案(Anna’s Archive) 镜像网站/国内最新可访问入口（持续更新）06Linux下V2Ray安装配置指南07Google Antigravity：无法登录？早期错误、登录修复和用户反馈指南08Labelme从安装到标注：零基础完整指南09全球最强模型Grok4，国内已可免费使用！（附教程）1046个Nano-banana 精选提示词，持续更新中