什么是数字签名?
借用书里面给的一个例子,如果两个参与方,分别为 A l i c e Alice Alice与 B o b Bob Bob。 A l i c e Alice Alice想要让 B o b Bob Bob相信一条消息 m m m是她发送的。如何操作?
一种简单的方法是使用公钥加密。
- A l i c e Alice Alice首先生成一对公私钥 ( p k , s k ) (pk,sk) (pk,sk)并把公钥 p k pk pk公开给 B o b Bob Bob。
- A l i c e Alice Alice使用自己的私钥 s k sk sk对消息 m m m进行签名得到 σ m \sigma_m σm。
- B o b Bob Bob接收到 ( m , σ m ) (m,\sigma_m) (m,σm)之后,使用Alice的公钥 p k pk pk验证 σ m \sigma_m σm是否正确。
具体的构造方案,可以使用RSA,RSA的详细过程参考这一篇博客RSA加密。下面直接分析过程。
- A l i c e Alice Alice生成RSA公钥 n , d n,d n,d并公开给 B o b Bob Bob,保留私钥 e e e。
- A l i c e Alice Alice使用自己的私钥 e e e对消息 m m m进行签名得到 σ m = m e mod n \sigma_m=m^e\ \text{mod}\ n σm=me mod n。
- B o b Bob Bob接收到 ( m , σ m ) (m,\sigma_m) (m,σm)之后,使用Alice的公钥 n , d n,d n,d验证 ( σ m ) d mod n = m (\sigma_m)^d\ \text{mod}\ n=m (σm)d mod n=m。
正确性验证
( σ m ) d mod n = m d e mod n = m φ ( n ) k + 1 mod n = m φ ( n ) k ∗ m mod n = m (\sigma_m)^d\ \text{mod}\ n=m^{de}\ \text{mod}\ n=m^{\varphi (n)k+1}\text{mod}\ n=m^{\varphi (n)k}*m\ \text{mod}\ n=m (σm)d mod n=mde mod n=mφ(n)k+1mod n=mφ(n)k∗m mod n=m。
安全性验证
B o b Bob Bob始终不知道 A l i c e Alice Alice的私钥 e e e。所以签名方案是安全的。
形式化的签名方案(共有四个算法)
- 系统生成算法(SysGen):输入一个安全参数 λ \lambda λ,返回一个系统参数 S P SP SP。
- 密钥生成算法(KeyGen):输入系统参数 S P SP SP,返回公私钥对 ( p k , s k ) (pk,sk) (pk,sk)。
- 签名算法(sign):输入消息 m m m,私钥 s k sk sk和系统参数 S P SP SP。返回 m m m的签名 σ m \sigma_m σm。
- 验证算法(Verify):输入 ( m , σ m ) (m,\sigma_m) (m,σm),公钥 p k pk pk和系统参数 S P SP SP。如果 σ m \sigma_m σm是 m m m的有效签名返回 a c c e p t accept accept;否则 r e j e c t reject reject。
正确性 要求给定任何 ( p k , s k , m , σ m ) (pk,sk,m,\sigma_m) (pk,sk,m,σm),如果 σ m \sigma_m σm是 m m m的一个有效签名(使用私钥 s k sk sk),那么验证算法(Verify)将会返回 a c c e p t accept accept。
安全性 要求在没有私钥 s k sk sk的情况下,对于概率多项式敌手(PPT)想要伪造一个消息 m m m的签名 σ m \sigma_m σm来通过验证是很困难的。
如何证明一个签名方案是安全的?
基于游戏的证明方法
假设存在挑战者 C \mathcal C C与敌手 A \mathcal A A。二者的关系是挑战者生成一个签名方案,而敌手去试图打破这个签名方案。二者进行如下交互
- 挑战者 C \mathcal C C首先生成一对公私钥 ( p k , s k ) (pk,sk) (pk,sk),把公钥 p k pk pk发给敌手,私钥自己保留。
- A \mathcal A A可以对任意消息做签名的问询。
- A \mathcal A A返回一个未被问询过的新消息的伪造签名。
选择消息攻击下存在性不可伪造安全模型(EU-CMA:Existential unforgeability against chosen-message attacks)的描述如下
- 初始化:令 S P SP SP为系统参数。挑战者 C \mathcal C C运行密钥生成算法(KeyGen)得到公私钥对 ( p k , s k ) (pk,sk) (pk,sk),把公钥 p k pk pk发给敌手 A \mathcal A A,挑战者保留私钥 s k sk sk来回应敌手对消息的签名问询。
- 问询:敌手对任意选择消息做出问询。对于消息 m i m_i mi的签名问询, C \mathcal C C运行签名算法(sign)计算 σ m i \sigma_{m_i} σmi并返回给敌手。
- 伪造:如果敌手可以返回一个对消息 m ∗ m^* m∗的伪造签名 σ m ∗ \sigma_{m^*} σm∗( m ∗ m^* m∗在问询阶段没有被敌手问询过且 σ m ∗ \sigma_{m^*} σm∗是 m m m的一个有效签名),则敌手赢得游戏。
设敌手赢得游戏的概率为 ϵ \epsilon ϵ。交互流程图如下:
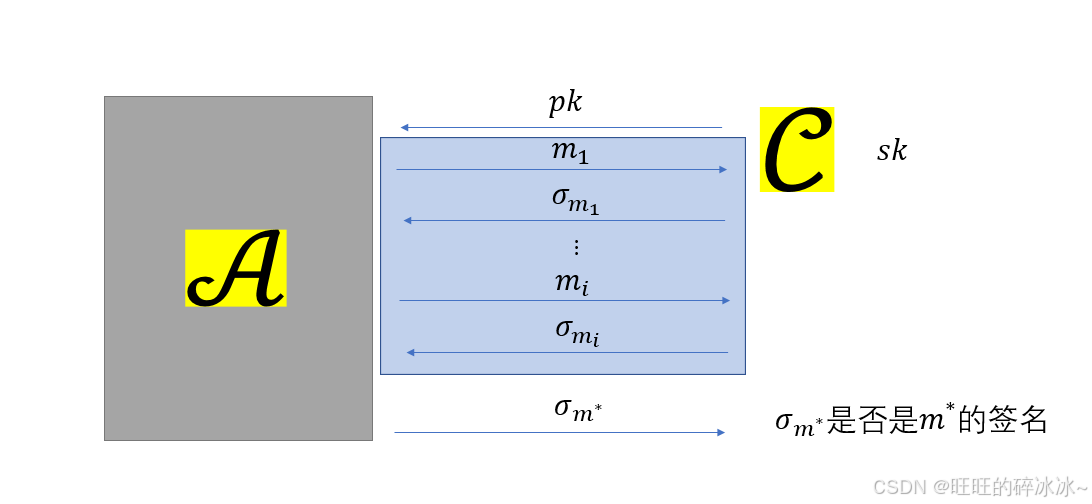
给一个定义。这里直接贴原文。

下面还有一个在选择消息攻击下强不可伪造安全(SU-CMA)的定义。

二者的主要区别在于(SU-CMA)放宽了对消息 m ∗ m^* m∗的 限制,只要敌手可以伪造
出一个有效的签名 σ m ∗ \sigma_{m^*} σm∗即可。 m ∗ m^* m∗可以是除了敌手问询过的任意消息。