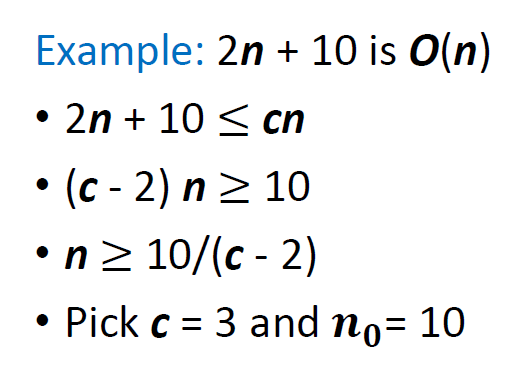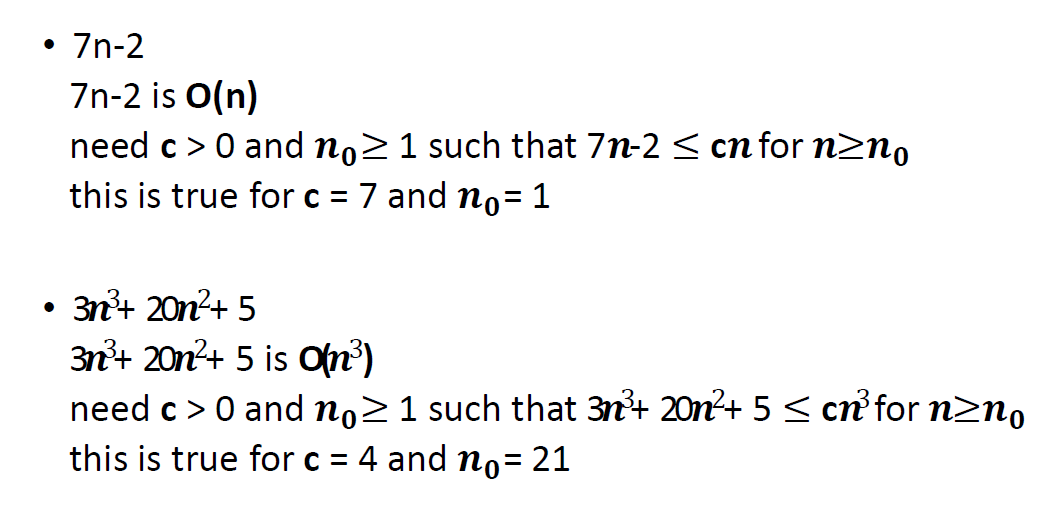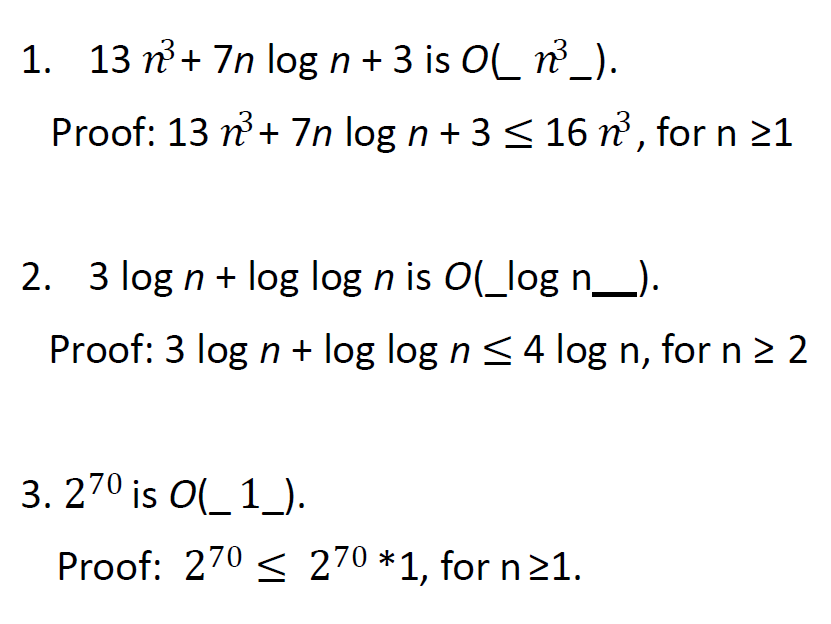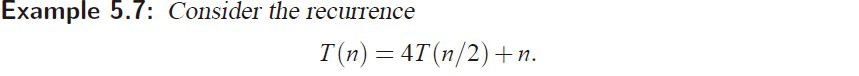算法复杂度


-
O(n) :表示算法的渐进上界。如果一个算法的运行时间是O(n),那么它的运行时间最多与输入规模n成正比。换句话说,当输入规模n增加时,算法的运行时间不会超过某个常数倍的n。比如,如果一个算法的时间复杂度是O(n),那么它的运行时间可能是3n,5n,100n等。
-
Ω(n) :表示算法的渐进下界。如果一个算法的运行时间是Ω(n),那么它的运行时间至少与输入规模n成正比。换句话说,当输入规模n增加时,算法的运行时间不会比某个常数倍的n小。比如,如果一个算法的时间复杂度是Ω(n),那么它的运行时间可能是n,2n,100n等。
-
Θ(n) :表示算法的紧密界限。如果一个算法的运行时间是Θ(n),那么它的运行时间与输入规模n成正比,并且上界和下界是相同的。换句话说,当输入规模n增加时,算法的运行时间将以线性方式增长。比如,如果一个算法的时间复杂度是Θ(n),那么它的运行时间可能是3n,n,100n等,但是不会超过某个常数倍的n。
单纯判断算式
e.g1
e.g2
e.g3
e.g4

C, 应该是O(n^2)

e.g5

A
一般的算法复杂度
e.g1
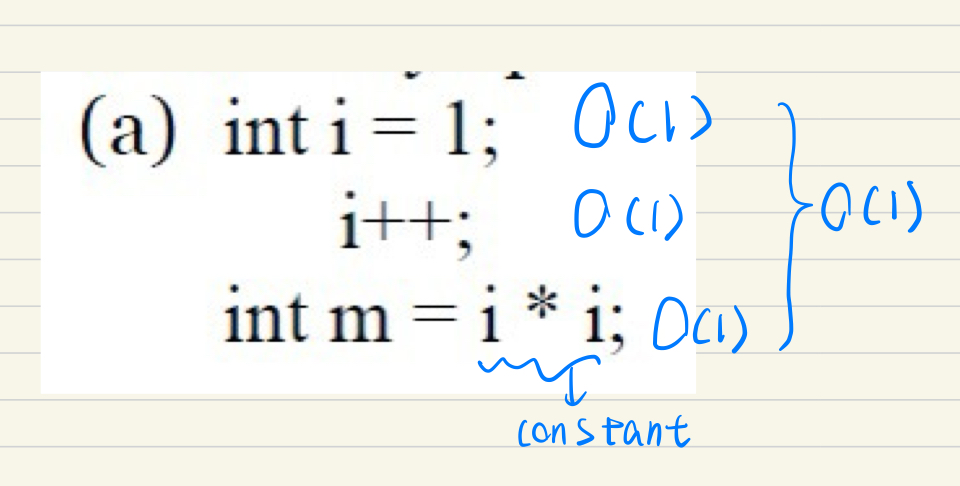

*

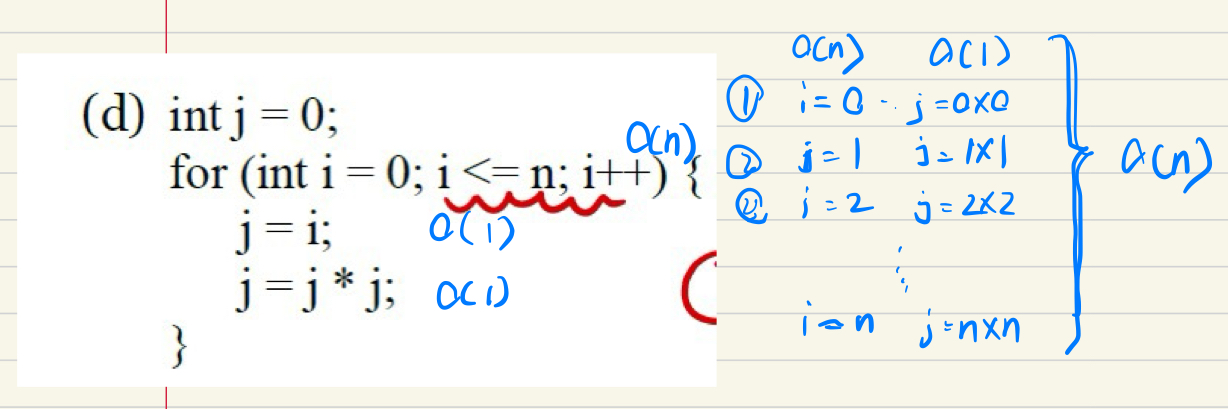

e.g2*

是这样的,用n^2进行遍历,然后n进行计算,乘起来就是n^3
e.g3


e.g4*

注意第二题,log(a)+log(b) = log(ab) 我反正忘了哈哈哈哈哈
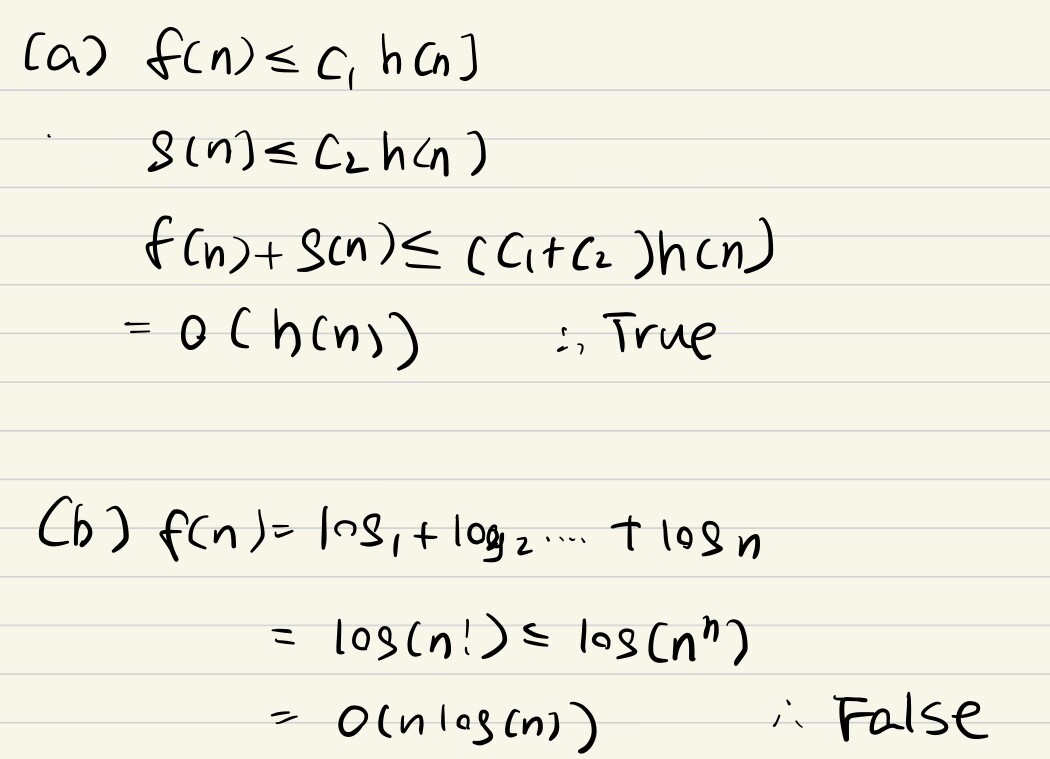
e.g5 summation表达*

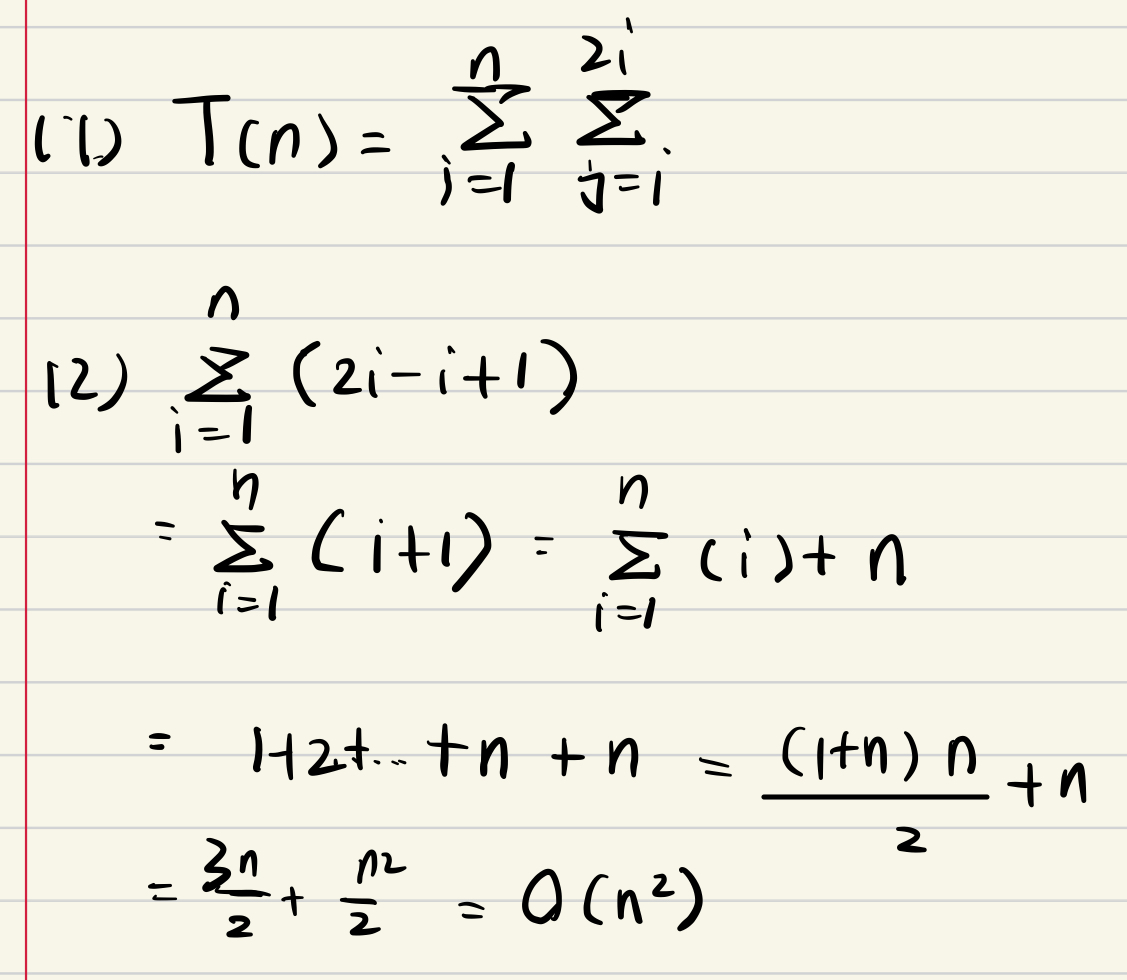
递归
e.g1*

后缀运算
主要考察的是栈
注意,减号的话是栈[-2]- 栈[-1]
e.g1
(1)
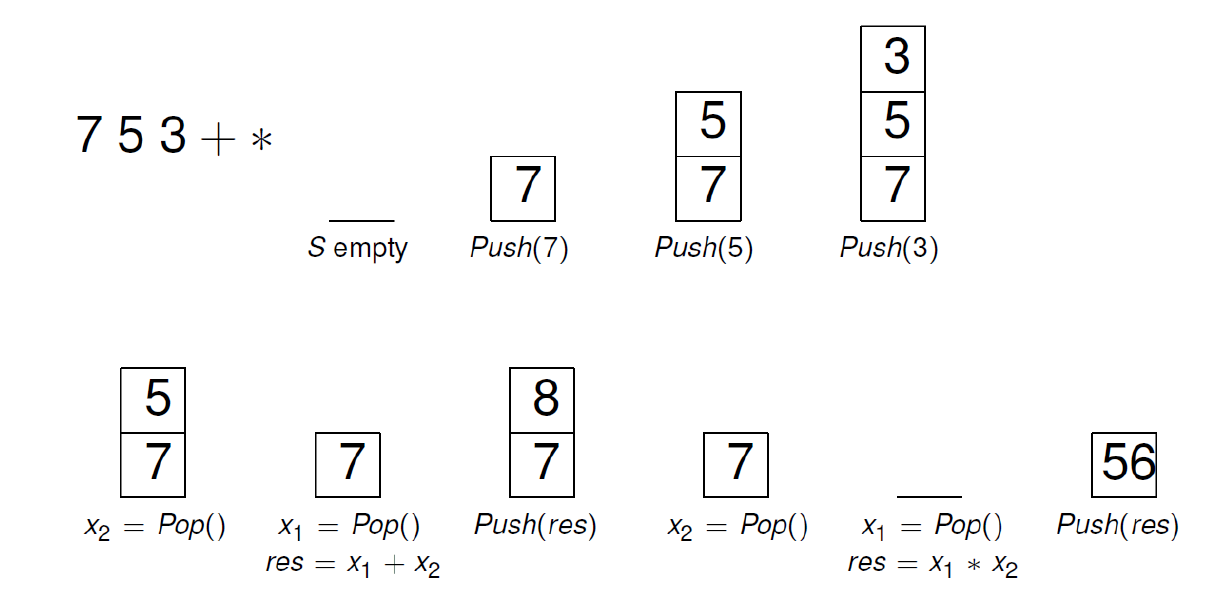
(2)

(3)
e.g2

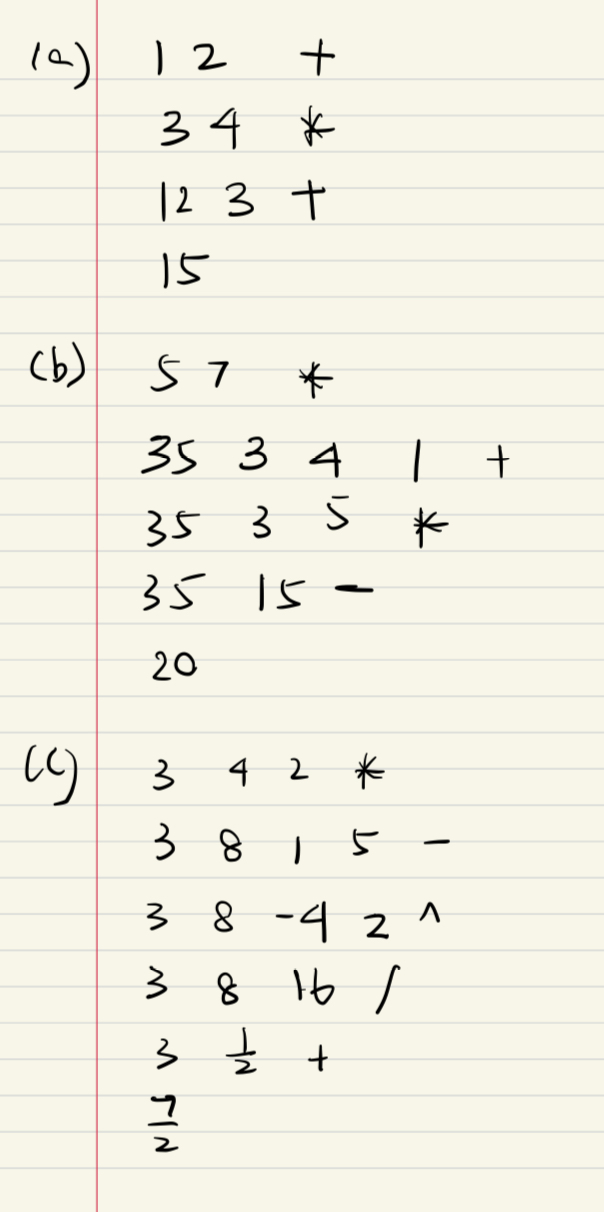
e.g3

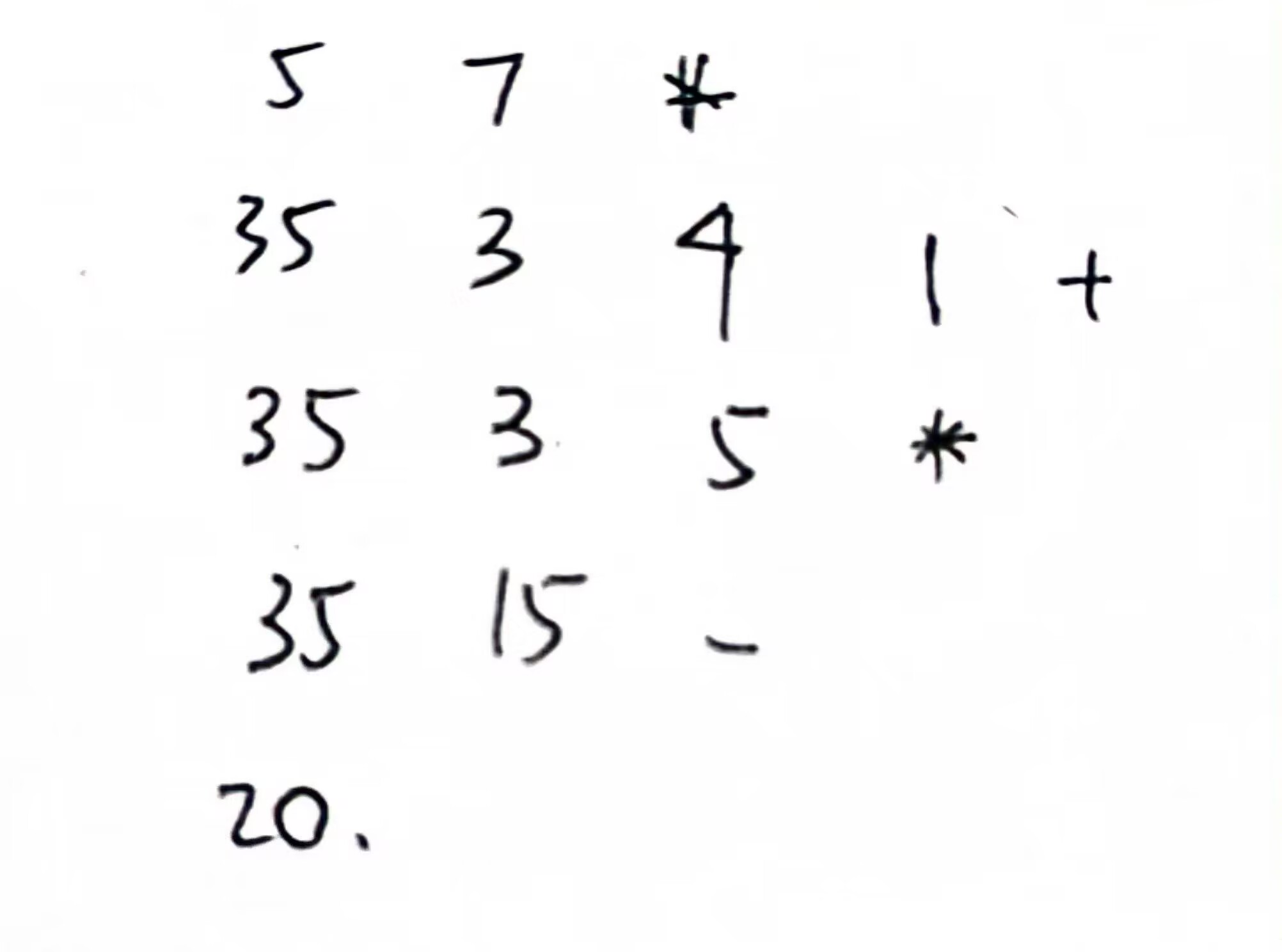
二叉树
一个好用的数据可视化网站Data Structure Visualization
节点深度 O(n)
树深度O(n)
查找O(n)(二分法)
遍历 O(n)
pre order 前序:中左右
in order中序:左中右
post order 后序:左右中
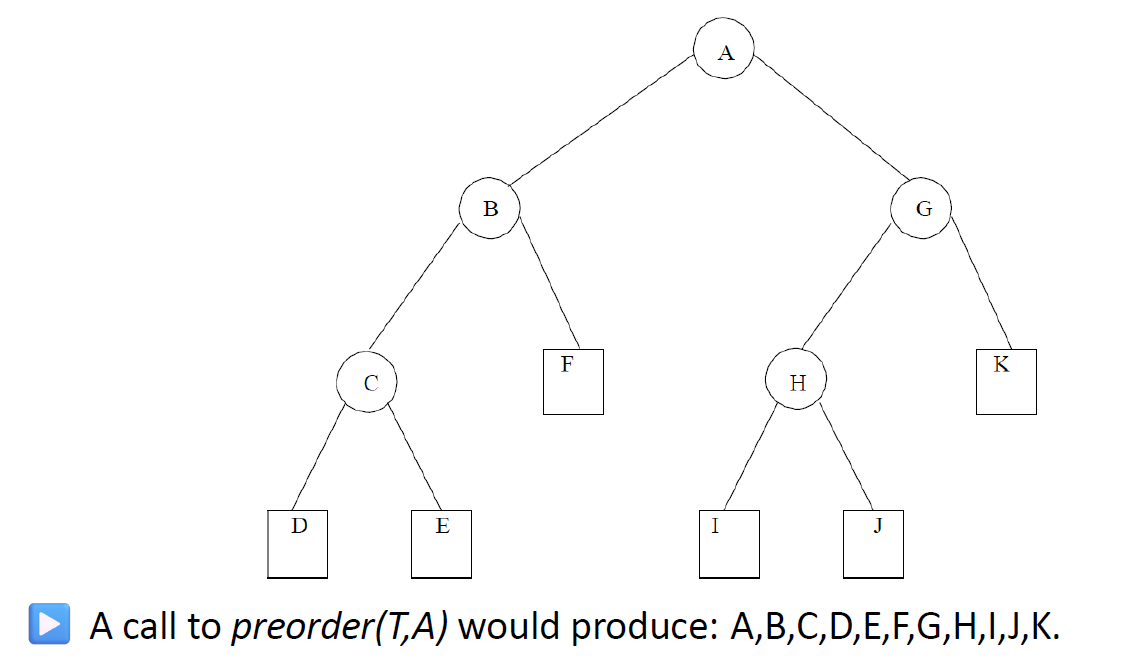

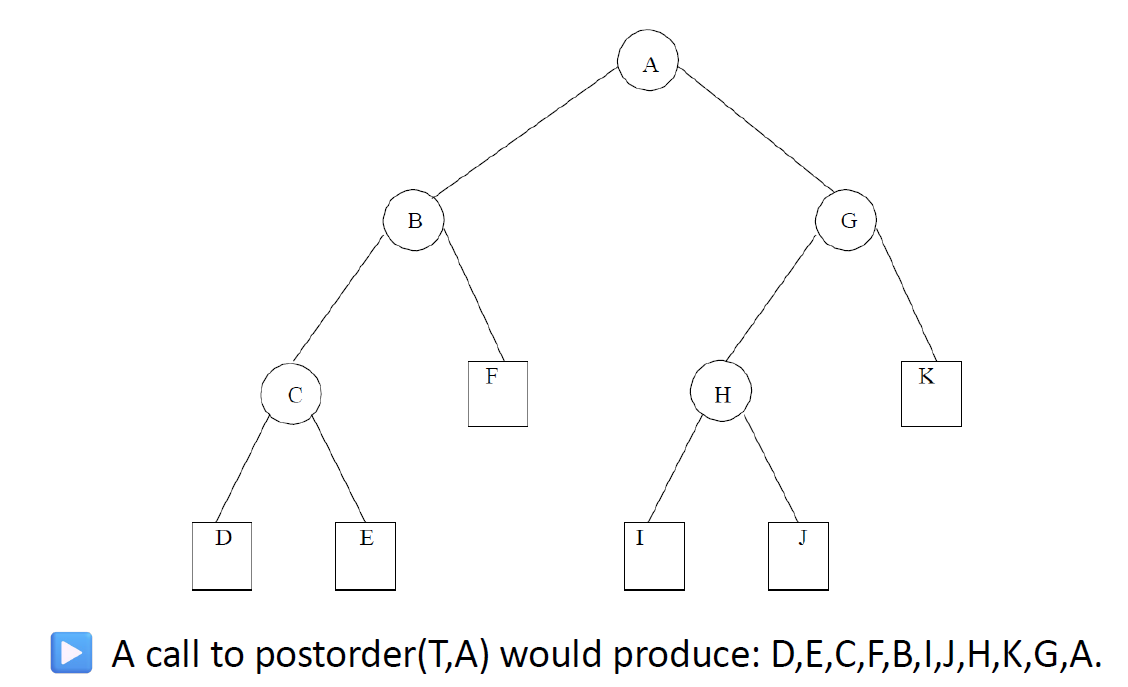
e.g1根据遍历绘制树


Binary search tree 二叉搜索树
二叉搜索树是一种特殊的二叉树,具有以下性质:
对于每个节点 NNN:
所有左子树节点的值都小于或等于节点 N的值
所有右子树节点的值都大于节点 N的值
查找 O(logn)-O(n)
e.g1 节点能构成多少个二叉树
用这个卡塔兰公式得
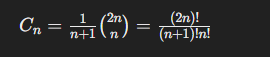

B
0/3 =5
1/2 =2
2/1 = 2
3/0 = 5
5+2+2+5=14
AVL tree 平衡二叉树
Height-Balance属性: 对于任何节点n, n的左右子树的高度最多相差1
All operations (search, insertion, and removal) on an AVL tree with n elements can be performed in O(log n)time
e.g1
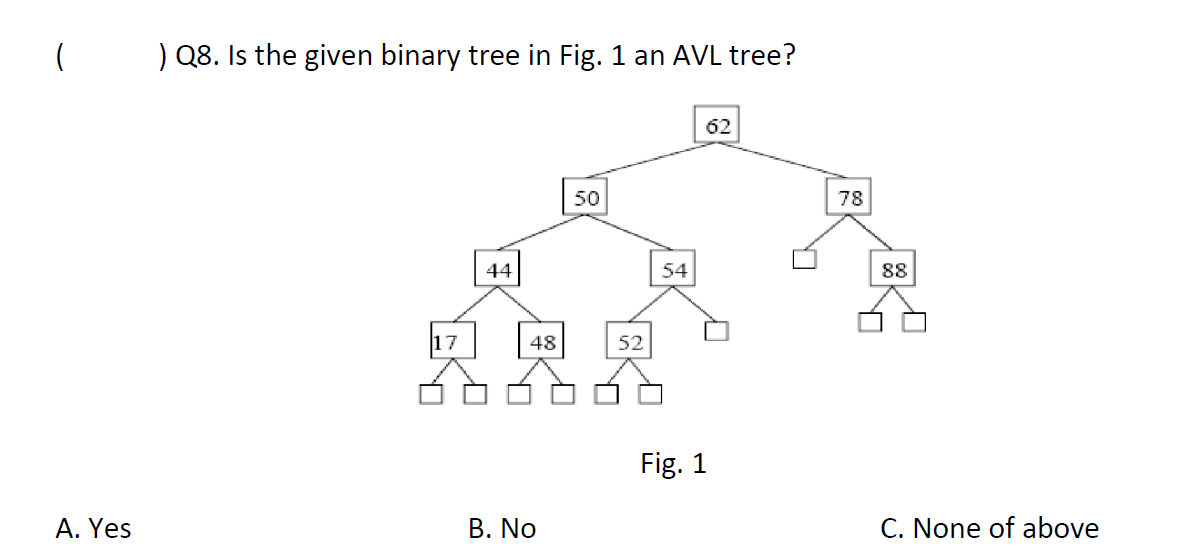
是的,左右节点响相差不超过1
添加节点O(log n)
是在树枝的叶节点添加,再转上去
集合进阶-11数据结构(平衡二叉树旋转机制)_哔哩哔哩_bilibili
右边多了左旋,左边多了右旋
简单情况:
以左旋为例:
1)以不平衡点节点作为支点
2)把支点左旋降级,变成左子节点,晋升原来右子节点
复杂情况:
1)以不平衡点作为支点
2)将根节点右侧往左拉
3)原先的右子节点变成新的父节点,并把多余的左子节点出让,给已经降级的根节点当右子节点
四种情况:
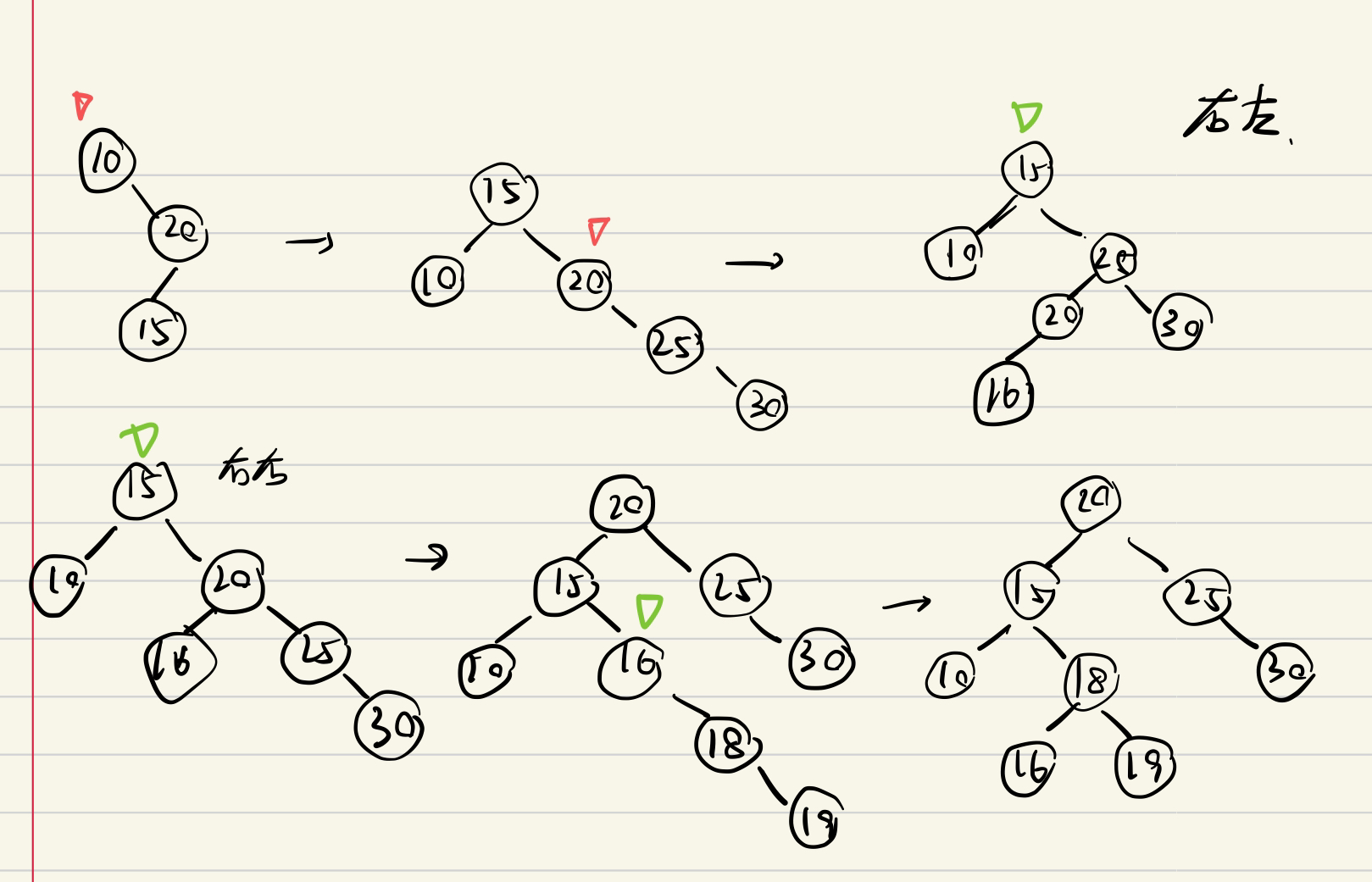
- 左-左(LL)失衡:右旋。
- 右-右(RR)失衡:左旋。
- 左-右(LR)失衡:先左旋后右旋。
- 右-左(RL)失衡:先右旋后左旋。
e.g1 插入节点
插入节点后检测平衡,删除节点后面的节点顶替后检查平衡
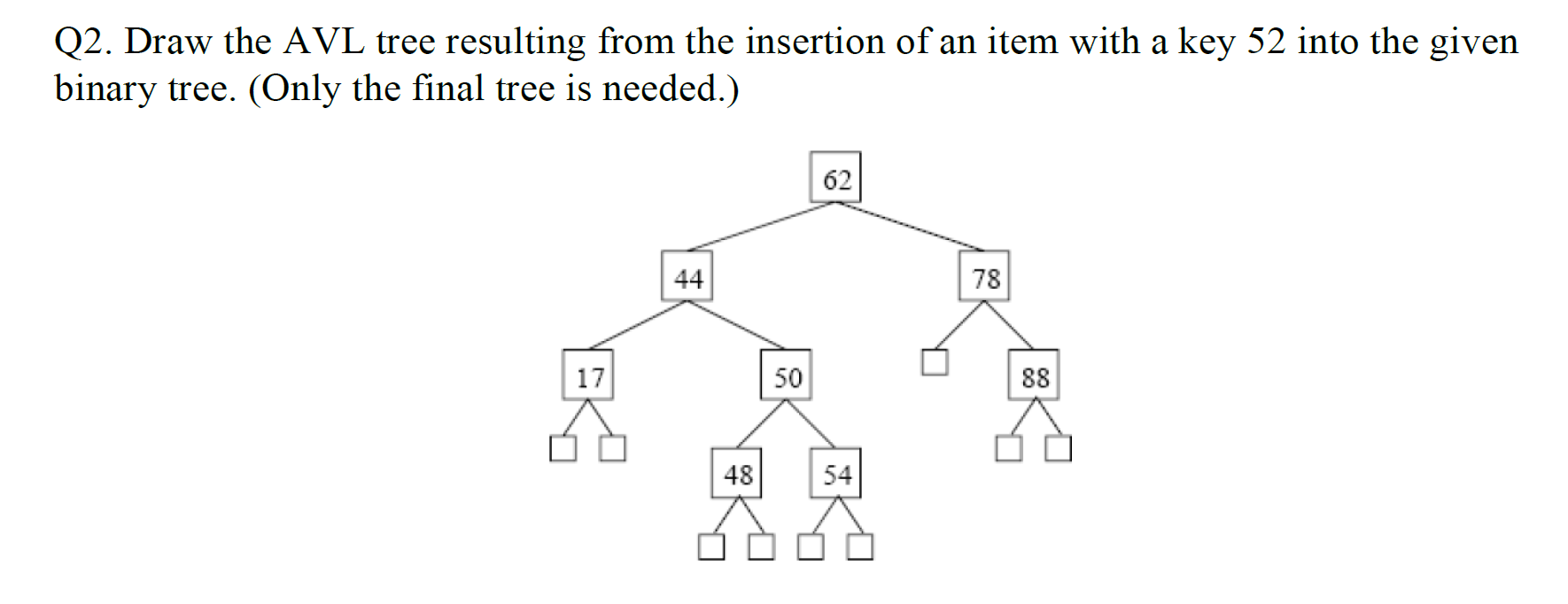
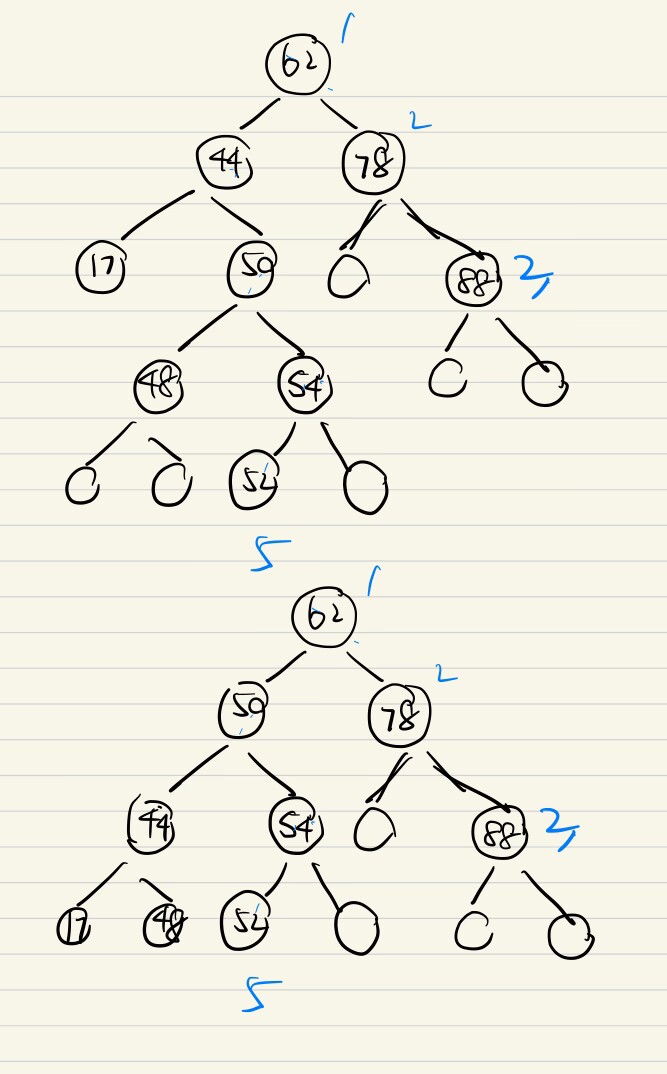
e.g3 构建AVL

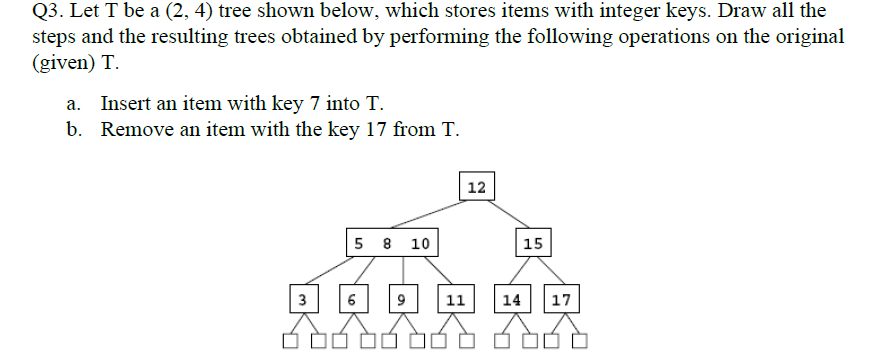
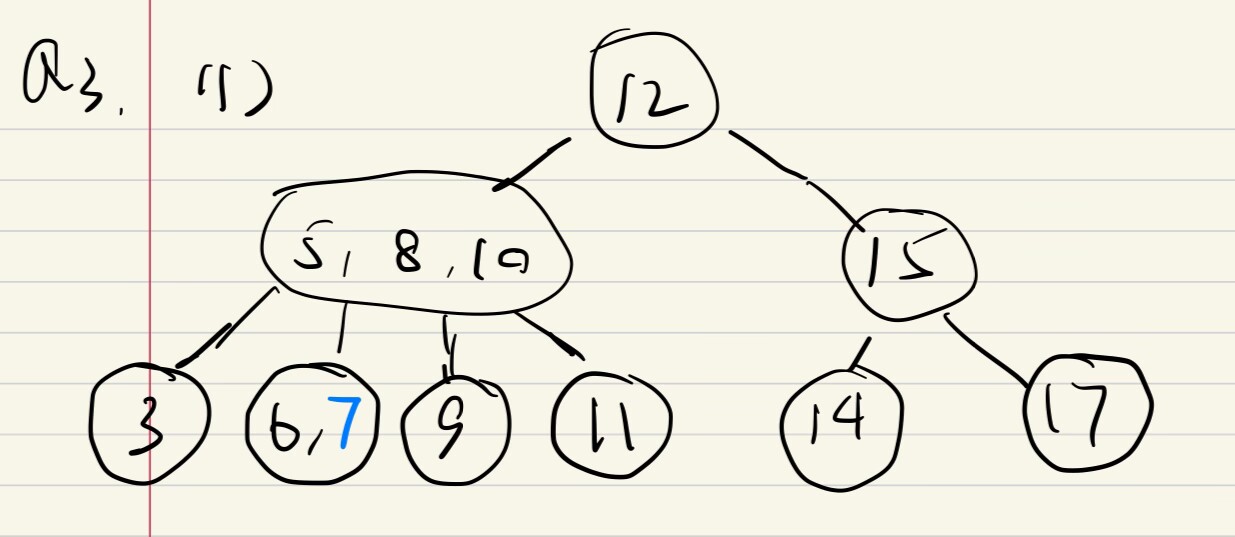
(2,4)树
has height O(logn)
查找 O(logn)
(2,4)树(也称为2-4树或2-3-4树)是一种多路搜索树,具有以下属性:
节点大小属性:每个内部节点最多有四个子节点
深度属性:所有外部节点具有相同的深度
根据子节点的数量,(2,4)树的内部节点被称为2节点、3节点或4节点
注意,相同的元素产生的(2,4)树可能会不一样,取决于节点插入的顺序
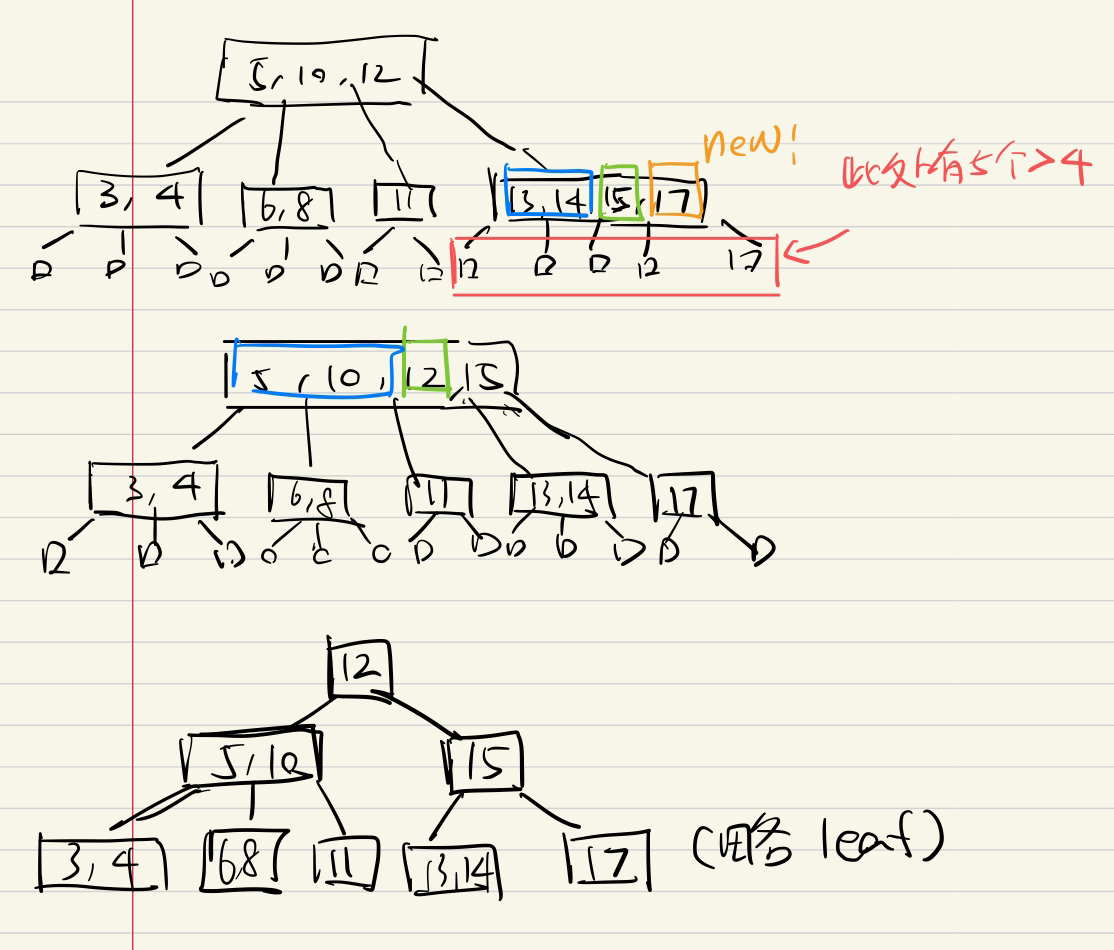
e.g1 树高O(logn)
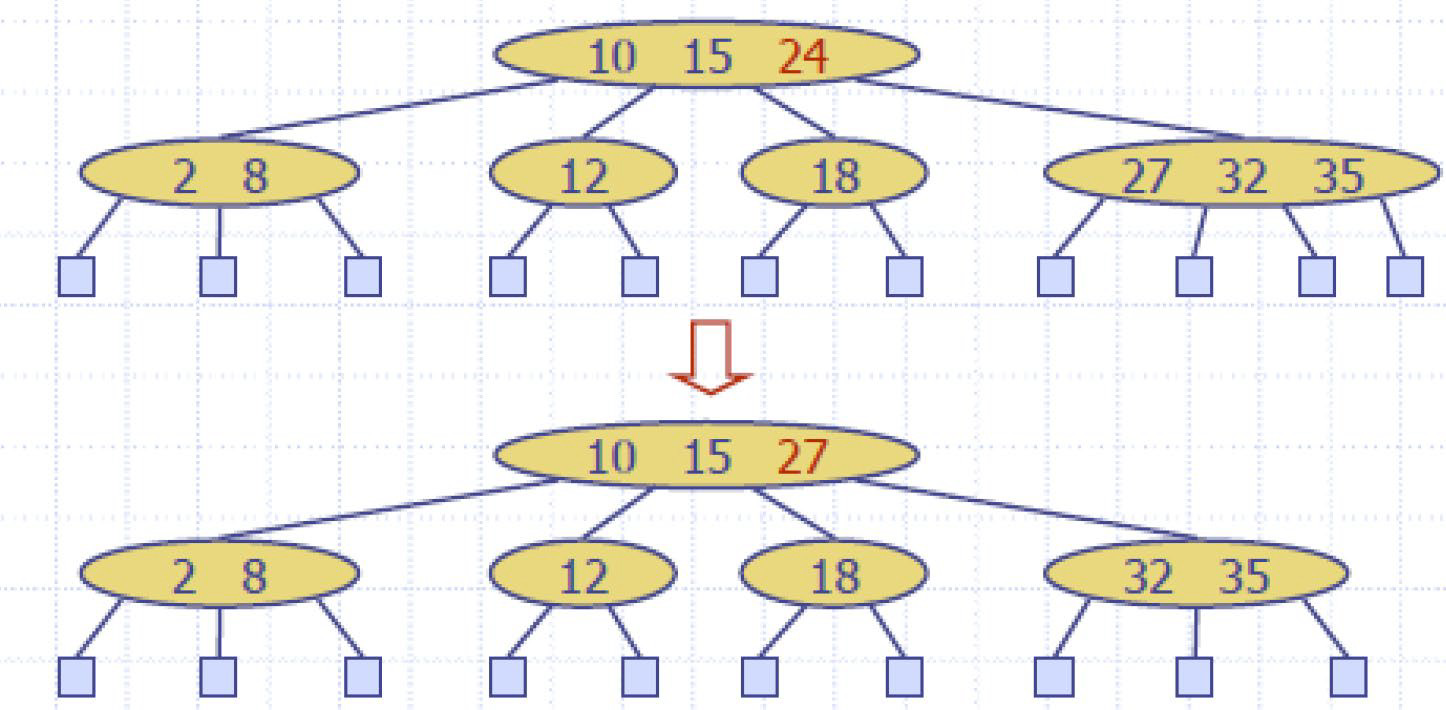
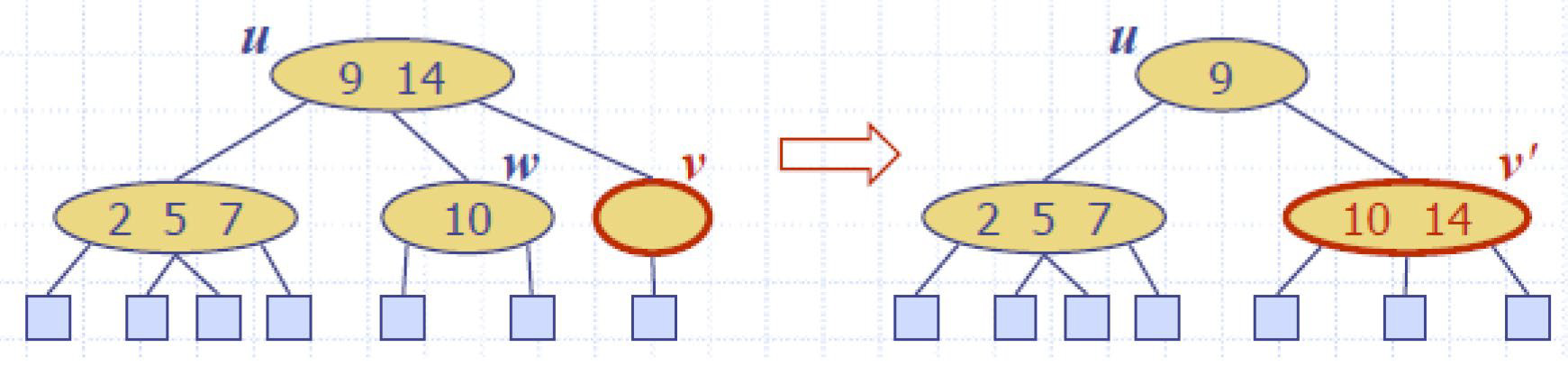
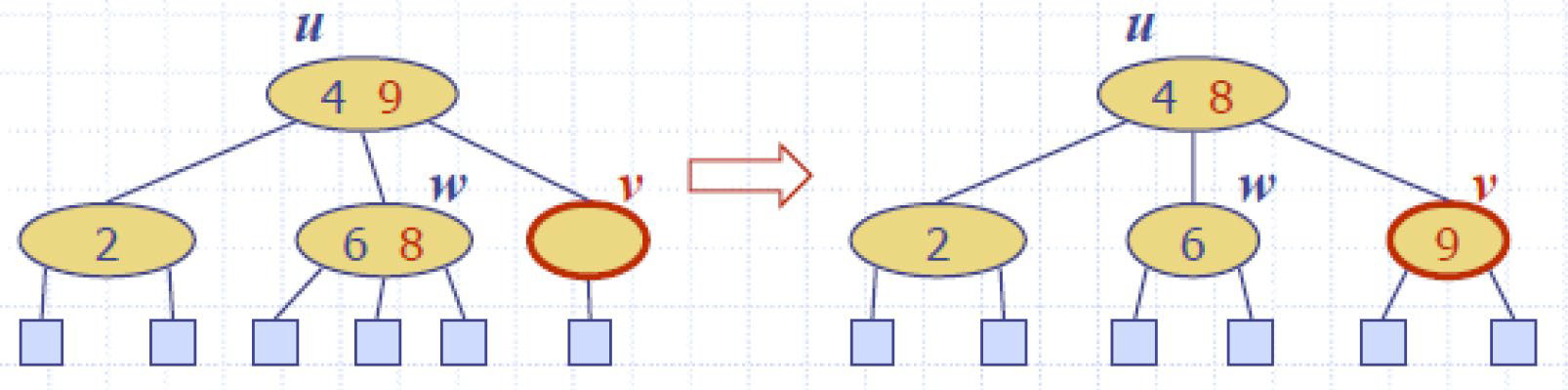
增O(logn)
e.g1
添加节点17
删O(logn)


e.g2增/删*
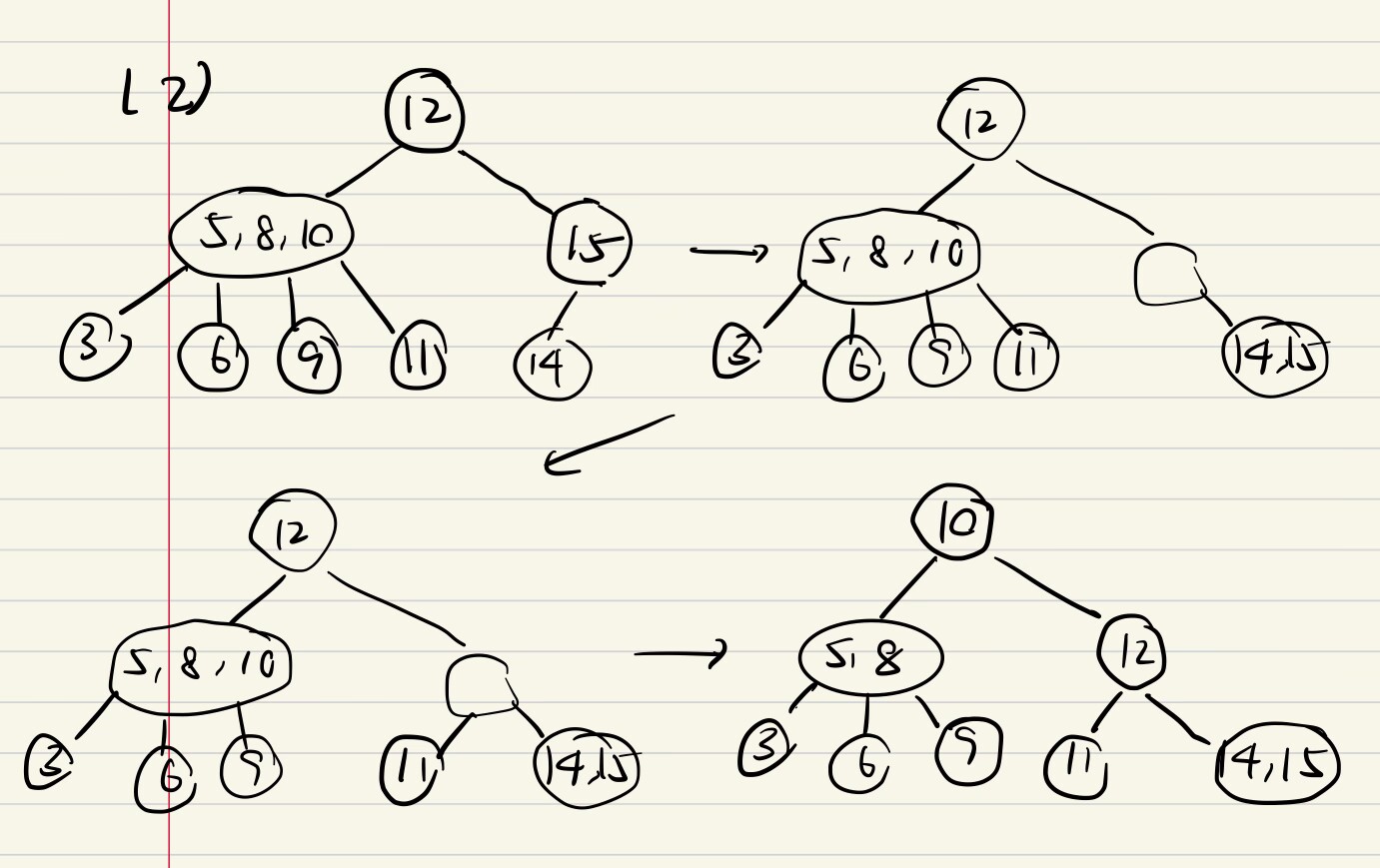
Heap 堆
【从堆的定义到优先队列、堆排序】 10分钟看懂必考的数据结构------堆_哔哩哔哩_bilibili
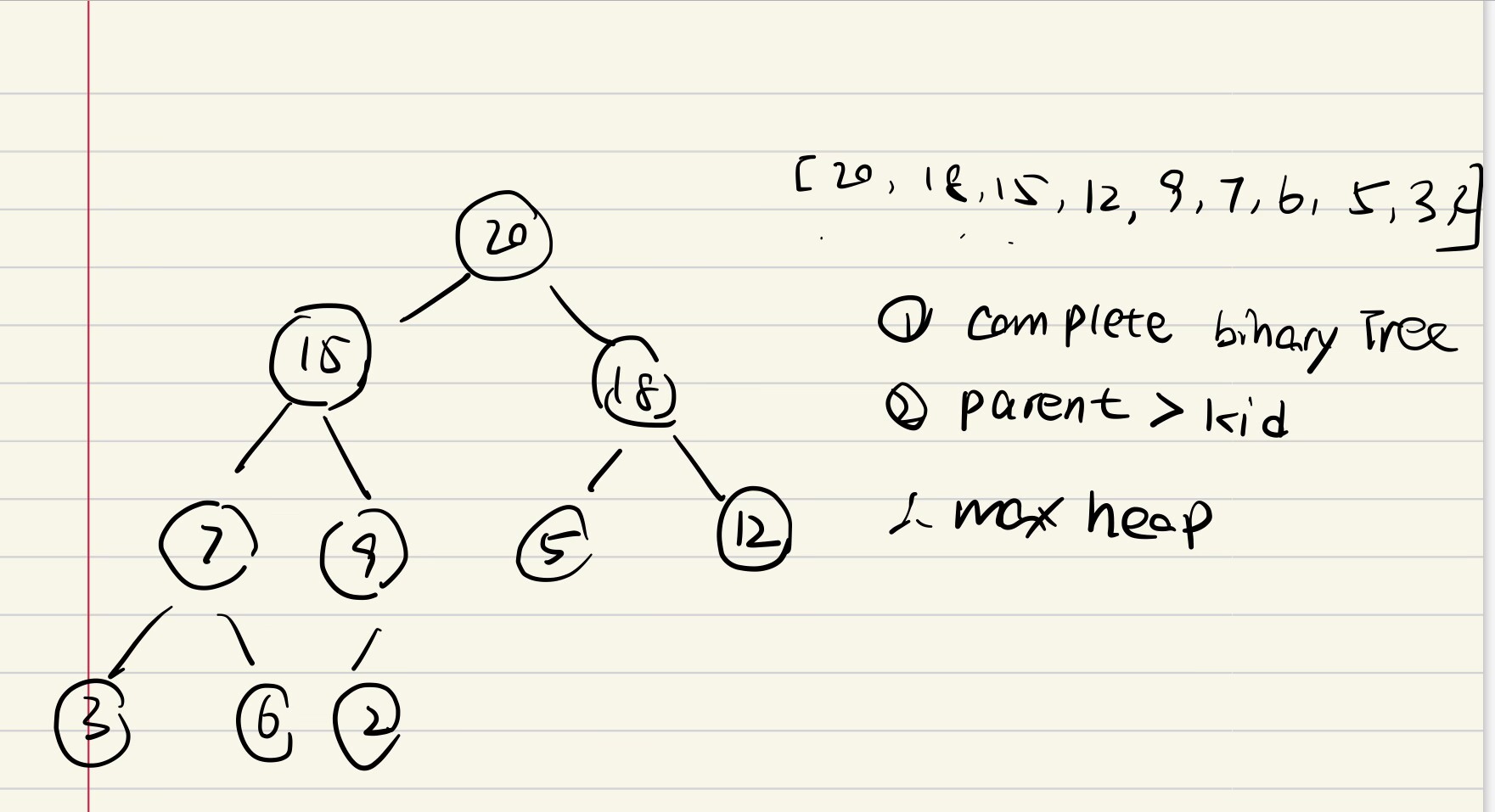
堆是一棵二叉树,在其内部节点上存储键,并满足以下属性:对于每个内部节点v,除了根节点key(v) ≥key(parent(v))
•节点中的键。
•父键不大于子键。
数组表示。
•索引从1开始。
•按等级顺序获取节点。
For any given node at position i:
• Its Left Child is at [2*i] if available.
• Its Right Child is at [2*i+1] if available.
• Its Parent Node is at [⌊i/2⌋] if available.
因此,堆可以用数组表示,因为堆的下标和内容是一一对应的
注意,同[2,4]树一样,同一组数可能形成不同的堆
完全二叉树?
没有左子树不能有右子树
上一层没有铺满,不能有下一层
优先队列
堆是优先级队列的一种实现,对于插入和删除都是有效的。
新的元素插入队列,弹出最小/最大元素O(logn)
可以进行排序,将队列的元素依次弹出
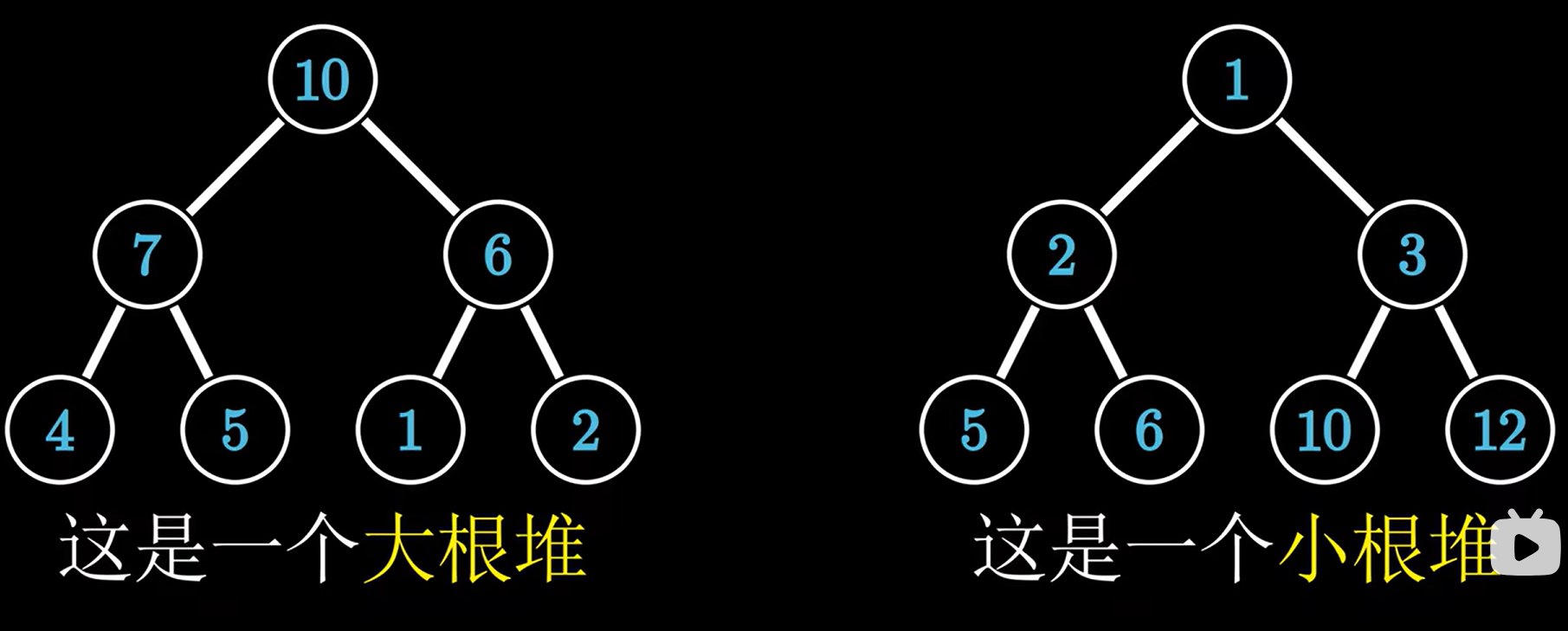
max heap 大根堆,min heap 小根堆

e.g1
.
e.g2

C
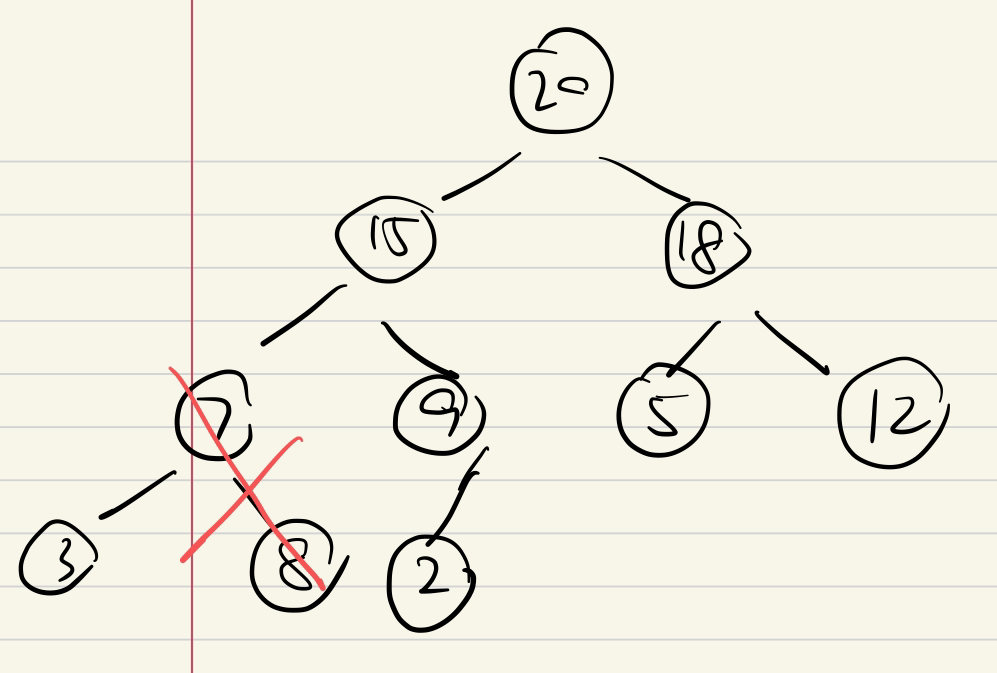
上/下滤 O(logn)
Up-heap bubbling 上滤
上滤用于插入新元素并维护堆的性质,将新元素逐级向上移动以确保其在正确的位置。
Down-heap bubbling 下滤
下滤用于删除堆顶元素或修改堆顶元素后,重新调整堆的结构,将堆顶元素逐级向下移动以确保其在正确的位置。
注意在堆中,通常对于节点的下沉操作是有方向性的。对于最大堆(Max Heap),节点的下沉操作是沿着较大的子节点方向进行的,类似地,对于最小堆(Min Heap),节点的下沉操作是沿着较小的子节点方向进行的。
建堆
1)从叶节点插--上滤O(nlogn)
- 先把数组中的数依次插入堆,然后再对每个父节点进行下率O(n)
(个人感觉考试的时候还是写上滤会清楚一些)
e.g1
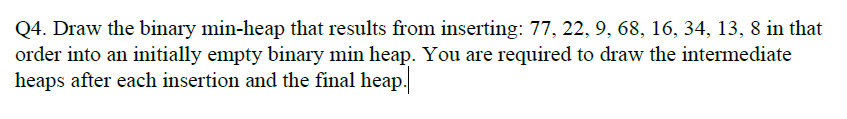
堆排序O(nlogn)
堆顶元素弹出后用最后一个元素堆叠到堆顶,然后下滤
大根堆下滤后变成小根堆,排序完是正序
小根堆下滤后变成大根堆,排序完是倒序
Lec8 分治法 Divide and conquer
将一个规模为n的问题u分解为k个规模为较小的子问题,子问题相互独立且与原问题相同,递归地求解这些子问题,然后利用子问题的解合并构造出原问题的解
设计:分解(Divide);递归求解(Conquer);合并(Combine)
分析:
1.建立递归方程T(n) = aT(n/b)+f(n)
2.求解递归方程T(n)
Sort
MergeSort

QuickSort

Master Method 主定理
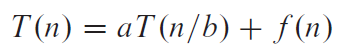

e.g1 case1
直接套公式
我写的
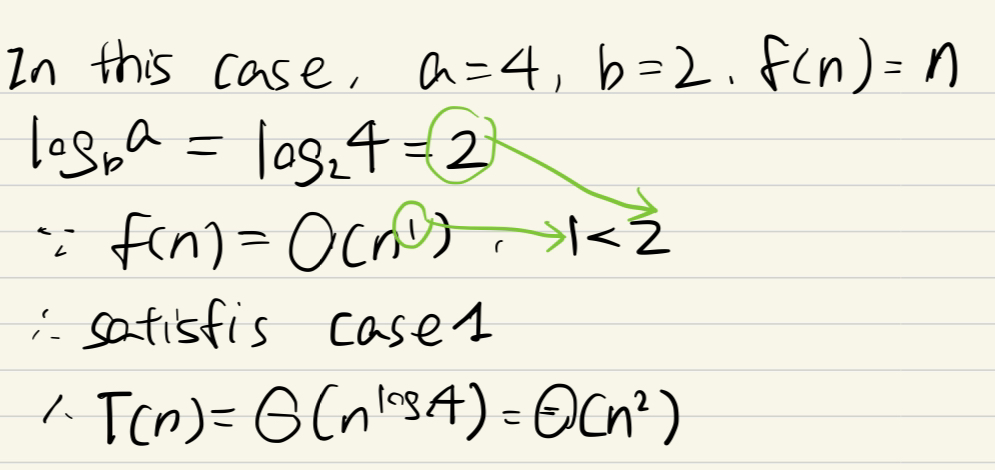
标答:
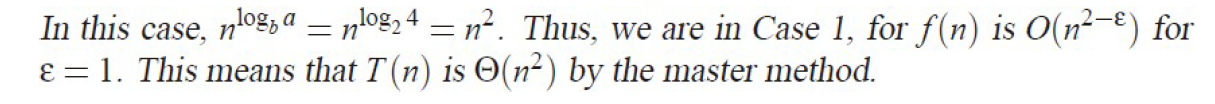
e.g2 case2
直接套公式

我写的
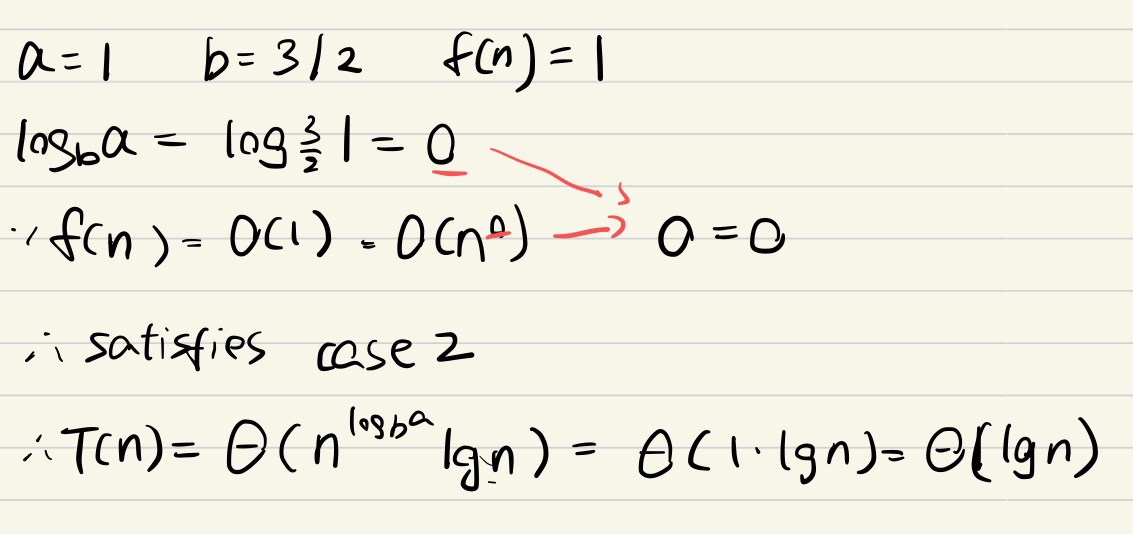
标答
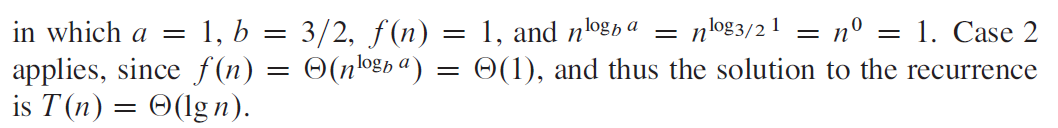
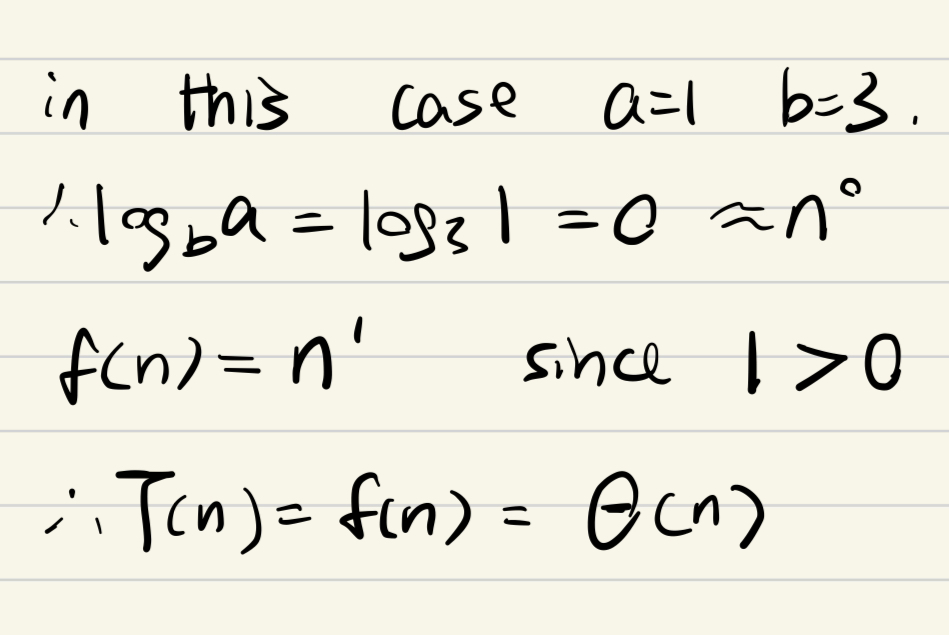
e.g3 case3
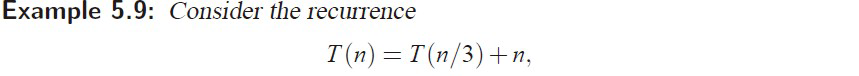
标答
e.g4 注意lgn有坑!*****

标答
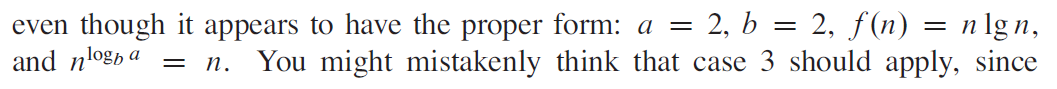
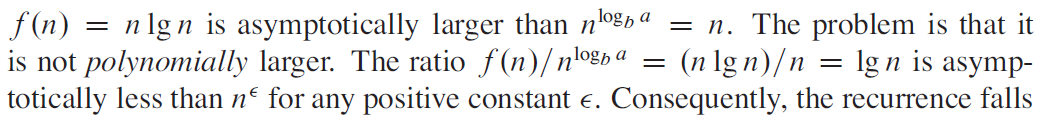
e.g5 同e.g4
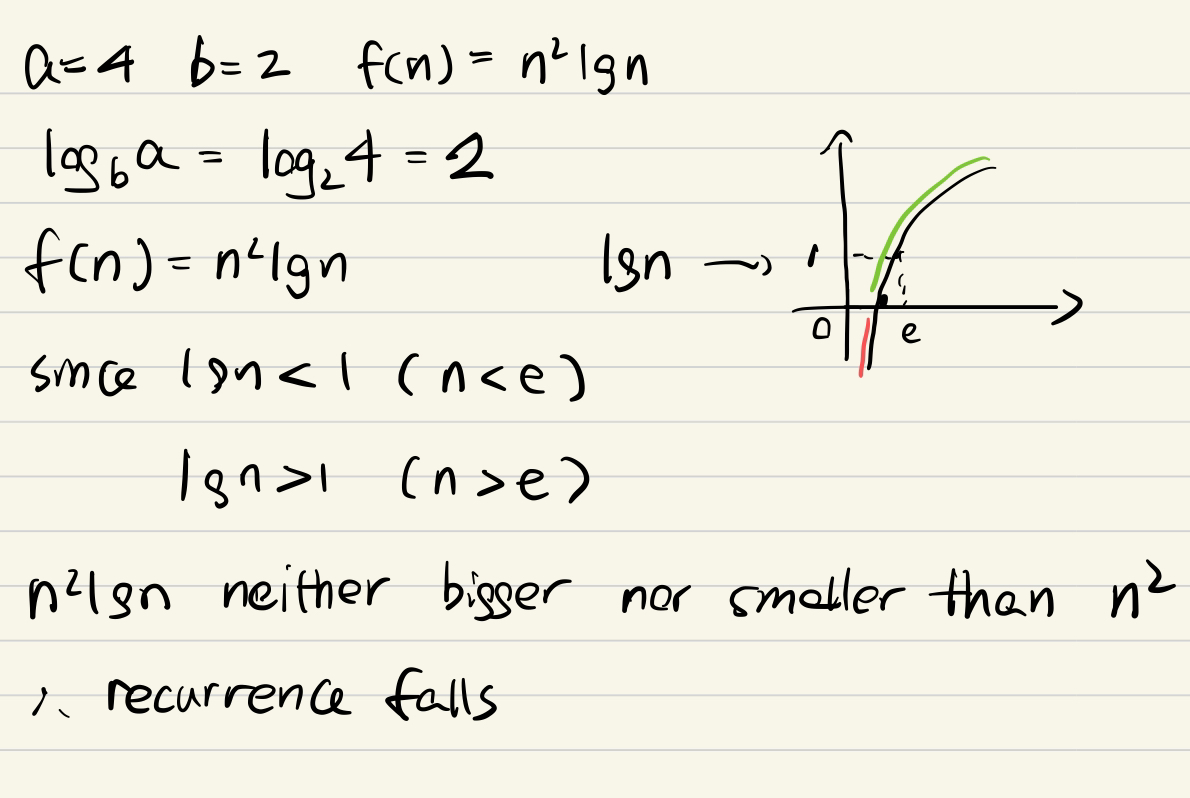
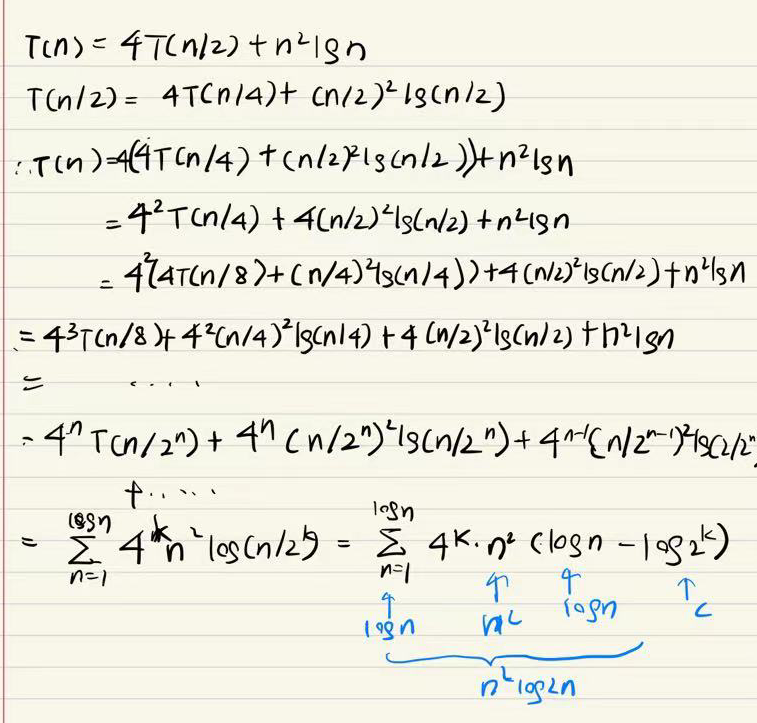
e.g6***不符合Master method
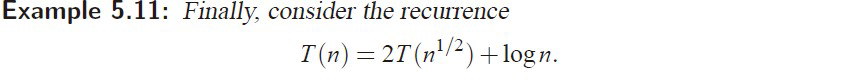


Matrix Multiplication 矩阵乘法???(暂时搁)
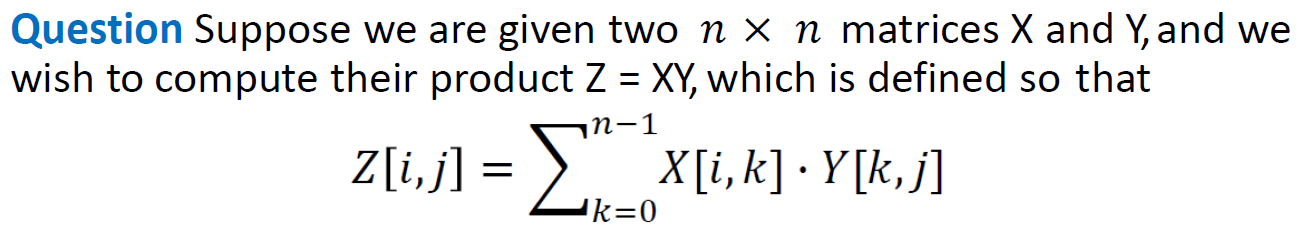
Counting inversion???(暂时搁)
Lec9 最优化问题
Knapsack 背包问题
fractional 背包
e.g1
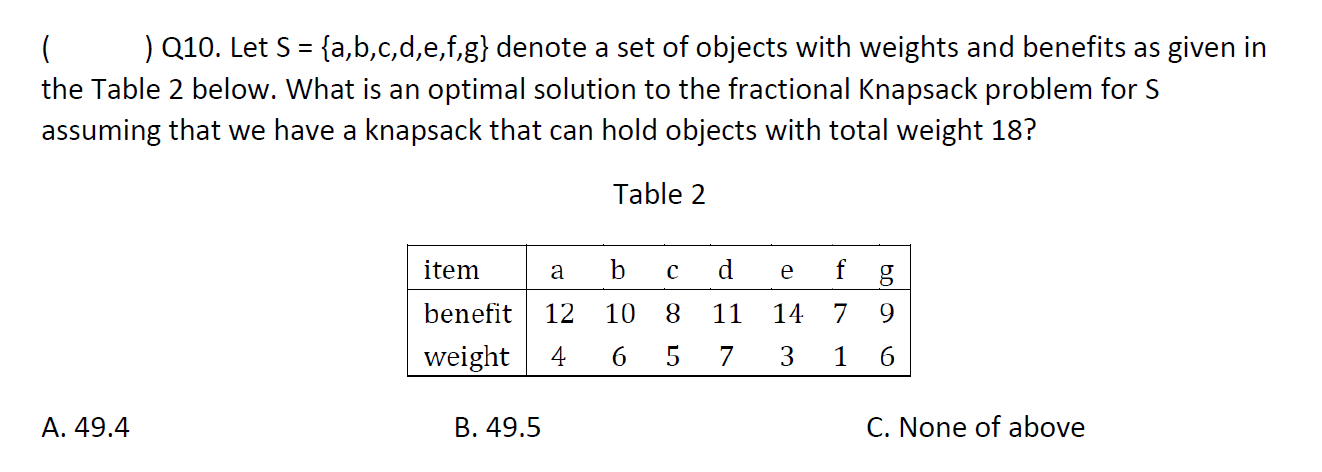
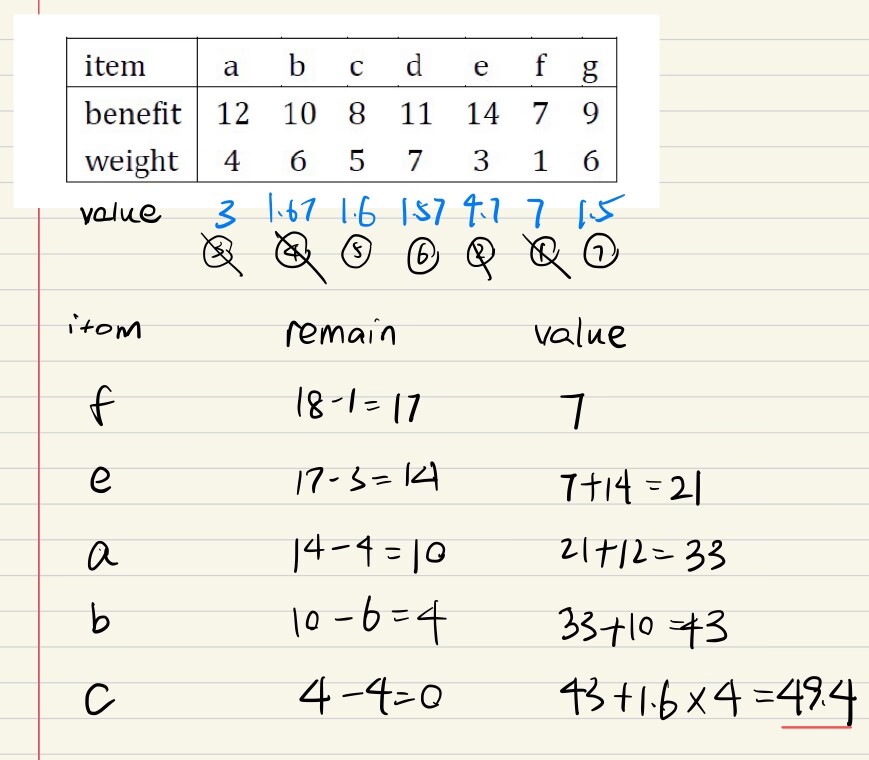
01背包
0/1背包问题-动态规划 Knapsack_problem Dynamic Programming_哔哩哔哩_bilibili
https://alchemist-al.com/algorithms/knapsack-problem
e.g1
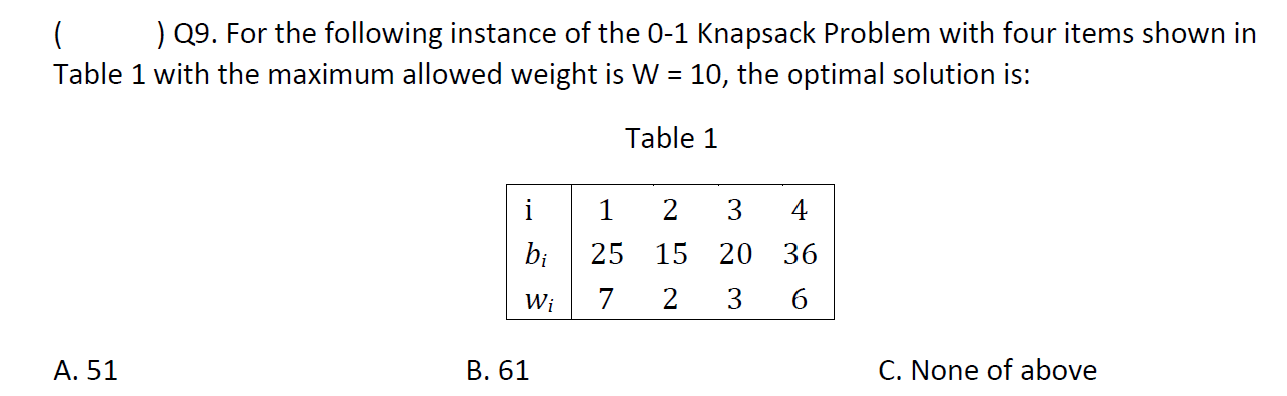
C
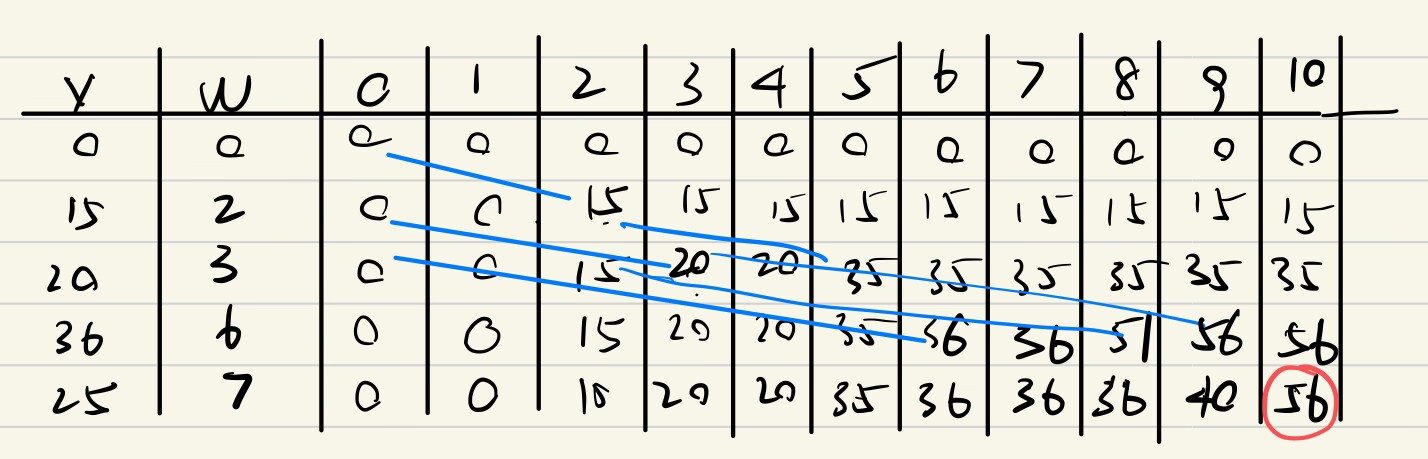
e.g2

我做的,我习惯先按照重量排序一下再算
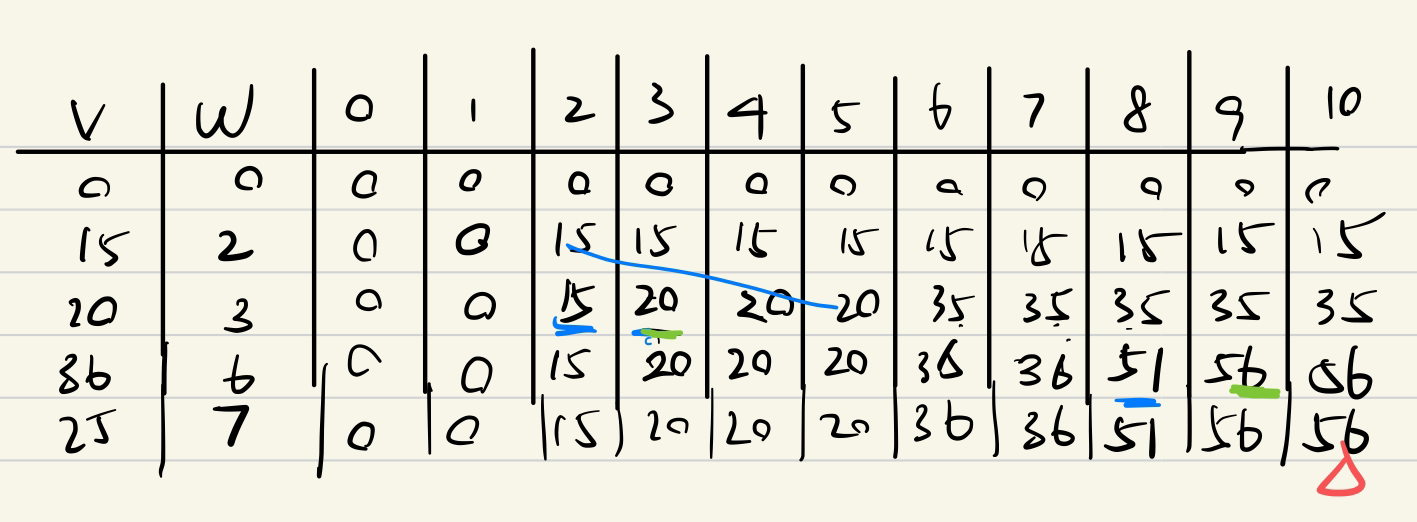
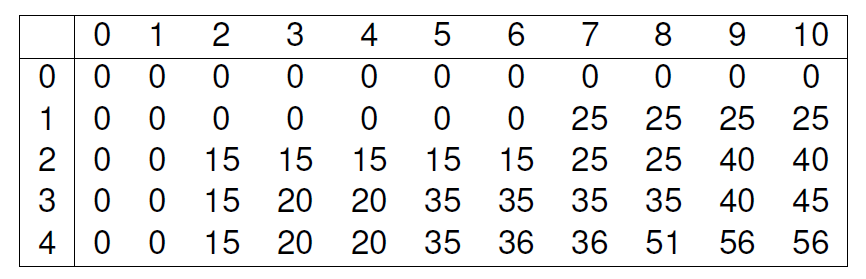
标答
Interval Scheduling 区间调度(暂时搁置)
大题***


Lec10 Graph
A graph𝐺=𝑉,𝐸consists of a set of vertices (nodes) V and a set of edges E, where each 𝑒∈𝐸 is specified by a pair of vertices 𝑢,𝑣∈𝑉
一些术语
End vertices:一条边的顶点
Edges incident:一个顶点相邻的边
Adjacent vertices:相邻的顶点
Degree:是指一个顶点连接的边的数量
Path:交替的顶点和边的序列,从顶点开始,以顶点结尾,每条边的前面和后面都有它的sendpoints
Simple Path:所有顶点和边都不相同的路径
subgraph:子图
acyclic graph: 没有 cycle的图。树是相互连接的acyclic graph
Directed acyclic graphs 有向无环图称为dag。不可能通过遍历这些边回到同一个节点。
-
最小生成树:用于找到一个图中连接所有顶点的最小权重的树。常用的算法包括Prim算法和Kruskal算法。这些算法主要关注于连接所有顶点,而不是特定的起点和终点。
-
最短路径:用于找到图中从一个顶点到另一个顶点的最短路径。常用的算法包括Dijkstra算法和Bellman-Ford算法。这些算法主要关注于找到从一个指定起点到一个指定终点的最短路径。
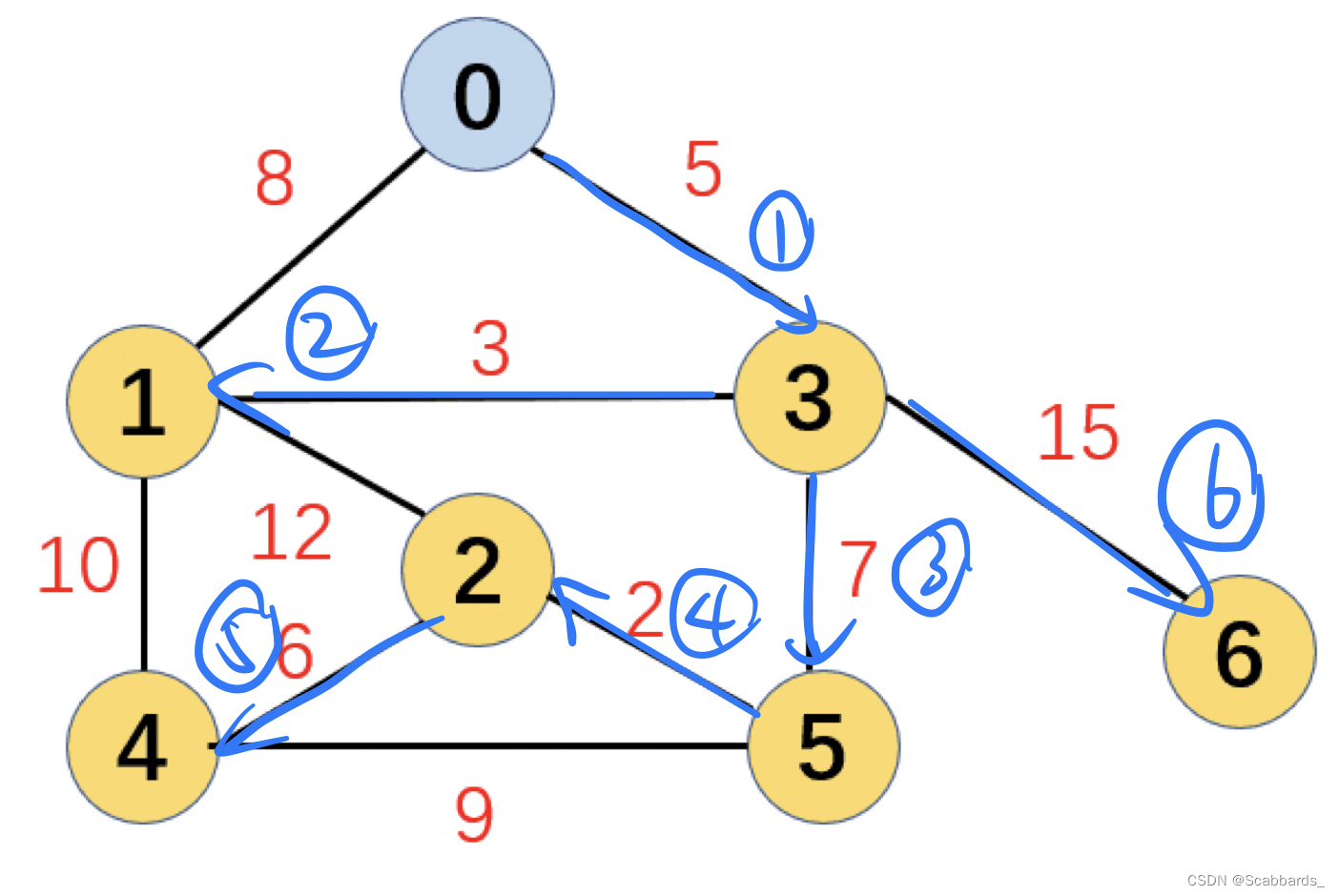
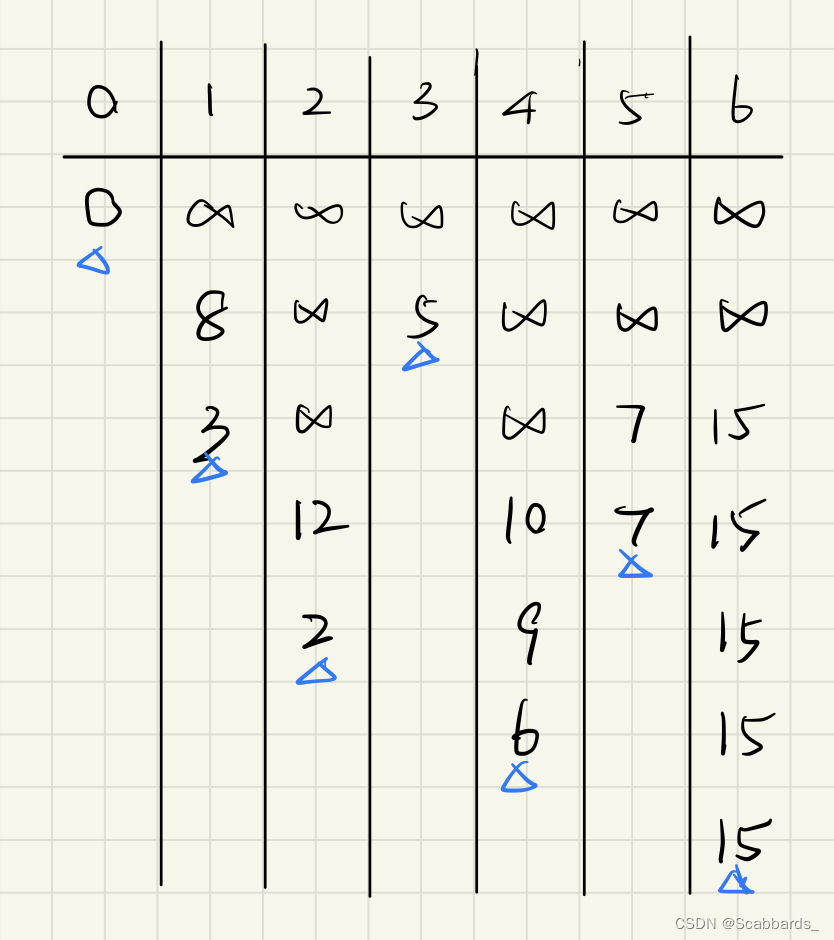
Dijkstra
记录总路径,当然是要从最短的来s

我自己做的
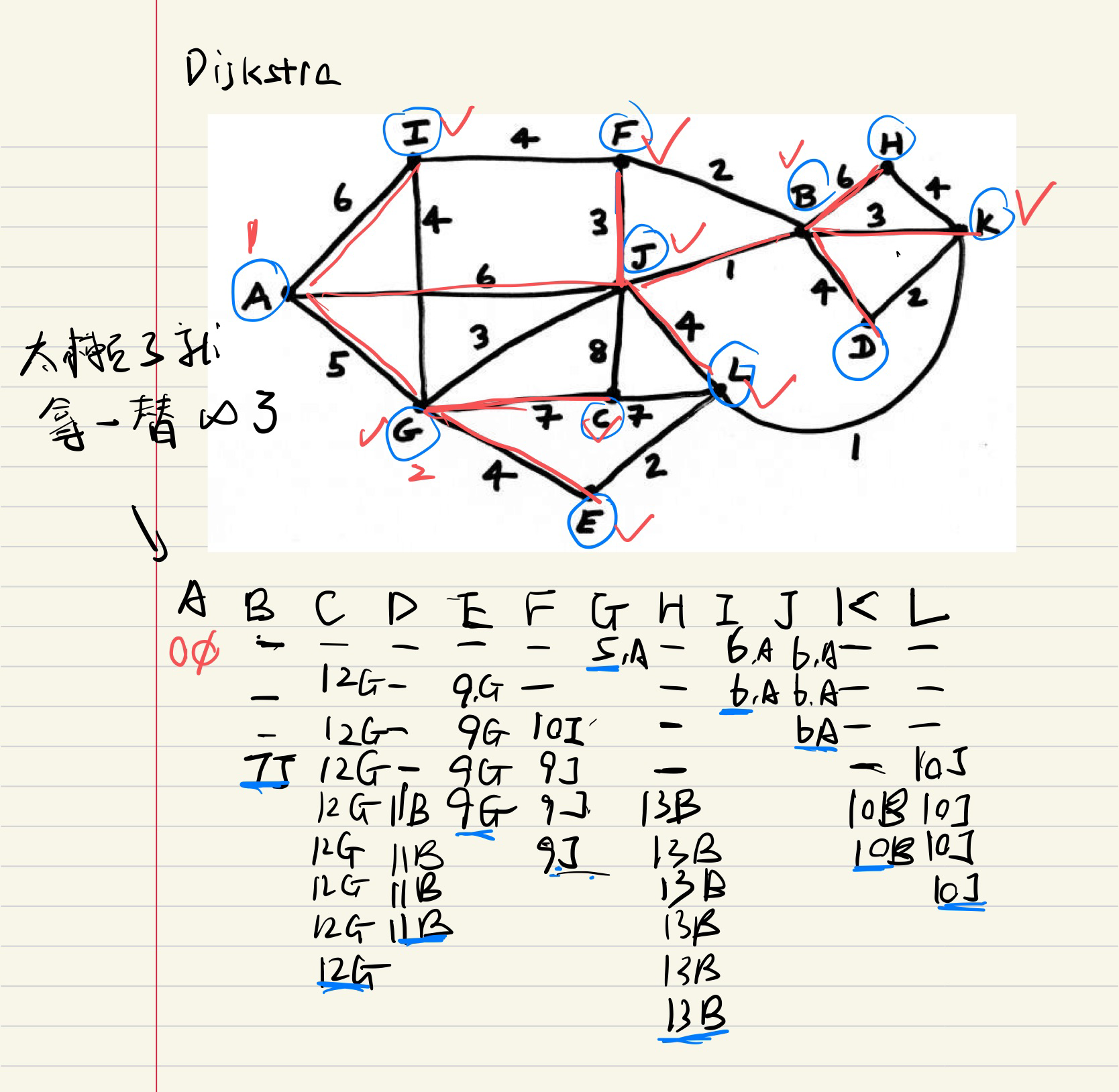
标答
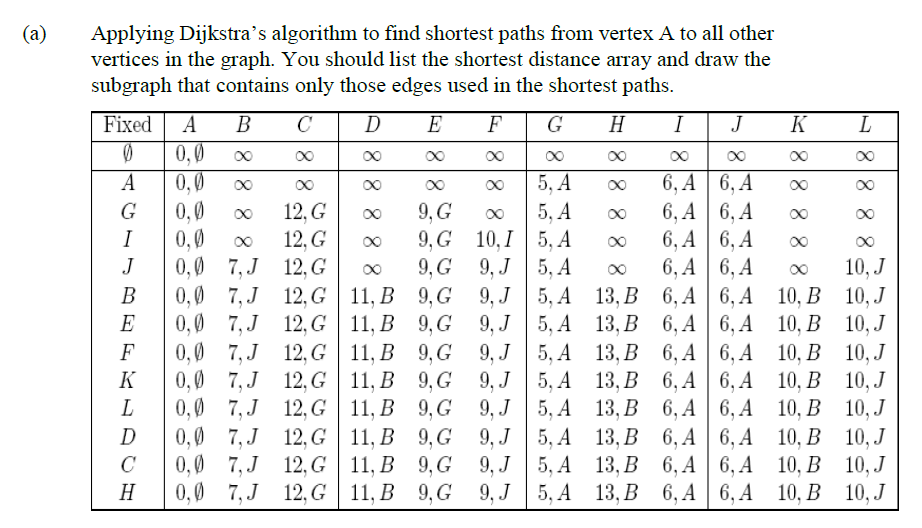
Bellman-Ford暂时没有例题
Kruskal
从最短的边开始选逐渐选到大边

我自己做的
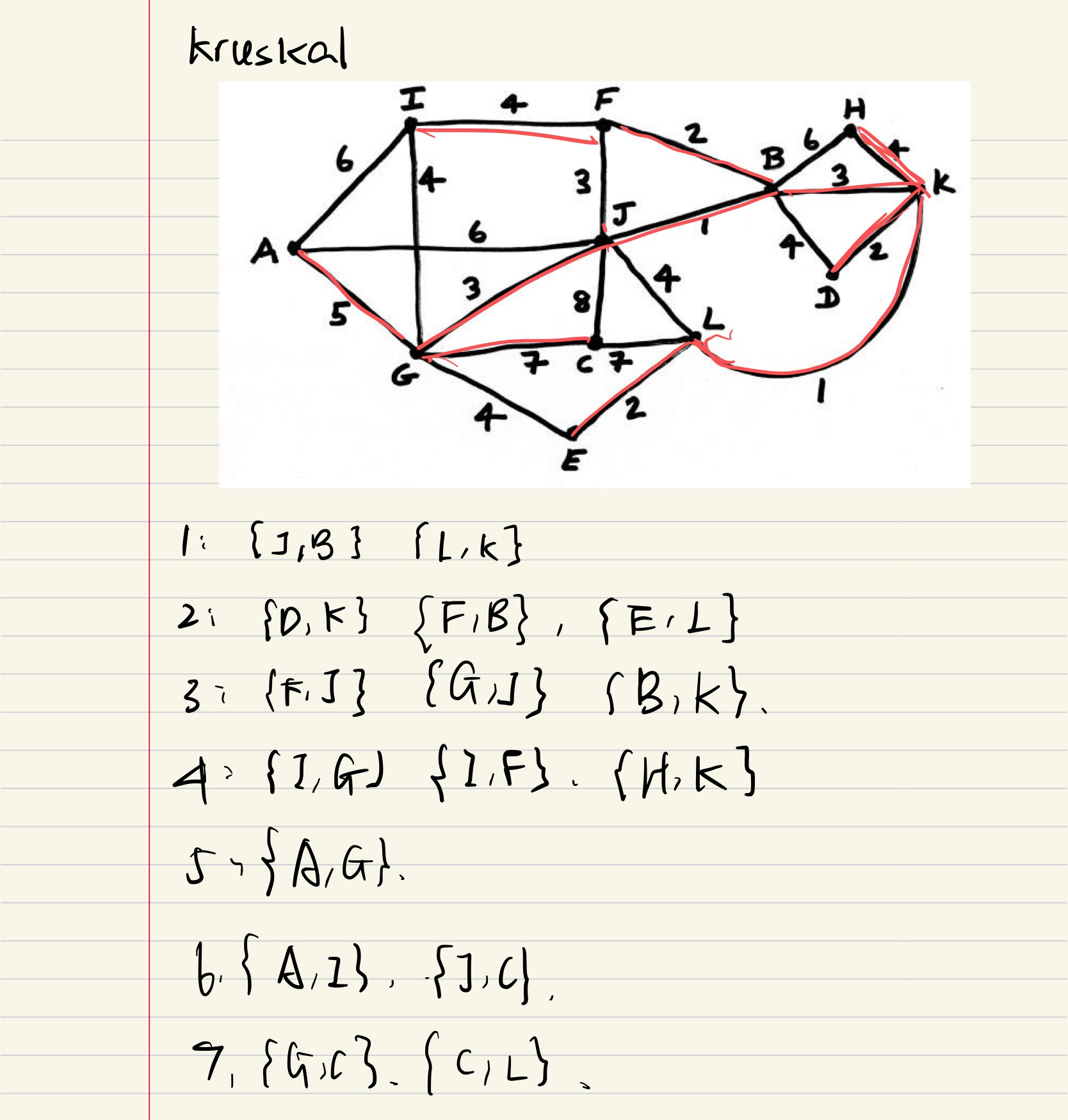
标答

Prim's algorithm 找最小生成树
1.选取权值最小边的其中一个顶点作为起始点。
2.找到离当前顶点权值最小的边,并记录该顶点为已选择。
3.重复第二步,直到找到所有顶点,就找到了图的最小生成树。
e.g1

自己写的
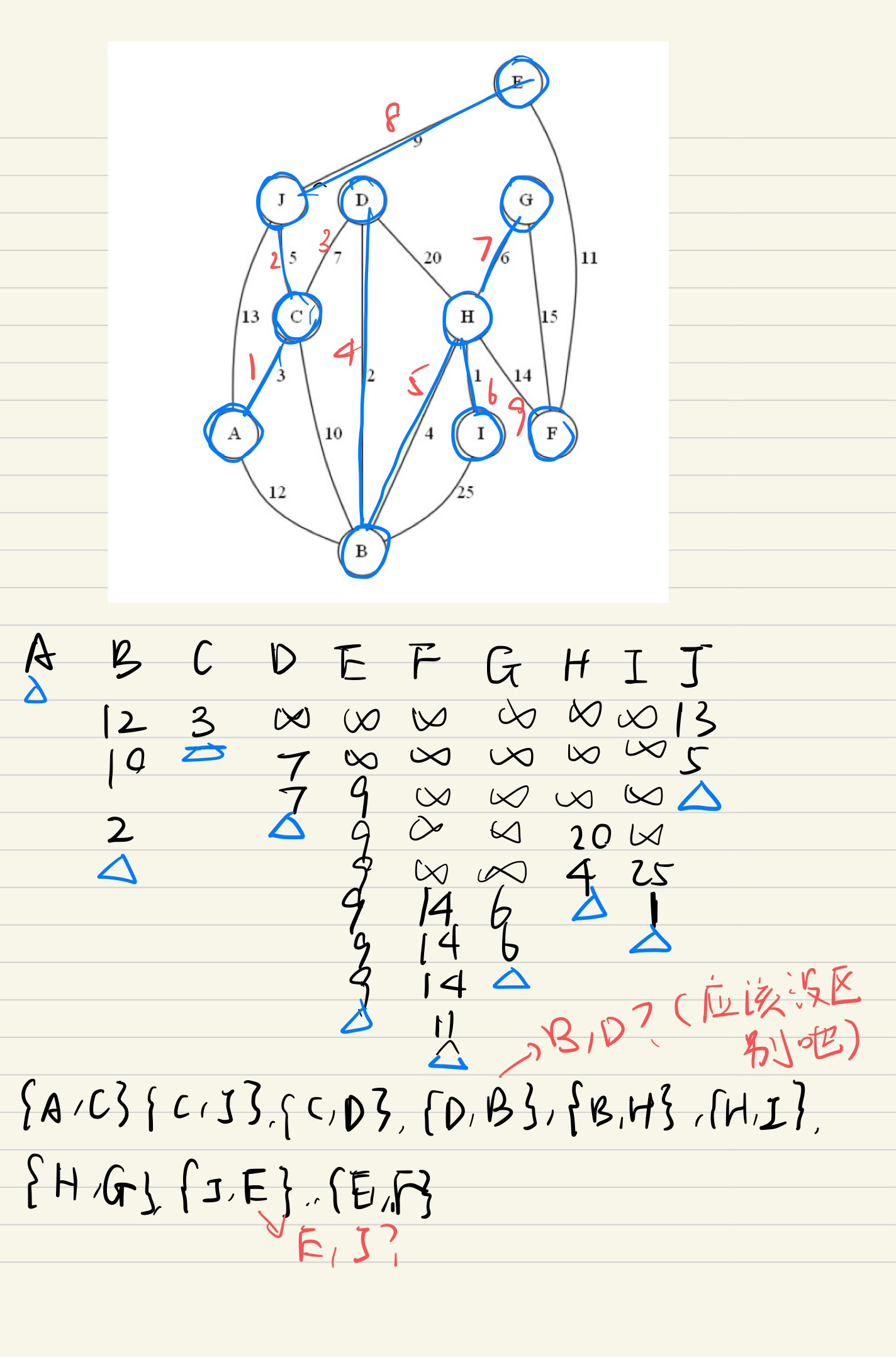
标答

e.g2
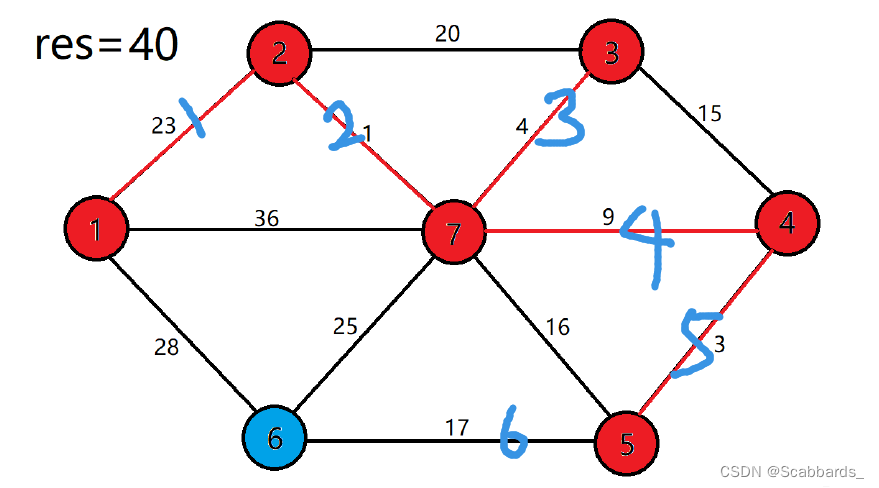

e.g3
BFS 定理证明
要是考试考这种证明我直接表演一个暴毙!

sol


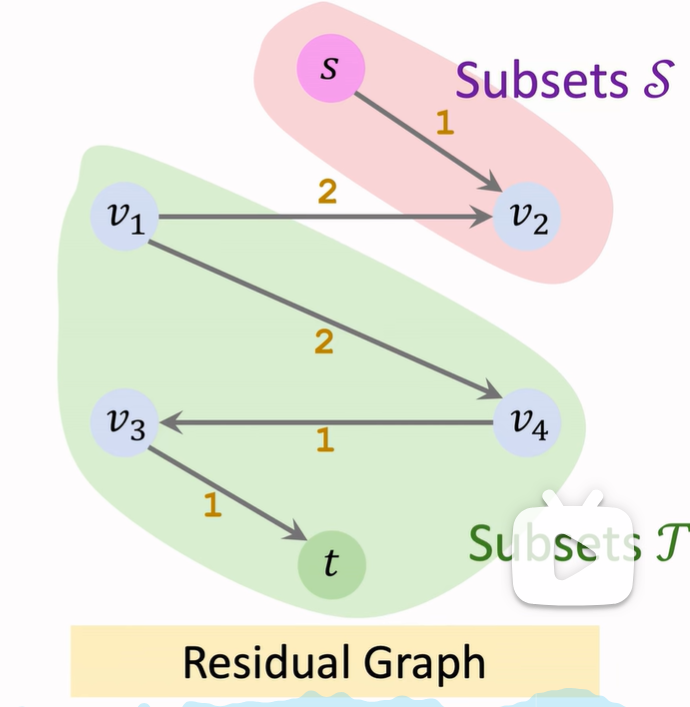
Lec11 Flow 流
-
增广路径(Augmenting Path):
从起点s到t的简单路径,其中不能有回路
-
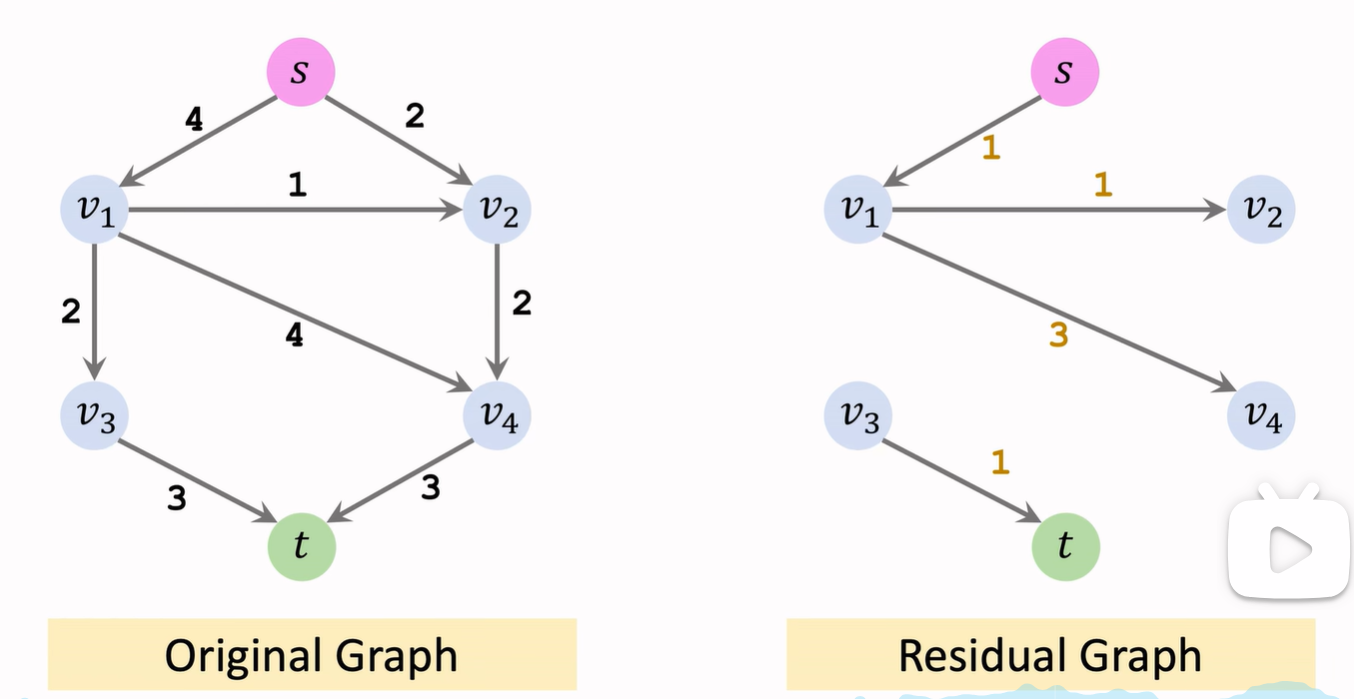
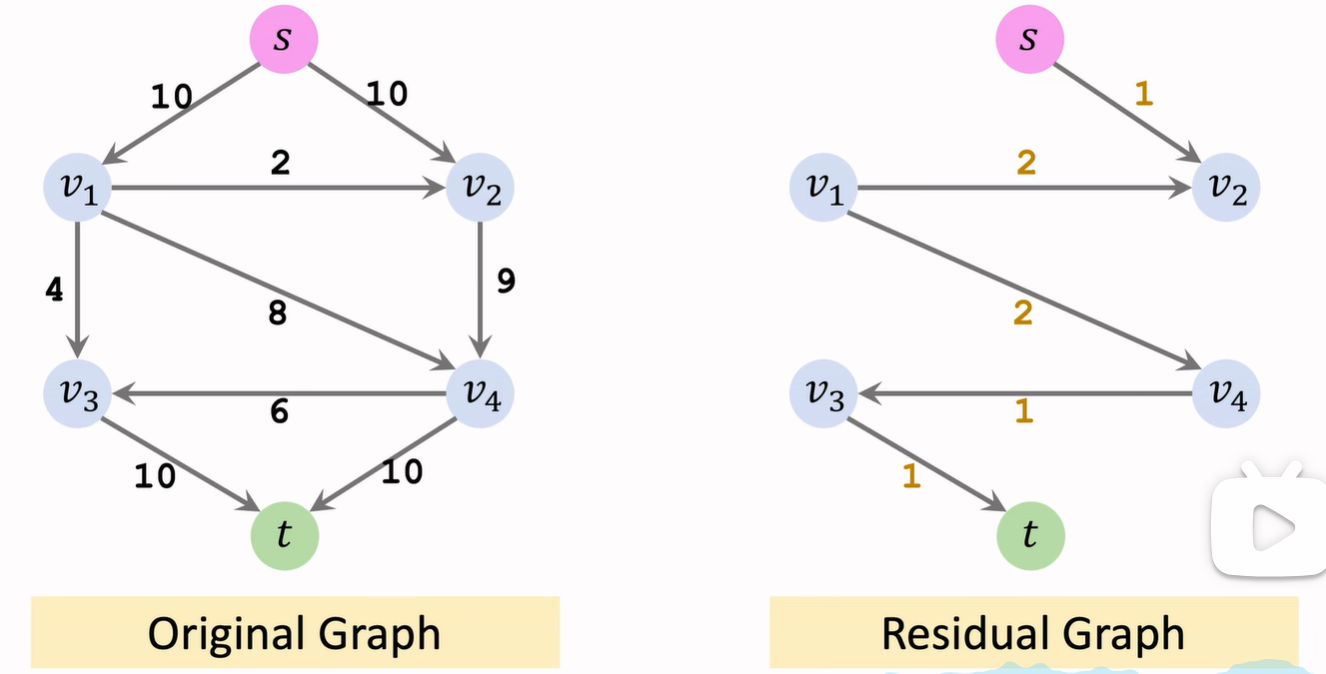
剩余网络(Residual Network):
- 剩余网络是在一个流网络中,根据当前流量情况所生成的一个新的网络。这个网络中的边表示原网络中的边上还能承载的额外流量。
- 对于每条边,我们可以通过减去流量(已经通过的流量)来得到该边的剩余容量。如果一条边的剩余容量大于 0,则在剩余网络中存在一条对应的边,表示从该边可以继续传送流量。
Ford-Fulkerson Algorithm
1.先找到augmenting path
- 添加backward path
e.g1
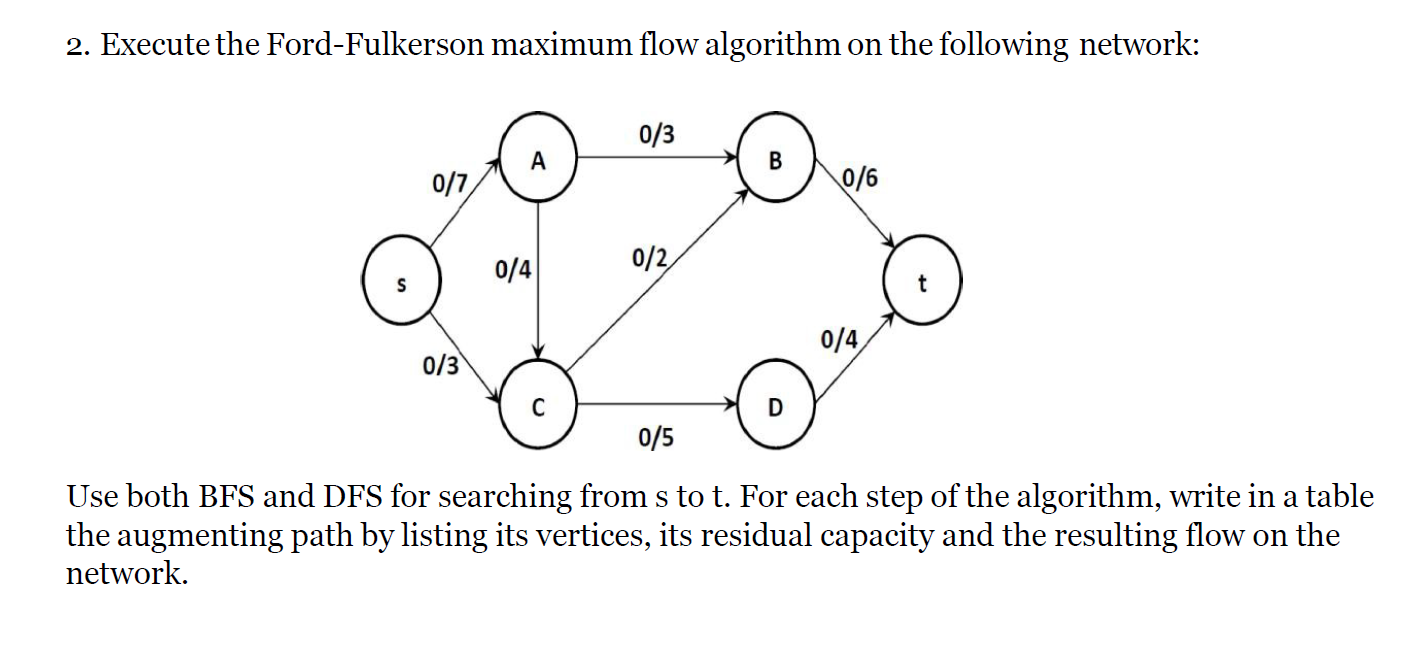
BFS 的逐层遍历特性确保了每一层的节点在下一层的节点访问前都被访问
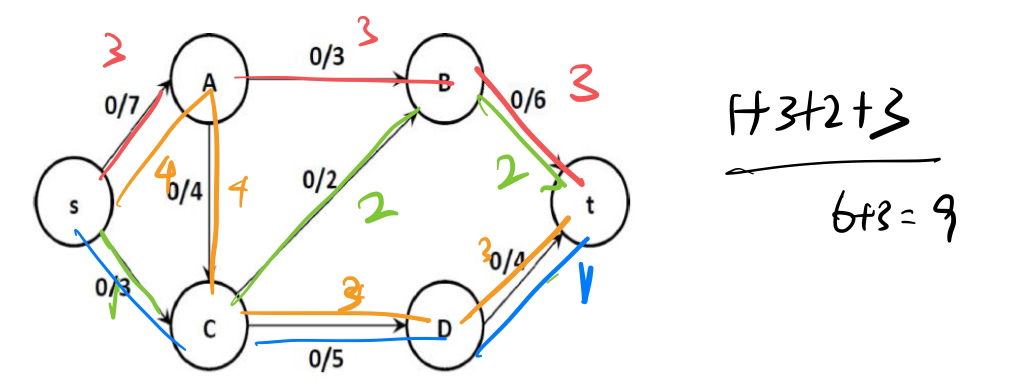

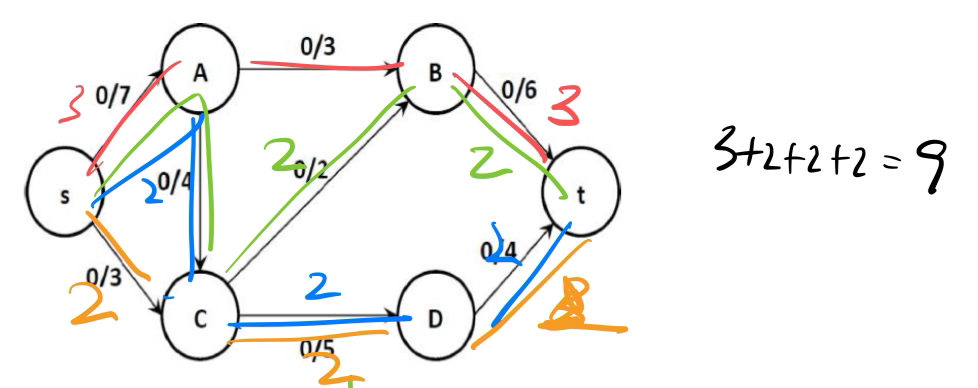

e.g2*


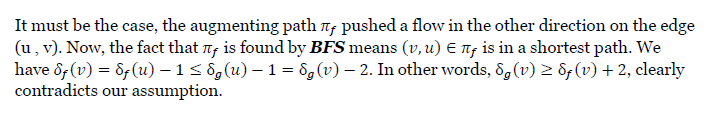
e.g3
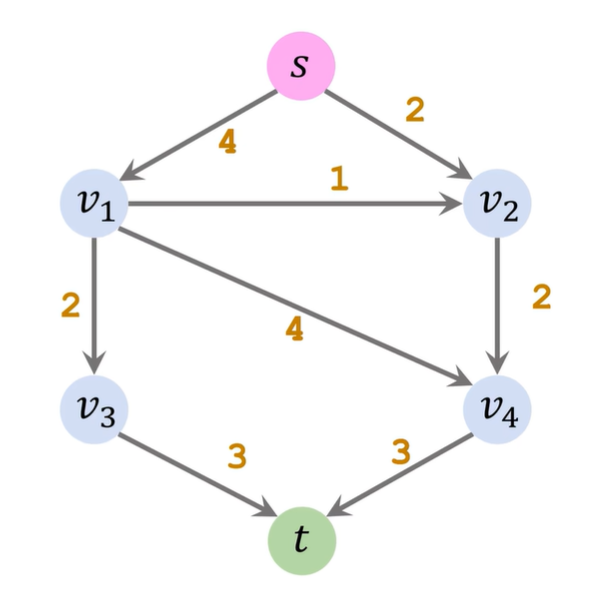

e.g4
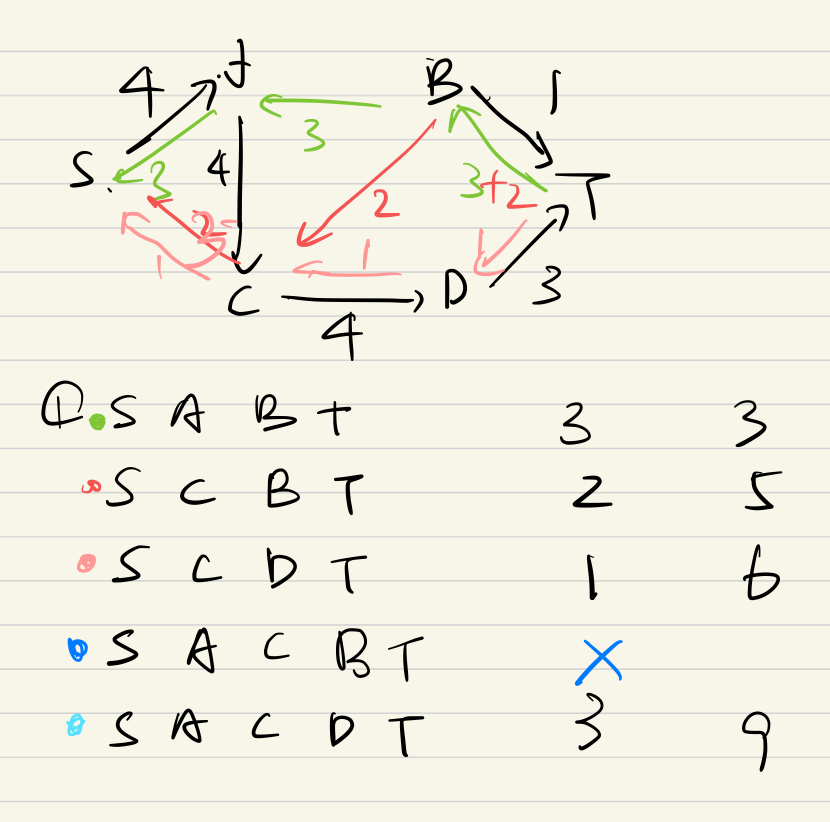
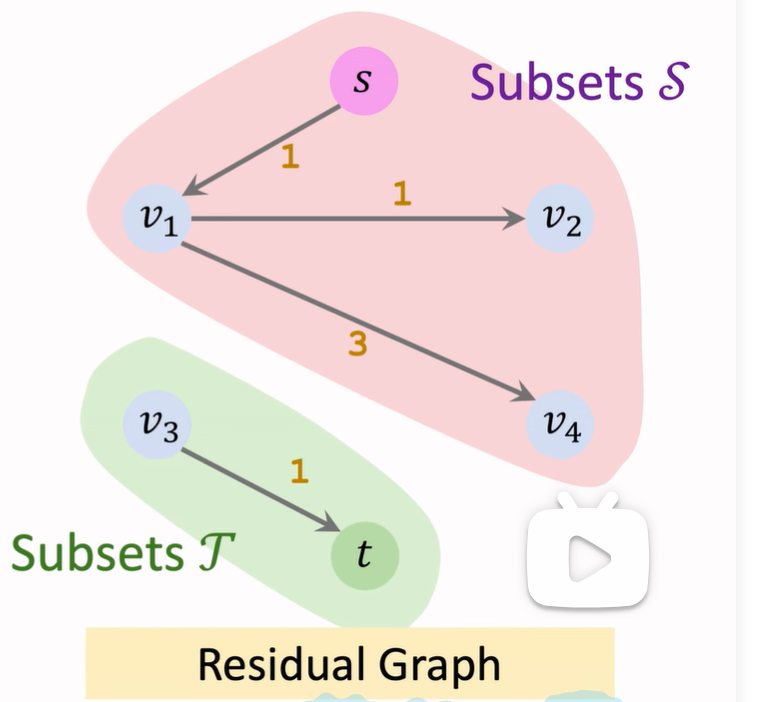
Min-cut
13-5: 最小割 Min-Cut_哔哩哔哩_bilibili
把原有集合分割成两个部分,Min cut是让总割断的水管最小,让水无法流往终点
注意,最小割不唯一
最大流最小割问题:最大流的流量等于最小割的容量

Lec13 Modular-Arithmetic
感觉Lec13和Lec14都能看这个我们的《密码学的数学基础》到底都介绍哪些内容,难不难_哔哩哔哩_bilibili
首先有个很重要的概念 x(mod y) 这种形式表示的是x除以y得到的余数
Euclidean algorithm
这个方法也叫辗转相除法,用来计算两个数的最大公因数。
欧几里得演算法(辗转相除法)_哔哩哔哩_bilibili 这个讲的很好的
拿大数/小数直到没有余数为止
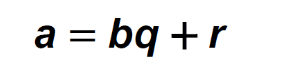
e.g1
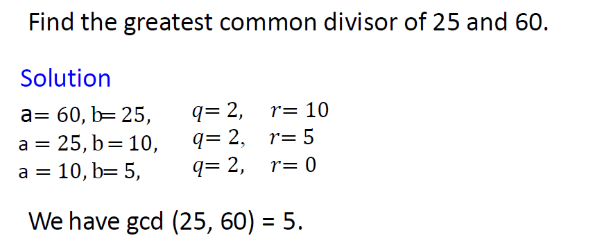
e.g2
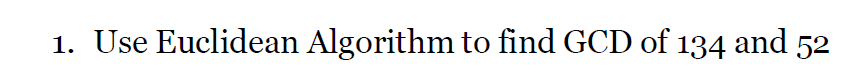

Extend Euclidean 拓展欧几里得/广义欧几里得
用欧几里得计算中每一步的出来的余数和商,用于计算sa +tb = gcd(a,b)中的s和t

r = a - c*b,然后通过前面的式子把a和b换掉
e.g1
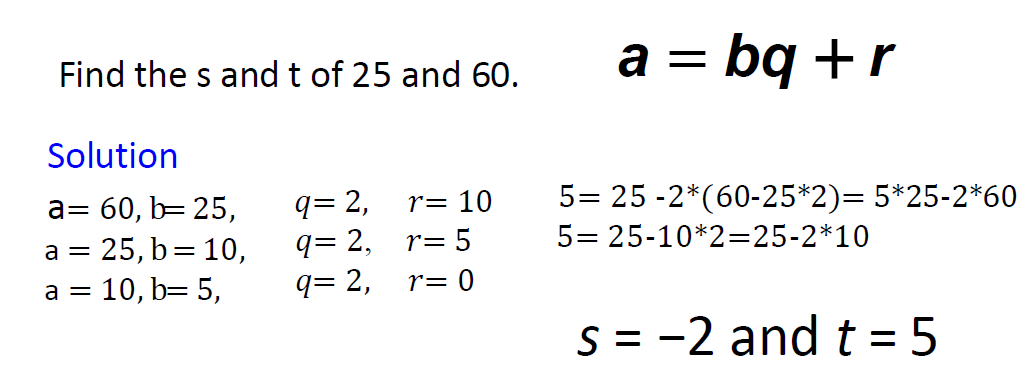
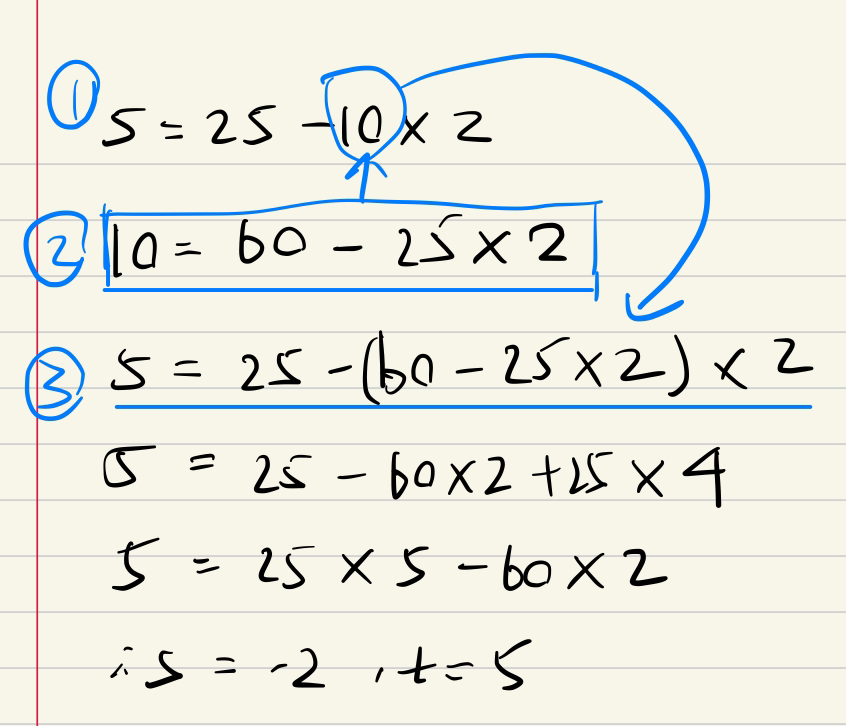
e.g2
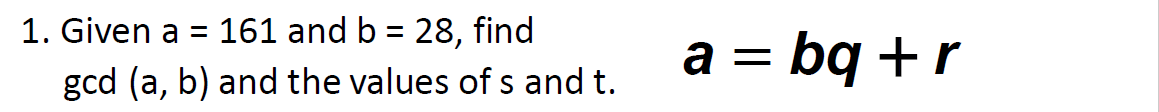
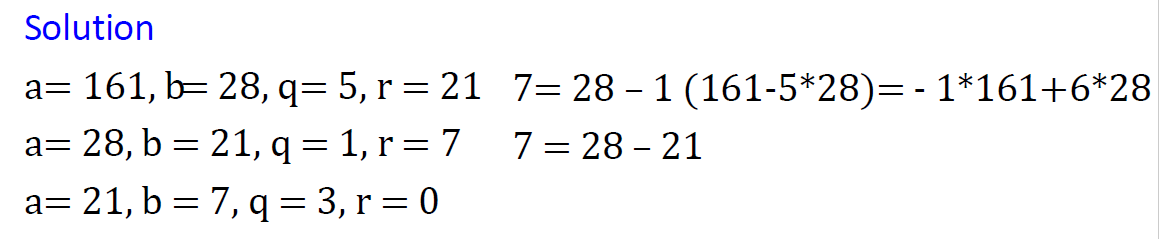
e.g3
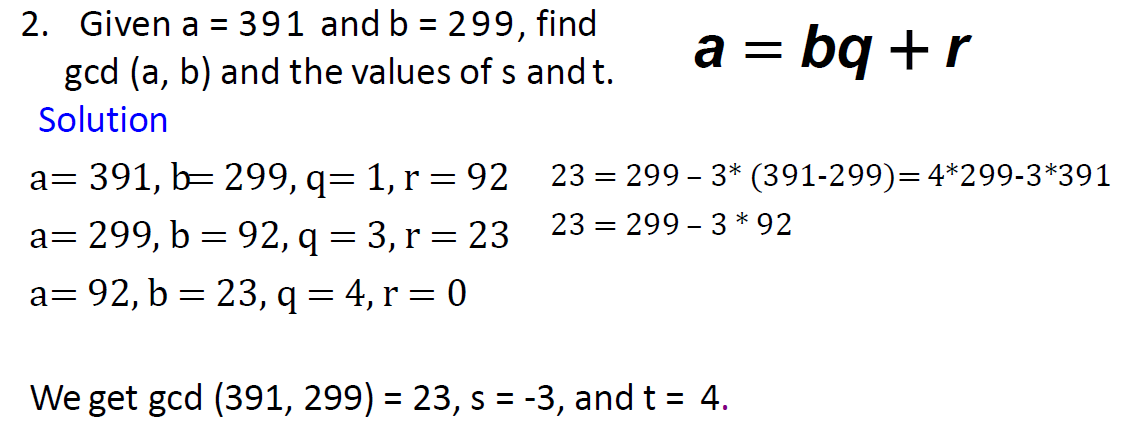
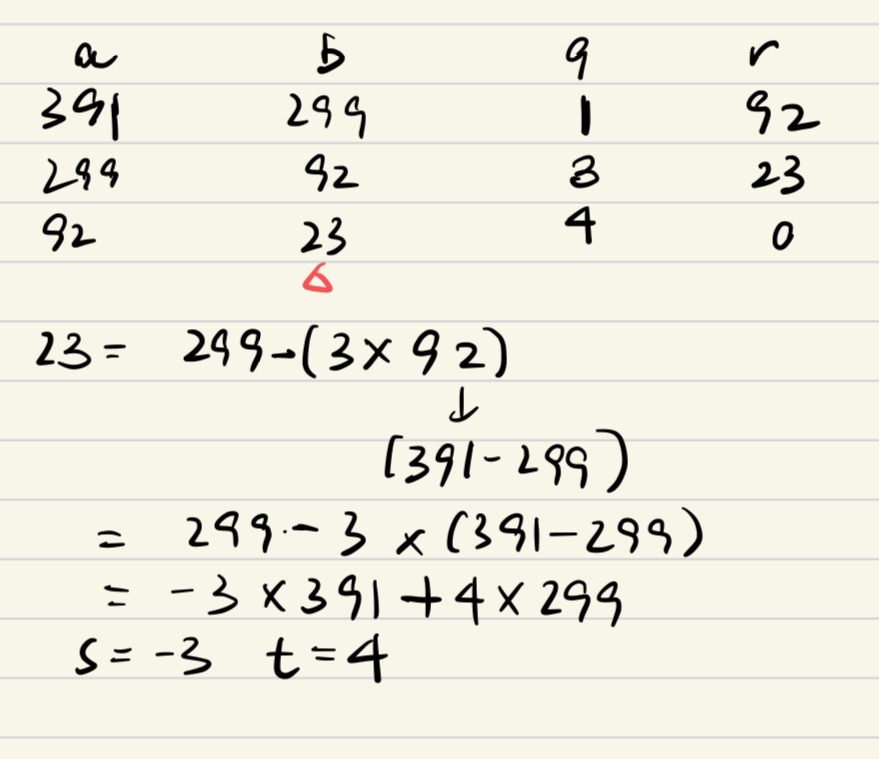
e.g4

我做的

标答(写的好复杂噢)

Multiplicative Inverse 乘法逆元
乘法逆元在数论和抽象代数中是一个重要的概念,特别是在模运算(模算术)中有广泛应用。给定一个整数 a和一个模数 m,如果存在一个整数 x使得
a ⋅ x ≡ 1(mod m)
怎么找b在a乘法逆元:
1)先找到as + bt = 1 中的s和t(用拓展欧几里得)
所以ab互质是充要条件,充要条件哈
2)t可能得到一个负数,但是可以通过 t ≡ u(mod m)
这个u就是最终答案
e.g1


e.g2
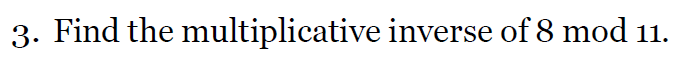

标答

Liner congruence
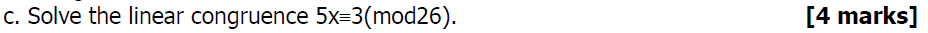
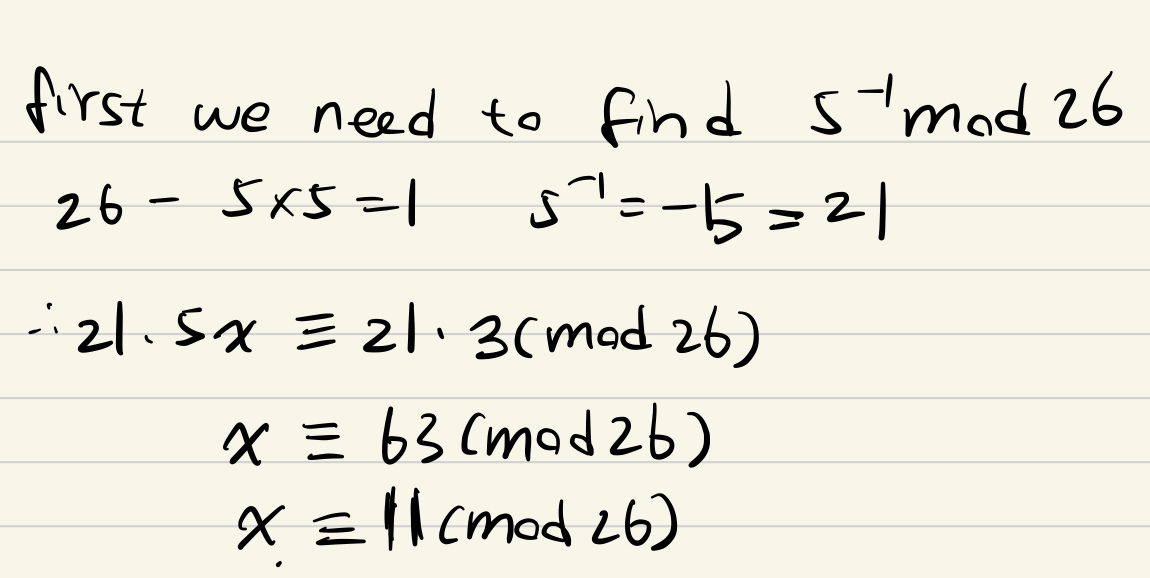
模运算的性质

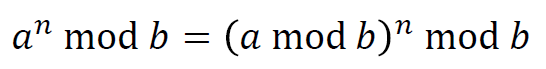
e.g1**
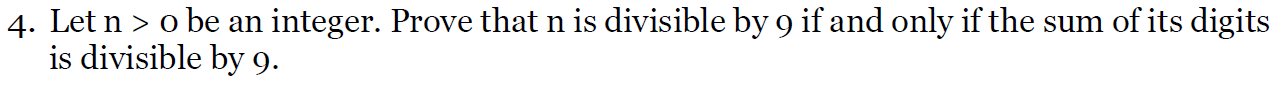
我自己写的
老师标答
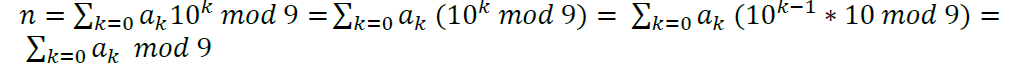

e.g2**
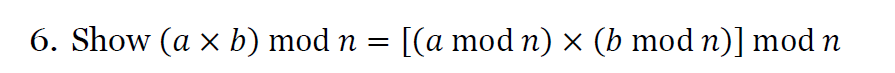
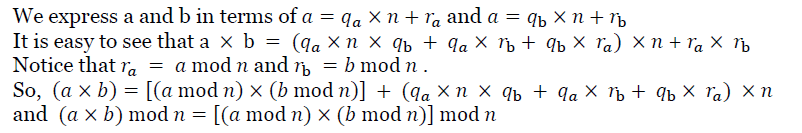
Fast Modular Exponentiation**

从前往后加
e.g1

彼阳的ppt写的变来变去的搞得我整了老半天,就不放老师ppt上的了,变你🐎呢推了我一个小时结果发现原来很简单

Euler's Theorem
ϕ是一个数学函数,用来计算小于等于某个正整数 n 的正整数中,与 n 互质的数的个数

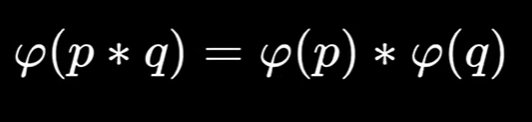


这里p是质数↑
e.g1
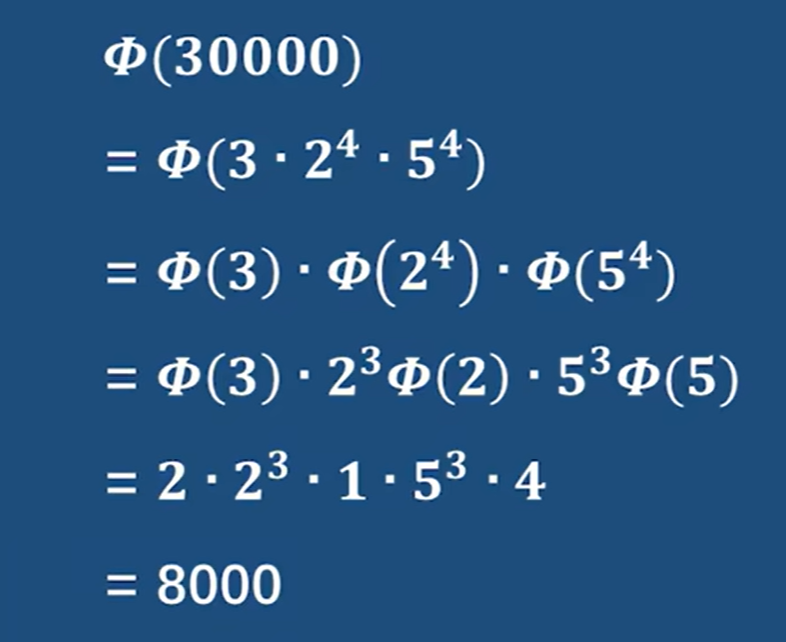
e.g2
这题是乘法逆元和欧拉定理的综合考察

sol

费马小定理********
e.g1


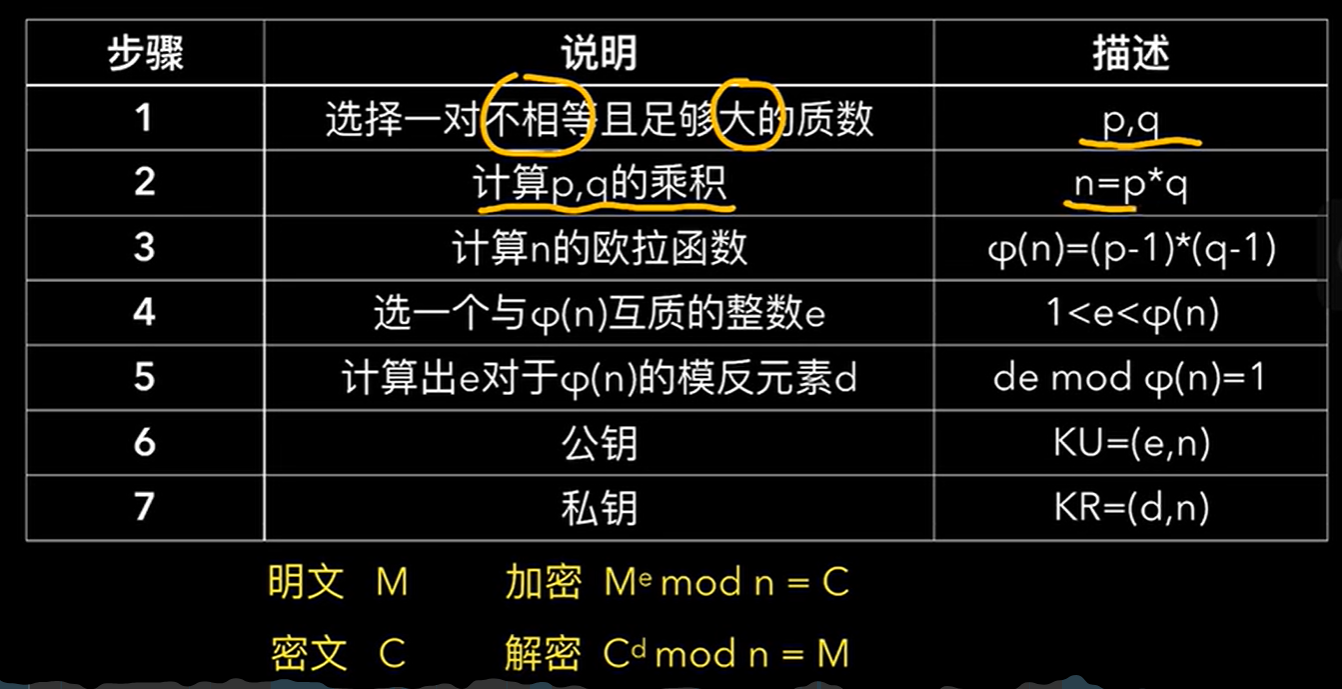
RSA 非对称加密
【RSA加密算法】| RSA加密过程详解 | 公钥加密| 密码学| 信息安全|_哔哩哔哩_bilibili
public modulus(公钥模数),是pq的乘积
很好的视频,使我的大脑旋转
e.g1
e=3和p=17,q=23 是公钥,求私钥d
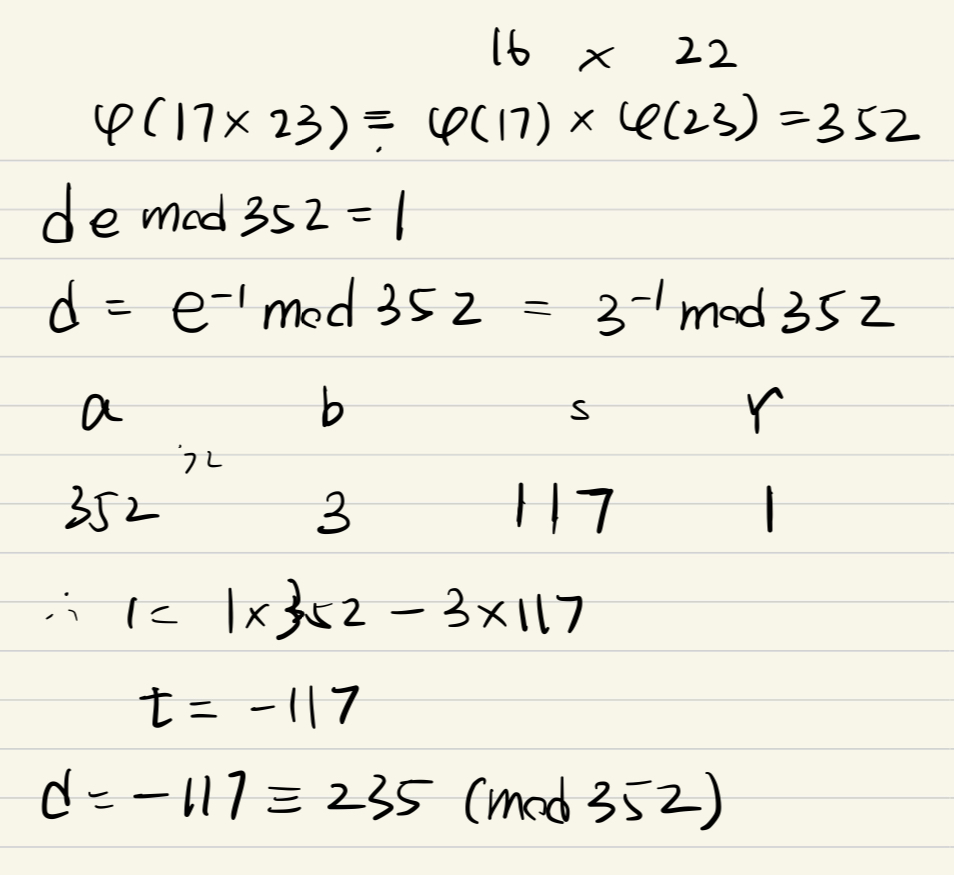
e.g2


老师标答
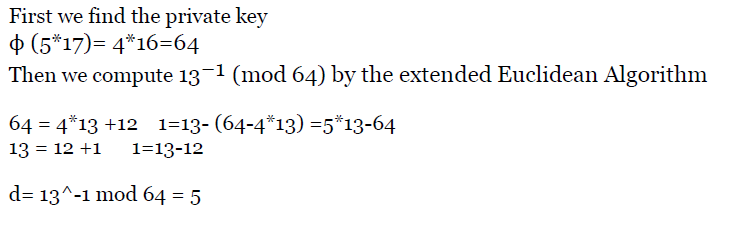

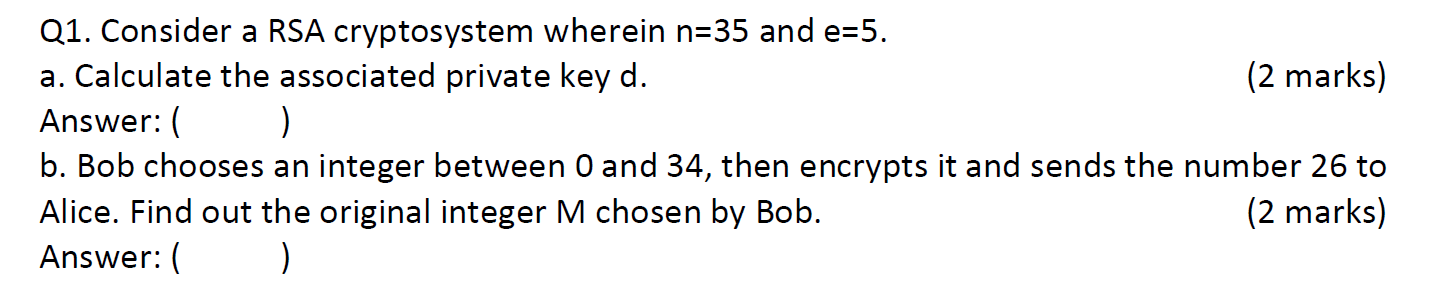
e.g3

e.g4





Lec15 P,NP
期末复习的时候看到这个老师的视频,醍醐灌顶了属于是13.1 NP问题概述_哔哩哔哩_bilibili
刘老师,你学学人家
P: P类问题是指可以在多项式时间内(即时间复杂度为多项式函数的时间内)解决的问题。
NP: NP类问题是指能够在多项式时间内验证其解的问题。即使找到一个解可能很难,但一旦有了一个解,验证其正确性可以在多项式时间内完成。因为P类问题能在多项式时间内验证,所以P问题是NP问题,但是NP问题不一定是P问题
最优化问题(Optimization)转化成判定性问题
**NP-complete:**NP中最难的问题,所有NP都可以规约(reducibility,实例对应,输出一致,传递)到NPC问题,是NP-hard的子集
**NP-hard:**多项式时间内不一定能验证
SAT
中文名叫做合取范式CNF的可满足性问题SAT,是NPC问题
3-SAT
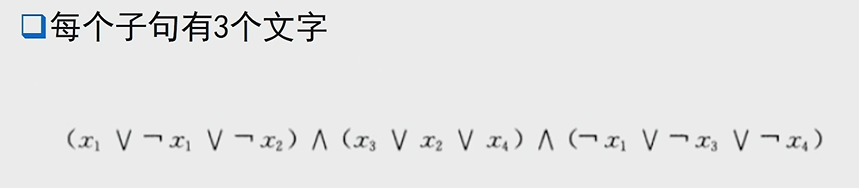

注意,2-SAT是P问题,3-SAT是NPC


e.g1

很好我也不会证,于是请教了万能的chatgpt
标答

e.g2 3-SAT规约
这道题是把一个四合取范式规约成一个3CNF

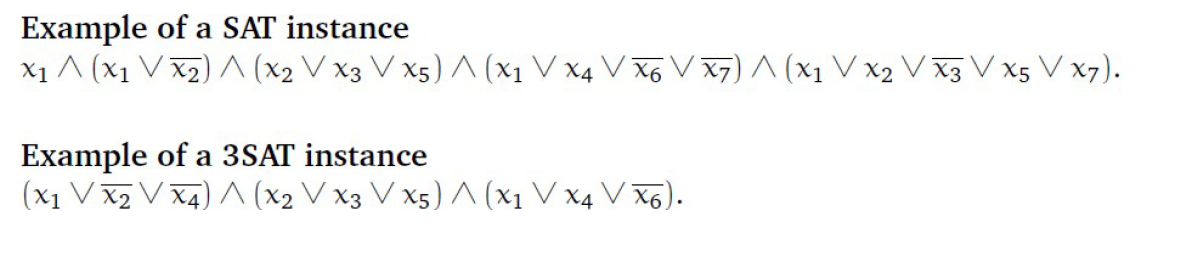
sol

e.g3
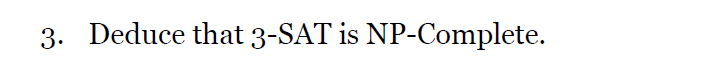

e.g4
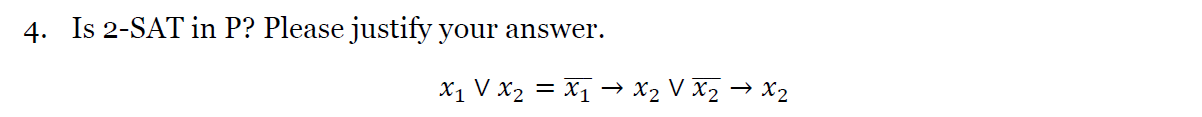
Yes,
公式可满足
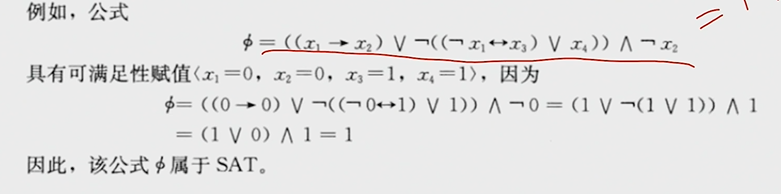
step1. 证明是个np问题

2.可满足性
- 一致性
e.g5


顶点问题

Hamitonian cycle



综合题
e.g1




e.g2



e.g3