在计算机中,小数点及其位置并不是显式表示出来的,而是隐含规定的。根据小数点的位置,可以分为两类:定点数和浮点数。
1 定点数
小数点的位置是固定不变的。根据小数点的具体位置,又可以分为两类:定点小数和定点整数。
定点小数
小数点隐含固定在最高数据位的左边,整数位表示符号位,用于表示一个纯小数。

定点整数
小数点隐含固定在最低数据位的之后,整数位表示符号位,用于表示一个纯整数。

2 浮点数
小数点的位置由阶码确定,因此是浮动的!用于表示实数。在计算机中,通常将浮点数拆分长阶码(exponent)和尾数(mantissa)两部分表示。尾数是规格化的纯小数。
x f p = 尾数 × 基 数 阶码 x_{fp} = 尾数 \times 基数^{阶码} xfp=尾数×基数阶码
举个例子:
( 11100.101 ) 2 = 0.11100101 × 2 5 = 0.11100101 × 2 101 (11100.101)_2 = 0.11100101 \times 2^5 = 0.11100101 \times 2^{101} (11100.101)2=0.11100101×25=0.11100101×2101
其实写法和十进制的科学记数法一致。
0.11100101 × 2 101 0.11100101 \times 2^{101} 0.11100101×2101实际上是由两个定点数组成,分别是(1)表示阶码的定点整数;(2)表示尾数的定点小数。

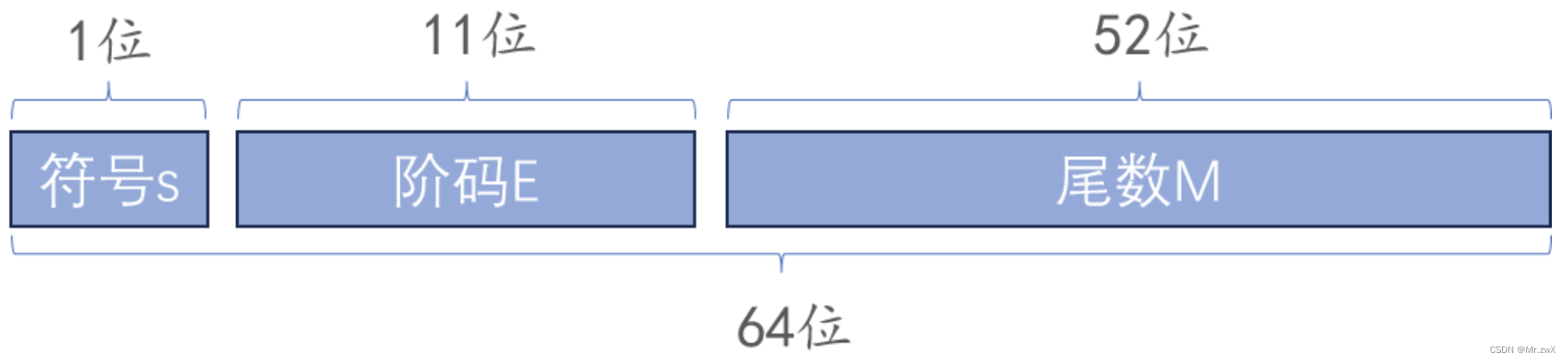
浮点数的一般存储格式:

16位浮点数(简单例子)
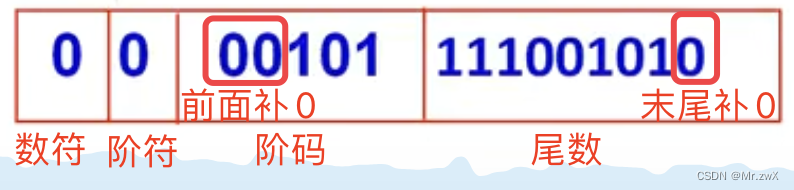
16位浮点数的格式:阶码是5位,尾数是9位,数符和阶符分别是1位。
举个例子:实数28.625的浮点表示。
N = 28.625 = ( 11100.101 ) 2 = ( 0.11100101 ) 2 × 2 5 N = 28.625=(11100.101)_2=(0.11100101)_2\times2^5 N=28.625=(11100.101)2=(0.11100101)2×25
IEEE 754标准(重点掌握🌟)
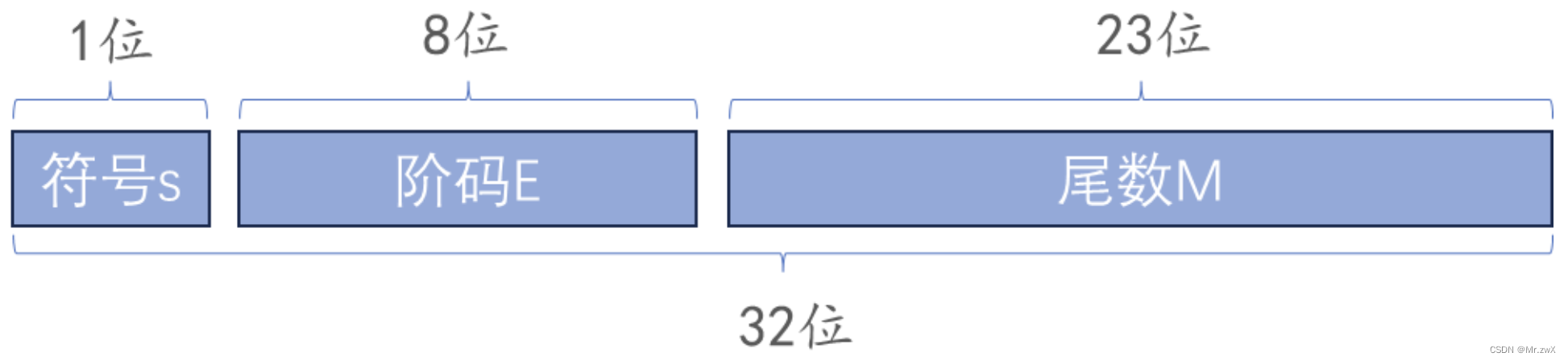
IEEE 754总共用32位对浮点数进行存储,被划分成了三个部分:(1)符号位S;(2)阶码E;(3)尾数M。
- 符号位S:0 = 正数,1 = 负数
- 阶码E:浮点数被二进制科学表示法规范化后的指数,阶码采用移码表示(也就是有个偏置)
- 尾数M:被二进制规格化后要求小数点前一位数必须为1,由于所有的浮点数都采用这样的方式进行处理,所以尾数中实际隐含了最高位1,例如尾数为M,则实际在还原时,相当于是1.M
于是,已知S、E和M,我们可以得到浮点数为:
x f p = ( − 1 ) S × 1. M × 2 E − 偏置 x_{fp} = (-1)^S\times 1.M \times 2^{E-偏置} xfp=(−1)S×1.M×2E−偏置
注意,在单精度浮点数中,偏置=127。
浮点数 => IEEE 754
现在直观看一下如何将十进制浮点数转换为IEEE 754标准表示。已知一个十进制数85.125,求IEEE 754表示。
- 步骤1:将十进制数转二进制数,即 85.125 = ( 1010101.001 ) 2 85.125=(101 0101.001)_2 85.125=(1010101.001)2
- 步骤2:进行规范化,即 ( 1.010101001 ) 2 × 2 6 (1.010101001)_2 \times 2^6 (1.010101001)2×26
- 步骤3:确定符号位S=0,阶码 E = 6 + 127 = 133 = ( 10000101 ) 2 E=6+127=133=(10000101)_2 E=6+127=133=(10000101)2,尾数 M = 010101001 M=010101001 M=010101001(注意:M要省略掉小数点前的1)
- 步骤4:写出完整的IEEE 754表示,即 0 ∣ 10000101 ∣ 01010100100000000000000 0|10000101|01010100100000000000000 0∣10000101∣01010100100000000000000(注意:如果E不满8位,则在前面补0,如果M不满23位,则在后面补0)
IEEE 754 => 浮点数
已知一个IEEE 754表示是C1 51 00 00,求对应的十进制浮点数。
- 步骤1:展开IEEE 754表示,即 1 ∣ 10000010 ∣ 10100010000000000000000 1|1000 0010|101 0001 0000 0000 0000 0000 1∣10000010∣10100010000000000000000
- 步骤2:确符号位S=1为负,阶码 E = ( 10000010 ) 2 = 130 E=(1000 0010)_2=130 E=(10000010)2=130,尾数 M = ( 10100010000000000000000 ) 2 = . 6328125 M=(101 0001 0000 0000 0000 0000)_2=.6328125 M=(10100010000000000000000)2=.6328125(注意:尾数算出来的十进制数是小数位,前面隐含了1.)
- 步骤3:带入公式,即 x f p = ( − 1 ) S × 1. M × 2 E − 偏置 = − 1 × 1.6328125 × 2 130 − 127 = − 13.0625 x_{fp} = (-1)^S\times 1.M \times 2^{E-偏置}=-1\times 1.6328125 \times 2^{130-127}=-13.0625 xfp=(−1)S×1.M×2E−偏置=−1×1.6328125×2130−127=−13.0625
补充一下双精度浮点数的表示方式,转换方式和单精度类似,这里就不赘述了。