ABC357总结
A - Sanitize Hands
翻译
有一瓶消毒剂,正好可以消毒 \(M\) 双手。
\(N\) 名外星人陆续前来消毒双手。
\(i\) 个外星人( \(1 \leq i \leq N\) )有 \(H_i\) 只手,想把所有的手都消毒一次。
请计算有多少个外星人可以给所有的手消毒。
在这里,即使开始时没有足够的消毒剂给一个外星人的所有手消毒,他们也会用完剩余的消毒剂。
分析
直接模拟即可。
code
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=105;
int n,m,ans;
int h[N];
int main ()
{
cin>>n>>m;
for(int i=1;i<=n;i++)
{
cin>>h[i];
m-=h[i];
if(m>=0) ans++;
else m=0;
}
cout<<ans;
return 0;
}B - Uppercase and Lowercase
翻译
给你一个由小写和大写英文字母组成的字符串 \(S\) 。 \(S\) 的长度是奇数。
如果 \(S\) 中大写字母的数量大于小写字母的数量,请将 \(S\) 中的所有小写字母转换为大写字母。
否则,将 \(S\) 中的所有大写字母转换为小写字母。
分析
依旧是模拟,先统计 \(S\) 中小写和大写字母的个数进行比较,再根据比较结果进行修改。
code
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=105;
string s;
int main ()
{
cin>>s;
int a=0,b=0;
for(int i=0;i<s.size();i++)
{
if(s[i]>='a'&&s[i]<='z') a++;
else if(s[i]>='A'&&s[i]<='Z') b++;
}
int st=0;
if(a>b) st=1;
for(int i=0;i<s.size();i++)
{
if(st)
{
if(s[i]>='A'&&s[i]<='Z') cout<<(char)(s[i]-'A'+'a');
else cout<<s[i];
}
else
{
if(s[i]>='a'&&s[i]<='z') cout<<(char)(s[i]-'a'+'A');
else cout<<s[i];
}
}
return 0;
}C - Sierpinski carpet
翻译
对于一个非负整数 \(K\) ,我们定义一个 \(K\) 级地毯如下:
- \(0\) 级地毯是由一个黑色单元格组成的 \(1 \times 1\) 网格。
- 对于 \(K>0\) 来说, \(K\) 级地毯是一个 \(3^K \times 3^K\) 网格。当这个网格被分成九个 \(3^{K-1} \times 3^{K-1}\) 块时:
- 中央区块完全由白色单元格组成。
- 其他八个区块是 \((K-1)\) 级地毯。
"#" 为黑色单元格,"." 为白色单元格。
给你一个非负整数 \(N\) 。
请按照指定格式打印 \(N\) 级地毯。

分析
根据题意,\(K\) 极地毯(\(K>1\))都是可以由第 \(K-1\) 极地毯拼成的。
可以选择递推或递归来构造。
值得一提的是,不能直接打表,\(K\) 极地毯出现在程序中的话文件大小就超过限制了。
下面是递推的做法。
code
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=5005;
int n;
char s[10][10]={{"###"},{"#.#"},{"###"}};
char a[N][N];
int main ()
{
cin>>n;
int m=1;
for(int i=0;i<3;i++)
for(int j=0;j<3;j++)
a[i][j]=s[i][j];
for(int t=1;t<=n;t++)
{
m*=3;
for(int i=0;i<m;i++)
{
for(int j=0;j<3;j++)
for(int k=0;k<m;k++)
a[i][k+j*m]=a[i][k];
}
for(int i=0;i<m;i++)
{
for(int k=0;k<m;k++) a[i+m][k]=a[i][k];
for(int k=0;k<m;k++) a[i+m][k+m]='.';
for(int k=0;k<m;k++) a[i+m][k+2*m]=a[i][k];
}
for(int i=0;i<m;i++)
{
for(int j=0;j<3;j++)
for(int k=0;k<m;k++)
a[i+2*m][k+j*m]=a[i][k];
}
}
for(int i=0;i<m;i++)
{
for(int j=0;j<m;j++) cout<<a[i][j];
cout<<"\n";
}
return 0;
}D - 88888888
翻译
对于正整数 \(N\) ,设 \(V_N\) 是由 \(N\) 恰好连接 \(N\) 次所组成的整数。
更确切地说,把 \(N\) 看作一个字符串,连接它的 \(N\) 份,并把结果看作一个整数,得到 \(V_N\) 。
例如, \(V_3=333\) 和 \(V_{10}=10101010101010101010\) 。
求 \(V_N\) 除以 \(998244353\) 的余数。
分析
这是比较毒瘤的一道题了。
对于 \(n\):
它总共有 \(k\) 位数字,设 \(m=10^k\),可以发现,两个 \(n\) 拼起来就是 \(n+n*m\)。
\[V_n=n+n \times m+n \times m^2 + n \times m^3 + \dotsb + n \times m^{n-1} \]
显然,它是一个等比数列。
根据等比数列求和公式可知:
\[V_n=n+n \times m+n \times m^2 + \dotsb + n \times m^{n-1}=\frac{n(m^n-1)}{m-1} \]
分子部分可以直接用快速幂求解,而分母则需要用到逆元,模数是质数,可以直接用费马小定理求逆元。
复杂度是 \(log(n)\) 级别的。
其中需要注意的是,\(m\) 是可以直接取模后计算的,但是 \(n\) 会出现在指数上,不能先取模。
在指数上的 \(n\) 要取模应该模以模数 \(mod\) 的欧拉函数,也就是 \(mod-1\)。
code
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int mod=998244353;
ll qpow(ll x,ll y)
{
ll ret=1ll;
while(y)
{
if(y&1) ret=(ret*x)%mod;
x=(x*x)%mod;
y>>=1;
}
return ret;
}
string s;
ll n,m=1;
int main ()
{
cin>>s;
int len=s.size();
for(int i=0;i<len;i++) n*=10,n+=s[i]-'0',m*=10,m%=mod;
m%=mod;
ll ans=n%mod;
ans=(ans%mod*(qpow(m,n%(mod-1))-1))%mod;
ans=(ans%mod*qpow(m-1,mod-2))%mod;
cout<<ans;
return 0;
}E - Reachability in Functional Graph
翻译
有一个有向图,图中有 \(N\) 个顶点,编号为 \(1\) 至 \(N\) ,有 \(N\) 条边。
每个顶点的出度为 \(1\) ,顶点 \(i\) 的边指向顶点 \(a_i\) 。
计算有多少对顶点 \((u, v)\) 使得顶点 \(v\) 可以从顶点 \(u\) 出发到达。
这里,如果存在长度为 \(K+1\) 的顶点序列 \(w_0, w_1, \dots, w_K\) 且满足以下条件,则顶点 \(v\) 可以从顶点 \(u\) 到达。其中,如果 \(u = v\) 总是可达的。
- \(w_0 = u\) .
- \(w_K = v\) .
- 每个 \(0 \leq i \lt K\) 都有一条从顶点 \(w_i\) 到顶点 \(w_{i+1}\) 的边。
分析
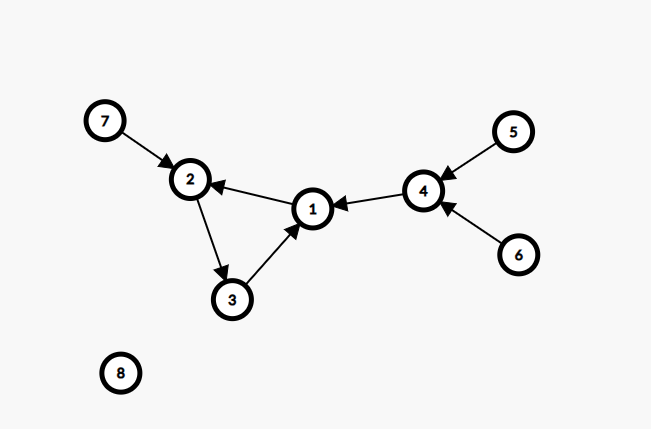
每个点出度都为 \(1\),共有 \(n\) 条边,可以发现这个图是一个基环树,而且是内向树。
从某一个节点出发的路径中,必定是包含了一个环的,或者说每条路径都是以环结束的,且第一个到达的环的节点就是环的初始点。
对于一个环来说,环中的每一个节点能到达的只有环中的点,每个点对答案的贡献就是环的节点数。
设 \(f[x]\) 为从点 \(x\) 出发能到达的节点数量。
例如 \(f[1]=3\),\(f[2]=3\),\(f[3]=3\)。
而在环外部的点,它必然能且只能到达一个环。从环的起始点开始往回走,依次统计节点贡献,每次加上自己。
例如 \(f[4]=f[1]+1\),\(f[5]=f[4]+1\)。
也就是说,首先要找到环,将环内部节点的 \(f\) 初始化为环的节点数。再进行统计,用记忆化搜索或者拓扑排序都是可以的。
因为一条路径必然以环结尾,可以选一条路一直走下去,沿途标记路径上的节点。碰到已经标记了的节点时,判断是不是当前路径的标记。如果不是,说明这条路结尾的环已经被处理过了;如果是,说明找到了环的初始点,此时需要再绕着环走一圈,统计环的节点数,再走一圈,将环初始化。
最后记忆化搜索,进行统计。
code
cpp
#include <bits/stdc++.h>
using namespace std;
const int N=2e5+5;
typedef long long ll;
int n;
int a[N],f[N];
int vis[N];
int dfs(int u)
{
if(f[u]) return f[u];
return f[u]=dfs(a[u])+1;
}
int main ()
{
cin>>n;
for(int i=1;i<=n;i++) cin>>a[i];
for(int i=1;i<=n;i++)
{
if(vis[i]) continue;
int u=i;
while(1)
{
if(vis[u])
{
if(vis[u]==i)
{
int v=a[u],cnt=1;
while(v!=u)
{
cnt++;
v=a[v];
}
f[u]=cnt;
v=a[u];
while(v!=u)
{
f[v]=cnt;
v=a[v];
}
}
break;
}
vis[u]=i;
u=a[u];
}
}
ll ans=0;
for(int i=1;i<=n;i++) ans+=dfs(i);
cout<<ans;
return 0;
}F - Two Sequence Queries
翻译
给你长度为 \(N\) 的序列 \(A=(A_1,A_2,\ldots,A_N)\) 和 \(B=(B_1,B_2,\ldots,B_N)\)
您还得到了 \(Q\) 个查询,需要按顺序处理。
查询有三种类型:
1 l r x: 将 \(A_l, A_{l+1}, \ldots, A_r\) 中的每一个元素加上 \(x\)。2 l r x: 将 \(B_l, B_{l+1}, \ldots, B_r\) 中的每一个元素加上 \(x\)。3 l r: 输出 \(\displaystyle\sum_{i=l}^r (A_i\times B_i) \mod 998244353\)。
分析
一道明显的线段树,需要维护两个数组,处理两个懒标记。
需要维护的元素是:\(A\) 数组的和 \(x\),\(B\) 数组的和 \(y\),还有 \(v=\displaystyle\sum_{i=l}^r (A_i\times B_i)\),其实都是和。
-
当 \(A\) 中每个元素加上 \(k\),\(x\) 就要加上 \(k \times len\),\(len\) 为区间长度。\(y\) 不会被改变,而 \(v\) 改变后的 \(v'\):
\[v'=\displaystyle\sum_{i=l}^r (A_i+k)\times B_i=\displaystyle\sum_{i=l}^r A_i\times B_i+\displaystyle\sum_{i=l}^r k\times B_i=v+y \times k \]
-
当 \(B\) 中每个元素加上 \(k\),同理,\(y'=y+k \times len\)。\(x\) 不变。
\[v'=v+x \times k \]
code
cpp
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=2e5+5,mod=998244353;
int n,q;
ll v1[N],v2[N];
struct node
{
int l,r;
ll x,y;
ll t1,t2;
ll v;
}a[N<<2];
#define L a[u].l
#define R a[u].r
#define lc (u<<1)
#define rc (u<<1|1)
#define mid (L+R>>1)
void pushup(int u)
{
a[u].x=(a[lc].x+a[rc].x)%mod;
a[u].y=(a[lc].y+a[rc].y)%mod;
a[u].v=(a[lc].v+a[rc].v)%mod;
}
void make(int u,ll t1,ll t2)
{
if(t1)
{
t1%=mod;
a[u].x=(a[u].x+(t1%mod*(R-L+1))%mod)%mod;
a[u].v=(a[u].v+(a[u].y*t1%mod))%mod;
}
if(t2)
{
t2%=mod;
a[u].y=(a[u].y+(t2%mod*(R-L+1))%mod)%mod;
a[u].v=(a[u].v+(a[u].x*t2%mod))%mod;
}
a[u].t1+=t1,a[u].t2+=t2;
a[u].t1%=mod,a[u].t2%=mod;
}
void pushdown(int u)
{
make(lc,a[u].t1,a[u].t2);
make(rc,a[u].t1,a[u].t2);
a[u].t1=a[u].t2=0;
}
void build(int u,int l,int r)
{
L=l,R=r;
if(l==r) a[u].x=v1[l]%mod,a[u].y=v2[l]%mod,a[u].v=((v1[l]%mod)*(v2[l]%mod))%mod;
else
{
build(lc,l,mid);
build(rc,mid+1,r);
pushup(u);
}
}
void update1(int u,int l,int r,int x)
{
if(l<=L&&R<=r) make(u,x,0);
else
{
pushdown(u);
if(mid>=l) update1(lc,l,r,x);
if(mid<r) update1(rc,l,r,x);
pushup(u);
}
}
void update2(int u,int l,int r,int x)
{
if(l<=L&&R<=r) make(u,0,x);
else
{
pushdown(u);
if(mid>=l) update2(lc,l,r,x);
if(mid<r) update2(rc,l,r,x);
pushup(u);
}
}
ll query(int u,int l,int r)
{
if(l<=L&&R<=r) return a[u].v%mod;
else
{
pushdown(u);
ll ret=0;
if(mid>=l) ret+=query(lc,l,r);
if(mid<r) ret+=query(rc,l,r);
return ret%mod;
}
}
void dfs(int u)
{
cout<<L<<" "<<R<<"\n";
cout<<a[u].x<<" "<<a[u].y<<" "<<a[u].v<<"\n";
cout<<a[u].t1<<" "<<a[u].t2<<"\n";
cout<<"___________________\n";
if(L==R) return ;
dfs(lc),dfs(rc);
}
int main ()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
cin>>n>>q;
for(int i=1;i<=n;i++) cin>>v1[i];
for(int i=1;i<=n;i++) cin>>v2[i];
build(1,1,n);
int op,l,r,x;
while(q--)
{
// dfs(1);
cin>>op>>l>>r;
if(op==1)
{
cin>>x;
update1(1,l,r,x%mod);
}
else if(op==2)
{
cin>>x;
update2(1,l,r,x%mod);
}
else cout<<query(1,l,r)<<"\n";
}
return 0;
}