一、说明
串扰应该算比较常见的信号完整性问题了,一般是指由于走线较近,传输信号时在临线上产生耦合噪声的现象。串扰的原因是由于电场和磁场的耦合,我们经常用耦合电容和耦合电感模型进行问题分析。
本文是基于被攻击线阻抗匹配的情形下计算的,没有考虑反射问题。
二、电容耦合
1.原因
当一根走线传输电压变换的信号时,周围电场则随之变化,导致相邻走线产生感应电流,引起噪声。这种情况我们常用电容耦合来分析。如下图,两根相邻走线是否就是平板电容呢?
我们提炼出电容耦合的模型:
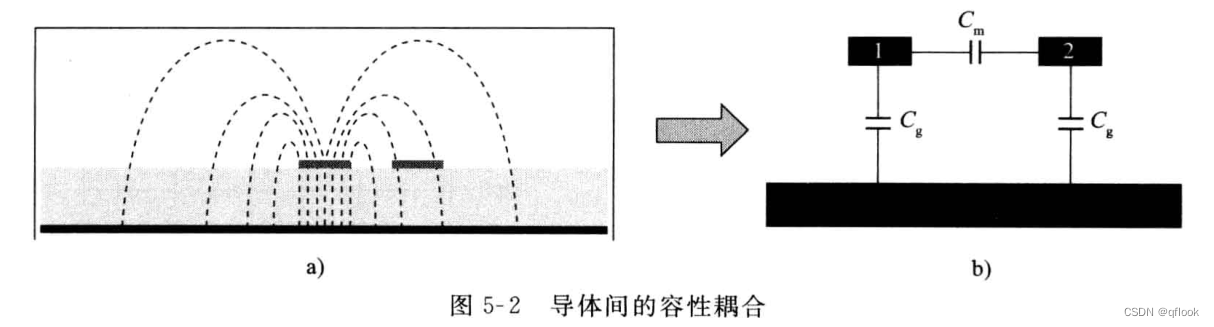
上图中Cm就是耦合电容,Cg就是对参考面的寄生电容。想象一下,Cg是不是也是对参考面的耦合电容?这里暂不展开了,大家可以考虑一下。
2.计算
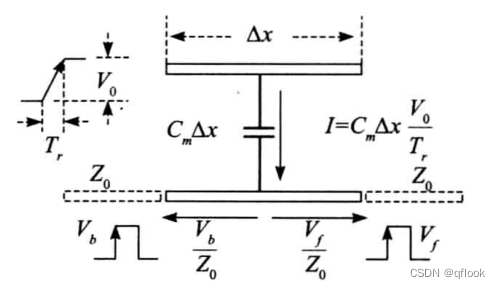
为了具体计算容性耦合的大小,这里采样的微分的概念,如下图:
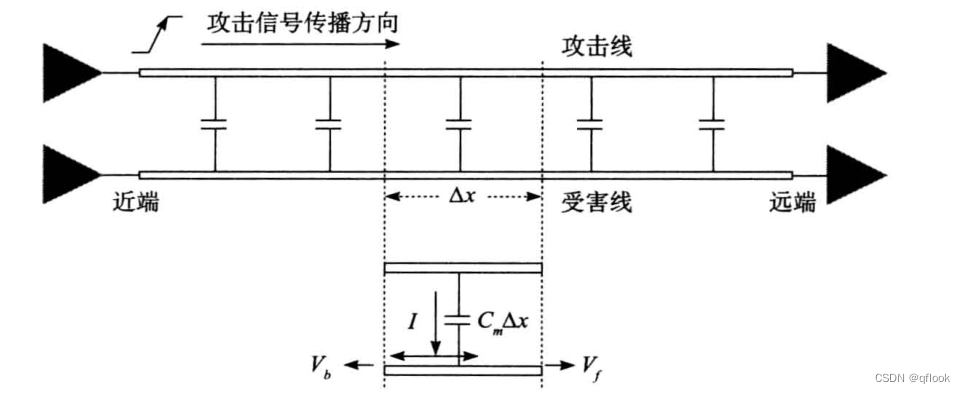
也就是说把信号线拆分成特别短的一小块$$\varDelta$$x,对于变化的电压,感应电流I则有:
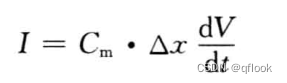
令近端串扰电压为Vb,远端串扰电压为Vf(近端串扰在干扰的后方,远端串扰在前方,因此命令为b和f)。则有,
Ib+If=Vb/Z0+Vf/Zf=I
同时又由于近、远端传输线特征阻抗都是Z0,则电流是平均分配的,也就是:
Ib=If
攻击信号电压幅度为V0,信号上升时间为Tr,则电压相对时间的微分就等于V0/Tr:
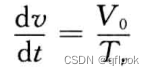
整理计算公式:
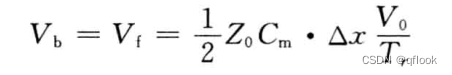
假如耦合传输线长度为L,则远端串扰总大小为:
VF=0.5*Z0*Cm*L*V0/Tr
近端串扰总大小呢,VB就不一定等于VF了,因为VB是有饱和的,也就是随着耦合传输线长度增大,VB是有上限的。原因是随着信号的传输,较远信号又叠加到近端串扰时,较近信号的影响已经过去,不能再叠加了。那最大是多少呢?就是上升时间Tr/2,攻击线上占用Tr/2时间,受害线近端串扰传输占用Tr/2。因此VB最大值为:
VB=0.5*Z0*Cm*Tr/2*Vp*V0/Tr=0.25*Z0*Cm*V0*Vp
其中Vp是指信号传输速度。
我们知道电流I的计算公式为:
I=Q/T=CU/(L/V)=CL*L*U*V/L=CL*U*V
CL的单位长度电容,U是电压,V是信号传播速度;
同时,
I=U/Z
Z=$$\sqrt{L/C}$$
整理公式得,
V=1/(CL*Z)=1/$$\sqrt{L*C}$$
将速度V和阻抗Z代入到本文中,则
Z=$$\sqrt{L0/(Cg+Cm)}$$
Vp=1/$$\sqrt{L0*(Cg+Cm)}$$
整理公式得:
VB=0.25*Cm*V0/(Cg+Cm)=0.25*V0-0.25*Cg*V0/(Cg+Cm)
3.对策
从远、近端串扰公式中我们可以明确得知,远端串扰是随耦合线长度无限叠加的(显示中由于插损的存在不会无穷大),近端串扰是随耦合电容增大而变大,极限大小就是四分之一的V0。
综上,如要改善近端串扰的最大值,只能减小耦合电容,例如增大线间距。如近端串扰没达到最大值,则可以通过减小耦合性长度、增大信号上升时间和减小耦合电容来改善;如要改善远端串扰,则只能减小耦合线长度或者增大信号上升时间。