硕士毕业论文《基于磁纹理的磁化动力学研究》

前言

本文是博主的硕士毕业论文，应该也是"自旋电子学（微磁学）"博客专栏的最后一篇博客，该毕业论文预设排版的PDF版本见下载链接：https://download.csdn.net/download/qq_43572058/89447526。若该博客专栏对读者您的研究过程有一定的帮助，那么博主十分期待读者能在恰当的时机合理地引用以下文章：

Q. Yi, Z. Tang, D. Zhu, X. Xing, W. Zhang, and Y. Zhou, "Magnonic bandgap openings and in-gap propagating states in domain-wall waveguides induced by periodic modulations," Phys. Rev. B 109(18), 184401 (2024). (https://doi.org/10.1103/PhysRevB.109.184401)

Q. Yi, T. Han, J. Jiang, and X. Xing, "A spin-torque nano-oscillator based on interlayer-coupled meron--skyrmion pairs with a fixed orbit," J. Appl. Phys. 135(18), 183901 (2024). (https://doi.org/10.1063/5.0195197)

感谢您的引用！

Thank you for citing!

#######

本文链接：https://blog.csdn.net/qq_43572058/article/details/138074540

CSDN@搬砖工人_0803号

#######

前言
摘要
[第一章绪论](#第一章绪论)
- [1.1 磁性起源和磁性材料](#1.1 磁性起源和磁性材料)
- [1.2 磁畴壁波导](#1.2 磁畴壁波导)
- [1.3 磁振子晶体](#1.3 磁振子晶体)
- [1.4 磁斯格明子](#1.4 磁斯格明子)
- [1.5 自旋转矩纳米振荡器](#1.5 自旋转矩纳米振荡器)
[第二章微磁学理论基础](#第二章微磁学理论基础)
- [2.1 静态微磁学](#2.1 静态微磁学)
- [2.2 动态微磁学](#2.2 动态微磁学)
- [2.3 微磁学模拟软件](#2.3 微磁学模拟软件)
[第三章磁畴壁波导的能带调控](#第三章磁畴壁波导的能带调控)
- [3.1 微磁模型和磁化构型](#3.1 微磁模型和磁化构型)
- [3.2 带隙打开的现象](#3.2 带隙打开的现象)
- [3.3 带隙打开的起源](#3.3 带隙打开的起源)
- [3.4 能带结构的影响因素](#3.4 能带结构的影响因素)
- - [3.4.1 几何周期参数对能带结构的影响](#3.4.1 几何周期参数对能带结构的影响)
  - [3.4.2 磁化构型对能带结构的影响](#3.4.2 磁化构型对能带结构的影响)
  - [3.4.3 弯曲磁振子晶体对能带结构的影响](#3.4.3 弯曲磁振子晶体对能带结构的影响)
  - [3.4.4 混合磁化构型对能带结构的影响](#3.4.4 混合磁化构型对能带结构的影响)
  - [3.4.5 间隔层厚度和Dzyaloshinskii-Moriya相互作用对能带结构的影响](#3.4.5 间隔层厚度和Dzyaloshinskii-Moriya相互作用对能带结构的影响)
[第四章具有固定轨道的自旋转矩纳米振荡器](#第四章具有固定轨道的自旋转矩纳米振荡器)
- [4.1 微磁模型和磁性参数](#4.1 微磁模型和磁性参数)
- [4.2 麦纫-斯格明子对的稳定机制](#4.2 麦纫-斯格明子对的稳定机制)
- [4.3 麦纫-斯格明子对绕固定轨道旋转运动](#4.3 麦纫-斯格明子对绕固定轨道旋转运动)
- [4.4 几何参数和磁性参数对振荡器输出频率的影响](#4.4 几何参数和磁性参数对振荡器输出频率的影响)
- [4.5 Thiele方程分析麦纫-斯格明子对动力学](#4.5 Thiele方程分析麦纫-斯格明子对动力学)
- [4.6 多个麦纫-斯格明子对提升振荡器输出频率](#4.6 多个麦纫-斯格明子对提升振荡器输出频率)
- [4.7 弱无序性参数对麦纫-斯格明子对动力学的影响](#4.7 弱无序性参数对麦纫-斯格明子对动力学的影响)
[第五章结论与展望](#第五章结论与展望)
- [5.1 总结](#5.1 总结)
- [5.2 展望](#5.2 展望)
参考文献
攻读学位期间取得与学位论文相关的成果

摘要

为了应对传统CMOS器件面临的焦耳热和器件小型化等瓶颈问题，兼顾电子的电荷和自旋属性而设计出来的自旋电子器件有望提供相应的解决方案，比如基于自旋波的器件更容易规避焦耳热，基于磁斯格明子的器件更容易小型化。

在本文中，我们设计了一个array-on-film结构的磁振子晶体来调控磁畴壁波导的能带结构，该磁振子晶体的两个铁磁层由非磁性间隔层分隔开，并通过偶极相互作用耦合。下方的连续铁磁层中预设了一个条状畴壁以当作自旋波的传输通道，而上方的铁磁层作为调制模块则是由一系列等距排列的短磁条带组成的条带阵列，并且每个条带的磁化构型可以独立改变。我们的模拟结果表明，条带阵列的几何参数和磁化构型可以对畴壁波导的能带结构产生显著的影响，具体而言，条带阵列的磁化分布允许控制带隙的存在、位置和宽度。有趣的是，凭借偶极耦合的波导和条带阵列存在的共振增强，在带隙内满足模式匹配的自旋波会转变为传播态，于是在带隙中出现了允带。我们的模拟研究展示了一种利用偶极耦合的铁磁双层结构来调控畴壁波导能带结构的方法，并期望在未来的磁振子电路中展现出应用潜力。

此外，为了解决基于磁斯格明子的自旋转矩纳米振荡器（Spin-torque nano-oscillators，STNOs）存在的一些缺点，例如启动时间长，变化的斯格明子旋转轨道等关键问题，我们实现了一种基于层间耦合的麦纫-斯格明子对（Meron-skyrmion pair，MS pair）且具有固定旋转轨道的STNO。研究表明即便存在弱无序性材料参数的情况下，MS pair在较宽的驱动电流范围内也具有固定的旋转轨道，并且该STNO的输出频率范围远高于典型的基于斯格明子的STNO。此外，通过在单个STNO中引入多个MS pair，可以进一步提高其输出频率。我们的结果展示了层间耦合MS pair的非平凡动力学，为基础自旋电子器件的设计和优化提供了范例。

关键词：磁纹理；磁振子晶体；自旋转矩纳米振荡器；磁化动力学；微磁学模拟

第一章绪论

随着近年来云计算和人工智能的高速发展，在海量的信息数据面前，处理器运算速度和存储器存储密度之间发展不平衡的矛盾日益增长，这促使着人们对磁学这门古老的学科进行更深入的探索，以期望实现将磁性材料的非易失性存储功能与高速数据处理能力相结合的新型技术，并逐渐演变成了一个新兴的研究领域------自旋电子学[1]。得益于磁性材料中共存的多种微观相互作用，这些相互作用会遵从能量最小化原理彼此竞争和互相妥协，导致磁体系中出现各种稳定的磁矩排列方式，从而自发形成丰富多样的磁纹理，比如磁畴壁、麦纫、斯格明子等等。巧妙地组合不同的磁纹理并合理地利用它们之间微妙的相互作用，不仅可以解决传统器件面临的一些难题，还能提供一些额外的新兴功能和应用场景。

回溯至上世纪80年代末，自德国的Peter Grünberg和法国的Albert Fert等科学家发现了磁性多层膜的磁电阻会因铁磁层内磁矩的排列方式而显著变化[2,3]，即巨磁电阻效应（Giant magnetoresistive effect，GMR），研究人员开始愈发关注电子的自旋属性，并探索出了利用铁磁层的磁化方向来调控电子输运特性的技术，从而广泛应用于硬盘的读出磁头以及磁随机存储器（Magnetic random access memory，MRAM）等器件[4,5]。由两铁磁层和中间的非磁性金属间隔层就构成了一个典型的自旋阀，当电流中的电子通过磁矩反平行排列的两铁磁层时，会受到较大的散射作用，此时的磁电阻最大，反之，平行排列时的磁电阻最小。将自旋阀中间的非磁性金属层替换为非磁性绝缘层就构成了一个典型的磁隧道结（Magnetic tunnel junction，MTJ）[6]，起源于量子隧穿效应的隧道电流同样依赖两铁磁层的磁矩排列方式，若两铁磁层的磁矩是反平行排列的，则隧道电流最小，为高阻态，反之，若磁矩是平行排列的，则隧道电流最大，为低阻态。

另一方面，Slonczewski和Berger等人于1996年理论提出了自旋转移矩（Spin-transfer torque，STT）效应[7,8]，即利用电子输运来调控磁化方向。垂直于铁磁薄膜表面的自旋极化电流（Current-perpendicular-to-plane，CPP）通过铁磁层时，自旋极化电子与局域磁矩之间发生自旋角动量转移，导致铁磁层内的磁矩受到Slonczewski类型转矩的作用而发生进动或翻转。若极化电流是平行于铁磁薄膜表面注入（Current-in-plane，CIP），则磁矩会受到Zhang-Li类型转矩的作用[9]，而极化电流会被逐渐极化到与磁化方向平行，其在空间上的变化正比于磁化方向的变化。实际上，对于重金属/铁磁双层组成的异质结来说，可以在重金属层中注入电流，利用其自旋轨道耦合导致的自旋霍尔效应（Spin Hall effect，SHE），使自旋相反的电子在重金属层两边分别积累，于是生成的纯自旋流便流入紧邻铁磁层内，并对其内部的磁矩施加自旋轨道矩（Spin-orbit torque，SOT）[10,11]。相较于STT，SOT避免了在铁磁层中产生焦耳热，有效降低了能源损耗。

1.1 磁性起源和磁性材料

万物皆有磁性，磁性作为物质的基本属性之一，其主要源于电子内禀的自旋诱导的自旋磁矩和电子围绕原子核做轨道运动诱导的轨道磁矩。人们通常按照物质的磁化强度 M 对外加磁场 H 的响应将之分为抗磁性，顺磁性，铁磁性，反铁磁性等材料[12]。

抗磁材料在外加磁场下会产生反向的磁化强度，即磁化率 χ = M H \chi=\frac{\mathbf{M}}{\mathbf{H}} χ=HM 为负值。顺磁材料无规的磁矩在外加磁场下会有指向磁场的趋势，从而可能表现出微弱的磁性[12]，其磁化率为10^-6^ ~ 10^-2^。铁磁材料的磁化率为10^-1^ ~ 10^5^，它们内部的相邻磁矩倾向于平行排列，如图1-1（a）所示，这些有序磁矩局限在磁畴区域内。在零磁场的情况下，许多磁化方向不同的磁畴可能相互抵消，从而导致铁磁材料宏观上不显示磁性，然而通常只需要一个很小的磁场便能将其磁化到饱和状态。铁磁材料存在居里温度，当高于居里温度时会转变为顺磁性材料[12]。

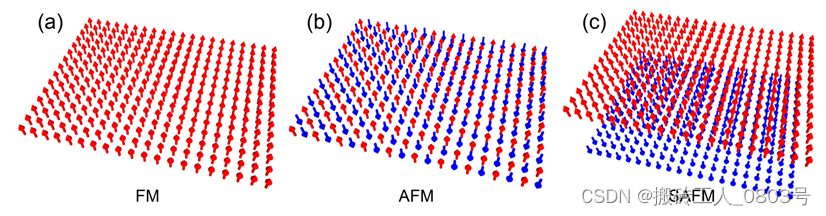
(a) 相邻磁矩倾向于平行排列的铁磁材料，(b) 相邻磁矩倾向于反平行排列的反铁磁材料，(c) 人工合成反铁磁的上、下铁磁层磁矩倾向于反平行排列

图1-1 磁性材料中磁矩排列的示意图

天然反铁磁材料的磁化率为10^-5^ ~ 10^-3^，它们内部的相邻磁矩倾向于反平行排列，如图1-1（b）所示，这导致了相邻磁矩辐射的偶极场互相抵消，于是反铁磁的宏观净磁矩为零从而对外不显示磁性。反铁磁材料存在奈尔温度，它们在高于奈尔温度时会转变为顺磁性材料[12]。

此外，相比于天然反铁磁，人工合成反铁磁（Synthetic antiferromagnets，SAFM）的研究前景更为广阔[13,14]。典型的合成反铁磁由两铁磁层和中间的非磁性间隔层构成，两铁磁层之间通过RKKY（Ruderman--Kittel--Kasuya--Yosida）层间交换相互作用实现反铁磁耦合，即两铁磁层的磁化方向相反，如图1-1（c）所示。通常合成反铁磁的层间交换耦合强度比天然反铁磁的直接交换或超交换耦合更弱，这使得合成反铁磁的反铁磁序比天然反铁磁更容易操纵。此外，合成反铁磁的层间交换耦合强度是随着间隔层的厚度增加而振荡变化的，即两铁磁层会在反铁磁耦合和铁磁耦合之间交替变换。但对于间隔层非常厚的情况，层间交换耦合显然被抑制[13]。

1.2 磁畴壁波导

自旋波是磁性材料中局部微扰造成磁矩的非一致进动并以波的形式进行传播[15]，其准粒子称为磁振子（Magnons）。自旋波既可以存在于磁性金属也可以存在于磁性绝缘体中，其特征频率范围包含GHz到THz，波长可短至纳米数量级，且在传播过程中不涉及电荷转移进而可以规避焦耳热[16]。由于自旋波也具有振幅、频率、相位等波的特征，若借助自旋波作为信息载体去执行信息传输或逻辑计算，那么设计出来的自旋波器件将拥有极小的尺寸和极低的功耗[16]。

在均匀磁化的磁畴波导中传播的体模式自旋波早已被广泛研究，提出的各种自旋波器件如移相器[17--21]，分波器[22,23]，耦合器[24,25]，放大器[26,27]和其他逻辑门器件，具有结构简单、调控手段多样化等优点。移相器的经典设计思路是在波导中引入局域的非均匀势场，从而使自旋波的相位发生改变[17]，如图1.2（a）所示。

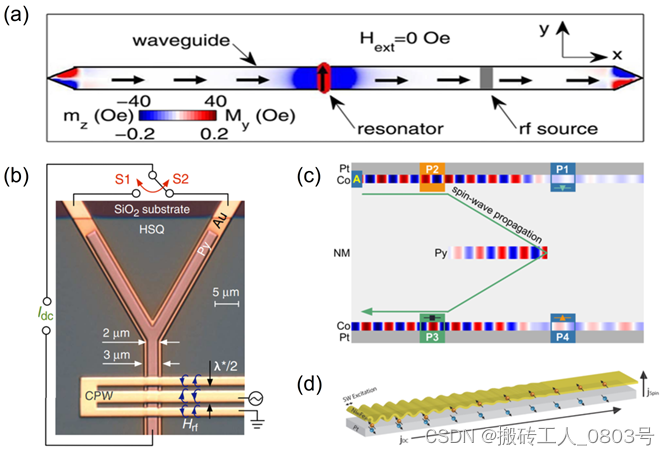
(a) 自旋波移相器[17]，(b) 自旋波分波器[22]，(c) 自旋波耦合器[25]，(d) 自旋波放大器[27]

图1-2 基于自旋波的功能器件

一种典型的自旋波分波器的设计如图1-2（b）所示，其通过电流诱导的奥斯特磁场来改变局域的磁化分布，从而可以操纵自旋波的传播路径[22]。耦合器通常是利用波导中自旋波辐射的动态杂散场在其他波导中诱导出自旋波，从而实现自旋波在不同波导之间转移的功能[25]，如图1-2（c）所示。放大器则是借助极化电流对磁矩施加的STT或者SOT去补偿自旋波传播过程中的阻尼耗散[27]，如图1-2（d）所示。

自2015年开始，有研究人员理论提出将磁畴壁作为自旋波传输的通道，并设计出基于畴壁波导的逻辑门和二极管器件[28--30]。如图1-3（a）所示，在垂直磁化的条带中间预设一个条状畴壁，样品中心的黄色区域表示用于激发自旋波的条带天线。该条状畴壁会引入一个宽度方向上的势阱，因此若激发的自旋波频率低于体模式自旋波的截止频率，则仅会在畴壁内激发出自旋波并束缚在畴壁内传播，表现出优秀的1D传播特征。若磁体系不存在界面Dzyaloshinskii-Moriya相互作用（DMI），则该条状畴壁为Bloch畴壁，于是束缚在其内部的自旋波具有互易性的传播特性，体现为红色的色散曲线是关于中心对称的。若磁体系存在界面DMI，则条状畴壁为Néel畴壁，内部的束缚态自旋波具有非互易性的传播特性，体现为蓝色的非对称色散曲线。此外，对比黑色的色散曲线，即磁畴中的体模式自旋波，束缚态自旋波拥有接近于零的截止频率和更高的群速度等优点[28]。

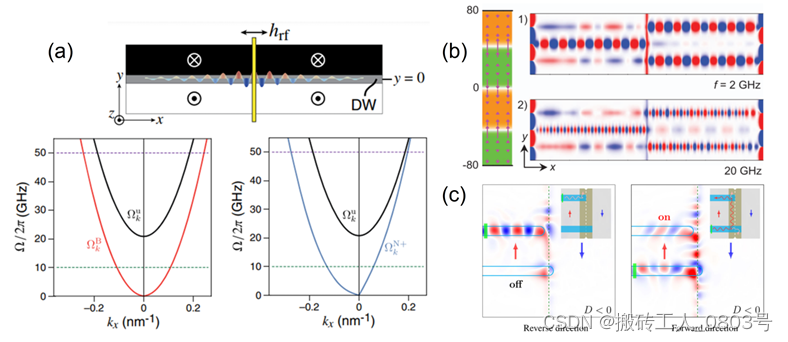
(a) 磁畴壁波导和色散关系[28]，(b) Néel畴壁波导并行工作[29]，(c) 自旋波二极管[30]

图1-3 磁畴壁波导及其应用

将磁畴壁用作波导的另一个优点是可以在单个条带内实现自旋波的多通道并行传输[29]，如图1-3（b）所示。将四个磁畴分隔开的三个条状Néel畴壁的磁化方向是两两相反的，并且它们作为自旋波的传输通道具有一定的独立性，即在一个Néel畴壁波导内的束缚态自旋波对其余两个畴壁波导内的束缚态自旋波几乎没有影响。图1-3（c）展示了一种基于畴壁波导的双端器件，其功能是只能在特定的一个端口注入自旋波，并在另一端口检测输出，即表现出自旋波二极管单向导通的特征。该器件中的自旋波传播路径依赖磁体的手性，将DMI符号反转即可实现可重构的自旋波二极管[30]。

除了理论研究，也有研究人员在后续的实验证实了将纳米尺寸的磁畴壁作为波导的可行性[31--34]。研究发现较低频率的自旋波只在磁畴壁内部传播，而不会泄露到外面的磁畴区域中，但较高频率的自旋波则会同时在磁畴壁和磁畴中传播。此外，还可以通过磁场等手段调节畴壁波导的位置，进而实现可重构的自旋波传输通道。

由于畴壁波导具有上述优点，再加上对样品边缘粗糙和缺陷不敏感，相比于已经被广泛研究的传统波导来说，对基于畴壁波导的新型器件和应用场景进行更深入、更广泛的探索是非常有必要的，这将提高自旋波器件对比CMOS器件在信号传输和信息处理方面的潜在优势[35]。比如怎样生成畴壁波导[36]，如何探测畴壁波导内的自旋波[37]，怎样放大或衰减束缚态自旋波的振幅[38]，如何调节畴壁波导的截止频率[39]。

1.3 磁振子晶体

磁振子晶体（Magnonic crystals，MCs）是光子晶体的磁性对应物，研究人员在近些年来对其进行了广泛而深入的研究。磁振子晶体是一种具有周期性结构的磁性材料，它的能带结构由一系列允带和禁带（或带隙）组成，分别允许和禁止自旋波在磁振子晶体中传播，其能带结构可以通过改变周期参数来调控。无论是薄膜还是块体磁振子晶体，都可以按照其周期性结构可扩展的维度将之分为：仅在一个方向上存在周期的1D磁振子晶体；在两个方向上存在周期的2D磁振子晶体；以及在三个方向上都存在周期的3D磁振子晶体[40]，如图1-4（a）所示。

磁振子晶体带隙的起源通常包含多个原因，对于已经被广泛研究的1D磁振子来说，其带隙形成的原因之一是由于周期结构引入了周期势场，导致在布里渊区边界满足布拉格反射条件的入射自旋波和反射自旋波叠加在一起形成了驻波，从而阻止了自旋波穿过周期势场并在能带中形成了带隙[16]，如图1-4（b）所示。类比于电子在一维晶格中运动[41]，实空间中磁振子晶体的周期结构体现为倒空间中色散曲线的平移不变性，按图1-4（c）所示，在非零周期势场存在的情况下，将色散曲线沿着波矢轴的布里渊区边界进行折叠，这些波矢交叉点即满足布拉格反射条件，于是可以通过观察色散曲线是否在带隙处折叠交叉从而确定带隙形成的原因。

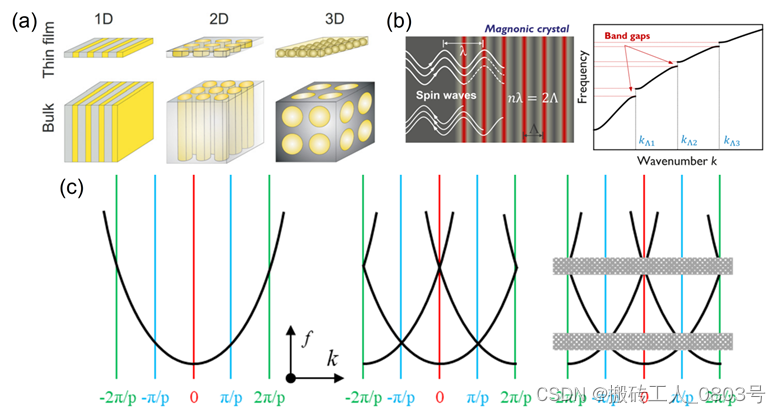
(a) 磁振子晶体的分类[40]，(b) 布拉格反射机制[16]，(c) 色散曲线折叠交叉并打开带隙[41]

图1-4 磁振子晶体及其带隙起源

磁振子晶体能够实现多种自旋波器件的功能，如滤波、延迟线、模式衰减和相位调制等等[42]，虽然有一些功能仍然处于早期的理论发展阶段，但大多数功能已经在其他类型的人造晶体中得到了证实。和光子晶体通过改变介电材料的周期参数来调控能带结构类似，磁振子晶体的能带调控也依赖于周期参数的变化[40]。在磁振子晶体中引入静态的、"硬"的周期结构，如样品的材料、几何形状等取决于复杂的纳米制造过程，一旦周期结构制造完成，那么磁振子晶体的能带结构就固定不变了[43--49]。相反，引入可重构的、"软"的周期结构，如周期性排列在磁振子晶体中的磁畴壁、磁斯格明子、磁霍普夫子等磁纹理，由于它们可以被磁场或电流等外力动态调控，为周期性调控提供了额外的自由度，因此可以制造出具有可编程能带结构的磁振子晶体[50--59]。

对磁振子晶体的"硬"周期进行调控的一种经典范例是G. Gubbiotti等人利用偶极耦合的坡莫合金纳米条带阵列实现的1D磁振子晶体[44]，如图1-5（a）所示。与在均匀磁化的连续条带中传播的自旋波不同，偶极耦合的条带阵列中存在几种离散的集体模式自旋波在条带之间传播，表现为能带中允带的形成。还有一种经典的"硬"周期调控方法是Ki-Suk Lee等人提出的通过修饰波导的两侧边来调控能带结构[45]，如图1-5（b）所示。这种1D磁振子晶体的一些带隙起源于周期势场以及布拉格反射的作用，另一些带隙则是起源于高阶散射模式和低阶模式之间反交叉的色散曲线。

近年来人们逐渐关注磁振子晶体"软"周期的调控，以期望实现可编程的能带结构。Andrii V. Chumak等人在磁性绝缘体钇铁石榴石（YIG）波导上方生成金属的曲折结构[50]，如图1-5（c）所示。当往曲折结构通入电流后，其诱导的周期性奥斯特磁场会辐射到下方的波导中，于是波导中形成的周期势场会导致能带中带隙的打开。然而一旦撤去电流，带隙则会关闭。Fusheng Ma等人理论提出将斯格明子阵列放置在均匀磁化的条带波导中，从而使波导的磁化分布受到周期调控，导致在能带中打开了多个带隙[56]，如图1-5（d）所示。此外，可以通过施加磁场、极化电流等手段来动态调节斯格明子阵列的周期参数，进而改变带隙的位置、宽度和数量等特征。

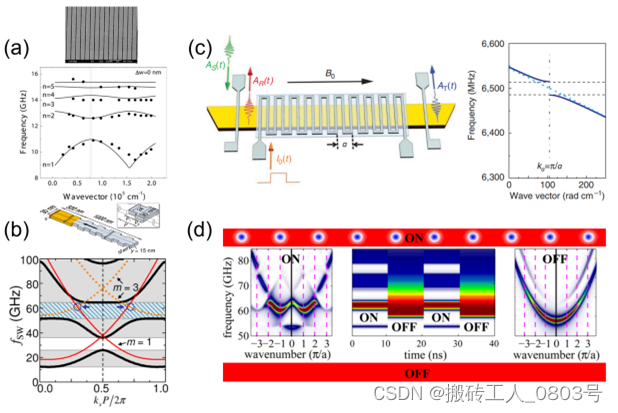
(a) 偶极耦合的磁条带阵列构成的磁振子晶体[44]，(b) 边缘调控的磁振子晶体[45]，(c) 受电流的奥斯特磁场控制的动态磁振子晶体[50]，(d) 斯格明子阵列构成的可重构磁振子晶体[56]

图1-5 磁振子晶体的实现

迄今为止，几乎所有报道的磁振子晶体都是基于传统的磁畴波导，但是与畴壁波导兼容的磁振子晶体尚待寻找。在本文中，我们设计了一个偶极耦合的array-on-film结构，通过改变磁体系的磁化构型和几何固有周期参数来实现对畴壁波导的能带结构进行调控。

1.4 磁斯格明子

磁斯格明子（Magnetic skyrmions）是一种具有拓扑保护的粒子状的磁纹理，由于其具有稳定性高、较小的尺寸和较小的驱动电流等优点，基于斯格明子的多功能逻辑器件和高密度信息存储器近年来受到广泛的关注[60--63]。自2009年S.Mühlbauer等人在手性磁体MnSi中首次观察到斯格明子以后[64]，后续越来越多的实验证据确认了斯格明子可以在手性磁体、磁性薄膜、Heusler化合物和阻挫磁体等多种材料体系中稳定存在[60--63]。现阶段已经确定了存在几种机制来确保斯格明子的稳定[63]：（1）Dzyaloshinskii-Moriya 相互作用（DMI）；（2）经典的长程磁偶极相互作用；（3）阻挫型交换相互作用；（4）四自旋交换相互作用。

DMI会使磁体系中的紧邻磁矩倾向于垂直排列，是一种反对称的交换相互作用，存在DMI的磁体即为手性磁体。若磁体是中心反演对称性破缺如FeGe、MnSi等块体材料，则存在体型（bulk）DMI。若磁体是界面对称破缺的磁性薄膜异质结如Pt/Co、Ir/Fe等，则存在界面型（interfacial）DMI。对于由DMI机制稳定的斯格明子来说，体型DMI倾向于形成Bloch型斯格明子，界面型DMI倾向于形成Néel型斯格明子。典型的Bloch斯格明子和Néel斯格明子的磁化分布如图1-6（a）和（b）所示，它们的中心磁化和背景磁化由一个闭合的环状畴壁分隔开，并根据畴壁的类型进行分类。沿Néel斯格明子的中心进行切片，即可观察到Néel畴壁内的磁矩呈现径向排列的特征，并可以进一步确定斯格明子的手性和极性，即若Néel畴壁内的磁矩从 -z 指向 +z 则为左手性，若斯格明子中心的磁化方向指向 -z 则极性为负。Bloch斯格明子实际上是一种拓扑电荷不等于0的特殊磁泡（Magnetic bubbles），从Bloch斯格明子的切片中可看到其畴壁内的磁矩呈现圆形排列的特征。此外，在合成反铁磁中，还可能存在反铁磁耦合的斯格明子对组成的双层斯格明子（Bilayer skyrmions）[65]，如图1-6（c）所示。

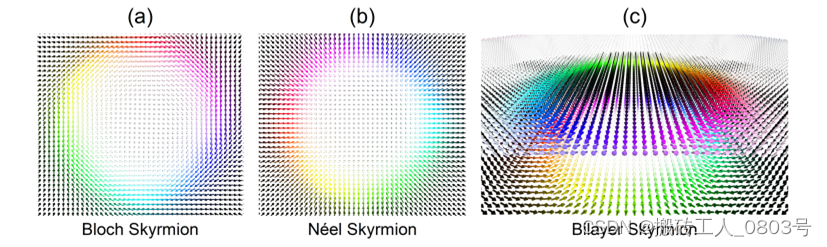
(a) Bloch型斯格明子，(b) Néel型斯格明子，(c) 合成反铁磁中的双层斯格明子

图1-6 斯格明子磁纹理

生成单个斯格明子的经典方法是在纳米受限结构处翻转其局域磁化，并利用电流扩大磁化翻转来诱导斯格明子成核。Junichi Iwasaki等人设计了包含缺口的磁性平板[66]，该平板缺口处的磁化主要受形状各向异性的影响而变得不均匀分布，如图1-7（a）所示。通过施加一个面内电流即可翻转缺口处的局域磁化，即首先生成了一个边缘麦纫[67--69]，接着电流驱动这个边缘麦纫演变为斯格明子。Yan Zhou等人设计了一种由两根宽度不同的条带连接成的纳米受限结构[70]，如图1-7（b）所示。当面内电流驱动畴壁对从较窄的条带进入较宽的条带时，前侧的畴壁同样是先转变成了一个边缘麦纫，接着便是从开放的畴壁对完全转化成斯格明子的闭合环状畴壁。该转化过程是可逆的，即通入反向的面内电流可实现从斯格明子的闭合环状畴壁到畴壁对的转化。Wanjun Jiang等人在实验上实现了利用条状磁畴生成斯格明子[71]，其转化机制如图1-7（c）所示。通过在和铁磁层CoFeB紧邻的重金属Ta层中注入面内电流，从而让诱导的自旋轨道矩推动条状磁畴前面的半圆形畴壁移动。当不断扩张的条状磁畴从窄条带进入宽条带时，在样品边缘诱导的力和自旋流诱导的力的合力作用下，条状磁畴就会转变成一个个的斯格明子，整个斯格明子的生成过程就类似于在日常生活中吹肥皂泡泡的过程。

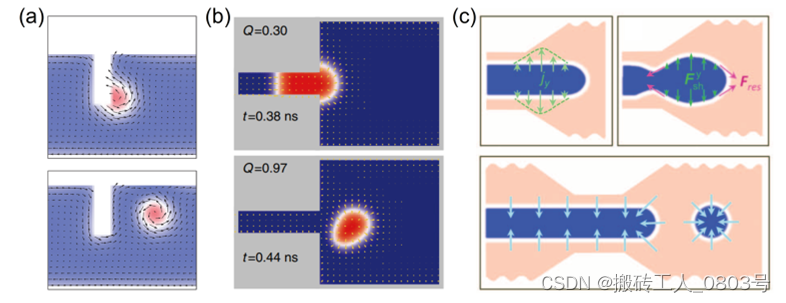
(a) 面内电流促使斯格明子在纳米受限结构的缺口处成核[66]，(b) 在窄条带和宽条带连接成的受限结构中生成斯格明子[70]，(c) 类似于吹肥皂泡泡将条状磁畴"吹"成斯格明子[71]

图1-7 斯格明子的成核

通过对磁纹理进行空间积分，可以得到一个描述其拓扑电荷 Q 的表达式[63]：
Q = 1 4 π ∬ m ⋅ ( ∂ m ∂ x × ∂ m ∂ y ) d x d y ( 1.1 ) Q=\frac{1}{4\pi}\iint{\mathbf{m}\cdot\left(\frac{\partial\mathbf{m}}{\partial{x}}\times\frac{\partial\mathbf{m}}{\partial{y}}\ \right)}{dx}{dy} (1.1) Q=4π1∬m⋅(∂x∂m×∂y∂m )dxdy(1.1) 其中 m = m (x , y ) 是归一化的磁化强度矢量场。斯格明子由于其整数的拓扑电荷因而具有拓扑保护特性，然而边缘麦纫具有分数拓扑电荷[67,68]，平凡畴壁的拓扑电荷为零。斯格明子的拓扑保护特性使它在面对诸如电流、外加磁场等常规的激励都能保持结构不被破坏，因此有研究人员提出根据斯格明子的存在与否来表示二进制的"1"和"0"，并用于设计新型赛道存储器[72]。如图1-8（a）所示，斯格明子在合适的电流密度下能绕过条带边缘处的缺陷，避免钉扎或湮灭在条带中。当使用电流驱动条带中的斯格明子队列时，斯格明子之间仍然能维持预设的间隔距离并保持同步移动，满足了赛道存储器所需的要求。

除了关注斯格明子的拓扑保护特性外，研究其独特的环状畴壁与自旋波的相互耦合也能打开新的研究视野。关于基于斯格明子的自旋波器件，除了上一节介绍的基于斯格明子的磁振子晶体外，Zhenyu Wang等人还在理论上提出利用斯格明子对自旋波的非线性散射现象来设计磁频率梳[73]。如图1-8（b）所示，微波磁场激发的一定振幅和频率的入射自旋波遇到斯格明子时，会与斯格明子的环状畴壁发生强烈的非线性相互作用，从而导致散射自旋波的频率谱中出现等间隔频率分布的峰值，其间隔频率为斯格明子呼吸模式的频率。

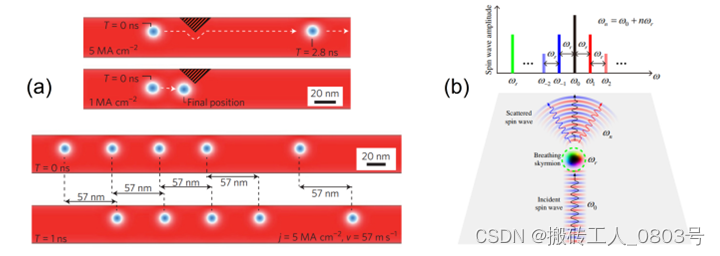
(a) 基于斯格明子的赛道存储器[72]，(b) 基于斯格明子的磁频率梳[73]

图1-8 基于斯格明子的功能器件

需要注意的是，由于自旋波携带着自旋角动量，所以在自旋波与斯格明子相互作用的过程中一般伴随着角动量的转移，即自旋波可以用来驱动斯格明子[73--81]，这可能对某些依赖斯格明子空间位置的自旋波器件有一定的影响，所以这些器件一般要求自旋波的振幅尽可能的小，用于确保斯格明子的位置基本不变[56,82]。

1.5 自旋转矩纳米振荡器

自旋转矩纳米振荡器（Spin-torque nano-oscillators，STNOs）是用于将输入的直流电流转化为微波信号的器件，这种器件不需要任何具有正增益的有源反馈电路来维持运行，并且具有高度非线性、频率可调、注入锁定和相互同步等特点，因此它们被认为是下一代自旋电子器件的关键所在[83]。对基于磁单畴[84--86]、磁涡旋[87--89]振荡器的研究有着悠久的历史，并已经发展出了成熟的理论且取得了丰富的实验结果，因此存在商业化的潜力。不过近年来，由于斯格明子在自旋电子学相关的研究中大放异彩，人们开始探索设计基于斯格明子的自旋转矩纳米振荡器，并在理论方面取得了长足的进步。

Senfu Zhang等人设计了一对点电极加经典的磁性三明治结构组成的振荡器，该三明治结构包含一个较厚的铁磁圆盘作为极化层，一个较薄的铁磁圆盘作为自由层，以及一个非磁性间隔层[90]，如图1-9（a）所示。他们首先通过点电极往自由层注入非常大的极化电流以用于生成斯格明子，接着减小电流以用于驱动斯格明子螺旋地离开圆盘中心并到达合适的圆周轨道，最后斯格明子在持续的极化电流作用下会沿着该轨道周期旋转。该振荡器的实际输出频率取决于斯格明子的旋转频率，虽然圆盘中单个斯格明子的旋转频率仅达到几百MHz，但是可以通过往圆盘中放置多个中心对称分布的斯格明子并让它们进行同步旋转，利用这种方式可以巧妙地将振荡器的实际输出频率提高到数GHz。

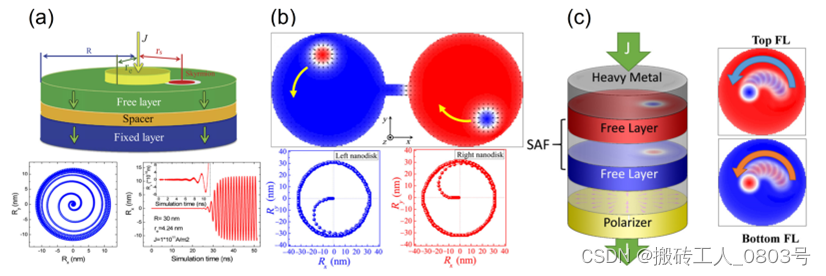
(a) 基于单层斯格明子的STNO[90]，(b) 哑铃形状的STNO[91]，(c) 基于双层斯格明子的STNO[92]

图1-9 基于斯格明子的自旋转矩纳米振荡器

Chendong Jin等人基于上述斯格明子振荡器的原理，巧妙地利用畴壁和斯格明子之间的排斥相互作用来让连接两圆盘的中间条带内的畴壁进行往复平移[91]。他们的研究表明该哑铃状振荡器对比原始模型拥有着更大的输出功率和更高的输出频率，并且可以利用该哑铃状振荡器构建更大规模的振荡器阵列，从而进一步提高实际输出功率。Sai Zhou等人将原始的基于单层斯格明子的振荡器扩展到合成反铁磁圆盘中的双层斯格明子，并通过微磁模拟和Thiele方程分析了点电流驱动双层斯格明子的旋转动力学[92]。他们的结果表明上下两层的斯格明子在极化方向相反的双层电流下会沿相反的方向旋转，当存在较强的层间交换相互作用时，斯格明子对的合成运动方向指向圆盘中心，即不能同步旋转运动。然而若是考虑单层的极化电流，则受该电流驱动的单层斯格明子会通过层间交换相互作用来拖拽另一层的斯格明子，最终实现双层斯格明子的同步旋转。此外，他们还发现阻尼系数和电流大小等因素对双层斯格明子稳定旋转时的轨道半径和旋转频率有较大的影响。

综上所述，目前报道的基于类似于斯格明子这种磁孤子的振荡器拥有着驱动电流小、输出频率的可调范围宽、多个斯格明子可以在一个振荡器中同步旋转等优点[90,93]。然而，在铁磁圆盘中的单个斯格明子的旋转频率通常较低，电流驱动的斯格明子从圆盘中心运动到稳定旋转轨道的启动时间较长。此外，斯格明子的旋转轨道半径还会随注入电流而变化，从而使基于磁电阻效应检测斯格明子的装置变得更加复杂，这些缺点限制了这类振荡器的实际应用。当然若是将铁磁圆盘替换为天然反铁磁或者合成反铁磁圆盘，则基于反铁磁斯格明子或斯格明子对的振荡器的输出频率将从本质上得到提高[92,94,95]。若是在纳米圆盘的环状区域通过刻蚀或者通过调节磁性参数来引入势阱，从而限制斯格明子的旋转轨道，则会显著缩小启动时间和简化斯格明子检测装置的设计[96--100]。然而利用当前的实验技术来精准修饰纳米圆盘中如此小的特定环状区域仍然是一个挑战，所以到目前为止，仍然缺乏一个能够同时解决上述问题的解决方案。在本文中我们设计了一个非对称的合成反铁磁圆盘，其中反铁磁耦合的麦纫和斯格明子对混合磁纹理能始终沿着圆盘边缘旋转并且拥有着极小的启动时间。

第二章微磁学理论基础

人们对现代磁学的研究尺度囊括了微观的原子层面到宏观的磁性块体，并针对不同的研究尺度发展出了相应的理论，以确保能准确描述相应的磁体系。

从理论物理的角度来看，使用量子力学理论模型对磁体系的描述是最准确的，然而考虑到其计算过程的复杂性随着磁体尺度呈指数增加，所以该理论模型通常仅用于分析低于纳米尺度的磁体系。当研究毫米以上的宏观磁体系时，一般不需要关心磁体内部的磁化分布，而是需要获取整个磁体表现出来的宏观性质，所以使用磁畴理论和磁性相变理论模型进行研究便足矣。然而当研究尺度介于纳米到微米量级时，使用微磁学理论模型不仅能准确描述磁体内部的磁化分布，还能简化理论计算的复杂程度。此外，借助便利的微磁学数值模拟还可以预测实验结果并以此提高研究效率。

微磁学使用半经典的连续性近似方法将微观层面的若干个原子的磁性等效为一个具有特定大小和方向的磁矩，于是单位体积中的所有磁矩就形成了一个连续的磁化强度矢量场[16]，即 M = M ( r , t ) = ∑ i u i δ V \mathbf{M}=\mathbf{M}(\mathbf{r},t)=\frac{\sum_{i}\mathbf{u}_i}{\delta V} M=M(r,t)=δV∑iui。磁化强度矢量场是空间和时间的函数，并被认为是可微的。该矢量场的模值即是饱和磁化强度 M ~s~，并被假设为不随时间变化，即有 M s = ∣ M ∣ = c o n s t M_s=\left|\mathbf{M}\right|=const Ms=∣M∣=const。此外，在研究中为了简化分析，也经常使用归一化的磁化强度矢量场 m = m ( r , t ) = M ( r , t ) M s \mathbf{m}=\mathbf{m}(\mathbf{r},t)=\frac{\mathbf{M}(\mathbf{r},t)}{M_s} m=m(r,t)=MsM(r,t)。

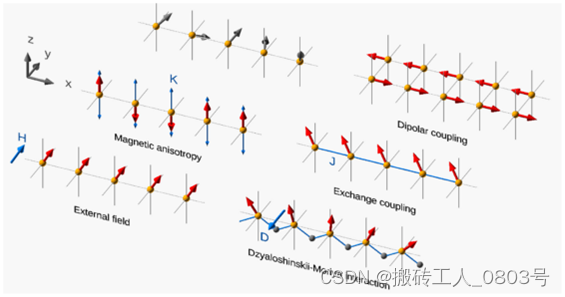
图2-1 磁矩在各种相互作用下的相应排列方式[35]

微磁学将磁体系中存在的多种微观相互作用等效为相应的有效磁场和磁性能量，比如外加磁场导致的塞曼能 E ~z~，交换相互作用导致的交换能 E ~ex~，偶极相互作用导致的退磁能 E ~dem~，磁晶各向异性导致的各项异性能 E ~a~，Dzyaloshinskii-Moriya相互作用（DMI）导致的DMI能 E ~DMI~。于是磁体系具有的总能量 E ~total~表示为： E t o t a l = E z + E e x + E d e m + E a + E D M I ( 2.1 ) E_{total}=E_z+E_{ex}+E_{dem}+E_a+E_{DMI} (2.1) Etotal=Ez+Eex+Edem+Ea+EDMI(2.1) 这些（标量值）能量会分配到整个磁体系中，即相应的（标量场）能量密度w 为： E = ∫ V w ( m ) d V E=\int_Vw(\mathbf{m})dV E=∫Vw(m)dV。磁体系中的磁矩在这些相互作用下会适当取向以满足能量最小化原理，如图2-1所示[35]。接下来将分别介绍这些磁性能量：
1. 塞曼能

外加磁场是调控磁体系最重要的手段之一，其形式可以为直流的偏置磁场，也可以为交流的时变磁场，磁体系处于外加磁场中获得的能量即称为塞曼能。塞曼能的能量密度表达式为：
w z = − u 0 M s m ⋅ H a p p ( 2.2 ) w_z=-u_0M_s\mathbf{m}\cdot\mathbf{H}_{app} (2.2) wz=−u0Msm⋅Happ(2.2)

显然，塞曼能是随着磁化强度与外加磁场 H ~app~ 的夹角而变化的。当磁化强度平行于外加磁场时，塞曼能最小。而当它们反平行时，塞曼能则最大。所以在外加磁场的作用下，磁化强度会倾向于平行外加磁场的方向来最小化塞曼能。
2. 交换能

微磁学考虑海森堡交换相互作用在连续近似下的能量密度为：
w e x = A m ⋅ ∇ 2 m = A [ ( ∇ m x ) 2 + ( ∇ m y ) 2 + ( ∇ m z ) 2 ] ( 2.3 ) w_{ex}=A\mathbf{m}\cdot\nabla^2\mathbf{m}=A[(\nabla m_x)^2+(\nabla m_y)^2+(\nabla m_z)^2] (2.3) wex=Am⋅∇2m=A[(∇mx)2+(∇my)2+(∇mz)2](2.3)

为了方便，也可将上式写为： w e x = A ( ∇ m ) 2 w_{ex}=A(\nabla\mathbf{m})^2 wex=A(∇m)2，其中 A 是磁性材料的交换系数，单位为 J/m。在微磁学模拟中，设置 A > 0 可以用于模拟铁磁材料，而设置 A < 0 则可以模拟天然反铁磁材料。显然，当 A > 0 时，磁体系中的紧邻磁矩平行排列时交换能最小，而当 A < 0 时，紧邻磁矩反平行排列时交换能最小。实际上，交换相互作用的作用范围是短程的，只有处于交换长度 l e x = 2 A ( μ 0 M s 2 ) l_{ex}=\sqrt{\frac{2A}{\left(\mu_0M_s^2\right)}} lex=(μ0Ms2)2A 内的磁矩才存在交换耦合。

此外，对于合成反铁磁来说，由间隔层物理分隔开的两铁磁层之间还存在层间交换相互作用，仅考虑其双线性界面交换系数项的能量密度表达式为：
w i j = σ ( 1 − m i m j ) ∆ i j ( 2.4 ) w_{ij}=\frac{σ(1-\mathbf{m}_i\mathbf{m}j)}{∆{ij}} (2.4) wij=∆ijσ(1−mimj)(2.4) 其中耦合系数 σ < 0 表示双层反铁磁耦合，单位为 J/m^2^。m ~i~ 和 m ~j~ 为两铁磁层之中近邻单元格的单位磁化强度，∆~ij~ 则是单元格 i 到单元格 j 方向上的单元格尺寸（通常为间隔层的厚度）。
3. 退磁能

由磁矩之间的偶极相互作用导致的退磁能又称为静磁能，是一种经典效应，具有长程作用范围。其能量密度表达式为：
w d e m = − u 0 M s 2 m ⋅ H d e m ( 2.5 ) w_{dem}=-\frac{u_0M_s}{2}\mathbf{m}\cdot\mathbf{H}{dem} (2.5) wdem=−2u0Msm⋅Hdem(2.5) 实际上，磁体自身的磁化强度会产生偶极磁场，对于给定的磁体的磁化强度，可以通过求解麦克斯韦方程组来找到偶极磁场的分布，即满足： ∇ ⋅ B = 0 \nabla\cdot\mathbf{B}=0 ∇⋅B=0， ∇ × H d e m = 0 \nabla\times\mathbf{H}{dem}=0 ∇×Hdem=0 以及 B = u 0 ( H d e m + M ) \mathbf{B}=u_0(\mathbf{H}_{dem}+\mathbf{M}) B=u0(Hdem+M)。磁体内部的偶极磁场为退磁场 H ~dem~，而外部的则为杂散场（stray field）。退磁能的存在会使磁体中会出现许多将磁畴分隔开的磁畴壁，并最大限度地减少磁体外部的杂散场。
4. 磁晶各向异性能

磁晶各向异性起源于自旋轨道耦合相互作用，同时取决于晶体结构，它的存在使磁体的磁滞回线出现方向依赖性。沿着磁体的易轴方向施加较小的磁场能将之轻易磁化，反之，沿着其难轴方向则需要较大的磁场才能将之磁化。对于最简单的磁晶单轴（uniaxial）各向异性来说，其能量密度表达式为：
w u a = − K ( m ⋅ u ) 2 ( 2.6 ) w_{ua}=-K(\mathbf{m}\cdot\mathbf{u})^2 (2.6) wua=−K(m⋅u)2(2.6) 其中系数 K > 0，单位为 J/m^3^，u 为易轴方向。显然，磁化强度倾向于和易轴方向共线来使各向异性能最小，即它们相互平行或反平行时的各项异性能相同。然而，当 K < 0 时，上式则用于表示面内各向异性能的能量密度，此时的 u 则表示易平面的法线方向，磁化强度会倾向垂直于 u 来使各向异性能最小化。

此外，对于磁晶立方（cubic）各向异性来说，其能量密度表达式为：
w c a = − K ( m 1 2 m 2 2 + m 2 2 m 3 2 + m 1 2 m 3 2 ) 2 ( 2.7 ) w_{ca}=-K(m_1^2m_2^2+m_2^2m_3^2{+m_1^2m_3^2)}^2 (2.7) wca=−K(m12m22+m22m32+m12m32)2(2.7) 其中 m i = m ⋅ u i m_i=\mathbf{m}\cdot\mathbf{u}_i mi=m⋅ui，易轴方向 u ~1~、u ~2~ 和 u ~3~ 之间满足 u 3 = u 1 × u 2 \mathbf{u}_3=\mathbf{u}_1\times\mathbf{u}_2 u3=u1×u2。
5. DMI能

不同于对称的交换相互作用，Dzyaloshinskii和Moriya提出在空间反演对称性破缺的材料中存在着不对称的交换耦合，即两个自旋的交换（S ~i~ ↔ S ~j~）会改变相关能量的符号，并划分为界面型（interfacial）和体型（bulk）两种基本的反演对称性破缺。对于如Co/Pt、Fe/Ir和Fe/W等FM/HM薄膜异质结来说，其界面DMI能的能量密度表达式为：
w i D M I = ( ± ) D ( m ⋅ ∇ m z − m z ∇ ⋅ m ) ( 2.8 ) w_{iDMI}=(\pm)D(\mathbf{m}\cdot\nabla m_z-m_z\nabla\cdot\mathbf{m}) (2.8) wiDMI=(±)D(m⋅∇mz−mz∇⋅m)(2.8) 对于如MnSi、FeCoSi和FeGe等具有B20结构的磁性材料来说，其体DMI能的能量密度表达式为：
w b D M I = ( ± ) D m ⋅ ( ∇ × m ) ( 2.9 ) w_{bDMI}=(\pm)D\mathbf{m}\cdot(\nabla\times\mathbf{m}) (2.9) wbDMI=(±)Dm⋅(∇×m)(2.9) 其中DMI的强度 D 与描述原子尺度自旋手性耦合的DM矢量的模成正比，单位为 J/m^2^。DMI的存在会使紧邻磁矩倾向于相互垂直来让能量最小化，存在DMI的磁体即为手性磁体。

2.1 静态微磁学

静态微磁学主要关注磁体系的稳态或亚稳态磁化分布，而不太需要关注达到该状态的具体过程，通常用于分析样品的磁性能量、偶极场分布和磁滞回线等相对整体的特性。尽管前文中描述了磁矩在每种相互作用下为了最小化相应能量而呈现的各种排列方式，然而考虑到磁体系中往往共存着多种相互作用，所以为了整个磁体系的能量最小化，这些相互作用会彼此竞争、相互妥协。可以设想一些相互作用共存的简单情况：（1）仅存在交换相互作用和外加磁场时，所有磁矩都指向外加磁场的方向既能使交换能最小化，也能使塞曼能最小化。如图2-2（a）和（b）所示，为了遵循能量最小化原理，随机磁化分布会演变成指向外加磁场的均匀磁化分布。（2）仅存在交换相互作用、单轴各项异性以及指向易轴特定方向的外加磁场时，所有磁矩都会指向外加磁场和易轴的共同方向，以确保交换能、各向异性能、塞曼能同时最小化。图2-2（c）考虑的各向异性类型为垂直磁晶各向异性。

(a) 随机磁化分布，(b) 塞曼能和交换能共存，(c) 塞曼能和交换能以及垂直各向异性能共存

图2-2 磁矩在共存的相互作用下的排列方式

实际上，为了分析磁体系处于更加复杂的多种相互作用下的稳态磁化分布，考虑其总能量密度 w ~total~(m ) 的一阶变分导数，也是所有相互作用的等效磁场之和，即总有效磁场 H ~eff~ 为[35]：
H e f f = − 1 u 0 M s δ w t o t a l ( m ) δ m ( 2.10 ) \mathbf{H}{eff}=-\frac{1}{u_0M_s}\frac{\delta w{total}\left(\mathbf{m}\right)}{\delta\mathbf{m}} (2.10) Heff=−u0Ms1δmδwtotal(m)(2.10) 当磁化强度平行于有效场时，便认为是稳定的磁化分布，即满足： m × H e f f = 0 \mathbf{m}\times\mathbf{H}{eff}=0 m×Heff=0。然而在实际情况中，我们通常只能给出一个预设的磁化分布，于是可以通过共轭梯度法迭代求解能量的下降路线，从而得到能量达到极小值时的磁化分布。在迭代过程中，若磁化强度受到的面内转矩低于临界值： m × H e f f × m < T c \mathbf{m}\times\mathbf{H}{eff}\times\mathbf{m}<\mathbf{T}_c m×Heff×m<Tc，便被认为是达到了稳态。一般情况下，满足临界转矩 T ~c~ 低于0.1 A/m的稳态磁化分布是合理的[101]。

2.2 动态微磁学

动态微磁学需要追踪磁化强度在外加激励下随时间的变化，即磁化动力学。微磁学核心方程之一的Landau-Lifshitz-Gilbert（LLG）方程描述了磁化强度随时间的演变过程[16]：
d M d t = − γ ( M × H e f f ) + α M s M × d M d t ( 2.11 ) \frac{d\mathbf{M}}{dt}=-\gamma(\mathbf{M}\times\mathbf{H}_{eff})+\frac{\alpha}{M_s}\mathbf{M}\times\frac{d\mathbf{M}}{dt} (2.11) dtdM=−γ(M×Heff)+MsαM×dtdM(2.11) 其中 γ 是旋磁比，α 为吉尔伯特阻尼系数。LLG方程的物理图景可以借助经典的宏自旋（macrospin）模型给描绘出来，其总体效果表现为磁矩围绕有效场 H ~eff~ 逆时针进动[16]，如图2-3所示。

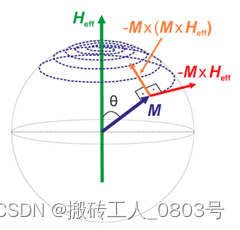
图2-3 LLG方程的物理图景[16]

具体而言，LLG方程右边的第一项表现为磁矩受到面外转矩（红色箭头表示的场矩）的作用而围绕有效场 H ~eff~ 逆时针旋转，因此磁化强度的变化 d M d t \frac{d\mathbf{M}}{dt} dtdM 始终垂直于磁化强度 M 自身，即满足： M ⋅ d M d t = 0 \mathbf{M}\cdot\frac{d\mathbf{M}}{dt}=0 M⋅dtdM=0。LLG方程右边第二项的显式表达式为： M × d M d t = M × ( M × H e f f ) \mathbf{M}\times\frac{d\mathbf{M}}{dt}=\mathbf{M}\times(\mathbf{M}\times\mathbf{H}_{eff}) M×dtdM=M×(M×Heff)，表现为磁矩受到面内转矩（橙色箭头表示的阻尼矩）的作用而靠近有效场，并最终与有效场平行达到稳态。另一方面，由极化电流引入的额外转矩（如Slonczewski型或Zhang-Li型转矩）可以直接追加在LLG方程右边。需要注意的是，对于间隔层为金属的自旋阀来说，通常忽略其较弱的面外转矩（类场矩），而仅考虑其面内转矩（类阻尼矩）。然而对于磁隧道结来说，则必须同时考虑类阻尼矩和类场矩[11]。

从LLG方程的物理图景中可以看到，对有效场的微扰会导致磁矩偏离平衡位置而开始进动。当扩展到整个磁体系中所有的磁矩时，考虑到磁矩之间的进动相位可以是相同或不同的情况，倘若所有磁矩以相同的相位一致进动，则实现了铁磁共振（Ferromagnetic resonance，FMR），此时，相位的空间分布是均匀的。对于本文所关注的具有垂直各向异性的铁磁薄膜来说，其FMR频率的表达式为[73]： f F M R = γ ( 2 K − u 0 M s 2 ) / ( 2 π M s ) f_{FMR}=\gamma(2K-u_0M_s^2)/{(2\pi M}_s) fFMR=γ(2K−u0Ms2)/(2πMs)。若是磁矩之间的进动相位不同，即非一致进动，那么磁化强度的变化就表现为波状的激发，称为自旋波，如图2-4所示[16]。

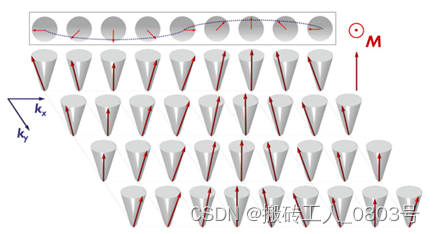
图2-4 磁矩的非一致进动形成自旋波[16]

和其他类型波的描述类似，自旋波的传播方向即为波矢，其频率（能量）和波矢之间的关系即为色散关系。此外，由于自旋波仅存在于磁性材料中，所以其色散关系受波导边界条件和横向宽度的影响比较大[16,102]，如图2-5所示。

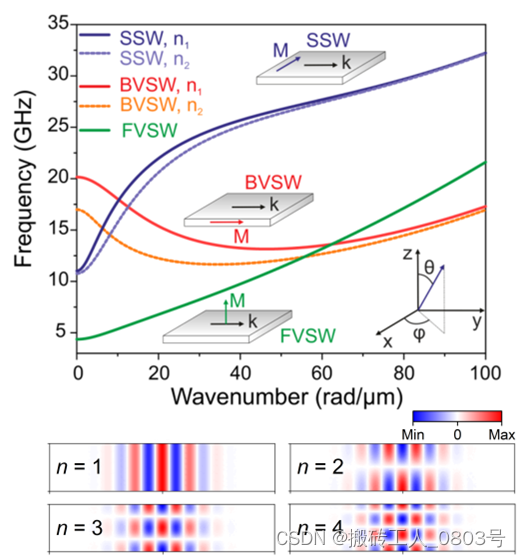
图2-5 自旋波色散关系[16]和 n 阶宽度模[102]

对于由交换相互作用主导的短波长的自旋波来说，其色散关系与静态磁化的方向无关。然而对于由偶极相互作用主导的长波长静磁自旋波来说，其色散关系则依赖静态磁化的方向。具体而言，考虑静磁自旋波在磁化均匀且宽度有限的铁磁薄膜波导中传播，按照波导的静态磁化的方向与波矢的方向之间的关系，从而分为三种模式[16]：（1）静态磁化垂直于波导平面，并且波矢垂直于磁化，即称之为前向体积自旋波（FVSWs），在色散关系中表现为群速度平行于相速度。（2）静态磁化和波矢均位于波导平面内并相互垂直，即称之为表面自旋波（SSWs）或Damon-Eshbach模式，在色散关系中表现为群速度平行于相速度，并且该模式自旋波的振幅会随着与波导表面的距离增加而衰减。（3）静态磁化和波矢均位于波导平面内并相互平行，即称之为后向体积自旋波（BVSWs），在色散关系中表现为负的群速度，且群速度和相速度反平行。另一方面，由于波导的宽度有限，于是自旋波在波导的宽度方向上具有驻波的轮廓，从而根据波腹的数量进一步分为 n 阶宽度模的自旋波[16,102]。不同宽度模的自旋波在色散关系中表现为不同的曲线，如图2-5所示。

2.3 微磁学模拟软件

微磁学模拟软件通常使用有限元法（Finite element method，FEM）或有限差分法（Finite difference method，FDM）来对一个连续的物体进行离散化，其中有限元法使用的是三角形或四面体等基本单元组成的不规则网格，而有限差分法则是使用尺寸相同的单元格组成的网格。

在计算退磁场的过程中时，相较于有限元法，有限差分法在离散弯曲结构时会在其边缘生成一些阶梯状的锯齿，尽管真实样品的边缘同样存在一定的粗糙，但这实际上会导致计算的退磁场存在较大的误差，不过可以通过精细化网格来降低这种误差。此外，有限差分法还可以使用快速傅里叶变换算法来加速计算，所以其模拟速度通常要比有限元法快。

本文使用的微磁学模拟软件是基于有限差分法的OOMMF和MuMax3，接下来将分别介绍这两个软件：
1. OOMMF

OOMMF（Object Oriented Micromagnetic Framework）主要是由美国National Institute of Standards and Technology的Mike Donahue和Don Porter负责开发的微磁学模拟软件[101]。该开源的软件具有C++代码编写的底层以及Tcl/Tk代码编写的用户层，并且可适配Unix、Windows和Mac OS平台，具备高度的可移植性和强大的可扩展性，是目前引用文献最多的微磁学模拟软件。

在使用OOMMF软件的过程中，我们通常使用其主体程序Oxsii来求解由Tcl代码描述的微磁问题，并使用其一系列内置的功能强大的命令行程序来批处理磁化文件，包括批量作差，批量切片，批量转换文件格式等等。
2. MuMax3

MuMax3是由比利时Ghent大学的DyNaMat团队开发和维护的软件[103]。该开源软件利用GPU来加速求解微磁问题，并提供基于浏览器的用户界面，同样支持多平台操作系统。自MuMax3发布以来，由于其具有运行速度快、内置功能丰富等优点，越来越多的研究人员对其青睐有加。

在使用MuMax3软件的过程中，我们通常使用命令行直接运行由Go代码描述的微磁问题文件。和OOMMF不同的是，MuMax3使用Geometry来描述样品形状以及无磁性的缺陷。此外，MuMax3还内置了Voronoi tessellation用于生成晶粒图案以便于模拟空间中随机变化的材料参数。

对于OOMMF和MuMax3输出的磁化文件，则可以借助Ubermag提供的程序包来进行数据后处理[104]，包括对有限差分场进行代数运算、求导和积分等操作。

第三章磁畴壁波导的能带调控

我们在1.2节介绍了近年来与磁畴壁波导相关的研究进展，相比于基于铁磁材料中均匀磁化的传统磁畴波导，畴壁波导中的束缚态自旋波拥有接近于零的截止频率和沿着弯曲畴壁传播的能力。此外，这种具有1D传播特征的束缚态自旋波对样品边缘和其他类型的缺陷也不太敏感，进而拥有更长的相干长度和衰减长度。然而，畴壁波导的这些特点导致难以使用常规方法调控其能带结构，比如周期性刻蚀样品的两侧边[45]，这种边缘调控方法对束缚态自旋波的传播影响很小，所以并不适用于调控畴壁波导的能带结构。另一方面，考虑其他类型的磁纹理阵列来引入周期性调控也不太合适[55--57]，因为这些磁纹理会扰乱甚至破坏作为自旋波通道的畴壁。目前的关键问题是设计一种有效的调控方案，使调制模块能与束缚态自旋波相互作用，并显著地影响其传播。

基于上述问题，我们设计了一种array-on-film结构的磁振子晶体，以期望对畴壁波导的能带进行深度调控。该磁体系中持有畴壁波导的下层长条带以及可重构磁化分布的上层短条带阵列通过偶极相互作用耦合，并存在Loop、C-C、C-up和C-down四种静态磁化构型。通过微磁模拟，我们首先研究了独立畴壁波导中传播的束缚态自旋波的频率谱、色散关系等特性，接着我们对比研究了这四种磁化构型分别对能带结构的影响。模拟结果表明虽然C-C、C-up、C-down三种构型的畴壁波导是弯曲起伏的，且引入了非周期震荡的势场，但是它们对束缚态自旋波的频率谱和传输特性的影响却很小。然而当磁体系处于具有磁通闭合特征的Loop构型时，畴壁波导的能带结构中形成了带隙。此外，通过调节磁体系的物理几何参数、磁性参数和磁化分布也可显著改变带隙的位置、数量和宽度。通过控制变量的思想，我们分别研究了上层短条带阵列辐射的静态杂散场和动态杂散场对带隙打开的贡献。研究表明畴壁波导中由于静态杂散场的耦合出现了正弦状的周期势场，导致色散曲线在布里渊区边界发生折叠交叉从而形成了带隙，然而动态杂散场的耦合则会让处于带隙中且模式匹配的自旋波共振增强，从而让自旋波穿透周期势场并在带隙中形成狭窄允带。

在最近的一项研究中，Yu等人理论上设计了一种不可移动的人工畴壁波导[39]，其截止频率以下的Goldstone模式自旋波被禁止，从而形成了单个带隙。相比之下，本文提出的调控能带的方法可以应用于更广泛的自旋波波导，例如无论是基于天然的还是基于人工的畴壁波导或Damon-Eshbach模式的波导，且并不仅限于在能带中打开单个带隙。

3.1 微磁模型和磁化构型

我们设计的适用于畴壁波导的array-on-film结构的磁振子晶体如图3-1（a）所示，该结构包含具有垂直磁各向异性（Perpendicular magnetic anisotropy，PMA）的铁磁层FM1和FM2，一个非磁性间隔层Spacer，以及重金属层HM1和HM2。其中FM2/HM2是一系列等间隔分布的纳米条带阵列，单根纳米条带的宽度是 p ~1~，纳米条带之间的间隔距离为 p ~2~，于是该条带阵列的周期为 p = p ~1~ + p ~2~，并具有 N 个重复周期。此处由间隔层物理分隔开的FM1和FM2之间只存在偶极耦合而不存在层间交换耦合。需要注意的是，夹在重金属层和间隔层之间的每个铁磁层都有两个非对称界面，这种非对称界面会通过强自旋轨道相互作用在铁磁层中引入Dzyaloshinskii-Moriya相互作用（DMI）[105,106]。当两重金属层HM1和HM2是相同的材料时，比如Pt，则重金属层与铁磁层之间的堆叠顺序会影响铁磁层中DMI的符号。比如此处的HM1/FM1和FM2/HM2会导致FM1和FM2中的DMI符号相反，即FM1中的 D > 0，但FM2中的 D < 0。

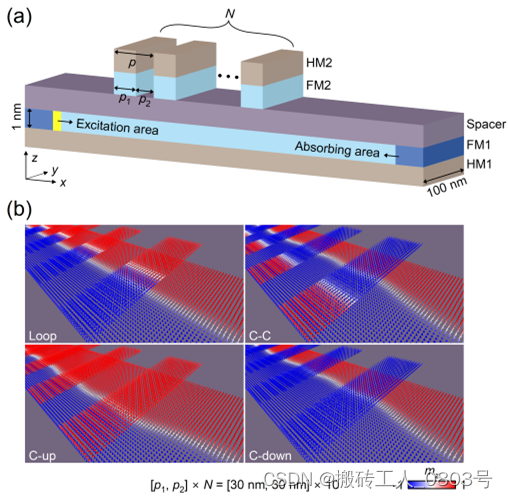
图3-1 器件结构和静态磁化构型

我们在此处选取HM/FM体系典型的磁性参数[107--109]：饱和磁化强度 M ~s~ = 580 kA/m，交换系数 A = 15 pJ/m，PMA常数 K ~u~ = 0.8 MJ/m^3^，FM1中的DMI数值为3.5 mJ/m^2^，FM2中的DMI数值为-3.5 mJ/m^2^。我们设置吉尔伯特阻尼系数 α 为0.015，但对于图中蓝色的自旋波吸收区域来说，则是将其阻尼系数设为从0.1增加到0.5以用于抑制自旋波的反射。图中黄色的狭窄区域（10 × 100 × 1 nm^3^）表示的是条带天线施加局域磁场用于激发自旋波的区域，激发磁场的形式为 h r f = h 0 sin ⁡ ( 2 π f c ( t − t 0 ) ) 2 π f c ( t − t 0 ) x ^ \mathbf{h}{rf}=h_0\frac{\sin{\left(2\pi f_c\left(t-t_0\right)\right)}}{2\pi f_c\left(t-t_0\right)}\hat{x} hrf=h02πfc(t−t0)sin(2πfc(t−t0))x^，其中 h ~0~ = 7950 A/m，f ~c~ = 80 GHz，t ~0~ = 1 ns。注意条带天线的激发区域是根据模拟需求而变化的，比如示意图中的激发区域就位于距离FM1左端200 nm处，以用于分析向右传播的自旋波的传输特性曲线。此外，当激发区域位于FM1的中心时，则可以用于分析自旋波的整体色散关系。激发磁场选用sinc形式的原因是它能按照同等功率激发在截止频率下的所有自旋波频率。此外，sinc激发磁场在模拟中的持续时长为12 ns，且每间隔6 ps就保存一次磁化文件用于数据后处理。当磁体系处于外加激励的动态模拟阶段时，sinc激发磁场诱导的磁化动力学由Landau-Lifshitz-Gilbert（LLG）方程[110,111]描述：
∂ m ∂ t = − γ m × H e f f + α m × ∂ m ∂ t ( 3.1 ) \frac{\partial\mathbf{m}}{\partial t}=-\gamma\mathbf{m}\times\mathbf{H}{eff}+\alpha\mathbf{m}\times\frac{\partial\mathbf{m}}{\partial t} (3.1) ∂t∂m=−γm×Heff+αm×∂t∂m(3.1) 其中，m 是磁化强度 M (r , t ) 的归一化表示，r 表示位置，t 是时间。γ 是旋磁比， H e f f = − 1 μ 0 δ E δ M \mathbf{H}_{eff}=-\frac{\mathbf{1}}{\mu_0}\frac{\delta E}{\delta\mathbf{M}} Heff=−μ01δMδE 是由能量和磁化强度决定的有效磁场。该磁体系中所涉及的能量 E 由如下相互作用贡献，包括：海森堡交换相互作用（E ~x~）、偶极-偶极相互作用（E ~di~）、垂直磁各向异性（E ~a~）、Dzyaloshinskii-Moriya相互作用（E ~DMI~）以及塞曼相互作用（E ~Z~）。

我们使用OOMMF[101,112]进行数值模拟，整个磁体系的模拟空间设置为2000 × 100 × 3 nm^3^，并且设置2 × 2 × 1 nm^3^的单元格对整个空间进行离散化，用于确保单元格尺寸小于交换长度 l e x = 2 A ( μ 0 M s 2 ) ≈ 8.4 n m l_{ex}=\sqrt{\frac{2A}{\left(\mu_0M_s^2\right)}}\approx8.4\ nm lex=(μ0Ms2)2A ≈8.4 nm 和畴壁厚度 Δ = A ( K u − 1 2 μ 0 M s 2 ) ≈ 5.0 n m \Delta=\sqrt{\frac{A}{(K_u-\frac{1}{2}\mu_0M_s^2)}}\approx5.0\ nm Δ=(Ku−21μ0Ms2)A ≈5.0 nm。OOMMF既可以通过能量最小化原理得到该磁体系的静态磁化构型，也可以通过求解LLG方程对磁体系弛豫足够长的时间让其达到稳态。

首先，如图3-1（b）所示，我们得到了该磁体系的四种静态磁化构型：Loop、C-C、C-up和C-down。当磁体系处于Loop构型时，FM1和FM2磁畴内的磁矩排列方向相同，但畴壁内的磁矩排列方向却是相反，即呈现出偶极耦合的铁磁双层特有的磁通闭合特征。对于其余的C-C、C-up和C-down构型来说（按照畴壁内磁矩的排列形状命名），FM1和FM2存在一个磁畴中的磁矩以头对头或者尾对尾的方式排列，导致FM1中与FM2磁矩平行的另一磁畴为了减少静磁能而膨胀，从而使FM1中的畴壁偏离中心轴线并变得局部弯曲。由于Loop构型的磁通闭合特征有助于减少静磁能，因此Loop构型能稳定存在。事实上，类似的磁化构型在具有间隔层的铁磁双层膜体系已被广泛研究，并被证明在提高器件性能方面发挥着重要作用[49,58,113--115]。

3.2 带隙打开的现象

为了体现铁磁双层FM1|FM2处于Loop构型时对FM1中畴壁波导能带结构的影响，我们首先分析了FM1中独立畴壁波导的频率谱和色散关系，即考虑此处不存在FM2的情况作为对照组。在FM1中间处施加局域的sinc激发磁场并保存一系列的磁化文件后，我们使用Python程序对减去基态磁化后的动态磁化文件进行数据后处理[116]：选取动态磁化强度的 x 分量用来表征自旋波；沿畴壁波导的长度方向进行空间采样；通过1D的FFT和2D的FFT分别得到频率谱和色散关系，如图3-2（a）和（b）所示。

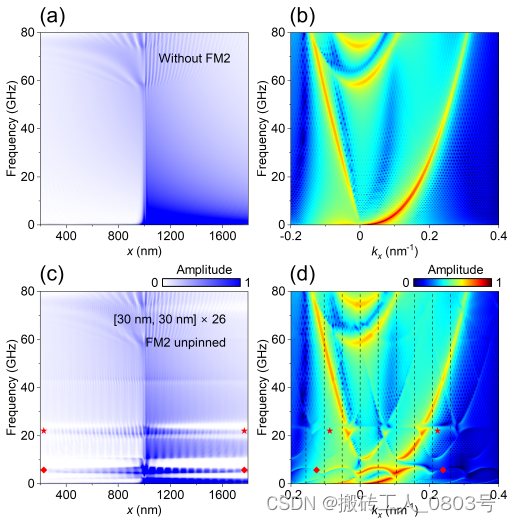
(a) 独立畴壁波导的频率谱，(b) 独立畴壁波导的色散关系，(c) Loop构型中畴壁波导的频率谱，(d) Loop构型中畴壁波导的色散关系

图3-2 Loop构型的带隙打开

从频率谱中可以看到由于阻尼耗散的作用，自旋波的振幅随着传播距离的增加而衰减。考虑束缚态自旋波的寿命为 τ = ( 2 π α f ) − 1 \tau={(2\pi\alpha f)}^{-1} τ=(2παf)−1，于是其衰减长度为 s = α f d f d k x s=\alpha f\frac{df}{dk_x} s=αfdkxdf，即衰减长度表现出频率依赖性[117,118]。对于使用条带天线来激发自旋波来说，由于每个自旋波频率的实际激发效率是与其自身波矢有关[119]，所以即便使用sinc激发磁场以同等功率激发所有的自旋波频率，激发出来的自旋波的实际强度也并不是均匀的。这些因素共同导致了自旋波振幅随 f ，x 和 k ~x~ 轴呈现非均匀分布的特征。此外，从色散关系中还可以看到畴壁中的束缚态自旋波和磁畴中的体态自旋波的截止频率分别为 ~0 GHz和 ~60 GHz，左右不对称的色散关系是由于磁体系中存在的DMI导致了左（k ~x~ < 0）、右（k ~x~ > 0）两支束缚态自旋波是非互易性的[28,29]。

接下来分析磁体系中存在FM2的情况，且考虑FM2的周期满足 [p ~1~, p ~2~] × N = [30 nm, 30 nm] × 26。当磁体系处于Loop构型时，我们按照相同的流程获取了FM1中畴壁波导的频率谱和色散关系，如图3-2（c）和（d）所示。可以看到在频率谱和色散关系中打开了几个非常明显的带隙，具体而言，带隙在频率谱中表现为拒绝频率带，在色散关系中表现为曲线的不连续。

3.3 带隙打开的起源

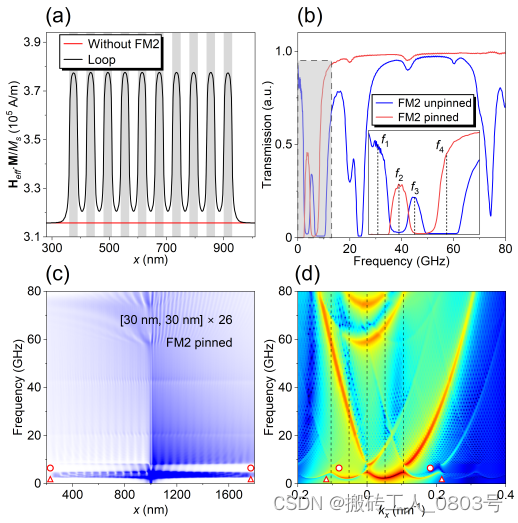
(a) FM2条带阵列的静态杂散场引入周期势场，(b) Loop构型的传输特性曲线，(c) FM2磁化固定时畴壁波导的频率谱，(d) FM2磁化固定时畴壁波导的色散关系

图3-3 Loop构型中固定和不固定FM2的磁化

为了理解这些带隙的形成原因，我们分析了不存在FM2的独立畴壁波导和Loop构型中的畴壁波导两种情况下沿着畴壁中心（y = 50 nm）的势场分布。从图3-3（a）可以看到独立畴壁的势场是沿着长度方向均匀分布的，然而Loop构型的势场曲线由于FM2条带阵列的静态杂散场耦合从而呈现出周期振荡的轮廓，并且总体上高于独立畴壁的势场。为了理解该周期势场对打开带隙的贡献，我们遵循控制变量的思想设计了两组模拟：第一组模拟是在使用sinc磁场激发FM1的过程中，将FM2的磁化固定住，以禁止其对FM1的动态杂散场响应。在第二组模拟中，我们将FM2移除并对余下独立的FM1施加一个偏置磁场施用于代替FM2的静态杂散场，由于该偏置磁场和FM2的静态杂散场完全等效，所以FM1畴壁内的势场曲线和Loop构型的势场曲线完全相同。虽然这两组模拟采用了不同的方式来研究FM2的静态杂散场对打开带隙的贡献，但实际上得到的频率谱和色散关系都是相同的，如图3-3（c）和（d）所示。这里出现的两个非常明显的带隙分别位于布里渊区中心和第一布里渊区边界，此处布里渊区中心与 k ~x~ = 0的偏移是由于自旋波的非互易性导致的[47,120]。

无论是在天然的还是在人工的周期性结构中传播的自旋波，当其满足布拉格条件时，都会由于周期势场的作用而发生大量的散射[40,42,47]。随后便是入射自旋波与反射/衍射自旋波干涉，导致了驻波的形成，从而在能带中表现为布里渊区边界处带隙的打开现象[40,42,47]。在一些情况下，原始模式的入射自旋波可能会由于布拉格衍射而散射成不同的本征模，从而导致两支不同模式自旋波的色散曲线反交叉[45]。这种由模式之间的相消干涉导致了另类带隙的打开，并且这类带隙是远离布里渊区边界的[45]。

R. A. Gallardo等人最近的一项研究表明，对于存在周期性DMI的手性磁振子晶体来说，由于其内部传播的入射自旋波和反射自旋波具有不同的波长，所以形成的带隙会偏离布里渊区边界[120]。但对于本文的磁振子晶体来说，自旋波是束缚在畴壁内的狭窄势阱内，其波束宽度约为几十纳米[28--34,36]。所以，自旋波在畴壁波导中只有最低阶的基本模式，而不存在高阶模式。由此根据这一事实，我们可以排除畴壁波导中由于模式间的相消干涉而形成带隙的可能。

基于上述分析，可以得到如下结论：图3-3（c）中带隙和振幅的不对称分布是由于DMI导致的[120]。图3-3（d）中圆圈标注的上带隙是位于色散曲线的折叠交叉处，所以可以判断这个带隙起源于周期性势场以及布拉格反射导致的自旋波相消干涉。至于三角形标注的下带隙则是起源于畴壁波导内部势场的增加，如图3-3（a）中的黑色和红色曲线所示，这种带隙改变了畴壁波导截止频率接近于零的特性，与使用外加磁场调节传统波导的截止频率的情况类似。实际上，与这个带隙起源类似的是，可以修饰天然畴壁的面内磁各向异性（In-plane magnetic anisotropy，IMA）参数从而得到截止频率不为零的人工畴壁波导[39]。

为了示例性地展示畴壁波导内部势场的增加会提高截止频率，我们按照图3-4（a）所示的方式对独立的畴壁施加一个y 方向的局域偏置磁场（x 范围：234 ~ 1764 nm，y 范围：40 ~ 60 nm），两组示例的偏置磁场幅值分别为30 kA/m和90 kA/m。从图3-4（b）中可以看到，畴壁内处于该偏置磁场空间范围内的势场明显增加。两组示例得到的色散结果分别如图3-4（c）和（d）所示，可以看到内部势场的增加确实是提高了畴壁波导的截止频率。然而正如图3-2（c）和（d）所示，FM1和FM2之间的动态耦合可以显著改变能带结构，所以FM2的作用不仅仅是在FM1中引入静态的周期势场[115]。

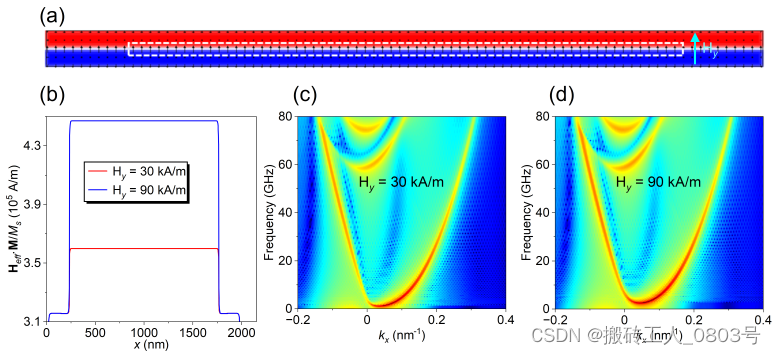
(a) 对独立畴壁波导施加局域的均匀磁场，(b) 外加磁场空间范围内局域增高的势场曲线，(c) 在外加磁场 H~y~ = 30 kA/m时的色散关系，(d) 在外加磁场 H~y~ = 90 kA/m时的色散关系

图3-4 局域外加磁场导致畴壁波导的截止频率提高

上述分析阐述了FM2的静态杂散场对带隙打开的贡献，接下来便是考虑FM2的动态杂散场对能带结构的影响。我们首先分析了FM2磁化分别固定和不固定时磁振子晶体的传输特性，具体取值为透射自旋波的振幅与独立畴壁波导内的参考振幅的比值，需要注意的是空间采样范围应当跳过FM2条带阵列覆盖的范围。图3-3（a）展示了这两种情况的传输特性曲线，从而可以更直观地对比带隙差异，图中的标注的频率点 f ~1~、f ~2~、f ~3~ 和 f ~4~ 是属于两种情况的禁带频率或允带频率。

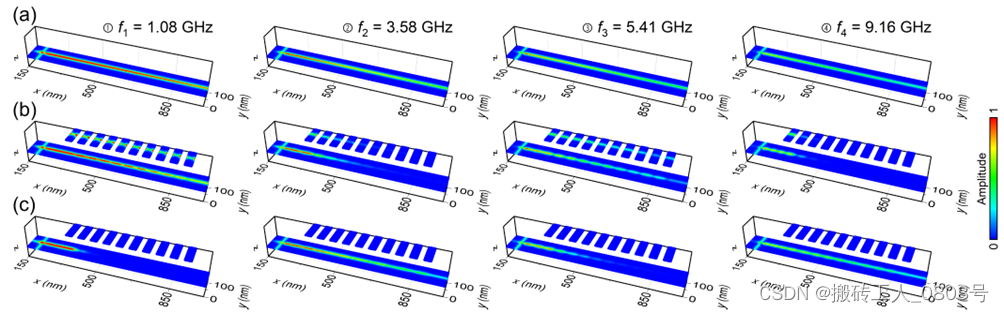
图3-5 允带和禁带各自的模式分布

为了体现出FM2对FM1束缚态自旋波的调制效果，通过对磁体系中所有单元格进行1D的FFT，并提取它们在上述四个频率点相应的振幅，于是便得到了图3-5所示的振幅空间分布。图中考虑了磁体系的三种情况：图3-5（a）表示FM2不存在的情况；图3-5（b）表示FM2磁化未固定的情况；图3-5（c）则表示FM2磁化固定的情况。当不存在FM2时，束缚态自旋波沿着FM1中畴壁传播且其振幅缓慢衰减，在模式分布中没有出现任何波节，表现出非常明显的1D传播特征。然而当存在FM2时，模式分布中出现了拍频现象，这表明存在着自旋波干涉[121]。还可以看到由于自旋波干涉，频率处于带隙范围内的自旋波传播到条带中心时振幅最小。

回顾图3-2（d）未固定FM2磁化的色散关系并结合上述频率点的模式分布，现在我们可以推断FM2动态杂散场对带隙打开的贡献。从图3-2（d）中很容易看出色散曲线大约在2 ~ 11 GHz和19 ~ 24 GHz发生了折叠交叉，并且这两个频率范围各自包含一对带隙和间隔的一个狭窄允带（上、下狭窄允带分别用星形和菱形标注）。所以在我们看来，这两对带隙都起源于布拉格反射，然而带隙对之间的这两个狭窄允带则是起源于偶极耦合的array-on-film共振增强的集体模式。当FM1畴壁内的自旋波与FM2条带阵列的畴壁内的自旋波实现模式匹配时，自旋波便能穿过这个周期势场，于是便促进了这种带隙中传播态的出现。这个模式匹配涉及自旋波的频率、波长和相位匹配。

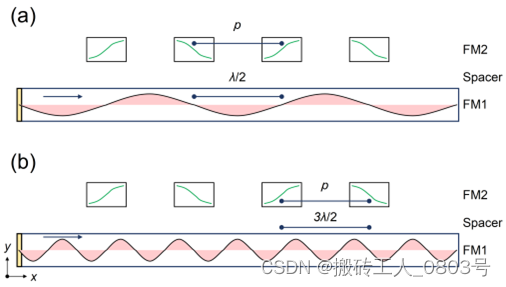
(a) 波长和周期满足 p = λ /2，(b) 波长和周期满足 p = 3λ /2

图3-6 带隙内传播态的共振模式匹配条件

模式匹配的示意图如图3-6所示，这里展示了两个具体的例子：在入射自旋波的波长 λ 满足模式匹配的条件后，比如：p = λ/2 、p = 3λ/2 ，FM2每一个条带由于偶极相互作用被动激发出自旋波，并最终与正下方FM1中自旋波同步。此时FM2每一个条带中两端的自旋波相位相反，但紧邻条带的相位相同，于是FM2畴壁波导中诱导的自旋波就会和FM1畴壁波导内传播的自旋波发生共振增强，从而辅助自旋波穿过周期势场。然而，FM2的磁化一旦固定，满足布拉格反射条件 nλ = 2p （n = 1，2，3...）的自旋波则被周期势场阻挡。

值得注意的是，Chuanpu Liu等人在实验上设计了周期性排列的Co纳米条带下方的Y~3~Fe~5~O~12~（YIG）波导，结果表明波导内群速度高达2600 m/s的短波长（低至 λ = 50 nm）自旋波能长距离传播[115]。在他们的情况中，上方条带阵列的动态偶极场在磁畴波导中诱导出自旋波，这些自旋波的波数是量子化的而且与阵列的周期（a ）相关联，表示为 a = n(λ/2) ，其中 n 是偶数（n = 2，4，6...）。在我们的情况中，存在一个可类比的关系 p = n(λ/2) ，但 n 可以是奇数或偶数（n ＝ 1，2，3...），n 取值的差异是由于独特的边界条件导致的。在他们的磁体系中，上方的几个条带在下方波导中激发自旋波的同时被更宽的共面波导天线所激发。然而我们的磁体系中则是使用外加磁场直接激发波导中的自旋波，当自旋波到达条带阵列时，条带阵列内部的条带和连接相邻条带的局部波导凭借自旋波的动态偶极场来相互激发。条带阵列的激发模式决定了每个条带中自旋进动的相位关系，这些相位关系为波数的量子化建立了边界条件。

3.4 能带结构的影响因素

3.4.1 几何周期参数对能带结构的影响

接着便是需要考虑几何周期参数对Loop构型能带结构的影响，于是我们额外设计了三组模拟：第一组模拟中让 p ~1~ 和 p ~2~ 保持相等长度（即 p ~1~ / p ~2~ = 1），但调节总的周期长度 p ；第二组模拟中让 p ~1~ 保持为30 nm并调节 p ~2~ 的长度；第三组模拟则是让 p ~1~ 和 p ~2~ 都等于30 nm，但增加总的周期 N 。

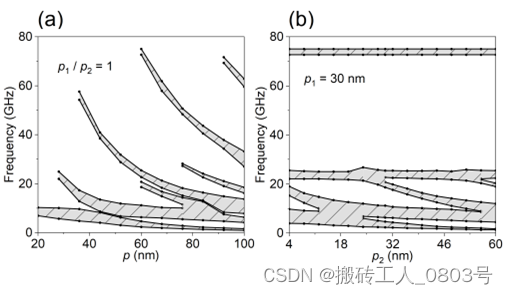
(a) 维持 p ~1~ / p ~2~ = 1 并改变 p ，(b) p ~1~ 保持为30 nm并调节 p ~2~ 的长度

图3-7 带隙关于周期参数的相图

模拟得到的允带和带隙的相图结果如图3-7所示，其中阴影表示带隙，空白则表示允带。第一组模拟结果表明，随着周期 p 的增加，能带中出现了更多的带隙，并且带隙的中心位置也随之下降，这可归因于布里渊区的收缩。第二组模拟结果表明 p ~2~ 的变化会使能带结构发生复杂的演化，其内的带隙相互合并和分裂，但也存在中间的一些带隙和顶带隙没有发生明显变化。第三组模拟结果则表明随着 N 的增加，图中所有的带隙变得越来越清晰明显，这和典型磁振子晶体的特性是类似的。

3.4.2 磁化构型对能带结构的影响

通过使用磁极辐射的杂散场[122]或者使用局域的自旋电流[36]，FM2条带阵列中每个条带都能实现从Loop构型切换到余下的C-C、C-up和C-down构型。如前所述，为了减少静磁能，这三种构型中畴壁波导都是适当弯曲的。图3-8（a-c）的上面板分别展示了磁体系处于这三种构型时FM1的势场分布，需要注意的是，在图中隐藏磁畴区域的势场分布是为了更清晰地对比畴壁区域的势场变化。下面板则是对上面板畴壁区域的势场在 y 方向取平均，便得到了沿 x 方向的平均势场曲线。可以很明显地看到弯曲的畴壁区域的势场分布不再均匀，其平均势场曲线存在非周期的振荡特征并且总体上低于独立畴壁的势场（对比图3-3（a）的势场数值）。

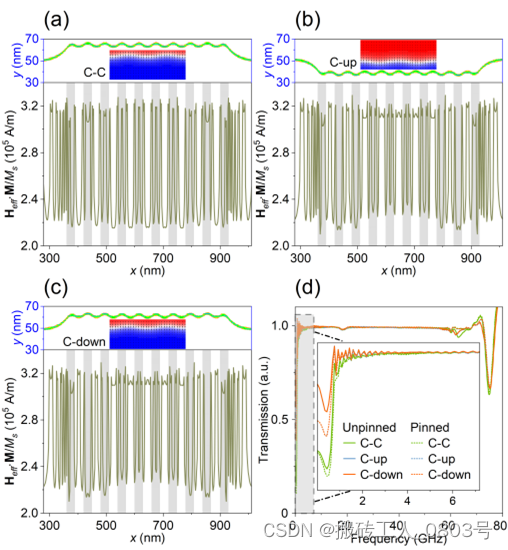
(a) C-C构型的势场，(b) C-up构型的势场，(c) C-down构型的势场，(d) 传输特性曲线

图3-8 磁化构型对传输特性曲线的影响

图3-8（d）是磁体系处于这三种构型时的传输特性曲线，与图3-3（a）Loop构型的传输特性曲线中存在带隙相反，在这三种构型中，~60 GHz以下频率的自旋波可以几乎没有损耗地沿着弯曲的畴壁传播，而且从FM2磁化固定的传输特性曲线来看，FM2的动态杂散场对传输特性曲线的影响非常小。

如图3-9（a-c）所示，我们也分别为C-C、C-up和C-down三个构型选取了四个频率点的模式分布，可以看到尽管弯曲的畴壁区域存在非周期振荡的势场，但自旋波依然能丝滑地穿过FM2所覆盖的范围。

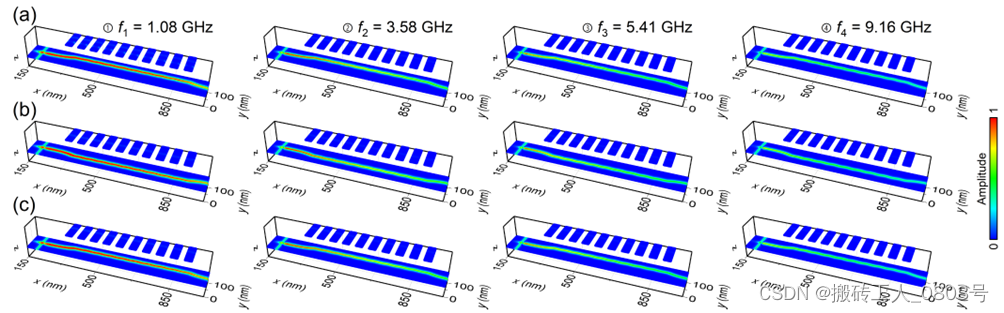
(a) C-C构型，(b) C-up构型，(c) C-down构型

图3-9 特定频率的模式分布

3.4.3 弯曲磁振子晶体对能带结构的影响

为了节省器件的内部空间，实际的磁振子电路会不可避免地弯曲或折叠[22,36]，因此有必要确保所设计的磁振子晶体在弯曲几何结构中也能保持良好的性能。为了验证该预期，我们考虑FM1存在一个90°的弯曲，此时的磁振子晶体如图3-10（a）所示。

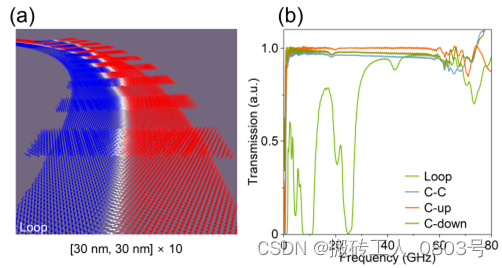
(a) 90°弯曲的Loop构型，(b) 四种构型的传输特性曲线

图3-10 检验几何弯曲波导中的周期势场

这里设置的模拟空间为842 × 842 × 3 nm^3^，FM2中的所有条带都沿着弯曲的FM1的径向方向等间隔排列。在图中所示的Loop构型中，FM1的畴壁是跟随整体方向同步弯曲的，FM2的畴壁是直接位于FM1的畴壁上方，且二者的磁化方向相反。此外，弯曲几何中的C-C、C-up和C-down也是如前文笔直几何中所述的那般无二。因此，这四种构型在弯曲几何中的磁矩排列方式类似于笔直几何的情况，并没有本质的差异。弯曲磁振子晶体的传输特性曲线如图3-10（b）所示。当磁体系从Loop构型切换到余下的三种构型时，带隙关闭得很明显，所以FM2条带阵列确实也能改变弯曲磁振子晶体的能带结构。

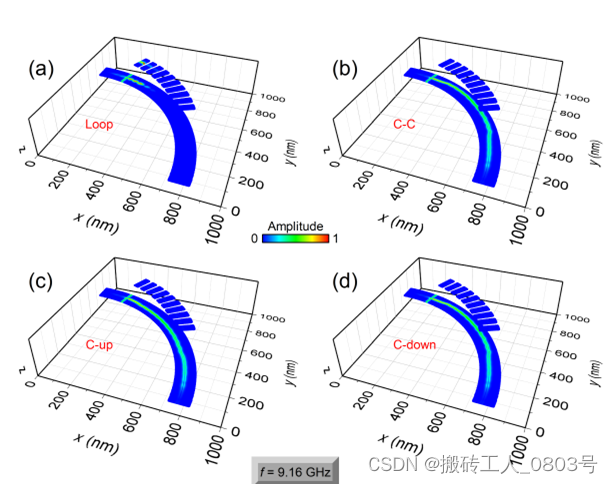
(a) 90°弯曲的Loop构型，(b) 90°弯曲的C-C构型，(c) 90°弯曲的C-up构型，(d) 90°弯曲的C-down构型

图3-11 弯曲结构磁振子晶体的模式分布

我们也分别为这四个构型选取了频率为9.16 GHz的模式分布，如图3-11（a-d）所示。结果表明，除了Loop构型以外，C-C、C-up和C-down三种构型对FM1的畴壁波导中自旋波的影响很小，这与笔直几何的磁振子晶体的情况没有本质的不同。

3.4.4 混合磁化构型对能带结构的影响

由于Loop构型能打开带隙，但C-C、C-up和C-down三种构型则不行，于是这启发我们借助"软"周期参数去调控"硬"周期参数已经固定的磁振子晶体。即对于一个已经制造完成的磁振子晶体来说，可以将FM2中每个条带的磁化构型从Loop切换到其余三种构型来让FM1的畴壁局部变化，从而改变原始的"软"周期参数，促使能带结构发生变化。

例如，对于图3-12（a）和（b）所示的 [p ~1~, p ~2~] × N = [30 nm, 30 nm] × 13 磁体系，我们在两个相邻的Loop条带之间分别插入1和5个C-up条带。在这两种情况下，插入的C-up条带使FM1的畴壁局部弯曲，于是原始的"软"周期参数便发生变化。从频率谱图3-12（c）和（d）中可以看到能带结构中低频率范围内带隙的数量、宽度和位置发生了显著的变化。

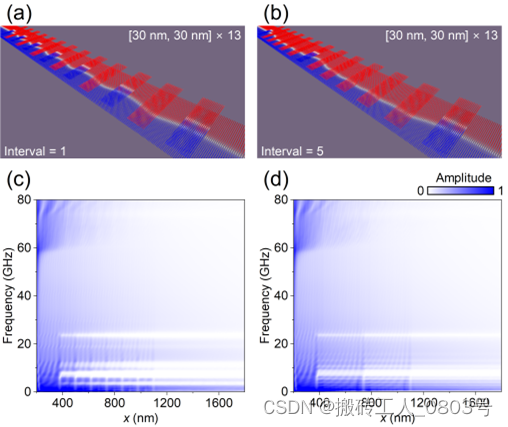
(a) 相邻Loop条带之间插入1个C-up条带，(b) 相邻Loop条带之间插入5个C-up条带，(c) 间隔为1的混合磁化构型的频率谱，(d) 间隔为5的混合磁化构型的频率谱

图3-12 混合磁化构型调控能带结构

3.4.5 间隔层厚度和Dzyaloshinskii-Moriya相互作用对能带结构的影响

我们也分析了间隔层厚度的增加对能带结构的影响，模拟Loop构型磁体系得到的传输特性曲线如图3-13（a）所示。可以看到随着间隔层的增厚，两铁磁层耦合的动态杂散场越来越弱，从而导致带隙越来越窄，甚至两个带隙内由于共振增强形成的窄允带也逐渐关闭。

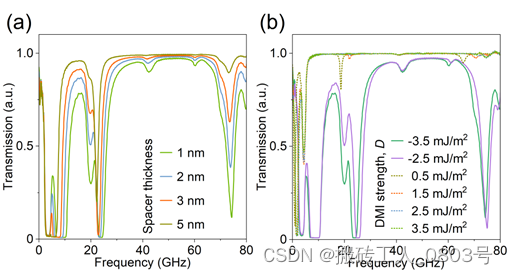
(a) 不同的间隔层厚度下的传输特性曲线，(b) 不同的DMI下的传输特性曲线

图3-13 传输特性曲线与间隔层厚度和FM2的DMI的依赖关系

与重金属层紧邻的铁磁层中DMI的符号取决于重金属的类型以及重金属层相对于铁磁层的堆叠顺序[106]。前文我们假设两重金属层HM1和HM2是相同的材料，于是两铁磁层的DMI的符号是相反的。然而，若HM2使用与HM1不同类型的重金属（例如，Pt → Ta或W），则FM2中DMI的符号将与FM1相同，还可以通过电场和应变等手段有效地调节DMI的强度[123]。此外需要注意的是，FM2中DMI符号的反转会导致FM2内畴壁手性反转，即畴壁中磁矩的方向会反转。具体而言，当FM2的DMI符号转变为正时，FM1和FM2磁畴内的磁矩不受影响，但FM2畴壁内的磁矩会从 +z 指向 -z 转变为从 -z 指向 +z，失去了磁通闭合特征，从而得到一个畸变的Loop构型。FM2的DMI符号和强度对传输特性曲线的影响如图3-13（b）所示，可以看到当仅改变FM2的DMI强度时，带隙的数量没有明显变化，但是带隙的位置有明显的偏移，对于这个现象的解释则可以联想DMI是色散曲线的系数。当FM2的DMI符号变为正时，分析畸变的Loop构型得到的传输特性曲线则完全不一样。可以看到高频率范围内没有明显的带隙，但是在低频率范围内出现了两个狭窄带隙，且对DMI的强度不敏感。

第四章具有固定轨道的自旋转矩纳米振荡器

我们在1.5节介绍了近年来基于斯格明子的自旋转矩纳米振荡器（Spin-torque nano-oscillators，STNOs）的一些相关进展，以及存在的部分亟待解决的问题。对于圆盘磁体系中的铁磁斯格明子来说，通常只有当斯格明子位于圆盘中心时磁体系中才能达到能量极小值的稳态。但这对于需要斯格明子绕圆周轨道旋转的振荡器来说，使用极化电流将斯格明子从圆盘中心驱赶至旋转轨道上会浪费时间和增加功耗。除此之外，由于斯格明子的检测装置通常是基于磁电阻效应制作的，一般只能检测固定区域内斯格明子的存在与否，然而圆盘中斯格明子的旋转轨道会随极化电流变化，这无疑会让检测装置的设计变得更加复杂。

磁畴壁、磁麦纫和磁斯格明子等磁纹理拥有着各具特色的性质，并且不同的磁纹理之间存在着许多微妙的相互作用。通过巧妙地组合多个磁纹理并合理地利用它们之间的相互作用，可以构建单个磁纹理无法实现的全新功能框架和多样化的研究平台。例如，条状畴壁可以辅助斯格明子抵消马格纳斯力从而让其在纳米赛道中直线运动[124--126]，周期排列的磁纹理可以实现可重构的磁振子晶体[56--58]。最近，Panluo Deng等人理论上提出了一种FM/SAFM混合级联结构的斯格明子镜像设备[127]，并通过微磁模拟演示了铁磁斯格明子转变为层间反铁磁耦合的斯格明子对（Skyrmion-Skyrmion pair，SS pair）。

本文中我们设计了一种非对称SAFM纳米圆盘结构的振荡器，对于其内部尺寸不一的上、下铁磁圆盘来说，上圆盘边缘对边缘麦纫（edge-meron）存在向外的吸引力，下圆盘边缘则对斯格明子存在向内的排斥力，当两圆盘的尺寸满足一定比例关系时，层间耦合的麦纫-斯格明子对（Meron-skyrmion pair，MS pair）就可能稳定在上圆盘边缘。接着我们通过微磁模拟和Thiele方程研究了极化电流驱动的MS pair在该器件中的旋转动力学。结果表明，MS pair能始终沿着上圆盘边缘旋转并且拥有着极小的启动时间，其旋转频率不仅受极化电流控制，还取决于器件的几何结构参数和材料的磁性参数。对比典型的基于铁磁斯格明子的振荡器，该振荡器的输出频率远在其之上，并且当注入较大的极化电流时还可以超过基于SAFM圆盘体系中SS pair的振荡器。此外，若往单个振荡器中放置中心对称分布的多个MS pair并使之同步旋转，则可以进一步提高其输出频率。最后，我们测试了随机的垂直各向异性对MS pair动力学的影响，结果表明虽然MS pair的旋转速度会受到扰动，但其旋转轨道不会改变，因此样品中的这种弱无序性参数不会显著改变该振荡器的主要特性。

4.1 微磁模型和磁性参数

我们设计的非对称SAFM纳米圆盘结构的STNO主要由固定层、自由层和间隔层组成，如图4-1（a）所示。在该柱状STNO中，1 nm厚的下圆盘Free layer-l具有较大的半径 r ~l~，1 nm厚的上圆盘Free layer-u具有较小的半径 r ~u~，这两自由层被中间1 nm厚的钌（Ru）层物理分隔开，于是便组成了一个非对称的SAFM结构。即Ruderman-Kittel-Kasuya-Yosida（RKKY）层间交换耦合只存在于layer-u和其下方layer-l的中心区域，而不会存在于layer-l余下的环形区域。layer-l和layer-u都被考虑为FM/HM双层结构，以便同时引入Dzyaloshinskii-Moriya相互作用（DMI）和垂直磁各向异性（PMA）。此外，考虑较厚的固定层Fixed layer持有径向涡旋状的磁化构型[92--95]，用于极化从半径为 r ~e~ 的顶电极注入的垂直电流。

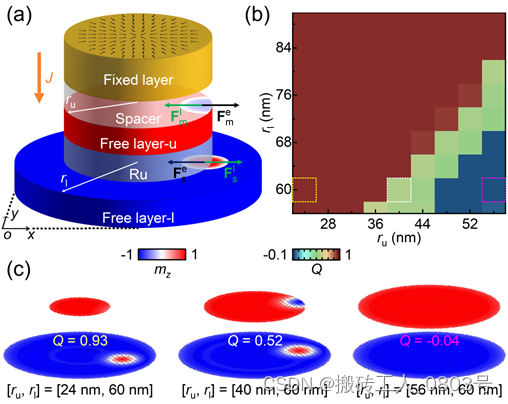
(a) 非对称SAFM圆盘，(b) Q 值关于两圆盘尺寸的相图，(c) 三种静态磁化构型

图4-1 器件结构和可能的磁化构型

我们使用OOMMF[101,112]来进行微磁模拟，也使用了带自定义场项的MuMax3[103]，以便检查模拟结果的可复现性，实际上二者的模拟结果并没有明显差异。在进行微磁模拟时，首先都是需要找到磁体系存在的静态磁化构型，接着便是通过求解Landau-Lifshitz-Gilbert-Slonczewski方程来追踪由电流驱动的磁化动力学[90,93]：
∂ m ∂ t = − γ ( m × H e f f ) + α ( m × ∂ m ∂ t ) + T s ( 4.1 ) \frac{\partial\mathbf{m}}{\partial{t}}=-\gamma\left(\mathbf{m}\times\mathbf{H}_{eff}\right)+\alpha\left(\mathbf{m}\times\frac{\partial\mathbf{m}}{\partial t}\right)+\mathbf{T}_s (4.1) ∂t∂m=−γ(m×Heff)+α(m×∂t∂m)+Ts(4.1) 其中 γ 是旋磁比，α 是吉尔伯特阻尼系数，t 是时间，H ~eff~ 是总的有效磁场，包含海森堡交换场、磁偶极场、垂直各向异性场、DMI有效场和层间交换有效场。 T s = γ B J ( m × p × m ) \mathbf{T}_s=\gamma B_J\left(\mathbf{m}\times\mathbf{p}\times\mathbf{m}\right) Ts=γBJ(m×p×m) 是自旋转移矩，其中极化方向呈径向涡旋状分布，即 p = ( c o s φ p , s i n φ p , 0 ) \mathbf{p}=\left(cos\varphi_p,\ \ sin\varphi_p,\ 0\right) p=(cosφp, sinφp, 0)， φ p = a r c t a n ( r l − y r l − x ) + φ \varphi_p=arctan\left(\frac{r_l-y}{r_l-x}\right)+\varphi φp=arctan(rl−xrl−y)+φ，其中 φ 为极化方向与径向方向之间的夹角[93]。Slonczewski转矩系数 B J = ℏ P J 2 e μ 0 M s t f B_J=\frac{\hbar P J}{2e\mu_0M_st_f} BJ=2eμ0MstfℏPJ 中的 ħ 是约化普朗克常量，P 是自旋极化率，J 是电流密度，e 是电子电荷，μ ~0~ 是真空磁导率，M ~s~ 是饱和磁化强度，自由层厚度 t ~f~ 等于1 nm。

我们选择的材料参数是Pt/Co多层膜的典型实验值[65,108,109]：饱和磁化强度 M ~s~ = 580 kA/m，交换系数 A = 15 pJ/m，PMA常数 K ~u~ = 0.8 MJ/m^3^，iDMI参数 D = 3.5 mJ/m^2^，阻尼系数 α = 0.02。此外，除非另有说明，那么层间交换相互作用的双线性界面交换系数默认为 σ = -2 mJ/m^2^（负值表示双层反铁磁耦合）[128]。考虑极化电流可以流入两自由层，并设置自旋极化率 P = 0.4。在所有模拟中，单元格尺寸都被设置为2 × 2 × 1 nm^3^。

4.2 麦纫-斯格明子对的稳定机制

一种生成MS pair的可行方案是在layer-u与layer-l的分界处注入一个局域的自旋极化电流，于是借助STT效应来翻转layer-l的局域磁化以用于使斯格明子成核，同时由于存在强烈的层间交换相互作用，在layer-u边缘处会立即镜像压印一个麦纫的成核位点[127]。在撤去外加激励并进行弛豫的过程中，麦纫会受到来自layer-u边缘向外的吸引力 F m e \ \mathbf{F}_m^e Fme 以及来自斯格明子向内的拖拽力 F m I \mathbf{F}_m^I FmI。同时，斯格明子会受到来自layer-l边缘向内的排斥力 F s e \mathbf{F}_s^e Fse 和来自麦纫向外的拖拽力 F s I \mathbf{F}_s^I FsI。

由于边缘对磁纹理的等效作用力对它们之间的相互距离非常敏感，所以考虑两圆盘的尺寸关系 r ~u~/r ~l~ 满足一定的范围时（例如，图4-1（b）中的白色虚线框标注），MS pair受到的合力便可以为0（即 F m e + F m I = 0 \mathbf{F}_m^e+\mathbf{F}_m^I=0 Fme+FmI=0， F s e + F s I = 0 \mathbf{F}_s^e+\mathbf{F}_s^I=0 Fse+FsI=0），使得层间耦合的MS pair能够稳定在layer-u的边缘。此时，磁体系的静态磁化构型如图4-1（c）中间面板所示，整个磁体系的拓扑电荷 Q ~ 0.5，这符合边缘麦纫（Q ~em~ = -0.5）和斯格明子（Q ~sk~ = +1）组合得到的预期拓扑电荷（Q = Q ~em~ + Q ~sk~）。

当考虑两圆盘的尺寸关系 r ~u~/r ~l~ 位于较小的范围时（例如，图4-1（b）中的黄色虚线框标注），由于注入的斯格明子距离layer-l的边缘较远，于是layer-l边缘作用在斯格明子身上向内的排斥力 F s e \mathbf{F}_s^e Fse 无法平衡layer-u边缘作用在麦纫身上向外的吸引力，于是麦纫便被layer-u排出来，同时斯格明子也会被拖向layer-l的边缘。最终，layer-l中的斯格明子会轻微变形并稳定在layer-u边缘与layer-l边缘之间的环形区域，这种钉扎现象是由于FM/SAFM混合结构的边界和layer-l边缘都存在势垒导致的[127,129]。此时，磁体系的静态磁化构型如图4-1（c）左面板所示，整个磁体系的拓扑电荷 Q ~ 1。然而，当两圆盘的尺寸关系 r ~u~/r ~l~ 位于较大的范围时（例如，图4-1（b）中的品红色虚线框标注），麦纫和斯格明子都会被排出，磁体系演变成反铁磁耦合的两个磁单畴，于是磁体系的拓扑电荷 Q ~ 0，如图4-1（c）右面板所示。需要注意的是，对于图4-1（b）中所考虑的两圆盘尺寸[r ~u~ , r ~l~]，在该相图中并没有出现斯格明子对SS pair（也称为双层斯格明子[65]），这是因为在形成斯格明子对的过程中需要麦纫克服很高的势垒来转化为斯格明子。相图中MS pair存在的狭窄区域则是源于斯格明子和layer-l边缘之间的等效相互作用力非常依赖于它们之间的相互距离。

4.3 麦纫-斯格明子对绕固定轨道旋转运动

之后的研究主要关注由垂直电流驱动的MS pair旋转动力学，除非另有说明，否则所有结果和讨论都是基于 [r ~u~ , r ~l~] = [40 nm, 60 nm] 和 r ~e~ = r ~u~ = 40 nm的STNO。当从顶电极注入 J = 1.5×10^11^ A/m^2^的电流时，固定层会将其转变为具有径向涡旋状极化方向的极化电流，接着极化电流同时对layer-u和layer-l的局域磁矩施加自旋转移矩。电流驱动MS pair的磁化快照如图4-2（a）所示，可以看到麦纫和斯格明子利用层间交换相互作用绑定在一起，并且沿layer-u的边缘同步顺时针旋转，图中黄色符号标注的区域（Detection area）表示基于磁电阻效应的麦纫检测设备的位置。

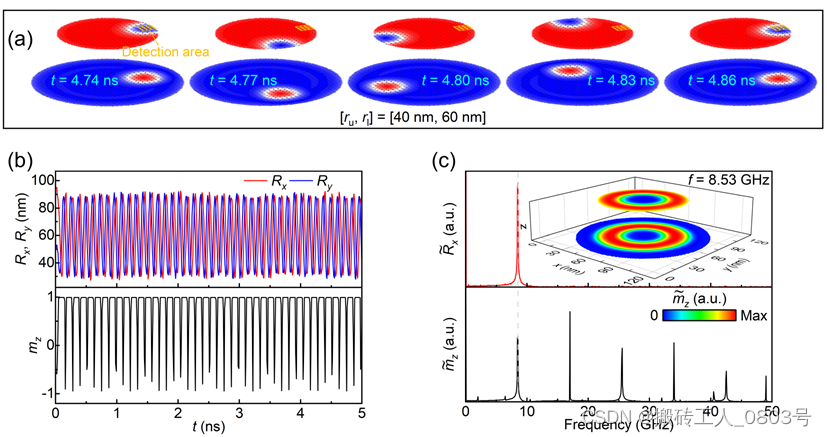
(a) 在给定电流密度下MS pair顺时针旋转，(b) MS pair的运动轨迹和检测单元采样的信号，(c) FFT频谱以及相应频率的模式分布

图4-2 MS pair的频率特性

我们使用Python程序获取按等时间间隔保存的磁化文件中MS pair的空间位置[130]，图4-2（b）给出了MS pair的运动轨迹 (R ~x~, R ~y~) 和检测区域内的平均磁化分量 m ~z~ 随时间的振荡曲线，可以看到在施加电流后，MS pair会立即进入固定的圆周轨道并进行稳定的旋转运动，因此STNO的启动时间会非常小。图4-2（c）是 R ~x~ 和 m ~z~ 的快速傅里叶变换（FFT）频谱，这表明MS pair在注入电流 J = 1.5×10^11^ A/m^2^时的旋转频率为8.53 GHz（也即STNO的实际输出频率）。在图4-2（c）的内部插图中显示了该频率的模式分布，这可以用于辅助识别MS pair的运动轨迹。需要注意的是，虽然 R ~x~ 和 m ~z~ 拥有着相同的振荡周期，但是 m ~z~ 随时间的振荡曲线 m ~z~(t) 并不是纯粹的正弦波形，所以其频谱中出现了许多的等间隔分布的高次谐波[131]。

4.4 几何参数和磁性参数对振荡器输出频率的影响

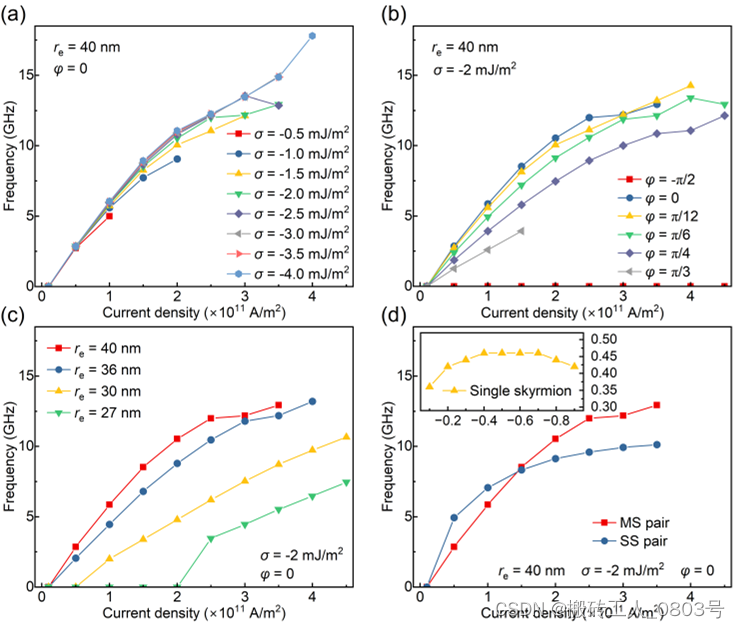
(a) 调节层间交换耦合系数，(b) 调节极化角，(c) 调节电极尺寸，(d) 调节上圆盘尺寸

图4-3 STNO的频谱特性

接着我们分析了影响STNO输出频率的因素，结果表明其输出频率不仅随电流密度而变化，还依赖于自身的几何参数和磁性参数。图4-3（a）表示维持 φ = 0并调节耦合系数 σ ，以用于分析STNO输出频率对电流密度的依赖关系 f (J )。可以看到对于每个耦合系数 σ ，STNO都有一个相应的最大电流密度，即倘若超过该最大电流密度，麦纫和斯格明子将不再紧密耦合导致MS pair存在着湮灭的风险，以至于使STNO失去功能。然而当层间交换作用足够强后，调节耦合系数 σ 对STNO在给定电流密度下的输出频率不会产生明显的影响。然而，如图4-3（b）所示，极化角 φ 可以显著地影响STNO的输出频率。具体而言，STNO关于极化角 φ 的最大电流密度是非单调变化的，特别是当 φ 增加到π/3时，STNO的最大电流密度急剧降低。图4-3（c）中展示了 φ = 0且在相同的电流密度情况下，顶电极尺寸半径 r ~e~ 对STNO输出频率的影响，可以看到较小的电极尺寸会降低STNO的输出频率并提高MS pair起振的阈值电流密度。

为了与其他类型STNO的输出频率进行比较，只需要对所原来的模型稍作调整，便可模拟基于斯格明子对的STNO。即将layer-u和layer-l的尺寸设为相同（r ~u~ = r ~l~ = 60 nm），于是STNO就变成了对称的SAFM纳米圆盘结构[65,95]。同样的，该类型STNO的输出频率实际取决于斯格明子对的旋转频率。当注入合适的电流时，斯格明子对也是顺时针旋转，但其旋转轨道随注入电流而变化。如图4-3（d）所示，斯格明子对的旋转频率在较小电流密度下高于MS pair，但随着电流密度的增加，斯格明子对旋转频率的增长逐渐放缓，最终被MS pair反超。除此以外，我们也模拟了基于单层斯格明子的STNO，即考虑不存在layer-u和Ru层的情况下（r ~u~ = 0 nm），使用电流驱动在layer-l中的斯格明子。模拟结果如图4-3（d）中插图所示，该斯格明子只有在合适的负电流密度下才能逆时针旋转，但其旋转频率仅有数百MHz。然而当电流密度为正时，斯格明子将沿顺时针方向回到圆盘中心[92,93]。

(a) 斯格明子对的旋转频率为4.86 GHz，(b) 单层斯格明子的旋转频率为0.43 GHz

图4-4 斯格明子对和单层斯格明子的模式分布

图4-4（a）和（b）分别展示斯格明子对和单层斯格明子在特定旋转频率下相应的模式分布，其中斯格明子对在电流密度为 J = 0.5×10^11^ A/m^2^ 时的旋转频率为4.86 GHz，然而单层斯格明子在电流密度为J = -0.5×10^11^ A/m^2^ 时的旋转频率仅有0.43 GHz。

4.5 Thiele方程分析麦纫-斯格明子对动力学

为了深入理解麦纫和斯格明子实现同步旋转背后的机理，需要分析单层极化电流对相应磁纹理的作用效果。我们在模拟中设置极化电流分别仅存在于layer-u或layer-l，并且电极尺寸固定为 r ~e~ = 40 nm。模拟结果如图4-5（b）所示，MS pair在任一层极化电流下都能顺时针旋转，这暗含了极化电流对麦纫和斯格明子的驱动力必须是同向的。然而无论是MS pair还是斯格明子对，使用单层极化电流都会使它们的旋转频率降低，这意味着为了提高STNO的输出频率，最好是使用双层极化电流。

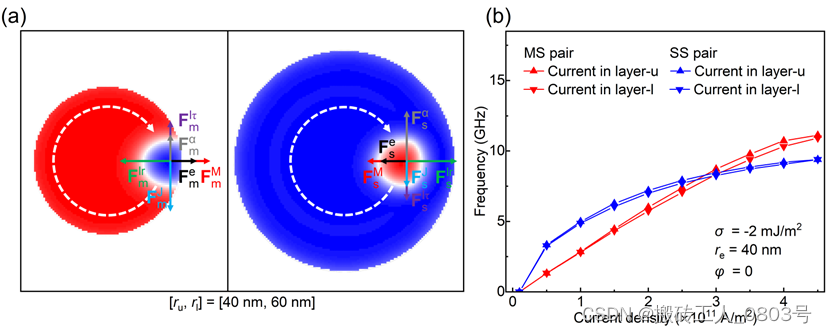
(a) MS pair受到的等效作用力，(b) 单层极化电流下的旋转频率

图4-5 MS pair受力示意图和层间交换耦合辅助的运动

电流驱动MS pair的旋转运动可以用Thiele方程来描述[92--95,129]，对于麦纫来说：
F m M + F m e + F m I + F m α + F m J = 0 ( 4.2 ) \mathbf{F}_m^M+\mathbf{F}_m^e+\mathbf{F}_m^I+\mathbf{F}_m^\alpha+\mathbf{F}_m^J=0 (4.2) FmM+Fme+FmI+Fmα+FmJ=0(4.2)

对于斯格明子来说：
F s M + F s e + F s I + F s α + F s J = 0 ( 4.3 ) \mathbf{F}s^M+\mathbf{F}s^e+\mathbf{F}s^I+\mathbf{F}s^\alpha+\mathbf{F}s^J=0 (4.3) FsM+Fse+FsI+Fsα+FsJ=0(4.3) 式中从左往右分别表示马格纳斯力、边缘诱导的力、麦纫和斯格明子的相互作用的内力、耗散力以及电流的驱动力，这些等效作用力的方向如图4-5（a）所示。马格纳斯力 F M = C G × v \mathbf{F}^M=C\mathbf{G}\times\mathbf{v} FM=CG×v，其系数 C = μ 0 M s t f / γ C=\mu_0M_st_f/\gamma C=μ0Mstf/γ 取决于材料参数， v \mathbf{v} v 表示MS pair的切向速度，旋磁矢量 G = 4 π Q z ^ \mathbf{G}=4\pi Q\hat{z} G=4πQz^ ， z ^ \mathbf{ẑ} z^ 表示 +z 方向的单位矢量。边缘诱导的力 F e = − ∇ U \mathbf{F}^e=-\nabla{U} Fe=−∇U，其中 U 是势能函数。耗散力 F α = α C D ↔ ⋅ v \mathbf{F}^\alpha=\alpha C\overleftrightarrow{\mathcal{D}}\cdot\mathbf{v} Fα=αCD ⋅v，其中 D ↔ = ( D x x D x y D y x D y y ) \overleftrightarrow{\mathcal{D}}=\begin{pmatrix} \mathcal{D}{xx} & \mathcal{D}{xy} \\ \mathcal{D}{yx} & \mathcal{D}{yy} \end{pmatrix} D =(DxxDyxDxyDyy) 并且有： D x x = ∫ d x d y ( ∂ m ∂ x ⋅ ∂ m ∂ x ) \mathcal{D}{xx}=\int dxdy\left(\frac{\partial\mathbf{m}}{\partial x}\cdot\frac{\partial\mathbf{m}}{\partial x}\right) Dxx=∫dxdy(∂x∂m⋅∂x∂m)， D y y = ∫ d x d y ( ∂ m ∂ y ⋅ ∂ m ∂ y ) \mathcal{D}{yy}=\int dxdy\left(\frac{\partial\mathbf{m}}{\partial y}\cdot\frac{\partial\mathbf{m}}{\partial y}\right) Dyy=∫dxdy(∂y∂m⋅∂y∂m)， D x y = ∫ d x d y ( ∂ m ∂ x ⋅ ∂ m ∂ y ) \mathcal{D}{xy}=\int dxdy\left(\frac{\partial\mathbf{m}}{\partial x}\cdot\frac{\partial\mathbf{m}}{\partial y}\right) Dxy=∫dxdy(∂x∂m⋅∂y∂m) 和 D y x = ∫ d x d y ( ∂ m ∂ y ⋅ ∂ m ∂ x ) \mathcal{D}_{yx}=\int dxdy\left(\frac{\partial\mathbf{m}}{\partial y}\cdot\frac{\partial\mathbf{m}}{\partial x}\right) Dyx=∫dxdy(∂y∂m⋅∂x∂m)。电流的驱动力 F J = F J r e ^ r + F J τ e ^ τ \mathbf{F}^J=F^{Jr}{\hat{e}}r+F^{J\tau}{\hat{e}}\tau FJ=FJre^r+FJτe^τ 可以被分解到径向方向和切向方向，其中 F J j = γ C B J S j F^{Jj}=\gamma C{B_J}S_j FJj=γCBJSj， S j = ∫ d x d y ( ( m × p ) ⋅ ∂ m ∂ j ) S_j=\int dxdy\left(\left(\mathbf{m}\times\mathbf{p}\right)\cdot\frac{\partial\mathbf{m}}{\partial j}\right) Sj=∫dxdy((m×p)⋅∂j∂m)，下标 j = ( r , τ ) j = (r, τ) j=(r,τ) 则表示径向方向和切向方向。麦纫和斯格明子相互作用的内力 F I = F I r e ^ r + F I τ e ^ τ \mathbf{F}^I=F^{Ir}{\hat{e}}r+F^{I\tau}{\hat{e}}\tau FI=FIre^r+FIτe^τ 则是源于层间交换作用。

将式子（4.2）和（4.3）相加，我们可以得到描述MS pair稳定运动的Thiele方程： F M + F e + F α + F J = 0 \mathbf{F}^M+\mathbf{F}^e+\mathbf{F}^\alpha+\mathbf{F}^J=0 FM+Fe+Fα+FJ=0， F I \mathbf{F}^I FI 作为内力则被忽略。在MS pair处于稳定的圆周运动过程中，由于其径向速度为零，所以MS pair的净速度 v = v e ^ τ {\mathbf{v}=v\hat{e}}\tau v=ve^τ 可以从切向方向的Thiele方程 F α τ e ^ τ + F J τ e ^ τ = 0 F^{\alpha\tau}{\hat{e}}\tau+F^{J\tau}{\hat{e}}\tau=0 Fατe^τ+FJτe^τ=0 中推导出来，即满足： α C D y y v e ^ τ − γ C B J S τ e ^ τ = 0 \alpha C\mathcal{D}{yy}v{\hat{e}}\tau-\gamma CB_JS\tau{\hat{e}}\tau=0 αCDyyve^τ−γCBJSτe^τ=0。于是，倘若能求解 D x y \mathcal{D}{xy} Dxy， D y y \mathcal{D}{yy} Dyy， S r S_r Sr 和 S τ S\tau Sτ，那么便可以将耗散力的径向分量 F α r = α C D x y v F^{\alpha r}=\alpha C\mathcal{D}{xy}v Fαr=αCDxyv 和电流驱动力的径向分量 F J r = γ C B J S r F^{Jr}=\gamma CB_JS_r FJr=γCBJSr 计算出来。如图4-5（a）所示，为了简化计算，此处考虑MS pair顺时针运动至圆周轨道的右端点，于是MS pair的速度就仅指向 -y 方向。此外，我们使用符号标记式子为： D y y = D = ∫ d x d y ( ∂ m ∂ y ⋅ ∂ m ∂ y ) {\mathcal{D}{yy}}=\mathcal{D}=\int dxdy\left(\frac{\partial\mathbf{m}}{\partial y}\cdot\frac{\partial\mathbf{m}}{\partial y}\right) Dyy=D=∫dxdy(∂y∂m⋅∂y∂m)， S τ = S = ∫ d x d y ( ( m × p ) ⋅ ∂ m ∂ y ) S_\tau=S=\int dxdy\left(\left(\mathbf{m}\times\mathbf{p}\right)\cdot\frac{\partial\mathbf{m}}{\partial y}\right) Sτ=S=∫dxdy((m×p)⋅∂y∂m)，以及 D x y = D ′ = ∫ d x d y ( ∂ m ∂ x ⋅ ∂ m ∂ y ) \mathcal{D}_{xy}=\mathcal{D}\prime=\int dxdy\left(\frac{\partial\mathbf{m}}{\partial x}\cdot\frac{\partial\mathbf{m}}{\partial y}\right) Dxy=D′=∫dxdy(∂x∂m⋅∂y∂m)， S r = S ′ = ∫ d x d y ( ( m × p ) ⋅ ∂ m ∂ x ) S_r=S\prime=\int dxdy\left(\left(\mathbf{m}\times\mathbf{p}\right)\cdot\frac{\partial\mathbf{m}}{\partial x}\right) Sr=S′=∫dxdy((m×p)⋅∂x∂m)。

倘若能知道 m (x , y ) 的显式表达式，那么便能计算 D \mathcal{D} D， S S S， D ′ \mathcal{D}\prime D′ 和 S ′ S\prime S′。实际上，虽然已经有不只一种表达式能描述斯格明子的磁化分布[109,132,133]，但目前并没有相关的表达式来描述边缘麦纫的磁化分布。尽管如此，我们仍然可以基于模拟输出的磁化文件来对 D \mathcal{D} D， S S S， D ′ \mathcal{D}\prime D′ 和 S ′ S\prime S′ 进行数值求解。考虑 ∂ m ∂ x \frac{\partial\mathbf{m}}{\partial x} ∂x∂m 和 ∂ m ∂ y \frac{\partial\mathbf{m}}{\partial y} ∂y∂m 的离散形式： ∂ m ∂ x → ∆ m ∆ x = m ( x + ∆ x ) − m ( x − ∆ x ) 2 ∆ x \frac{\partial\mathbf{m}}{\partial x}\rightarrow\frac{∆\mathbf{m}}{∆x}=\frac{\mathbf{m}(x+∆x)-\mathbf{m}(x-∆x)}{2∆x} ∂x∂m→∆x∆m=2∆xm(x+∆x)−m(x−∆x) 以及 ∂ m ∂ y → ∆ m ∆ y = m ( y + ∆ y ) − m ( y − ∆ y ) 2 ∆ y \frac{\partial\mathbf{m}}{\partial y}\rightarrow\frac{∆\mathbf{m}}{∆y}=\frac{\mathbf{m}(y+∆y)-\mathbf{m}(y-∆y)}{2∆y} ∂y∂m→∆y∆m=2∆ym(y+∆y)−m(y−∆y)，于是使用一些Python程序[130]，我们便为麦纫和斯格明子计算出了各自的 D \mathcal{D} D， S S S， D ′ \mathcal{D}\prime D′ 和 S ′ S\prime S′。

例如，在电流密度 J = 5×10^10^ A/m^2^ 下的MS pair，对于麦纫来说： D m = 95.0 \mathcal{D}_m = 95.0 Dm=95.0， S m = 93.9 n m S_m = 93.9\ nm Sm=93.9 nm。对于斯格明子则有： D s = 172.3 \mathcal{D}_s = 172.3 Ds=172.3， S s = 96.7 n m S_s = 96.7\ nm Ss=96.7 nm。然而，在我们所考虑的电流密度范围内，麦纫和斯格明子的 D ′ \mathcal{D}\prime D′ 和 S ′ S\prime S′ 总是很小（ ∣ D ′ ∣ < 2.5 |\mathcal{D}′| < 2.5 ∣D′∣<2.5， ∣ S ′ ∣ < 10 n m |\mathcal{S}′| < 10\ nm ∣S′∣<10 nm），因此我们在图4-5（a）中省略了耗散力的径向分量和电流驱动力的径向分量。

有了这些数值解，于是就可以很容易得到MS pair的（切向）速度，即 v = γ S p α D p B J e ^ τ \mathbf{v}=\frac{\gamma S_p}{\alpha\mathcal{D}p}B_J{\hat{e}}\tau v=αDpγSpBJe^τ，其中 D p = D m + D s \mathcal{D}_p = \mathcal{D}_m + \mathcal{D}_s Dp=Dm+Ds， S p = S m + S s S_p = S_m + S_s Sp=Sm+Ss。我们计算的 D \mathcal{D} D 和 S S S 的数值解对电流密度的依赖关系如图4-6所示，注意我们总是选取磁纹理旋转运动到圆周轨道的右端点进行分析。从图4-6（a）和（b）中MS pair的数据来看，麦纫的 D \mathcal{D} D 值远小于斯格明子的 D \mathcal{D} D 值，但二者的 S S S 值却几乎相等。此外，在所有情况中， S S S 都要比 D \mathcal{D} D 对电流密度更敏感。具体而言，MS pair的 S S S 值随着电流密度的增加而增加，而对于斯格明子对和单层斯格明子来说， S S S 值则是随着电流密度的增加而减小。这些因素会导致一个可预期的结果，即在足够高的电流密度下，MS pair比斯格明子对运动得更快因而具有更高的旋转频率。此外，当考虑相同强度的电流密度时，单层斯格明子的 S S S 值远小于MS pair和斯格明子对，这导致了另一个可预期的结果，即单层斯格明子的旋转频率相对较低[90,93]。

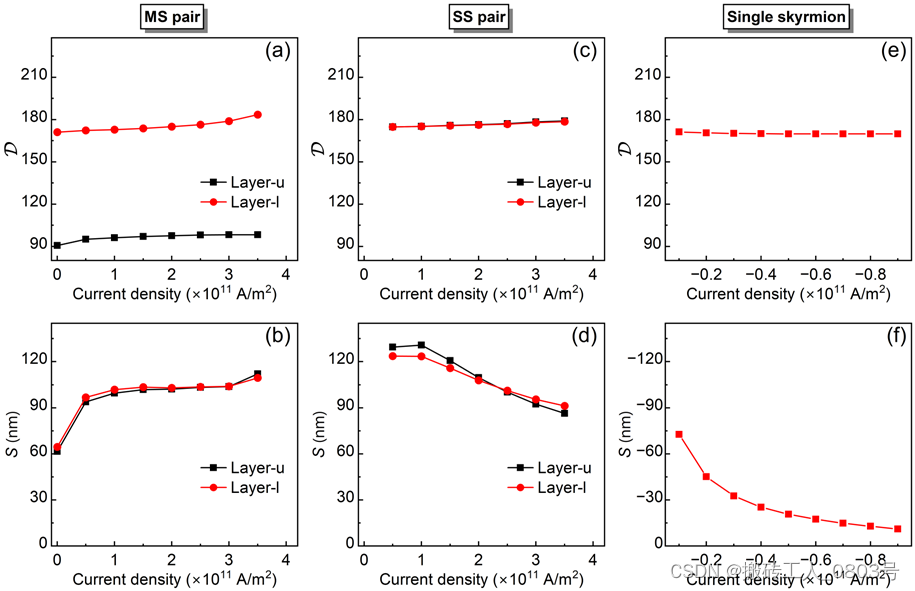
(a) 和 (b) MS pair，(c) 和 (d) 斯格明子对，(e) 和 (f) 单层斯格明子

图4-6 不同磁纹理的 D \mathcal{D} D 和 S S S 对电流密度的依赖关系

4.6 多个麦纫-斯格明子对提升振荡器输出频率

基于斯格明子的STNO可以通过在单个纳米圆盘中放置多个斯格明子进行同步旋转，从而显著提高其实际输出频率[90,95]。基于该思路，如图4-7（a）所示，我们也往单个STNO中放置了中心对称分布的多个MS pair（N = 2，3，4，5），并分析电流驱动多个MS pair的旋转动力学。实际上，对于仅持有一个MS pair的STNO，其输出频率显然等于MS pair的旋转频率。然而，倘若STNO持有多个同步旋转的MS pair，那么检测装置能在相同的时间内检测到更多的MS pair，于是STNO此时的输出频率大致等于单个MS pair的旋转频率乘以MS pair的数量。正如图4-7（b）所示，STNO的输出频率随着MS pair数量的增加而增加。需要注意的是，如果注入过大的电流，MS pair的对称分布将被破坏，并且MS pair之间复杂的相互作用将导致一些MS pair变形和湮灭，从而使STNO输出与预期不符的频率。

通常，基于斯格明子或MS pair的STNO很难输出纯粹的正弦信号，这是因为基于磁电阻效应的检测装置只能记录斯格明子或MS pair的存在而无法实时追踪它们的运动轨迹。但是，当STNO持有多个MS pair的情况下，这个问题可以得到改善。STNO持有两个和五个MS pair时的频谱与电流密度的依赖关系分别如图4-7（c）和（d）所示，可以看到高次谐波的强度随着MS pair数量的增加而显著降低，这主要归功于检测装置检测到MS pair的间隔时间减少。

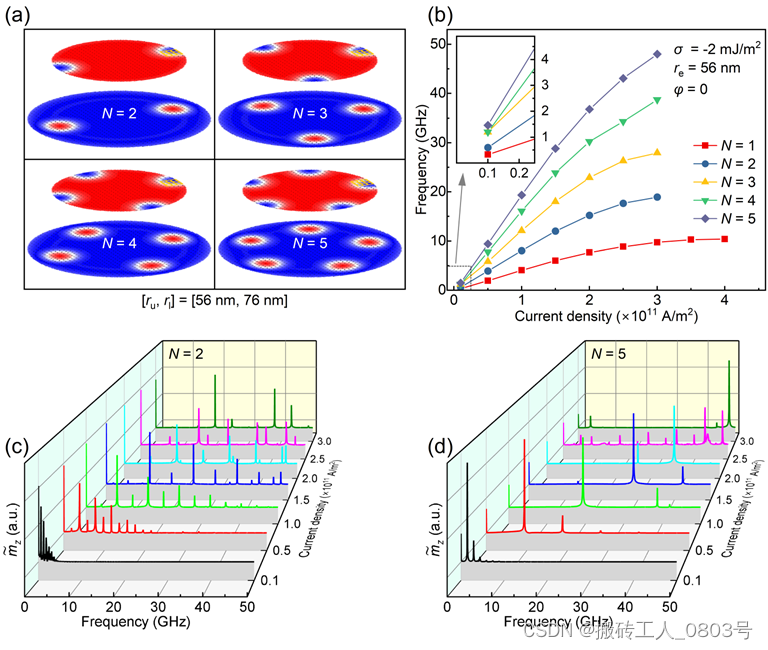
(a) 中心对称分布的多个MS pair，(b) STNO的实际输出频率，(c) STNO持有两个MS pair时的频谱特性，(d) STNO持有五个MS pair时的频谱特性

图4-7 持有多个MS pair的单个STNO的频谱特性

4.7 弱无序性参数对麦纫-斯格明子对动力学的影响

对于基于斯格明子的STNO来说，样品中存在的弱无序性材料参数可能会对斯格明子的旋转轨道造成扰动，这会增加频谱中的噪声分量[93]，这促使我们测试弱无序性参数对MS pair动力学的影响。考虑真实样品中存在的晶粒会导致PMA常数的随机变化ΔK ~u~，于是我们使用Voronoi tessellation生成了两种晶粒图案：（1）设置平均晶粒尺寸为10 nm，以及晶粒中的PMA强度在5%以内随机增减，如图4-8（a）所示。（2）设置平均晶粒尺寸为25 nm，以及晶粒中的PMA强度在2%以内随机增减，如图4-8（b）所示。

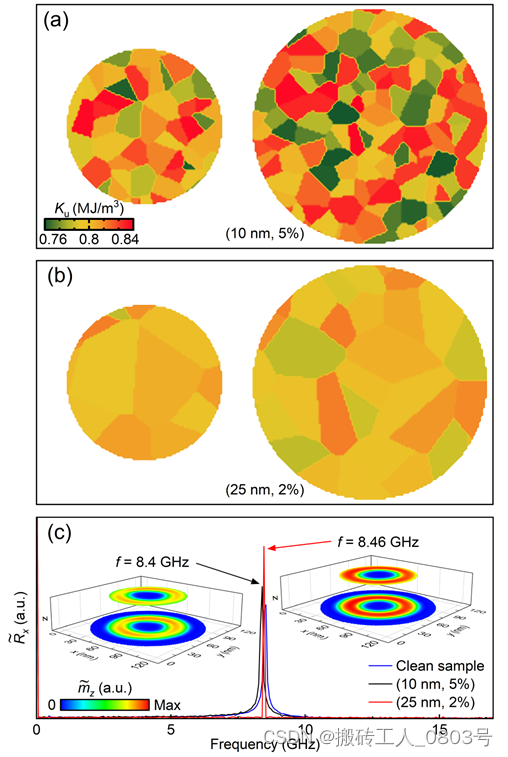
(a) 10 nm的平均晶粒尺寸和晶粒内的PMA在5%以内随机变化，(b) 25 nm的平均晶粒尺寸和晶粒内的PMA在2%以内随机变化，(c) MS pair的频率特性和相应频率的模式分布

图4-8 无序性材料参数对MS pair特性的影响

图4-8（c）中考虑驱动MS pair的电流密度为 J = 1.5×10^11^ A/m^2^，作为参考的蓝色曲线是图4-2中描述的设置均匀PMA强度时的频谱。从频谱和相应频率的模式分布中可以看出，PMA强度的随机变化仅仅使MS pair的旋转速度受到扰动，但不影响MS pair围绕固定的圆周轨道旋转。此外，MS pair的旋转频率随着平均晶粒尺寸的变化而呈现非单调的变化，且三种情况下的频率线宽（full width at half maximum of the peak）均小于116MHz。

第五章结论与展望

5.1 总结

本文的研究内容围绕磁畴壁、边缘麦纫和斯格明子等磁纹理而展开，所谓的磁化动力学囊括了磁矩小幅度的进动以及大幅度的翻转。我们的研究表明，通过巧妙地组合多个磁纹理并合理地利用它们之间的相互作用，可以为一些关键技术瓶颈的突破提供可行的思路。具体的研究内容主要如下：

（1）系统性地总结了与本课题相关的中外文献。在充分了解国内外有关研究磁振子晶体以及自旋转矩纳米振荡器的基础上，发现兼容磁畴壁波导的磁振子晶体的相关研究还存在空白，并且传统的基于磁斯格明子的STNO还存在一些固有缺点亟待解决。基于这些问题，本文深入探索了畴壁波导的能带结构调控手段，以及将STNO中混合磁纹理的旋转轨道固定的方法。

（2）理论提出并通过微磁模拟验证了利用偶极耦合的array-on-film铁磁双层结构来调控磁畴壁波导的能带结构。首先分析了该array-on-film磁体系可能存在的四种静态磁化构型：Loop、C-C、C-up和C-down，以及它们各自的磁矩排列特征。然后通过对比分析独立畴壁波导无带隙的频率谱和色散关系，发现了当磁体系处于具有磁通闭合特征的Loop构型时，一些带隙会在畴壁波导的能带中打开。接着为了探索带隙打开的起源，系统地研究了条带阵列的静态杂散场和动态杂散场分别对带隙打开的贡献。研究结果表明，条带阵列静态杂散场的耦合会在畴壁波导中诱导出周期势场，当束缚态自旋波满足布拉格反射条件时，带隙便会出现在布里渊区边界处。此外，当考虑动态杂散场的耦合时，我们认为畴壁波导中处于带隙内的束缚态自旋波若是满足模式匹配的条件，则可以和条带阵列中的束缚态自旋波诱导出共振增强的集体传播模式，以用于辅助带隙内的束缚态自旋波穿过周期势场，从而在带隙内形成狭窄允带。最后，详细地分析了由几何结构决定的固定周期参数以及由磁化构型控制的可重构周期参数对能带结构的影响。这些结果表明，我们所设计的磁振子晶体具有可重构能带结构的特性，并且存在众多的调控手段以及兼容广泛的应用场景。

（3）设计了一种具有非对称SAFM纳米圆盘结构的STNO，并研究了MS pair在该磁体系中的旋转动力学。首先，通过微磁模拟分析了边缘麦纫和斯格明子分别受到的等效作用力，进而唯象地解释了MS pair磁化构型的稳定机制。其次，模拟结果表明STNO通入工作电流后，MS pair可以围绕固定的圆周轨道旋转，于是STNO便能输出稳定的周期信号。此外，STNO的输出频率不仅依赖电流密度大小，还受几何参数和磁性参数影响。接着借助Thiele模型描述了MS pair的旋转动力学，解释了MS pair的旋转频率高于斯格明子对和单层斯格明子的原因。最后，单个STNO中的多个MS pair同步旋转可以将STNO的输出频率进一步提高，以及弱无序性材料参数的存在不会显著改变STNO的关键特征。这些结果表明，本文提出的基于MS pair的STNO有望解决基于磁斯格明子的STNO存在的启动时间长，旋转轨道随电流变化等固有问题。

5.2 展望

虽然本文为调控畴壁波导的能带提供了一种思路，但是可以预想未来还存在其他方式来调控畴壁波导的能带，比如使用压控各向异性单元组成的阵列来实现磁晶各向异性的周期变化。此外，针对本文所设计的Loop、C-C、C-up、C-down磁化构型，目前在实验上还缺乏能使磁体系在这些磁化构型之间灵活切换的手段。

本文在设计具有固定轨道的STNO时，关于所提出的MS pair还缺乏相关的实验证据能验证其存在，可以预想未来能提出一种实验上可行的MS pair生成方法。

本文通过组合磁纹理来实现了一些特殊的功能：通过组合多个周期排列的磁畴壁实现了对畴壁波导的能带调控，通过组合麦纫和斯格明子实现了磁纹理运动轨道的固定。除此以外，磁体系中丰富的相互作用还孕育出其他各具特色的磁纹理，可以预想未来能够实现更多的磁纹理组合以用于解决单个磁纹理所面临的瓶颈问题。

参考文献

[1] Žutić I, Fabian J, Das Sarma S. Spintronics: Fundamentals and applications[J]. Reviews of Modern Physics, 2004, 76(2): 323-410.

[2] Grünberg P, Schreiber R, Pang Y, et al. Layered magnetic structures: Evidence for antiferromagnetic coupling of Fe layers across Cr interlayers[J]. Physical Review Letters, 1986, 57(19): 2442-2445.

[3] Baibich M N, Broto J M, Fert A, et al. Giant magnetoresistance of (001)Fe/(001)Cr magnetic superlattices[J]. Physical Review Letters, 1988, 61(21): 2472-2475.

[4] Piramanayagam S N. Perpendicular recording media for hard disk drives[J]. Journal of Applied Physics, 2007, 102(1): 011301.

[5] Parkin S, Yang S H. Memory on the racetrack[J]. Nature Nanotechnology, 2015, 10(3): 195-198.

[6] Julliere M. Tunneling between ferromagnetic films[J]. Physics Letters A, 1975, 54(3): 225-226.

[7] Slonczewski J C. Current-driven excitation of magnetic multilayers[J]. Journal of Magnetism and Magnetic Materials, 1996, 159(1-2): L1-L7.

[8] Berger L. Emission of spin waves by a magnetic multilayer traversed by a current[J]. Physical Review B, 1996, 54(13): 9353-9358.

[9] Zhang S, Li Z. Roles of nonequilibrium conduction electrons on the magnetization dynamics of ferromagnets[J]. Physical Review Letters, 2004, 93(12): 127204.

[10] Haazen P P J, Murè E, Franken J H, et al. Domain wall depinning governed by the spin Hall effect[J]. Nature Materials, 2013, 12(4): 299-303.

[11] Khvalkovskiy A V, Cros V, Apalkov D, et al. Matching domain-wall configuration and spin-orbit torques for efficient domain-wall motion[J]. Physical Review B, 2013, 87(2): 020402.

[12] 姜寿亭. 凝聚态磁性物理[M]. 科学出版社, 2003.

[13] Duine R A, Lee K J, Parkin S S P, et al. Synthetic antiferromagnetic spintronics[J]. Nature Physics, 2018, 14(3): 217-219.

[14] Wang K, Bheemarasetty V, Xiao G. Spin textures in synthetic antiferromagnets: Challenges, opportunities, and future directions[J]. APL Materials, 2023, 11(7): 070902.

[15] Heisenberg W. Zur Theorie des Ferromagnetismus[J]. Zeitschrift für Physik, 1928, 49(9): 619-636.

[16] Mahmoud A, Ciubotaru F, Vanderveken F, et al. Introduction to spin wave computing[J]. Journal of Applied Physics, 2020, 128(16): 161101.

[17] Au Y, Dvornik M, Dmytriiev O, et al. Nanoscale spin wave valve and phase shifter[J]. Applied Physics Letters, 2012, 100(17): 172408.

[18] Zheng L, Zhang D, Jin L, et al. Phase shifter and broadband XOR logic gate based on edge-mode--type spin wave in the waveguide[J]. EPL (Europhysics Letters), 2021, 134(3): 37003.

[19] Chen X, Wang Q, Liao Y, et al. Control phase shift of spin-wave by spin-polarized current and its application in logic gates[J]. Journal of Magnetism and Magnetic Materials, 2015, 394: 67-69.

[20] Zhang Z, Liu S, Wen T, et al. Bias-free reconfigurable magnonic phase shifter based on a spin-current controlled ferromagnetic resonator[J]. Journal of Physics D: Applied Physics, 2020, 53(10): 105002.

[21] Hämäläinen S J, Madami M, Qin H, et al. Control of spin-wave transmission by a programmable domain wall[J]. Nature Communications, 2018, 9(1): 4853.

[22] Vogt K, Fradin F Y, Pearson J E, et al. Realization of a spin-wave multiplexer[J]. Nature Communications, 2014, 5(1): 3727.

[23] Vogt K, Schultheiss H, Jain S, et al. Spin waves turning a corner[J]. Applied Physics Letters, 2012, 101(4): 042410.

[24] Ren Z, Liu S, Jin L, et al. Reconfigurable nanoscale spin-wave directional coupler using spin-orbit torque[J]. Scientific Reports, 2019, 9(1): 7093.

[25] Szulc K, Graczyk P, Mruczkiewicz M, et al. Spin-wave diode and circulator based on unidirectional coupling[J]. Physical Review Applied, 2020, 14(3): 034063.

[26] Seo S M, Lee K J, Yang H, et al. Current-induced control of spin-wave attenuation[J]. Physical Review Letters, 2009, 102(14): 147202.

[27] Woo S, Beach G S D. Control of propagating spin-wave attenuation by the spin-Hall effect[J]. Journal of Applied Physics, 2017, 122(9): 093901.

[28] Garcia-Sanchez F, Borys P, Soucaille R, et al. Narrow magnonic waveguides based on domain walls[J]. Physical Review Letters, 2015, 114(24): 247206.

[29] Xing X, Zhou Y. Fiber optics for spin waves[J]. NPG Asia Materials, 2016, 8(3): e246-e246.

[30] Lan J, Yu W, Wu R, et al. Spin-wave diode[J]. Physical Review X, 2015, 5(4): 041049.

[31] Wagner K, Kákay A, Schultheiss K, et al. Magnetic domain walls as reconfigurable spin-wave nanochannels[J]. Nature Nanotechnology, 2016, 11(5): 432-436.

[32] Albisetti E, Petti D, Sala G, et al. Nanoscale spin-wave circuits based on engineered reconfigurable spin-textures[J]. Communications Physics, 2018, 1(1): 56.

[33] Sluka V, Schneider T, Gallardo R A, et al. Emission and propagation of 1D and 2D spin waves with nanoscale wavelengths in anisotropic spin textures[J]. Nature Nanotechnology, 2019, 14(4): 328-333.

[34] Chang L J, Chen J, Qu D, et al. Spin wave injection and propagation in a magnetic nanochannel from a vortex core[J]. Nano Letters, 2020, 20(5): 3140-3146.

[35] Yu H, Xiao J, Schultheiss H. Magnetic texture based magnonics[J]. Physics Reports, 2021, 905: 1-59.

[36] Xing X, Pong P W T, Åkerman J, et al. Paving spin-wave fibers in magnonic nanocircuits using spin-orbit torque[J]. Physical Review Applied, 2017, 7(5): 054016.

[37] Zhang B, Wang Z, Cao Y, et al. Eavesdropping on spin waves inside the domain-wall nanochannel via three-magnon processes[J]. Physical Review B, 2018, 97(9): 094421.

[38] Xing X, Wang T, Zhou Y. Amplifying spin waves along Néel domain wall by spin--orbit torque[J]. Applied Physics Letters, 2021, 118(6): 062405.

[39] Yu H, Ma X P, Zhang H, et al. Magnon-bandgap controllable artificial domain wall waveguide[J]. Applied Physics Letters, 2023, 122(24): 242403.

[40] Krawczyk M, Grundler D. Review and prospects of magnonic crystals and devices with reprogrammable band structure[J]. Journal of Physics: Condensed Matter, 2014, 26(12): 123202.

[41] 张天蓉. 《硅火燎原》-9-布洛赫波和布里渊区[EB]//https://blog.sciencenet.cn/blog-677221-703395.html.

[42] Chumak A V, Serga A A, Hillebrands B. Magnonic crystals for data processing[J]. Journal of Physics D: Applied Physics, 2017, 50(24): 244001.

[43] Frey P, Nikitin A A, Bozhko D A, et al. Reflection-less width-modulated magnonic crystal[J]. Communications Physics, 2020, 3(1): 17.

[44] Gubbiotti G, Tacchi S, Carlotti G, et al. Collective spin modes in monodimensional magnonic crystals consisting of dipolarly coupled nanowires[J]. Applied Physics Letters, 2007, 90(9): 092503.

[45] Lee K S, Han D S, Kim S K. Physical origin and generic control of magnonic band gaps of dipole-exchange spin waves in width-modulated nanostrip waveguides[J]. Physical Review Letters, 2009, 102(12): 127202.

[46] Kim S K, Lee K S, Han D S. A gigahertz-range spin-wave filter composed of width-modulated nanostrip magnonic-crystal waveguides[J]. Applied Physics Letters, 2009, 95(8): 082507.

[47] Mruczkiewicz M, Krawczyk M, Gubbiotti G, et al. Nonreciprocity of spin waves in metallized magnonic crystal[J]. New Journal of Physics, 2013, 15(11): 113023.

[48] Beginin E N, Filimonov Yu A, Pavlov E S, et al. Bragg resonances of magnetostatic surface spin waves in a layered structure: Magnonic crystal-dielectric-metal[J]. Applied Physics Letters, 2012, 100(25): 252412.

[49] Alvarado-Seguel P, Gallardo R A. Band structure of a one-dimensional bilayer magnonic crystal[J]. Physical Review B, 2019, 100(14): 144415.

[50] Chumak A V, Tiberkevich V S, Karenowska A D, et al. All-linear time reversal by a dynamic artificial crystal[J]. Nature Communications, 2010, 1(1): 141.

[51] Topp J, Heitmann D, Kostylev M P, et al. Making a reconfigurable artificial crystal by ordering bistable magnetic nanowires[J]. Physical Review Letters, 2010, 104(20): 207205.

[52] Chumak A V, Neumann T, Serga A A, et al. A current-controlled, dynamic magnonic crystal[J]. Journal of Physics D: Applied Physics, 2009, 42(20): 205005.

[53] Wang Q, Chumak A V, Jin L, et al. Voltage-controlled nanoscale reconfigurable magnonic crystal[J]. Physical Review B, 2017, 95(13): 134433.

[54] Wang X guang, Guo G hua, Li Z xiong, et al. Spin-wave propagation in domain wall magnonic crystal[J]. EPL (Europhysics Letters), 2015, 109(3): 37008.

[55] Li Z xiong, Wang X guang, Wang D wei, et al. Reconfigurable magnonic crystal consisting of periodically distributed domain walls in a nanostrip[J]. Journal of Magnetism and Magnetic Materials, 2015, 388: 10-15.

[56] Ma F, Zhou Y, Braun H B, et al. Skyrmion-based dynamic magnonic crystal[J]. Nano Letters, 2015, 15(6): 4029-4036.

[57] Mruczkiewicz M, Gruszecki P, Zelent M, et al. Collective dynamical skyrmion excitations in a magnonic crystal[J]. Physical Review B, 2016, 93(17): 174429.

[58] Szulc K, Tacchi S, Hierro-Rodríguez A, et al. Reconfigurable magnonic crystals based on imprinted magnetization textures in hard and soft dipolar-coupled bilayers[J]. ACS Nano, 2022, 16(9): 14168-14177.

[59] Medlej I, Wang J, Hu C, et al. Hopfion based magnonic crystal[J]. Journal of Magnetism and Magnetic Materials, 2024, 591: 171726.

[60] Fert A, Reyren N, Cros V. Magnetic skyrmions: Advances in physics and potential applications[J]. Nature Reviews Materials, 2017, 2(7): 17031.

[61] Jiang W, Chen G, Liu K, et al. Skyrmions in magnetic multilayers[J]. Physics Reports, 2017, 704: 1-49.

[62] Göbel B, Mertig I, Tretiakov O A. Beyond skyrmions: Review and perspectives of alternative magnetic quasiparticles[J]. Physics Reports, 2021, 895: 1-28.

[63] Nagaosa N, Tokura Y. Topological properties and dynamics of magnetic skyrmions[J]. Nature Nanotechnology, 2013, 8(12): 899-911.

[64] Mühlbauer S, Binz B, Jonietz F, et al. Skyrmion lattice in a chiral magnet[J]. Science, 2009, 323(5916): 915-919.

[65] Zhang X, Zhou Y, Ezawa M. Magnetic bilayer-skyrmions without skyrmion Hall effect[J]. Nature Communications, 2016, 7(1): 10293.

[66] Iwasaki J, Mochizuki M, Nagaosa N. Current-induced skyrmion dynamics in constricted geometries[J]. Nature Nanotechnology, 2013, 8(10): 742-747.

[67] Pereiro M, Yudin D, Chico J, et al. Topological excitations in a kagome magnet[J]. Nature Communications, 2014, 5(1): 4815.

[68] Xing X, Pong P W T, Zhou Y. Current-controlled unidirectional edge-meron motion[J]. Journal of Applied Physics, 2016, 120(20): 203903.

[69] Chen J P, Lin J Q, Song X, et al. Control of Néel-type magnetic kinks confined in a square nanostructure by spin-polarized currents[J]. Frontiers in Physics, 2021, 9: 680698.

[70] Zhou Y, Ezawa M. A reversible conversion between a skyrmion and a domain-wall pair in a junction geometry[J]. Nature Communications, 2014, 5(1): 4652.

[71] Jiang W, Upadhyaya P, Zhang W, et al. Blowing magnetic skyrmion bubbles[J]. Science, 2015, 349(6245): 283-286.

[72] Fert A, Cros V, Sampaio J. Skyrmions on the track[J]. Nature Nanotechnology, 2013, 8(3): 152-156.

[73] Wang Z, Yuan H Y, Cao Y, et al. Magnonic frequency comb through nonlinear magnon-skyrmion scattering[J]. Physical Review Letters, 2021, 127(3): 037202.

[74] Zhang X, Ezawa M, Xiao D, et al. All-magnetic control of skyrmions in nanowires by a spin wave[J]. Nanotechnology, 2015, 26(22): 225701.

[75] Ding J, Yang X, Zhu T. The motion of magnetic skyrmions driven by propagating spin waves[J]. IEEE Transactions on Magnetics, 2015, 51(11): 1-4.

[76] Zhang X, Müller J, Xia J, et al. Motion of skyrmions in nanowires driven by magnonic momentum-transfer forces[J]. New Journal of Physics, 2017, 19(6): 065001.

[77] Shen M, Zhang Y, Ou-Yang J, et al. Motion of a skyrmionium driven by spin wave[J]. Applied Physics Letters, 2018, 112(6): 062403.

[78] Li S, Xia J, Zhang X, et al. Dynamics of a magnetic skyrmionium driven by spin waves[J]. Applied Physics Letters, 2018, 112(14): 142404.

[79] Song L, Yang H, Liu B, et al. A spin-wave driven skyrmion diode under transverse magnetic fields[J]. Journal of Magnetism and Magnetic Materials, 2021, 532: 167975.

[80] Bai X, Wang J, Yang J, et al. Dynamics of skyrmion bags driven by spin wave[J]. Journal of Magnetism and Magnetic Materials, 2023, 586: 171231.

[81] Ma X P, Ai X, Yang X X, et al. Gyromotion of skyrmion along the nanofilm edge driven by spin waves[J]. Journal of Magnetism and Magnetic Materials, 2023, 581: 170665.

[82] Moon K W, Chun B S, Kim W, et al. Control of spin-wave refraction using arrays of skyrmions[J]. Physical Review Applied, 2016, 6(6): 064027.

[83] Chen T, Dumas R K, Eklund A, et al. Spin-torque and spin-hall nano-oscillators[J]. Proceedings of the IEEE, 2016, 104(10): 1919-1945.

[84] Kiselev S I, Sankey J C, Krivorotov I N, et al. Microwave oscillations of a nanomagnet driven by a spin-polarized current[J]. Nature, 2003, 425(6956): 380-383.

[85] Sharma A, Tulapurkar A A, Muralidharan B. Resonant spin-transfer-torque nano-oscillators[J]. Physical Review Applied, 2017, 8(6): 064014.

[86] Arun R, Gopal R, Chandrasekar V K, et al. High-frequency oscillations in a spin-torque nano-oscillator due to bilinear coupling[J]. Physical Review B, 2023, 107(22): 224434.

[87] Pribiag V S, Krivorotov I N, Fuchs G D, et al. Magnetic vortex oscillator driven by d.c. spin-polarized current[J]. Nature Physics, 2007, 3(7): 498-503.

[88] Dussaux A, Georges B, Grollier J, et al. Large microwave generation from current-driven magnetic vortex oscillators in magnetic tunnel junctions[J]. Nature Communications, 2010, 1(1): 8.

[89] Grimaldi E, Dussaux A, Bortolotti P, et al. Response to noise of a vortex based spin transfer nano-oscillator[J]. Physical Review B, 2014, 89(10): 104404.

[90] Zhang S, Wang J, Zheng Q, et al. Current-induced magnetic skyrmions oscillator[J]. New Journal of Physics, 2015, 17(2): 023061.

[91] Jin C, Wang J, Wang W, et al. Array of synchronized nano-oscillators based on repulsion between domain wall and skyrmion[J]. Physical Review Applied, 2018, 9(4): 044007.

[92] Zhou S, Zheng C, Chen X, et al. Skyrmion-based spin-torque nano-oscillator in synthetic antiferromagnetic nanodisks[J]. Journal of Applied Physics, 2020, 128(3): 033907.

[93] Garcia-Sanchez F, Sampaio J, Reyren N, et al. A skyrmion-based spin-torque nano-oscillator[J]. New Journal of Physics, 2016, 18(7): 075011.

[94] Shen L, Xia J, Zhao G, et al. Spin torque nano-oscillators based on antiferromagnetic skyrmions[J]. Applied Physics Letters, 2019, 114(4): 042402.

[95] Feng Y, Zhu H, Zhang X, et al. Ultrahigh frequency spin-torque nano-oscillator based on bilayer-skyrmions[J]. Journal of Magnetism and Magnetic Materials, 2022, 543: 168641.

[96] Guo J H, Xia J, Zhang X C, et al. A ferromagnetic skyrmion-based nano-oscillator with modified profile of Dzyaloshinskii-Moriya interaction[J]. Journal of Magnetism and Magnetic Materials, 2020, 496: 165912.

[97] Jin C, Ma Y, Song C, et al. High-frequency spin transfer nano-oscillator based on the motion of skyrmions in an annular groove[J]. New Journal of Physics, 2020, 22(3): 033001.

[98] Feng Y, Xia J, Qiu L, et al. A skyrmion-based spin-torque nano-oscillator with enhanced edge[J]. Journal of Magnetism and Magnetic Materials, 2019, 491: 165610.

[99] Das D, Muralidharan B, Tulapurkar A. Skyrmion based spin-torque nano-oscillator[J]. Journal of Magnetism and Magnetic Materials, 2019, 491: 165608.

[100] Ma Y, Wang J, Zeng Z, et al. Multifunction spin transfer nano-oscillator based on elliptical skyrmion[J]. Journal of Magnetism and Magnetic Materials, 2022, 564: 170061.

[101] Donahue M. OOMMF User's Guide, Version 1.0[Z]. - 6376, National Institute of Standards and Technology, Gaithersburg, MD, 1999.

[102] Kotus K A, Moalic M, Zelent M, et al. Scattering of spin waves in a multimode waveguide under the influence of confined magnetic skyrmion[J]. APL Materials, 2022, 10(9): 091101.

[103] Vansteenkiste A, Leliaert J, Dvornik M, et al. The design and verification of MuMax3[J]. AIP Advances, 2014, 4(10): 107133.

[104] Beg M, Lang M, Fangohr H. Ubermag: Toward more effective micromagnetic workflows[J]. IEEE Transactions on Magnetics, 2022, 58(2): 1-5.

[105] Crépieux A, Lacroix C. Dzyaloshinsky--Moriya interactions induced by symmetry breaking at a surface[J]. Journal of Magnetism and Magnetic Materials, 1998, 182(3): 341-349.

[106] Hrabec A, Porter N A, Wells A, et al. Measuring and tailoring the Dzyaloshinskii-Moriya interaction in perpendicularly magnetized thin films[J]. Physical Review B, 2014, 90(2): 020402.

[107] Yu G, Upadhyaya P, Fan Y, et al. Switching of perpendicular magnetization by spin--orbit torques in the absence of external magnetic fields[J]. Nature Nanotechnology, 2014, 9(7): 548-554.

[108] Woo S, Litzius K, Krüger B, et al. Observation of room-temperature magnetic skyrmions and their current-driven dynamics in ultrathin metallic ferromagnets[J]. Nature Materials, 2016, 15(5): 501-506.

[109] Jiang W, Zhang X, Yu G, et al. Direct observation of the skyrmion Hall effect[J]. Nature Physics, 2017, 13(2): 162-169.

[110] Landau L D, Lifshitz E M. On the theory of the dispersion of magnetic permeability in ferromagnetic bodies[C]. 1935.

[111] Gilbert T L. Classics in magnetics a phenomenological theory of damping in ferromagnetic materials[J]. IEEE Transactions on Magnetics, 2004, 40(6): 3443-3449.

[112] Rohart S, Thiaville A. Skyrmion confinement in ultrathin film nanostructures in the presence of Dzyaloshinskii-Moriya interaction[J]. Physical Review B, 2013, 88(18): 184422.

[113] Yang S H, Ryu K S, Parkin S. Domain-wall velocities of up to 750 ms−1 driven by exchange-coupling torque in synthetic antiferromagnets[J]. Nature Nanotechnology, 2015, 10(3): 221-226.

[114] Tomasello R, Puliafito V, Martinez E, et al. Performance of synthetic antiferromagnetic racetrack memory: domain wall versus skyrmion[J]. Journal of Physics D: Applied Physics, 2017, 50(32): 325302.

[115] Liu C, Chen J, Liu T, et al. Long-distance propagation of short-wavelength spin waves[J]. Nature Communications, 2018, 9(1): 738.

[116] 自旋波分析程序：MFA改进版[EB]//https://download.csdn.net/download/qq_43572058/87346736.

[117] Wang Q, Heinz B, Verba R, et al. Spin pinning and spin-wave dispersion in nanoscopic ferromagnetic waveguides[J]. Physical Review Letters, 2019, 122(24): 247202.

[118] Le Maho Y, Kim J V, Tatara G. Spin-wave contributions to current-induced domain wall dynamics[J]. Physical Review B, 2009, 79(17): 174404.

[119] Demidov V E, Kostylev M P, Rott K, et al. Excitation of microwaveguide modes by a stripe antenna[J]. Applied Physics Letters, 2009, 95(11): 112509.

[120] Gallardo R A, Cortés-Ortuño D, Schneider T, et al. Flat bands, indirect gaps, and unconventional spin-wave behavior induced by a periodic Dzyaloshinskii-Moriya interaction[J]. Physical Review Letters, 2019, 122(6): 067204.

[121] Xing X, Li S, Huang X, et al. Engineering spin-wave channels in submicrometer magnonic waveguides[J]. AIP Advances, 2013, 3(3): 032144.

[122] Romming N, Hanneken C, Menzel M, et al. Writing and deleting single magnetic skyrmions[J]. Science, 2013, 341(6146): 636-639.

[123] Zhang W, Jiang B, Wang L, et al. Enhancement of interfacial Dzyaloshinskii-Moriya interaction: A comprehensive investigation of magnetic dynamics[J]. Physical Review Applied, 2019, 12(6): 064031.

[124] Xing X, Åkerman J, Zhou Y. Enhanced skyrmion motion via strip domain wall[J]. Physical Review B, 2020, 101(21): 214432.

[125] Yang S, Wu K, Zhao Y, et al. Inhibition of skyrmion hall effect by a stripe domain wall[J]. Physical Review Applied, 2022, 18(2): 024030.

[126] Xing X, Zhou Y. Skyrmion motion and partitioning of domain wall velocity driven by repulsive interactions[J]. Communications Physics, 2022, 5(1): 241.

[127] Deng P, Zhuo F, Li H, et al. Mirroring skyrmions in synthetic antiferromagnets via modular design[J]. Nanomaterials, 2023, 13(5): 859.

[128] Karayev S, Murray P D, Khadka D, et al. Interlayer exchange coupling in Pt/Co/Ru and Pt/Co/Ir superlattices[J]. Physical Review Materials, 2019, 3(4): 041401.

[129] Yang H, Wang C, Wang X, et al. Twisted skyrmions at domain boundaries and the method of image skyrmions[J]. Physical Review B, 2018, 98(1): 014433.

[130] 从OVF矢量场文件中获取磁斯格明子的位置和半径的粗略方法（trace skyrmion）[EB]//https://blog.csdn.net/qq_43572058/article/details/131617080.

[131] Patimisco P, Sampaolo A, Bidaux Y, et al. Purely wavelength- and amplitude-modulated quartz-enhanced photoacoustic spectroscopy[J]. Optics Express, 2016, 24(23): 25943.

[132] Romming N, Kubetzka A, Hanneken C, et al. Field-dependent size and shape of single magnetic skyrmions[J]. Physical Review Letters, 2015, 114(17): 177203.

[133] Wang X S, Yuan H Y, Wang X R. A theory on skyrmion size[J]. Communications Physics, 2018, 1(1): 31.

攻读学位期间取得与学位论文相关的成果

发表和投稿与学位论文相关的学术论文

Qiyun Yi, Zhenhua Tang, Daoyun Zhu, Xiangjun Xing, Wei Zhang, and Yan Zhou. Magnonic bandgap openings and in-gap propagating states in domain-wall waveguides induced by periodic modulations. Physical Review B. 109, 184401 (2024). (SCI Impact Factor 3.7)
Qiyun Yi, Ting Han, Jinyi Jiang, and Xiangjun Xing. A spin-torque nano-oscillator based on interlayer-coupled meron-skyrmion pairs with a fixed orbit. Journal of Applied Physics. 135, 183901 (2024). (SCI Impact Factor 3.2)