一,IIR滤波器
在FPGA - 滤波器 - FIR滤波器设计中可知,数字滤波器是一个时域离散系统。任何一个时域离散系统都可以用一个N阶差分方程来表示,即:
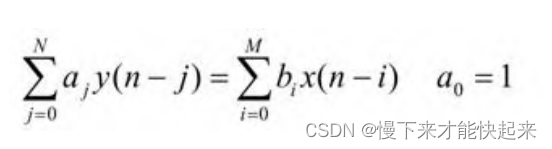
式中,x(n)和y(n)分别是系统的输入序列 和输出序列 ;aj和bi均为常数;y(n-j)和x(n-i)项只有一次幂,没有相互交叉相乘项,故称为线性常系数差分方程 。差分方程的阶数是由方程y(n-j)项中j的最大值与 最小值之差确定的。式中,y(n-j)项j的最大值取N,最小值取 0,因此称为N阶差分方程。
当aj=0且j>0时,N阶差分方程表示的系统为FIR滤波器 。当aj≠0 且 j>0 时 ,N阶差分方程表 示的系统为IIR( Infinite Impulse Response)滤波器。
IIR滤波器的单位脉冲响应是无限长的,其系统函数为:

系统的差分方程可以写成:
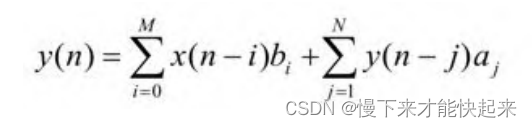
从系统的差分方程可以很容易看出,IIR滤波器有以下几个显著特性。
- IIR滤波器同时存在不为零的极点和零点,要保证IIR滤波器是稳定的系统,需要使系统的极点在单位圆内。也就是说,系统的稳定性是由系统的极点决定的。
- 由于线性相位滤波器 所有的零点和极点 都是关于单位圆对称 的,所以只允许极点位于单位圆的原点 。由于IIR滤波器存在不为零的极点 ,因此只可能实现近似的线性相位特性。也正是因为IIR滤波器的非线性相位特性限制了其应用范围。
- 在FPGA 等数字硬件平台上实现IIR滤波器 时,由于存在反馈结构,因此受限于寄存器的长度,无法通过增加字长来实现全精度的运算,运算过程中的**有限字长效应**是实现IIR滤波器时必须考虑的问题。
二,FIR滤波器和IIR滤波器比较
IIR滤波器与FIR滤波器是最常见的数字滤波器,两者的结构及分析方法相似。为了更好地理解这两种数字滤波器的异同,下面对它们进行简单的比较:
- 在满足相同幅频响应设计指标的情况下,FIR滤波器的阶数 通常是IIR滤波器的阶数的5~10倍。
- FIR滤波器能得到严格的线性相位特性 (当FIR滤波器系数具 有对称结构时)。在相同的阶数情况下,IIR滤波器具有更好的幅度特性 ,但相位特性是非线性的。
- FIR滤波器的单位脉冲响应是有限长的,一般采用非递归结构 ,必定是稳定的系统 ,即使在有限精度运算时,误差也比较小,受有限字长效应的影响较小。IIR滤波器必须采用递归结构 ,只有极点在单位圆内时才是稳定的系统;IIR滤波器具有反馈结构,由于运算过程中的截位处理,容易引起振荡现象。
- FIR滤波器 的运算是一种卷积运算 ,可以采用快速傅里叶变换 和其他快速算法 ,运算速度快。IIR滤波器无法采用类似的快速算法。
- 在设计方法上,IIR滤波器 可以利用模拟滤波器的设计公式、数据和表格等资料 。FIR滤波器不能借助模拟滤波器 的设计成果。 由于计算机设计软件的发展,在设计FIR滤波器和IIR滤波器时均可采用现成的函数,因此在工程设计中两者的设计难度均已大幅下降。
- IIR滤波器主要用于设计规格化的、频率特性为分段恒定的标准滤波器 ,FIR滤波器要灵活得多,适应性更强。
- 在FPGA设计中,FIR滤波器可以采用现成的IP核进行设计 , 工作量较小 ;用于IIR滤波器设计的IP核很少,一般需要手动编写代码 ,工作量较大。
- 当给定幅频响应 ,而不考虑相位特性 时,如果FPGA的逻辑资源较少,则可采用IIR滤波器 ;当要求滤波器具有严格线性相位特性 , 或幅度特性不同于典型模拟滤波器的特性时,通常采用FIR滤波器
三,IIR滤波器的MATLAB设计
一般来讲,IIR滤波器的设计方法可以分为三种:原型转换法 、直接设计法 ,以及直接调用MATLAB中设计IIR滤波器的函数 。从工程设计 的角度来讲,前两种设计方法都比较烦琐,且需要对IIR滤波器的基础 理论知识有更多的了解,因此工程中大多直接调用MATLAB中设计IIR滤波器的函数。
MATLAB提供了多种用于设计IIR滤波器的函数,通常采用的是根据 原型转换法实现的5种设计 IIR滤波器的函数:butter()函数(巴特沃斯函数) 、cheby1()函数(切比雪夫I型函数) 、cheby2()函数(切比雪夫Ⅱ型函数) 、ellip()函数(椭圆滤波器函数) 及yulewalk()函数。
3.1 butter()函数设计IIR滤波器
在MATLAB中,可以利用butter()函数直接设计各种形式的数字滤 波器(也可设计模拟滤波器),其语法为:
[b,a] = butter(n,Wn);
[b,a] = butter(n,Wn,'ftype');
[z,p,k] = butter(n,Wn);
[z,p,k] = butter(n,Wn,'ftype');
[A,B,C,D] = butter(n,Wn);
[A,B,C,D] = butter(n,Wn,'ftype');butter()函数 可以设计低通 、高通 、带通 和带阻等各种形式的滤波器。
输入参数 :
n - 滤波器阶数 整数标量
Wn - 截止频率,注意:Wn = fc_low/(fs/2) 标量 | 二元素向量
ftype - 滤波器类型 'low' | 'bandpass' | 'high' | 'stop'
输出参数:
b,a - 传递函数系数 行向量
z,p,k - 零点、极点和增益 列向量、标量
A,B,C,D - 状态空间矩阵 矩阵
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz 的高通巴特沃斯数字滤波器,并画出滤波器的频率响应,只需在 MATLAB中使用下面的命令即可。
[b,a] = butter(12,600*2/2000,'high');
freqz(b,a,128,2000);3.2 cheby1()函数设计IIR滤波器
在MATLAB中,可以利用cheby1()函数直接设计各种形式的数字滤 波器(也可设计模拟滤波器),其语法为:
[b,a] = cheby1(n,Rp,Wn);
[b,a] = cheby1(n,Rp,Wn,'ftype');
[z,p,k] = cheby1(n,Rp,Wn);
[z,p,k] = cheby1(n,Rp,Wn,'ftype');
[A,B,C,D] = cheby1(n,Rp,Wn);
[A,B,C,D] = cheby1(n,Rp,Wn,'ftype');cheby1函数先设计出切比雪夫I型的模拟原型滤波器 ,然后用原型变换法 得到数字低通、高通、带通或带阻滤波器。切比雪夫I型滤波器 在通带是等纹波的,在阻带是单调的,可以设计低通、高通、带通和 带阻各种形式的滤波器。
输入参数 :
n - 滤波器阶数 整数标量
Rp -通带纹波最大衰减 单位(dB)
Wn - 截止频率,注意:Wn = fc_low/(fs/2) 标量 | 二元素向量
ftype - 滤波器类型 'low' | 'bandpass' | 'high' | 'stop'
输出参数:
b,a - 传递函数系数 行向量
z,p,k - 零点、极点和增益 列向量、标量
A,B,C,D - 状态空间矩阵 矩阵
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz、通带衰减为0.5 dB的低通切比雪夫I型数字滤波器,并画出滤波器的频率响应,只需在MATLAB中使用以下命令即可。
[b,a] = cheby1(12,0.5,600*2/2000);
freqz(b,a,128,2000);3.3 cheby2()函数设计IIR滤波器
用cheby2()函数直接设计各种形式的数字滤波器(也可设计模拟滤波器)。
函数的使用方法与cheby1()完全相同,只是利用cheby1()函数设计的滤波器在通带是等纹波的 ,在阻带是单调 的;而利用cheby2()函数设计的滤波器在阻带是等纹波的,在通带是单调的。
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz、通带衰减为0.5 dB的低通切比雪夫II型数字滤波器,并画出滤波器的频率响应,只需在MATLAB中使用以下命令即可。
[b,a] = cheby2(12,0.5,600*2/2000);
freqz(b,a,128,2000);3.4 ellip()函数设计IIR滤波器
在MATLAB中,可以利用ellip()函数直接设计各种形式的数字滤波 器(也可设计模拟滤波器),其语法为:
[b,a] = ellip(n,Rp,Rs,Wn);
[b,a] = ellip(n,Rp,Rs,Wn,'ftype');
[z,p,k] = ellip(n,Rp,Rs,Wn);
[z,p,k] = ellip(n,Rp,Rs,Wn,'ftype');
[A,B,C,D] = ellip(n,Rp,Rs,Wn);
[A,B,C,D] = ellip(n,Rp,Rs,Wn,'ftype');在利用ellip()函数设计IIR滤波器 时,先设计出椭圆滤波器 ,然后用原型变换法 得到数字低通 、高通、带通或带阻 滤波器。在模拟滤波器的设计中,采用椭圆滤波器 的设计是最为复杂的一种设计方法, 但它设计出的滤波器的阶数最小 ,同时它对参数的量化灵敏度最敏感。
输入参数 :
n - 滤波器阶数 整数标量
Rp -通带纹波最大衰减 单位(dB)
Rs -阻带波纹最小衰减 单位 (dB)
Wn - 截止频率,注意:Wn = fc_low/(fs/2) 标量 | 二元素向量
ftype - 滤波器类型 'low' | 'bandpass' | 'high' | 'stop'
输出参数:
b,a - 传递函数系数 行向量
z,p,k - 零点、极点和增益 列向量、标量
A,B,C,D - 状态空间矩阵 矩阵
例如,要设计采样频率为2000 Hz、阶数为12、截止频率为600 Hz、通带衰减为5dB、阻带衰减为80 dB的低通椭圆滤波器 ,并画出滤波器的频率响应,只需在MATLAB中使用以下命令即可。
[b,a] = ellip(12,5,8,0,600*2/2000);
freqz(b,a,128,2000);3.5 yulewalk()函数设计IIR滤波器
在MATLAB中,yulewalk()函数用于设计递归数字滤波器 。与前面介绍的几种IIR滤波器设计函数不同 的是,yulewalk()函数只能设计数字滤波器,不能设计模拟滤波器 。yulewalk()实际是一种在频域采用 了最小均方法来设计滤波器的函数,其语法形式为:
[b,a] = yulewalk(n,f,m)yulewalk()函数中的参数n 表示滤波器的阶数,f 和m 用于表征滤波器的幅频响应。其中f是一个向量 ,它的每一个元素都是0~1的实数 ,表示频率 ,其中1表示采样频率的1/2 ,且f中的元素必须是递增的,第 一个元素必须是0,最后一个元素必须是1 。m是频率f处的幅度响应 , 它也是一个向量,长度与f相同。当确定了理想滤波器的频率响应后, 为了避免从通带到阻带的过渡陡峭,应对过渡带宽进行多次仿真试验,以便得到最优的滤波器设计。
例如,要设计一个12阶的低通滤波器,滤波器的截止频率为600 Hz,采样频率为2000 Hz,采用yulewalk()函数的设计方法为:
f = [0 600*2/2000 600*2/2000 1];
m = [1 1 0 0];
[b,a] = yulewalk(9,f,m);
freqz(b,a,128,2000);3.6 使用FDATOOL设计IIR滤波器
除了一些常用的滤波器函数,MATLAB还提供了数字滤波器 的专用 设计工具FDATOOL。FDATOOL的突出优点是直观、方便,用户只需设置几个参数,即可查看IIR滤波器频率响应、零点/极点、单位脉冲响应、系数等信息。
例子:采用FDATOOL设计带通IIR滤波器
采用FDATOOL设计一个带通IIR滤波器,通带范围为1200~2400 Hz ,低频过渡带宽为900~1200 Hz ,高频过渡带宽为2400~2700 Hz , 采样频率为9000 Hz 的等阻带纹波滤波器 ,要求阻带衰减大于70 dB。
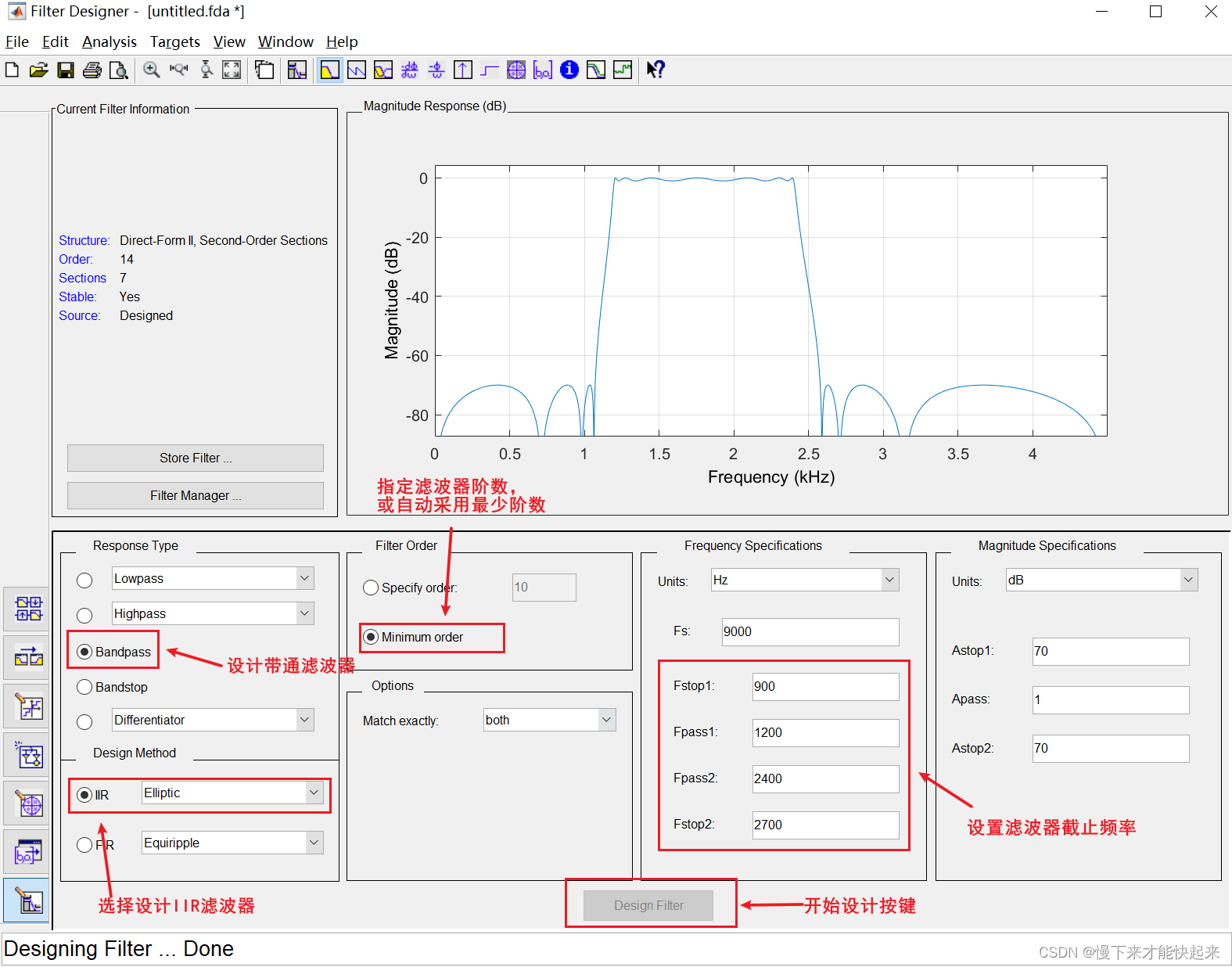
启动MATLAB后,在命令行窗口中输入"fdatool"后按下回车键, 即可打开FDATOOL界面,如上图所示。
- 第一步:在**"Frequency Specifications"**中设置IIR滤波器的 截止频率。
- 第二步:在**"Response Type"** 中选中**"Bandpass"** ,表示设计的是带通IIR滤波器。
- 第三步:在"Design Method "中选中"IIR",在"IIR"的下 拉列表中选择"Elliptic"。
- 第四步:在**"Filter Order"** 中选中**"Minimum order"** ,表示 采用最小阶数来完成设计。
- 第 五 步 : 单 击 FDATOOL 界 面 左 下 方 的 " " 按 钮 ( Design Filter,滤波器设计)即可开始IIR滤波器的设计。
- 第六步:根据FDATOOL中的幅频响应曲线调整IIR滤波器的阶数, 直到满足设计要求为止。
- 至此,使用FDATOOL完成了带通滤波器的设计,用户可以通过 单击菜单"Analysis→ Filter Coefficients"来查看IIR滤波器的系数。
四,IIR滤波器的FPGA实现
4.1 IIR滤波器系数的量化方法
例如,采用cheby2()函数 设计一个阶数为7(长度为8) 、采样频率为12.5MHz 、截 止频率为3.125MHz 、阻带衰减为60 dB 的低通IIR滤波器,可在MATLAB 的命令行窗口中直接输入下面的命令:
[b,a] = cheby2(7,60,0.5);按回车键后,可以直接在命令行窗口中获取低通IIR滤波器的系数 向量,即:

在进行FPGA实现 时,必须对低通IIR滤波器的系数进行量化处理 ,**如对系数进行12 bit量化,**可在MATLAB命令行窗口中直接输入下面的 命令:
m = max(max(abs(a),abs(b)));
Qb = round(b/m*(2^(12-1)-1));
Qa = round(a/m*(2^(12-1)-1));即:

Qb = [13 38 74 99 99 74 38 13]
Qa = [900 -1632 2047 -1427 725 -215 42 -3]根据低通IIR滤波器系统函数,可直接写出其差分方程,即:
900y(n)=13[x(n)+x(n-7)]+38[x(n-1)+x(n-6)]+74[x(n-2)+x(n-5)]+99[x(n-3)+x(n-4)]
-[-1623y(n-1)+2047y(n-2)-1427y(n-3)+725y(n-4)-215y(n-5)+42y(n-6)-3y(n-7)]需要特别注意的是,上式的左边乘了一个常系数,即量化后 的Qa(1)。由于上式的递归特性,为了正确求解下一个输出值, 需要在计算上式右边后除以900,以获取正确的输出结果。也就是说,在FPGA实现时需要增加一级常数除法运算。
在进行除法运算的FPGA实现 时,即使常系数的除法运算,也是十分耗费资源 的。但当除数是2的整数幂次方时,可根据二进制数运算的特点,直接采用移位的方法 来近似实现除法运算 。移位运算不仅占用 的硬件资源少,而且运算速度快 。因此,在上式所表示的低通IIR滤波器时,一个简单可行的方法是在进行系数量化时,有意将量化后的分母项系数的第一项设置为2的整数幂次方。仍然采用MATLAB来 对低通IIR滤波器系数进行量化,其命令为:
m = max(max(abs(a),abs(b)));
Qm = floor(log2(m/a(1)));
if Qm < log2(m/a(1))
Qm = Qm + 1;
end
Qm = 2^Qm;
Qb = round(b/Qm*(2^(12-1)-1));
Qa = round(a/Qm*(2^(12-1)-1));
disp(Qb);
disp(Qa);即:

Qb = [ 7 21 42 56 56 42 21 7]
Qa = [512 -922 1163 -811 412 -122 24 -2]4.2 IIR滤波器的FPGA设计
对上述例子所述的IIR滤波器进行Verilog HDL设计,并仿真测试 FPGA实现后的IIR滤波效果,其中系统时钟信号频率为12.5 MHz 、数据输入速率为12.5 MHz 、输入数据的位宽为8,对IIR滤波器的系数进行12 bit量化。
所要实现的IIR滤波器的差分方程为:
512y(n)=7[x(n)+x(n-7)]+21[x(n-1)+x(n-6)]+42[x(n-2)+x(n-5)]+56[x(n-3)+x(n-4)]
-[-922y(n-1)+1163y(n-2)-811y(n-3)+412y(n-4)-122y(n-5)+24y(n-6)-2y(n-7)] 计算上式右边后,再除以512即可完成一次完整的滤波运 算。根据FPGA的特点 ,可采用右移9 bit的方法来近似实现除以512运算 。因此,直接型结构IIR滤波器的实现结构如图表示。

从上图可以看出,对于零点处(零点系数)直接型结构IIR滤波器 实现结构,其实可完全看成没有反馈结构的FIR滤波器 ,并且可以利用对称系数的特点 进一步减少乘法运算 。对于极点处(极点系数)直接型结构IIR滤波器 的实现结构,即求取Yout信号的过程,也可以看成 一个没有反馈结构的FIR滤波器 。整个IIR滤波器的闭环过程是在求取Ysum 的减法器 ,以及移位算法 实现除法运算的过程中完成的。
4.2.1 零点系数的Verilog 代码设计
零点处的IIR滤波器可完全看成FIR滤波器,因此可采用FIR滤波器 的FPGA实现方法。
代码如下:
module zero_point(
input clk ,
input reset ,
input signed [7 :0] Xin ,
output signed [15:0] Xout
);
reg signed [7:0]Xin_reg [7:0];
reg [3:0] i;
reg [3:0] j;
//数据存入到移位寄存器
always @(posedge clk or negedge reset) begin
if(reset) begin
for(i=0;i<8;i=i+1)
Xin_reg[i] <= 8'd0;
end else begin
for(j=0;j<8;j=j+1)
Xin_reg[j+1] <= Xin_reg[j];
Xin_reg[0] <= Xin;
end
end
//对称系数的输入数据相加
wire signed [8:0] Add_reg[3:0];
assign Add_reg[0] = Xin_reg[0] + Xin_reg[7];
assign Add_reg[1] = Xin_reg[1] + Xin_reg[6];
assign Add_reg[2] = Xin_reg[2] + Xin_reg[5];
assign Add_reg[3] = Xin_reg[3] + Xin_reg[4];
//采用移位(左移)相加方法实现乘法运算
wire [15:0] Mult_reg[3:0];
assign Mult_reg[0] = {{6{Add_reg[0][8]}},Add_reg[0],2'd0}
+ {{7{Add_reg[0][8]}},Add_reg[0],1'd0}
+ {{8{Add_reg[0][8]}},Add_reg[0]}; //7 = 2^2 + 2^1 + 2^0
assign Mult_reg[1] = {{4{Add_reg[1][8]}},Add_reg[1],4'd0}
+ {{6{Add_reg[1][8]}},Add_reg[1],2'd0}
+ {{8{Add_reg[1][8]}},Add_reg[1]}; //12 = 2^4 + 2^2 + 2^0
assign Mult_reg[2] = {{3{Add_reg[2][8]}},Add_reg[2],5'd0}
+ {{5{Add_reg[2][8]}},Add_reg[2],3'd0}
+ {{7{Add_reg[2][8]}},Add_reg[2],1'd0}; //42 = 2^5 + 2^3 + 2^1
assign Mult_reg[3] = {{3{Add_reg[3][8]}},Add_reg[3],5'd0}
+ {{4{Add_reg[3][8]}},Add_reg[3],4'd0}
+ {{5{Add_reg[3][8]}},Add_reg[3],3'd0}; //56 = 2^5 + 2^4 + 2^3
//对IIR滤波器系数与输入数据的相乘结果进行累加,
assign Xout = Mult_reg[0] + Mult_reg[1] + Mult_reg[2] + Mult_reg[3];
endmodule4.2.2 极点系数的Verilog 代码设计
极点处的IIR滤波器也可可完全看成一个FIR滤波器,因此可采用 FIR滤波器的FPGA实现方法。

其中:
Zero(n) = 7[x(n)+x(n-7)]+21[x(n-1)+x(n-6)]+42[x(n-2)+x(n-5)]+56[x(n-3)+x(n-4)]
Pole(n) = [-922y(n-1)+1163y(n-2)-811y(n-3)+412y(n-4)-122y(n-5)+24y(n-6)-2y(n-7)]
y(n) = [zero(n)-Pole(n)]/512 (8-14)由于极点系数绝对值的和为3456(922+1163+811+412+122+24+2)(不包括y(n)前面的系数512), 因此输出数据相对于输入数据需增加12 bit,共20 bit。
代码如下:
module pole_point (
input clk ,
input reset ,
input signed [7 :0] Yin ,
output signed [15:0] Yout
);
reg signed [7:0]Yin_reg[6:0];
reg [3:0] i;
reg [3:0] j;
//将数据存入到以为寄存器Yin_reg中
always @(posedge clk or negedge reset) begin
if(reset) begin
for(i=0;i<7;i=i+1)
Yin_reg[i] <= 8'd0;
end else begin
for(j=0;j<7;j=j+1)
Yin_reg[j+1] <= Yin_reg[j];
Yin_reg[0 ] <= Yin;
end
end
//实例化有符号乘法器IP核
wire signed [11:0] coe [7:0];
wire signed [19:0] Mult_reg[6:0];
// assign coe[0] = 12'd512;
assign coe[1] = 12'd922;
assign coe[2] = 12'd1163;
assign coe[3] = 12'd811;
assign coe[4] = 12'd412;
assign coe[5] = 12'd122;
assign coe[6] = 12'd24;
assign coe[7] = 12'd2;
mult u1(.a(coe[1]), .b(Yin_reg[0]), .p(Mult_reg[0]));
mult u2(.a(coe[2]), .b(Yin_reg[1]), .p(Mult_reg[1]));
mult u3(.a(coe[3]), .b(Yin_reg[2]), .p(Mult_reg[2]));
mult u4(.a(coe[4]), .b(Yin_reg[3]), .p(Mult_reg[3]));
mult u5(.a(coe[5]), .b(Yin_reg[4]), .p(Mult_reg[4]));
mult u6(.a(coe[6]), .b(Yin_reg[5]), .p(Mult_reg[5]));
mult u7(.a(coe[7]), .b(Yin_reg[6]), .p(Mult_reg[6]));
//对IIR滤波器系数和输入数据相乘结果累加
assign Yout = Mult_reg[0] + Mult_reg[1] + Mult_reg[2] + Mult_reg[3] +
Mult_reg[4] + Mult_reg[5] + Mult_reg[6];
endmodule4.2.3 顶层文件的代码设计
顶层文件代码:
module IIR_filter (
input clk ,
input reset ,
input signed [7 :0] din ,
output signed [15:0] dout
);
//例化 零点 极点模块
wire [15:0]Xout;
wire signed [7: 0]Yin;
wire signed [19:0]Yout;
wire signed [20:0]Ysum;
zero_point zero_point_inst(
.clk (clk) ,
.reset (reset) ,
.Xin (din) ,
.Xout (Xout)
);
pole_point pole_point_inst(
.clk (clk) ,
.reset (reset) ,
.Yin (Yin) ,
.Yout (Yout)
);
assign Ysum = Xout - Yout;
//IIR滤波器系数中的a(1) = 512,需要将加法结果除以512,可采用右移9位方法实现
wire signed [20:0] Ydiv;
assign Ydiv = {{9{Ysum[20]}},Ysum[20:9]};
//IIR滤波器输出数据范围与输入数据范围相同
assign Yin = (reset) ? 8'd0 : Ydiv[7:0];
assign dout = Yin;
endmoduleIIR滤波器 输出数据为Ysum除以512 的结果。为 了减少运算资源、提高运算速度,可采用右移9位的方法来实现近似除以512的运算。由于IIR滤波器的输出数据的位宽与输入数据的位宽相 同,因此直接取Ydiv的低8bit作为IIR滤波器的最终输出数据。
参考文献:
1\]刘谋,张梦豪,余丽仙,等.基于FPGA的IIR数字滤波器设计方法\[J\].电子技术,2020,49(11):1-3. \[2\]杜勇.Xilinx FPGA 数字信号处理设计\[M\].电子工业出版社:202003.339. \[3\]黄玉健,黄永庆.基于Matlab的级联型IIR滤波器设计与FPGA实现\[J\].梧州学院学报,2018,28(06):26-32. \[4\]陈鑫磊,辛晓宁,黄鑫.IIR数字滤波器设计与FPGA实现\[J\].微处理机,2018,39(01):43-47. \[5\]李秀花,马雯.基于FPGA的IIR数字滤波器设计与实现\[J\].电子技术,2016,45(05):58-60.