目录
整数对最小和
考察排序,数组拍平
题目描述
给定两个整数数组array1、array2,数组元素按升序排列。假设从array1、array2中分别取出一个元素可构成一对元素,
现在需要取出k对元素,并对取出的所有元素求和,计算和的最小值
注意
两对元素如果对应于array1、array2中的两个下标均相同,则视为同一对元素。
输入描述
输入两行数组array1、array2,每行首个数字为数组大小size(0 < size <= 100);
0 < array1[i] <= 1000
0 < array2[i] <= 1000
接下来一行为正整数k
0 < k <= array1.size() * array2.size()
输出描述
满足要求的最小和
示例1
输入
1 1 2 3
1 2 3 3
2
输出
4
说明
用例中,需要取2对元素
取第一个数组第0个元素与第二个数组第0个元素组成1对元素[1,1];
取第一个数组第1个元素与第二个数组第0个元素组成1对元素[1,1];
求和为1+1+1+1=4,为满足要求的最小和
解析
新建一个二维数组,数组的行列长度和array1、array2的长度对应,通过循环给数组的每一位赋值,
arr[i][j]表示的为一对元素的和,将二维数组拍平,然后按升序排列,取前k位的和即为满足要求的最小和。
答案
javascript
function calcPairSum(str){
let arr = str.split('\n')
let n = Number(arr.pop())
let [array1,array2]=arr.map(v=>v.split(' ').map(Number))
let len1 = array1.length;
let len2 = array2.length
arr = new Array(len1).fill(0).map(v=>new Array(len2).fill(0))
for(let i = 0;i<len1;i++){
for(let j = 0;j<len2;j++){
arr[i][j]=array1[i]+array2[j]
}
}
arr=arr.flat().sort((a,b)=>a-b)
return arr.slice(0,n).reduce((t,v,i)=>t+v)
}
console.log(calcPairSum(`1 1 2 3
1 2 3 3
2`))素数之积
考察数学素数定义
题目描述
RSA加密算法在网络安全世界中无处不在,它利用了极大整数因数分解的困难度,数据越大,安全系数越高,给定一个32位正整
数,请对其进行因数分解,找出是哪两个素数的乘积。
输入描述
一个正整数num
0<num <= 2147483647
输出描述
如果成功找到,以单个空格分割,从小到大输出两个素数,分解失败,请输出-1-1
示例1
输入
15
输出
35
说明
因数分解后,找到两个素数3和5,使得3*5=15,按从小到大排列后,输出3 5
示例2
输入
27
输出
-1-1
说明
通过因数分解,找不到任何索数,使得他们的乘积为27,输出-1-1
解析
javascript
function resolvePrimeNumber(n){
for(let i=2;i<=n**0.5;i++){
if(n%i===0){
let tmp = n/i
if(isPrime(tmp)&&isPrime(i)){
return [tmp,i].sort((a,b)=>a-b).join(' ')
}
}
}
return '-1 -1'
}
function isPrime(n){
for(let i=2;i<=n**0.5;i++){
if(n%i===0){
return false
}
}
return true
}
console.log(resolvePrimeNumber(15))
console.log(resolvePrimeNumber(27))找城市
考察深度遍历,递归,数组去重,字符串分割。
题目描述
一张地图上有n个城市,城市和城市之间有且只有一条道路相连:要么直接相连,要么通过其它城市中转相连(可中转一次或多次)。
城市与城市之间的道路都不会成环。 当切断通往某个城市 i 的所有道路后,地图上将分为多个连通的城市群,设该城市i的聚集度为DPi
(Degree of Polymerization), DPi = max(城市群1的城市个数, 城市群2的城市个数, ... 城市群m的城市个数)。
请找出地图上 DP 值最小的城市(即找到城市 j,使得 DPj = min(DP1, DP2 ... DPn) )
提示:如果有多个城市都满足条件,这些城市都要找出来(可能存在多个解)。
提示:DPi的计算,可以理解为已知一棵树,删除某个节点后,生成的多个子树,求解多个子树节点数的问题。
输入
每个样例:第一行有一个整数N,表示有N个节点。1<=N<=1000
接下来的N-1行每行有两个整数x,y,表示城市x与城市y连接。1<=x, y<=N
输出
输出城市的编号。如果有多个,按照编号升序输出。
示例1
输入
5
1 2
2 3
3 4
4 5
输出
3
示例2
输入
6
1 2
2 3
2 4
4 5
4 6
输出
2 4
说明
当切断通往城市3的所有道路后,1,2为一个城市群,4,5为一个城市群,DPi为2,此时DPi为其它Dpi中最小的,所以为城市3
解析
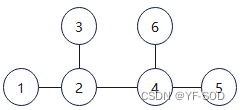
通过深度遍历,每次遍历一个元素就将该元素加入一个数组,遍历完后再将这个元素加入一遍,这样我们通过该元素分割时就可以拿到切断该元素后的相连的节点。
例如上图(示例2),我们通过上面遍历方法得出的数组为[1,2,3,2,4,5,4,6,4,2,1]。然后我们将这个数组形成一个环,这样对每个数进行切割后得到的数组内去重后就是一个城市群,例如对2进行切割,可以拿到[1],[3],[4,5,4,6,4],[1]然后由于是环,所以第一个和最后一个是一组,最后去重后就是分组结果[1][3][4,5,6],所以可以得到DPi为3即取[4,5,6]。
答案
javascript
function getDP(str) {
let arr = str.split('\n')
let n = arr.shift()
let obj = {}
arr.forEach(v => {
v = v.split(' ')
if (!obj[v[0]]) {
obj[v[0]] = { value: v[0], next: [] }
}
if (!obj[v[1]]) {
obj[v[1]] = { value: v[1], next: [] }
}
obj[v[0]].next.push(obj[v[1]])
obj[v[1]].next.push(obj[v[0]])
})
let start = Object.values(obj).filter(v => v.next.length === 1)[0]
let pathArr = dfs(start)
let pathStr = pathArr.join(' ')
let citys = uni(pathArr)
let dp = Infinity
let dpCitys = []
for (let i = 0; i < n; i++) {
let cur = citys[i]
let tmp = pathStr.split(cur).map(v => v.split(' '))
//第一个节点和最后一个节点合成一个
tmp[0] = tmp[0].concat(tmp.pop())
let dpi = 1
tmp.forEach(v => {
let tmpDpi = uni(v.filter(city => city !== '')).length
if (tmpDpi > dpi) {
dpi = tmpDpi
}
})
if (dpi < dp) {
dpCitys = [cur]
dp = dpi
} else if (dpi === dp) {
dpCitys.push(cur)
}
}
return dpCitys.sort((a, b) => a - b).join(' ')
}
function uni(arr) {
return [...new Set(arr)]
}
function dfs(start, set = new Set(), res = []) {
res.push(start.value)
set.add(start)
let next = start.next.filter(v => !set.has(v))
next.forEach((v, i) => {
dfs(v, set, res)
// 每次遍历一个元素就将该元素加入一个数组,遍历完后再将这个元素加入一遍,
// 这样我们通过该元素分割时就可以拿到切断该元素后的相连的节点。
res.push(start.value)
})
return res
}
console.log(getDP(`5
1 2
2 3
3 4
4 5`))
console.log(getDP(`6
1 2
2 3
2 4
4 5
4 6
`))