什么是建模?
- 问题------>数据------>模型------>结论
统计建模的本质
收集、分析、展示、解释数据
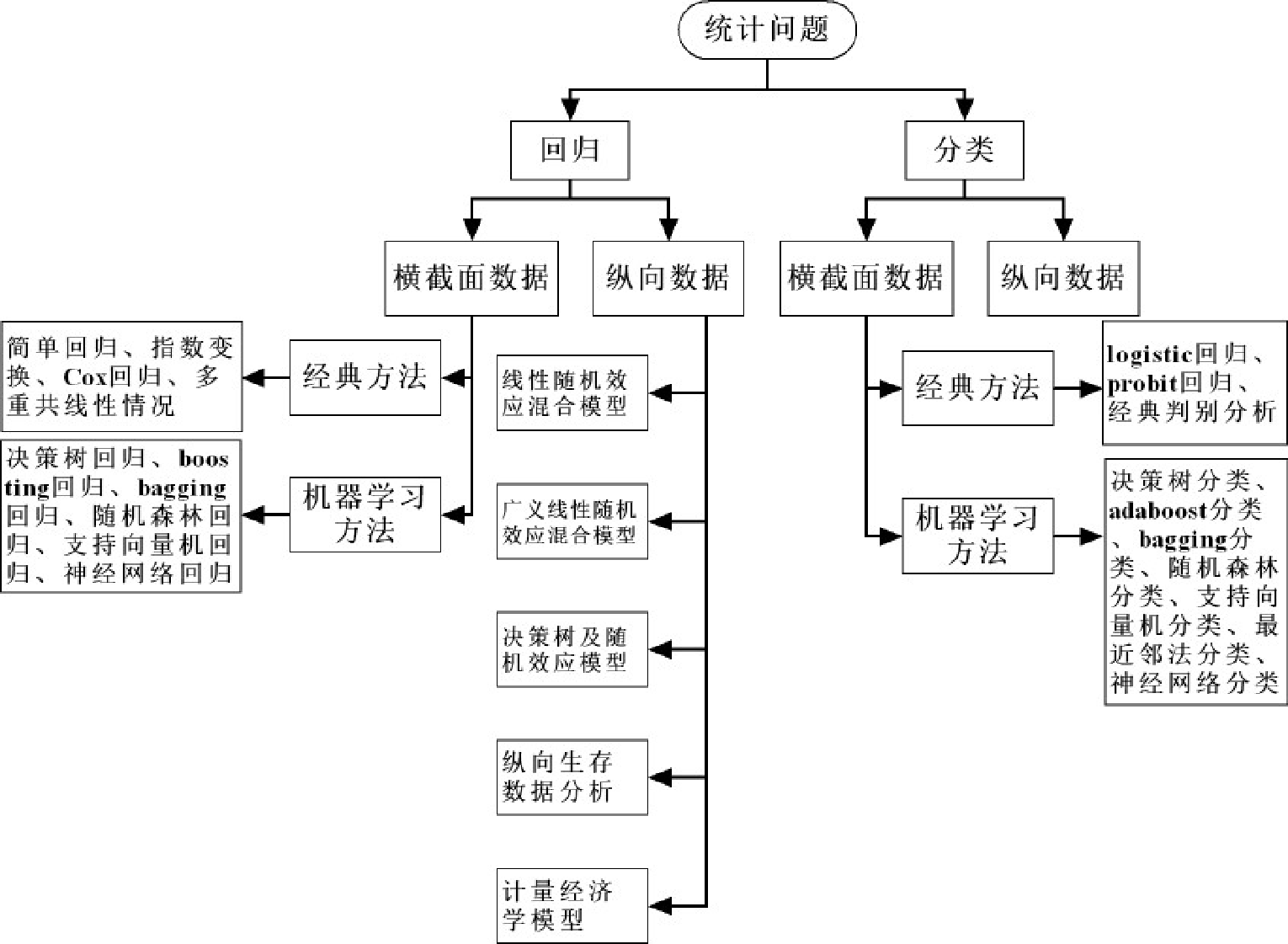
统计问题
- 回归:
横截面数据、纵向数据 - 分类:
横截面数据、分类数据 - 我们观测不到真值,观测到的数据一定有误差。
如何确定模型?
1.根据探索性数据分析主观确定一个参数模型或者一个算法。
2.根据已知数据训练/学习出参数或者算法模型的程序。
模型是被训练出来的
注意:
1.统计方法不能单独使用,必须有问题的背景在
2.统计指标如果显著,不能证明模型正确,但统计指标不显著,则能证明模型错误。例如:某海滩上溺水死亡的人与冰激凌的销量正相关,但他们之间不能简单的划等号。必须有背景在。
在例如:公鸡打鸣太阳上升,注意因果关系与相关关系。建模时不能再没有任何理论依据,背景等的情况下设置假设变量。要根据文献,尊重事件的本质规律。
纵向数据
在计量经济学中普遍存在。空间溢出效应,经济发展的空间溢出效应是指由具有时间和空间特征的区域间要素流动及其衍生的文化扩散及制度环境演化导致的地区经济活动状态和效率发生变化的现象,当一个地区经济发展对另一地区有利时称为正的溢出效应,反之则是负向溢出。
分类问题
去医院看病就是一个分类问题,就是医生在对我们的病进行归类。
奖学金评定也是分类问题。
考古学也是分类问题。
参数模型
所有模型都是错的,但是有一些模型是有用的。
算法模型
一定能算。
没有任何模型假设,也就没有模型假设的错误。好算,快。
与统计模型相比,黑匣子问题。
- 可以两者结合使用,相互验证。
R软件英文参考资料
1.Vincent Zoonekynd编写的Statistics with R
2.Modern Applied Statistics with S
国内统计教学课本的若干误区
假设检验的错误:不能拒绝就接受
当P值被认为不够小而不能拒绝原假设时,只能说"目前没有足够证据拒绝原假设",而不能说是"接受原假设"
P值小于0.05即显著
p值是由一个样本算出来的,不能对其含义夸大或过分理解
置信区间问题
如果根据公式
\[\bar{x}\pm t_{\alpha/2}*\frac{s}{\sqrt{n}} \]
算出来\(\mu\)的置信区间是\([a,b]\),**也不能说区间[a,b]以概率 1 -\\alpha覆盖\\mu**
只能说对于无穷多个不同样本,根据公式算出来无穷多个区间中大概有\(1-\alpha\)比例的置信区间覆盖\(\mu\).
置信区间的前提是样本服从独立正态同分布的。
大样本,小样本
n>30即为大样本的定义是荒唐的,该界限不好确定。
汇总数据与原始数据
能用原始观测数据就不要用汇总数据了,汇总数据会丢失一些东西。