AAAAAAAAAAAAAAAAAAAAA
-----------------------------题解-------------------------------------------
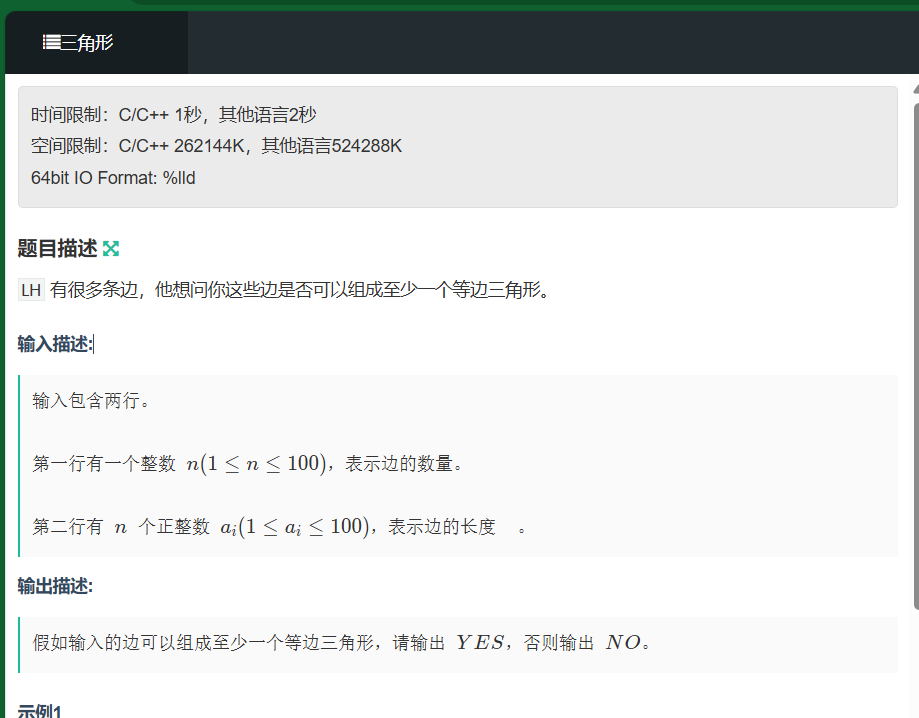
统计数组中有没有出现三个相同的边即可
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int main()
{
int n;
cin>>n;
map<int,int>m;
int jud=0;
for(int i=1;i<=n;i++)
{
int x;
cin>>x;
m[x]++;
if(m[x]>=3) jud=1;
}
if(jud==1) cout<<"YES"<<endl;
else cout<<"NO";
}B.好数组
------------------------题解---------------------------------
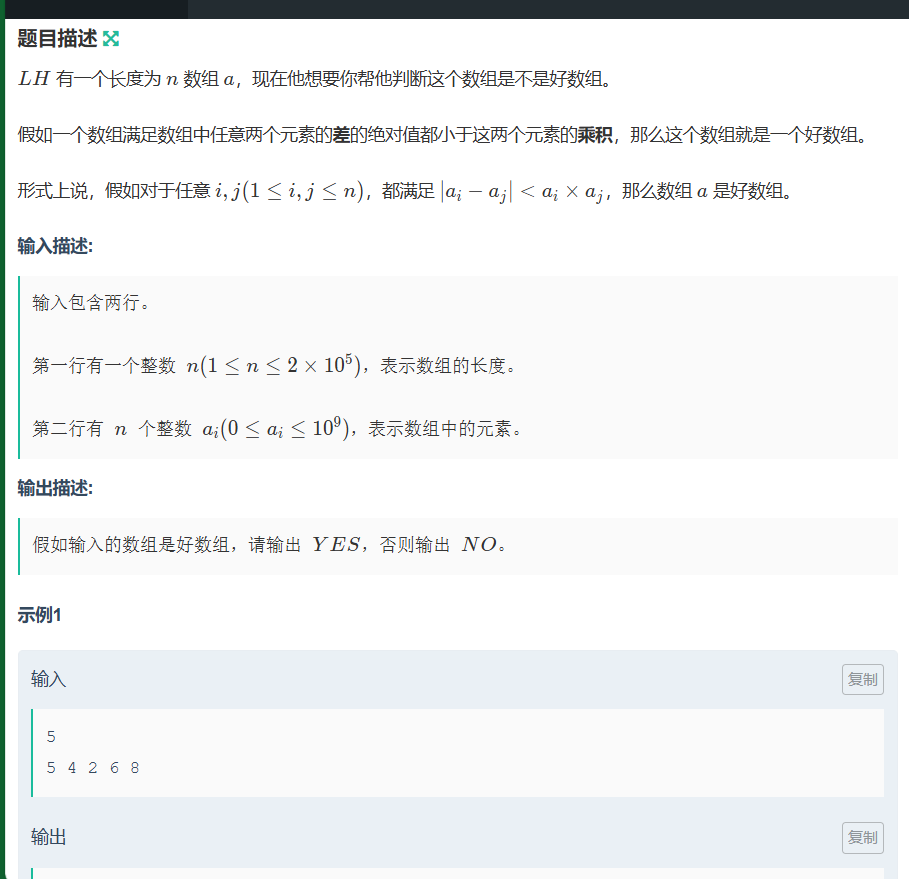
开始想用O1并且特判所有特殊情况,后来发现不行。便开始认真读题,我们可以忽略正负发现一个普遍的规律,还记得基本不的等吗,两个数字相差越小,他们的乘积就越大,那我们只要知道这一个数组最小的乘积看他是否大于他俩的差的绝对值就好了
于是我们sort 一下比较 a[1]和a[n]的差与他俩的乘积就行了
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=2e5+10;
typedef long long ll;
ll a[N];
int main()
{
ll n;
cin>>n;
ll jud=0;
ll c1=0,c2=0;
map<ll,ll>m;
for(ll i=1;i<=n;i++)
{ cin>>a[i];
m[a[i]]++;
}
sort(a+1,a+1+n);
if(abs(a[n]-a[1])<a[1]*a[n]) jud=0;
else jud=1;
if(jud==1) cout<<"NO"<<endl;
else cout<<"YES"<<endl;
}C 前缀平方和序列
-----------------------------题解----------------------------------
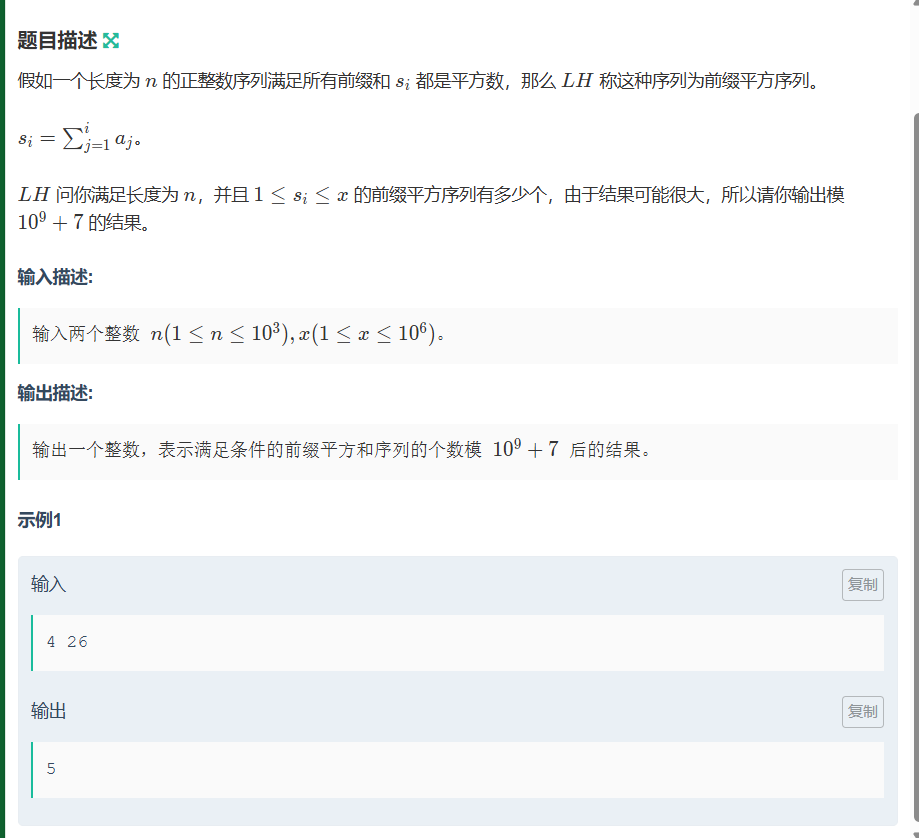
首先要读懂题意,他问的是前缀平方和的序列有多少,而不是能组成这个前缀平方和的数组有多少个(这样的话会是无限个)
读懂之后就很简单了,我们只需要知道x开平方后是多少就可以知道 这个序列最大的长度是多少 比如样例中sqrt(26)=5 那么这个序列最长可以有5个
然后n便是子序列的长度,因此我们可以翻译为 找长度为sqrt(x)的序列的 长度为n的子序列有多少个,直接套用求组和数的板子便可以无脑做出
点击查看代码
#include<bits/stdc++.h>
using namespace std;
const int N=1e6;
typedef long long ll;
const int mod=1e9+7;
ll c[2010][2010];
void init()
{
for(int i=0;i<2010;i++)
{
for(int j=0;j<=i;j++)
{
if(j==0) c[i][j]=1;
else c[i][j]=(c[i-1][j]+c[i-1][j-1])%mod;
}
}
}
ll a[N];
int main()
{ init();
map<ll,ll>m;
ll n,x;
cin>>n>>x;
ll x1=sqrt(x);
cout<<c[x1][n];
}D 走一个大整数迷宫

能看到这里的都是糕手了,我简化语言
-------------------------------------题解-----------------------------------
这题看着很复杂,其实是唬人的,我们仔细阅读那个公式之后就会发现他的后半部分p的二次方什么b[i][j]完全没用,因为你不管是P的多少次方对p-1取模 永远不会等于0
因此这题只与a[i][j]有关
然后就是考验码力的bfs 把所有对a[i][j]取模之后所获得的数字都表达出来,因此开了一个三维数组 ,记录所有路径取模之后的数字。
点击查看代码
#include<bits/stdc++.h>
using namespace std;
int a[20][20];
int b[20][20];
int f[20][20][10010];
bool vis[20][20][10010];
int n,m;
struct node
{
int x,y,sum;
};
int dx[4]={1,0,-1,0};
int dy[4]={0,-1,0,1};
int main()
{ int n,m,p;
cin>>n>>m>>p;
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cin>>a[i][j];
}
for(int i=1;i<=n;i++)
{
for(int j=1;j<=m;j++) cin>>b[i][j];
}
p=p-1;
vis[1][1][a[1][1]%p]=true;
f[1][1][a[1][1]%p]=0;
queue<node> q;
q.push({1,1,a[1][1]%p});
while(q.size())
{
auto u=q.front();
q.pop();
for(int i=0;i<4;i++)
{
int tx=u.x+dx[i],ty=u.y+dy[i];
int sum1=(u.sum+a[tx][ty])%p;
if(tx>=1&&tx<=n&&ty>=1&&ty<=m&&vis[tx][ty][sum1]==false)
{
vis[tx][ty][sum1]=true;
f[tx][ty][sum1]=1+f[u.x][u.y][u.sum];
q.push({tx,ty,sum1});
// cout<<tx<<" "<<ty<<endl;
}
}
}
if(vis[n][m][0]==0) cout<<"-1";
else cout<<f[n][m][0];
}