巨简单！弄懂递归的原理-带括号加法题而已

递归的讲解一大堆，想要明白其中关键又不得其要，让人头疼。我想写一种让我自己让你能简单理解，直扼要命的方式理解**"代码"与"方法"之间的联系**。

1.问题：斐波那契（求和运算）

求4之前的数的总和

2.解决问题的方法

斐波那契数列示例（数值为：1、1、2、3、5、8、13、21、34......在数学上，这一数列以递推的方法定义：F(0)=0，F(1)=1, F(n)=F(n - 1)+F(n - 2)（n ≥ 2，n ∈ N*））

简单理解公式可写出，总和= (1+ ( 2+( 3+4)))

3.代码实现

3.1递归代码实现

复制代码

1 def digui(n):
2     if n == 0:  # 基准情况（边界条件）
3         return 0
4     else:
5         return n + digui(n-1)  # 递归步骤，函数：递，return：归
6 print(digui(4))

代码结果输出：10

"递归"第5行代码这里你把它想成带括号的数学题，有括号先算括号内，直到没有括号，括号内的运算后的值在再与括号外的值运算，如图所示

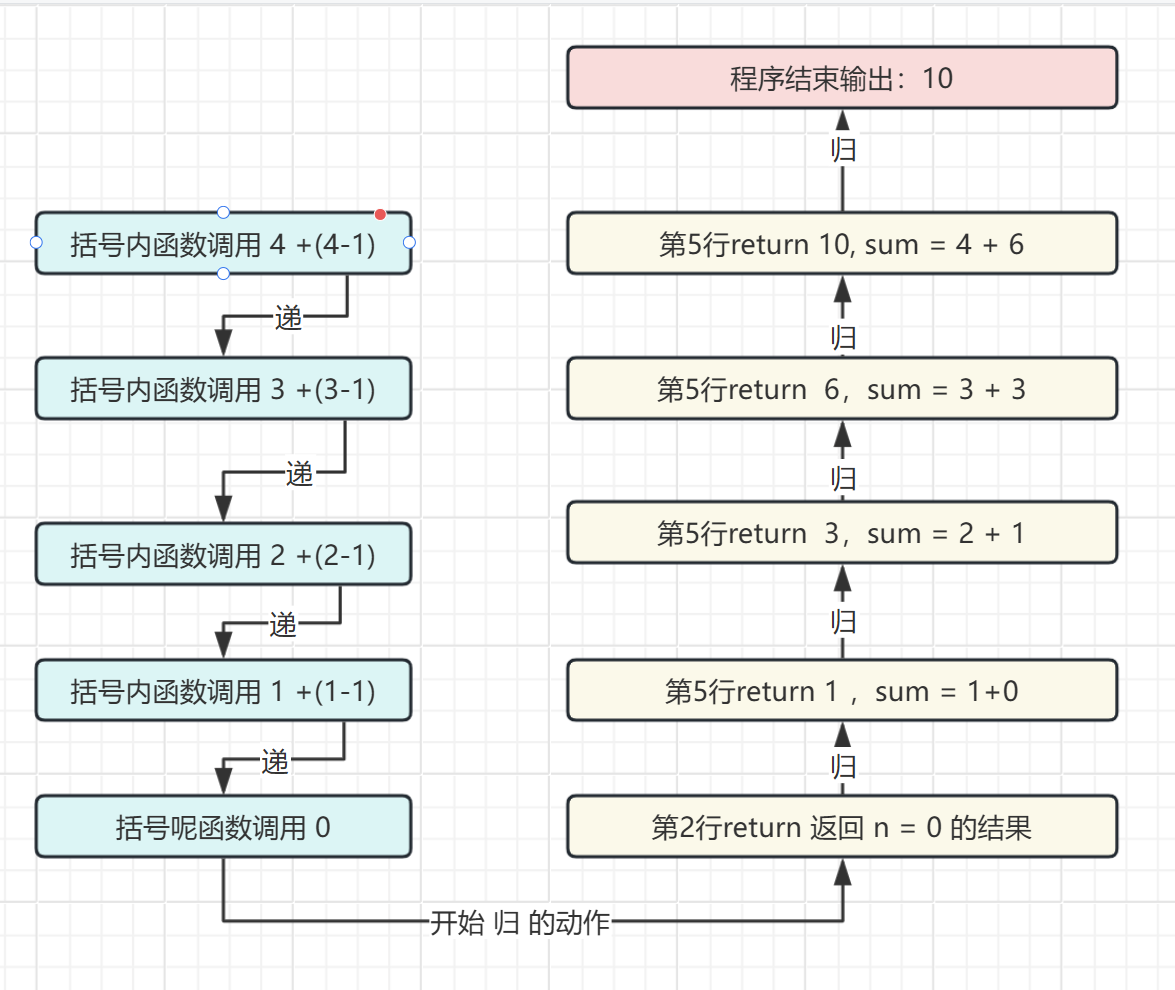
若是用栈表示这段代码就是这个样子，如图所示

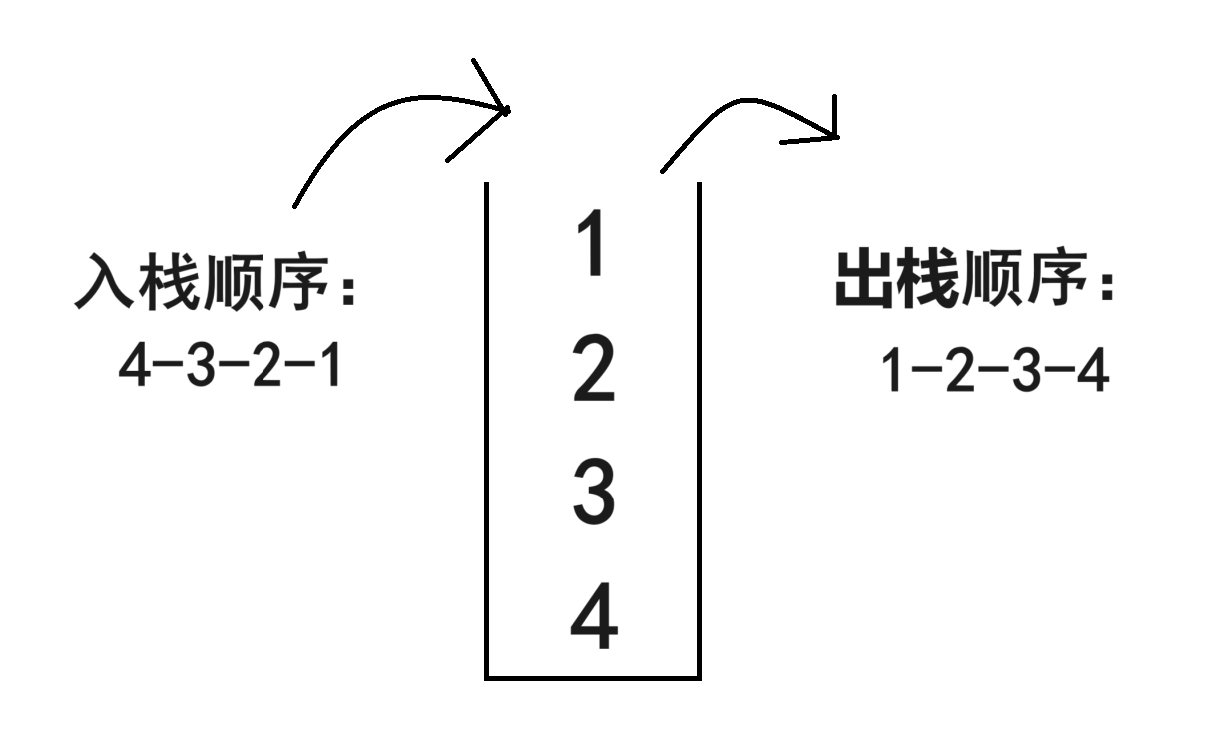
栈的存储顺序：

在每次递归调用的过程中，栈中的内容会是这样的：

复制代码

1 |         |  <- 栈顶（Top of Stack）
2 |  digui(0)  |  <- 这个函数执行完毕并返回 0
3 |  digui(1)  |  <- 1 + digui(0)
4 |  digui(2)  |  <- 2 + digui(1)
5 |  digui(3)  |  <- 3 + digui(2)
6 |  digui(4)  |  <- 4 + digui(3)

3.2循环代码实现

复制代码

1 def xunhuan(n):
2     result = 0
3     for i in range(1, n+1):  # 从 1 到 n 进行循环累加
4         result += i
5     return result
6 
7 print(xunhuan(4))

代码结果输出：10