栈

1.栈的基本概念及描述

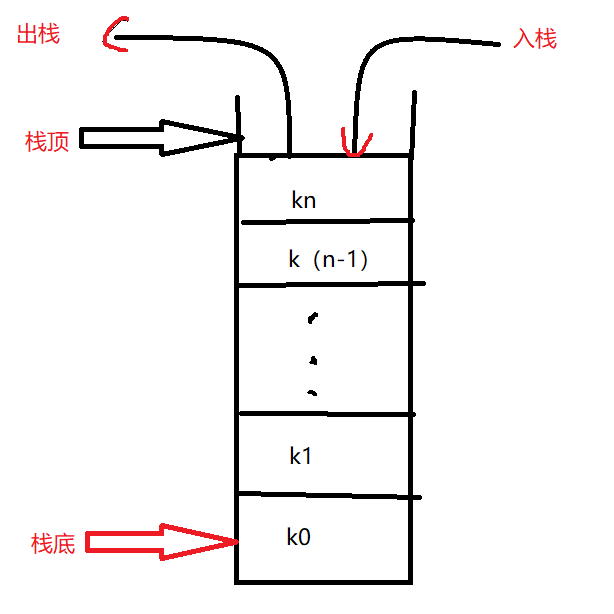
栈是一种特殊的线性表，规定它的插入运算均在线性表的同一端进行，进行插入和删除操作的那一端叫做栈顶，另一端叫做栈底，栈的插入操作叫做入栈,栈的删除操作叫做出栈。

2.顺序栈及其实现

栈的实现方式也有两种：顺序存储 和链式存储 ，分别对应顺序栈和链式栈。

顺序栈是特殊的线性表，它的插入和删除操作在同一端进行，所以也可以使用一维数组来表示。

栈又分为静态栈和动态栈，静态栈定长，不实用，这里我们实现动态栈。数组中下标元素为0就是栈底，对于栈顶，可以使用整型变量top来记录栈顶，top就是下一个元素将要插入结点的存储位置，这样，当top=0时就表示一个空栈。

2.1栈的基本操作

（1）初始化和销毁

c 复制代码

void Init(Stack* st)
{
	st->a = NULL;
	st->capacity = st->top = 0;
}
void Destroy(Stack* st)
{
	if (st->a)
	{
		free(st->a);
		st->a = NULL;
		st->capacity = st->top = 0;
	}
}

（2）入栈

c 复制代码

void Push(Stack* st, datatype x)
{
	assert(st);
	if (st->top == st->capacity)
	{
		int newcapacity = st->capacity == 0 ? 4 : 2 * st->capacity;
		datatype* tmp = (datatype*)realloc(st->a,newcapacity * sizeof(datatype));
		if (tmp == NULL)
		{
			perror("realloc fail");
		}
		st->a = tmp;
        st->capacity=newcapacity;
	}
	st->a[st->top] = x;
	st->top++;
}

（3）出栈

c 复制代码

void Pop(Stack* st)
{
	assert(st);
	assert(st->top > 0);
	st->top--;
}

（4）取栈顶元素

c 复制代码

datatype Top(Stack* st)
{
	assert(st);
	return st->a[st->top-1];
}

（5）栈的元素个数

c 复制代码

int Size(Stack* st)
{
	assert(st);
	return st->top;
}

（6）判空

c 复制代码

bool Empty(Stack* st)
{
	assert(st);
	return st->top == 0;
}

3.栈的应用

3.1 括号匹配

https://leetcode.cn/problems/valid-parentheses/

设一个表达式中可以包含三种括号：大括号、中括号和小括号。各种括号之间可以任意嵌套，但是不能交叉

({}[]) 正确

（{[]}）正确

{[({})]} 正确

{[(]))]} 错误

算法:

自左向右扫描一个字符串，遇到开括号时将其压入栈中，继续扫描下一个字符;
若遇到闭括号时，取栈顶元素与其匹配，若匹配,删除栈顶元素，继续；
扫描结束后，若栈为空，括号匹配；
若栈不为空，括号就不匹配。

c 复制代码

bool isValid(char* s)
{
    Stack st;
    Init(&st);
    while (*s) {
        if (*s == '(' || *s == '{' || *s == '[') {
            Push(&st, *s);
        } else {
            if (Empty(&st)) {
                Destroy(&st);
                return false;
            }

            char p = Top(&st);
            Pop(&st);
            if (p == '(' && *s != ')' || p == '[' && *s != ']' ||
                p == '{' && *s != '}') {
                Destroy(&st);
                return false;
            }
        }
        ++s;
    }
    bool ret = Empty(&st);
    Destroy(&st);
    return ret;
}

3.2后缀表达式

后缀表达式中没有括号，操作符在操作数之后，按照从左往右的顺序执行操作，每遇到一个操作符，将前面两个操作数执行相应的操作。

后缀表达式	中缀表达式
3 5 2 * -	3-（5*2）
3 5 - 2 *	（3-5）*2
3 5 2 *1 + /	3/（2*5+1）

算法:

从左向右扫描中缀表达式中的每个字符，如果遇到数字字符和圆点".",直接将其写入后缀表达式中
如果遇到的时开括号，将它压入一个操作符栈中，在遇到匹配的闭括号时，将栈中的元素弹出放入后缀表达式，知道栈顶元素为开括号时，将栈顶元素"（"弹出；
如果遇到的是操作符，将该操作符与操作符栈顶元素进行比较

（1）当所遇到的操作符的优先级小于或等于栈顶元素的优先级时，取出栈顶元素放入后缀表达式，并弹出该栈顶元素，反复执行到栈顶元素的优先级小于当前操作符的优先级

（2）当遇到的操作符的优先级大于栈顶元素的优先级时将它压入栈中。