详解池化层
除了卷积层,卷积网络也经常使用池化层来缩减模型的大小,提高计算速度,同时提高所提取特征的鲁棒性,来看一下。
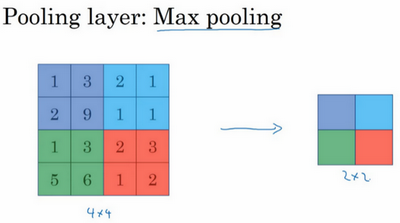
先举一个池化层的例子,然后再讨论池化层的必要性。假如输入是一个4×4矩阵,用到的池化类型是最大池化(max pooling)。执行最大池化的树池是一个2×2矩阵。执行过程非常简单,把4×4的输入拆分成不同的区域,把这个区域用不同颜色来标记。对于2×2的输出,输出的每个元素都是其对应颜色区域中的最大元素值。
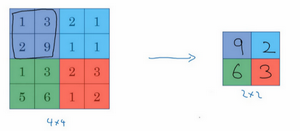
左上区域的最大值是9,右上区域的最大元素值是2,左下区域的最大值是6,右下区域的最大值是3。为了计算出右侧这4个元素值,需要对输入矩阵的2×2区域做最大值运算。这就像是应用了一个规模为2的过滤器,因为选用的是2×2区域,步幅是2,这些就是最大池化的超参数。
因为使用的过滤器为2×2,最后输出是9。然后向右移动2个步幅,计算出最大值2。然后是第二行,向下移动2步得到最大值6。最后向右移动3步,得到最大值3。这是一个2×2矩阵,即\(f=2\),步幅是2,即\(s=2\)。
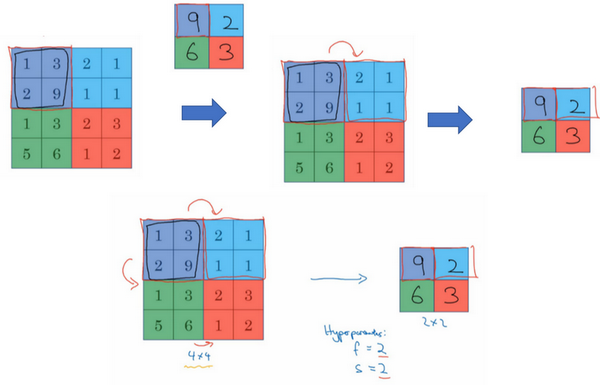
这是对最大池化功能的直观理解,可以把这个4×4输入看作是某些特征的集合,也许不是。可以把这个4×4区域看作是某些特征的集合,也就是神经网络中某一层的非激活值集合。数字大意味着可能探测到了某些特定的特征,左上象限具有的特征可能是一个垂直边缘,一只眼睛,或是大家害怕遇到的CAP特征。显然左上象限中存在这个特征,这个特征可能是一只猫眼探测器。然而,右上象限并不存在这个特征。最大化操作的功能就是只要在任何一个象限内提取到某个特征,它都会保留在最大化的池化输出里。所以最大化运算的实际作用就是,如果在过滤器中提取到某个特征,那么保留其最大值。如果没有提取到这个特征,可能在右上象限中不存在这个特征,那么其中的最大值也还是很小,这就是最大池化的直观理解。
必须承认,人们使用最大池化的主要原因是此方法在很多实验中效果都很好。尽管刚刚描述的直观理解经常被引用,不知大家是否完全理解它的真正原因,不知大家是否理解最大池化效率很高的真正原因。
其中一个有意思的特点就是,它有一组超参数,但并没有参数需要学习。实际上,梯度下降没有什么可学的,一旦确定了\(f\)和\(s\),它就是一个固定运算,梯度下降无需改变任何值。
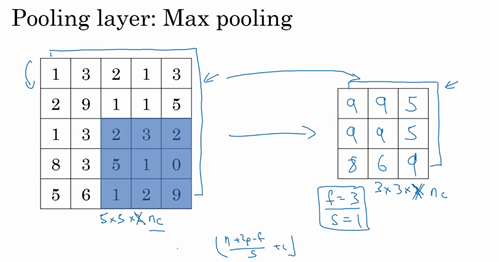
来看一个有若干个超级参数的示例,输入是一个5×5的矩阵。采用最大池化法,它的过滤器参数为3×3,即\(f=3\),步幅为1,\(s=1\),输出矩阵是3×3.之前讲的计算卷积层输出大小的公式同样适用于最大池化,即\(\frac{n + 2p - f}{s} + 1\),这个公式也可以计算最大池化的输出大小。
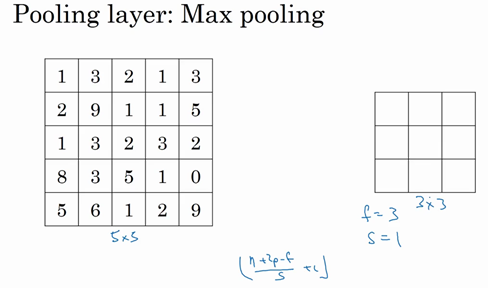
此例是计算3×3输出的每个元素,看左上角这些元素,注意这是一个3×3区域,因为有3个过滤器,取最大值9。然后移动一个元素,因为步幅是1,蓝色区域的最大值是9.继续向右移动,蓝色区域的最大值是5。然后移到下一行,因为步幅是1,只向下移动一个格,所以该区域的最大值是9。这个区域也是9。这两个区域的最大值都是5。最后这三个区域的最大值分别为8,6和9。超参数\(f=3\),\(s=1\),最终输出如图所示。
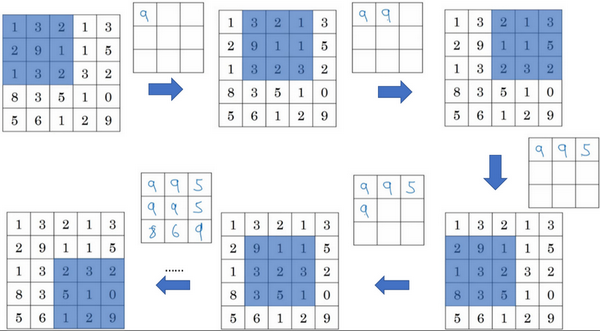
以上就是一个二维输入的最大池化的演示,如果输入是三维的,那么输出也是三维的。例如,输入是5×5×2,那么输出是3×3×2。计算最大池化的方法就是分别对每个通道执行刚刚的计算过程。如上图所示,第一个通道依然保持不变。对于第二个通道,我刚才画在下面的,在这个层做同样的计算,得到第二个通道的输出。一般来说,如果输入是5×5×\(n_{c}\),输出就是3×3×\(n_{c}\),\(n_{c}\)个通道中每个通道都单独执行最大池化计算,以上就是最大池化算法。
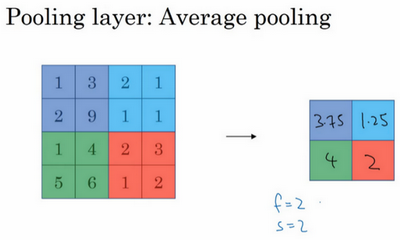
另外还有一种类型的池化,平均池化,它不太常用。我简单介绍一下,这种运算顾名思义,选取的不是每个过滤器的最大值,而是平均值。示例中,紫色区域的平均值是3.75,后面依次是1.25、4和2。这个平均池化的超级参数\(f=2\),\(s=2\),也可以选择其它超级参数。
目前来说,最大池化比平均池化更常用。但也有例外,就是深度很深的神经网络,可以用平均池化来分解规模为7×7×1000的网络的表示层,在整个空间内求平均值,得到1×1×1000,一会看个例子。但在神经网络中,最大池化要比平均池化用得更多。
总结一下,池化的超级参数包括过滤器大小\(f\)和步幅\(s\),常用的参数值为\(f=2\),\(s=2\),应用频率非常高,其效果相当于高度和宽度缩减一半。也有使用\(f=3\),\(s=2\)的情况。至于其它超级参数就要看用的是最大池化还是平均池化了。也可以根据自己意愿增加表示padding 的其他超级参数,虽然很少这么用。最大池化时,往往很少用到超参数padding 。大部分情况下,最大池化很少用padding 。目前\(p\)最常用的值是0,即\(p=0\)。最大池化的输入就是\(n_{H} \times n_{W} \times n_{c}\),假设没有padding ,则输出\(\lfloor\frac{n_{H} - f}{s} +1\rfloor \times \lfloor\frac{n_{w} - f}{s} + 1\rfloor \times n_{c}\)。输入通道与输出通道个数相同,因为对每个通道都做了池化。需要注意的一点是,池化过程中没有需要学习的参数。执行反向传播时,反向传播没有参数适用于最大池化。只有这些设置过的超参数,可能是手动设置的,也可能是通过交叉验证设置的。
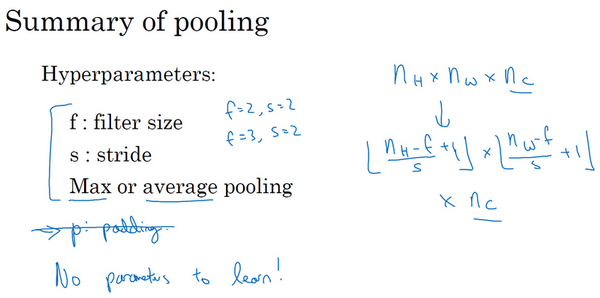
除了这些,池化的内容就全部写完了。