一 问题引入
在高一学函数性质时,我们会遇到一些抽象函数的问题,先看两道例题:
【例1】 已知函数\(f\left(2x+1\right)\)的定义域为\(\left[1,2\right]\),则函数\(f\left(4x+1\right)\)的定义域是 .
【例2】 已知函数\(f\left(x\right)\)的定义域为\(\mathrm{R}\),且\(f\left(2x-1\right)\)的图象关于直线\(x=1\)对称,\(f\left(3x+2\right)\)是奇函数,则下列选项中值一定为\(0\)的是( )
A.\(f\left(\frac{7}{2}\right)\) B.\(f\left(2024\right)\) C.\(f\left(1\right)\) D.\(f\left(\frac{3}{2}\right)\)
以上两题中没告知函数解析式,我们可以利用函数图象变换的方法处理类似的问题.
二 图象变换
图象变换包括平移变换、伸缩变换、对称变换和翻转变换,我们只需了解前两种变换.
(等我们学了必修第一册第五章三角函数会有更好的理解)
回忆下,我们刚学一次函数\(y=kx+b(k\neq0)\)时,是如何知道图象是一直线的呢?
就是"列表---描点---连线"!
1 平移变换
我们知道平移变换口诀:左加右减,上加下减,
Eg1:\(y=f(x)\)向左平移\(1\)个单位,向下平移\(2\)个单位后的函数是\(y=f(x+1)-2\);
Eg2:\(y=f(2x-4)\)向左平移\(1\)个单位后的函数是\(y=f[2(x+1)-4]=f(2x-2)\);
为什么不是\(y=f(2x+1-4)=f(2x-3)\)?
用描点的方式了解下(不太严谨),
角度1
假设\(y=f\left(2x-4\right)\)是\(y=2x-4\),其图象向左平移\(1\)个单位后,如下图显然平移变换后的函数是\(y=2x-2\).
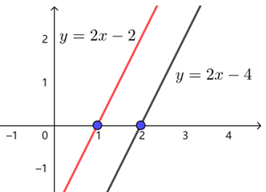
角度2
若点\((x_0,y_0)\)在\(y=f(2x-4)\)图象上,则\(y_0=f(2x_0-4)\);而点\((x_0,y_0)\)经过平移变换"向左平移\(1\)个单位"后是\((x_0-1,y_0)\),显然点\((x_0-1,y_0)\)在\(y=f(2x-2)\)图象上而不是\(y=f(2x-3)\).
简而言之,"左加右减"是对\(x\)进行加减,\(y=f[2(x+1)-4]\)中的小括号不能不要.
2 伸缩变换
\(y=f(x)\)的图象要伸缩变换:纵坐标\(y\)不变横坐标\(x\)扩大\(2\)倍,即\((x,y)\)会变成\((2x,y)\),它的解析式会是什么?
用具体例子感受下,
\(y=x^2\)经过伸缩变换:纵坐标\(y\)不变横坐标\(x\)扩大\(2\)倍,点\(A(1,1)\)到点\(B(2,1)\);
点\((x_0,y_0)\)在\(y=x^2\)图象上,则\(y_0={x_0}^2\),变换后对应的点\((x_1,y_1)\),有\(\left\{\begin{array}{l} x_1=2 x_0 \\ y_1=y_0 \end{array}\right.\),
则\(\left\{\begin{array}{l} x_0=\dfrac{x_1}{2} \\ y_0=y_1 \end{array}\right.\),所以\(y_1={\left(\frac{x_1}{2}\right)}^2=\frac{x_1^2}{4}\),故变换后的函数解析式为\(y=\frac{x^2}{4}\).
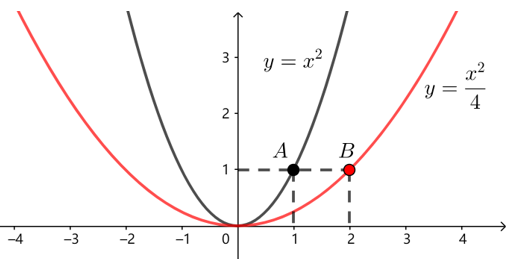
若\(y=x^2\)经过伸缩变换:纵坐标\(y\)不变横坐标\(x\)缩小到原来的\(\frac{1}{2}\),点\((1,1)\)到点\((2,1)\);
变换后的函数解析式为\(y={(2x)}^2=4x^2\).
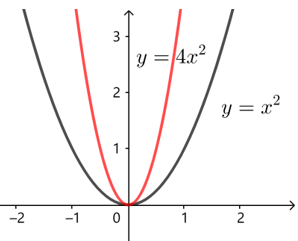
简而言之,将\(y=f(x)\)的图象上各点的横坐标伸长\((0<b<1)\)或缩短\((b>1)\)到原来的\(\frac{1}{b}\)倍,而纵坐标不变,得到函数\(y=f(bx)\)的图象.
若将\(y=f(x)\)的图象上各点的纵坐标伸长\((a>1)\)或缩短\((0<a<1)\)到原来的\(a\)倍,而横坐标不变,得到函数\(y=af(x)\)的图象.
三 图象变换的逆运用
我们知道了函数图象经过平移变换或伸缩变换后函数解析式的变换.
那函数\(y=f(2x-2)\)如何变换后变成函数\(y=f(x)\)呢?
方法1 先平移后伸缩
\(y=f(2x-2)=f[2(x-1)]\)向左平移\(1\)个单位得到\(y=f(2x)\),再横坐标\(x\)扩大\(2\)倍得到\(y=f(x)\).
方法2 先伸缩后平移
\(y=f(2x-2)\)横坐标\(x\)扩大\(2\)倍得到\(y=f(x-2)\),再向左平移\(2\)个单位得到\(y=f(x)\).
四 问题的解决
我们了解了以上两点,现在试试如何解决一开始提出的两个问题,
【例1】 已知函数\(f\left(\frac{x}{2}+1\right)\)的定义域为\(\left[-1,2\right]\),则函数\(f\left(2x+1\right)\)的定义域是 .
解 利用图象变换求解,
函数\(f\left(\frac{x}{2}+1\right)=f\left[\frac{1}{2}\left(x+2\right)\right]\)的定义域为\(\left[-1,2\right]\)
\\stackrel {向右平移2个单位}{\\Longrightarrow} f\\left(\\frac{x}{2}\\right)\\(的定义域为\\)\[1,4\]
\\stackrel {横坐标缩小到原来的\\frac{1}{4}}{\\Longrightarrow} f\\left(2x\\right)\\(的定义域为\\)\\left\[\\frac{1}{4},1\\right\]
\\stackrel {向左平移\\frac{1}{2}个单位}{\\Longrightarrow} f\\left(2x\\right)\\(的定义域为\\)\\left\[-\\frac{1}{4},\\frac{1}{2}\\right\]
故答案为\(\left[-\frac{1}{4},\frac{1}{2}\right]\).
【例2】 已知函数\(f\left(x\right)\)的定义域为\(\mathrm{R}\),且\(f\left(2x-1\right)\)的图象关于直线\(x=1\)对称,\(f\left(3x+2\right)\)是奇函数,则下列选项中值一定为\(0\)的是( )
A.\(f\left(\frac{7}{2}\right)\) B.\(f\left(2024\right)\) C.\(f\left(1\right)\) D.\(f\left(\frac{3}{2}\right)\)
解 由的图象关于直线\(x=1\)对称
\\stackrel {向左平移\\frac{1}{2}个单位}{\\Longrightarrow} f\\left(2x\\right)\\(的图象关于直线\\)x=\\frac{1}{2}\\(对称 \\)\\stackrel {横坐标扩大2倍}{\\Longrightarrow} f\\left(x\\right)\\(的图象关于直线\\)x=1对称
由\(f\left(3x+2\right)\)是奇函数,关于\((0,0)\)对称
\\stackrel {向右平移\\frac{2}{3}个单位}{\\Longrightarrow} f\\left(3x\\right)\\(的图象关于\\)\\left(\\frac{2}{3},0\\right)\\(对称 \\)\\stackrel {横坐标扩大3倍}{\\Longrightarrow} f\\left(x\\right)\\(的图象关于\\)(2,0)对称
则\(f\left(x\right)\)的图象关于直线\(x=1\)对称,且关于\((2,0)\)对称,
假设当\(0<x<1\)时,\(y=x\),反复使用以上两点,结合图象可得函数\(f\left(x\right)\)周期为\(4\).
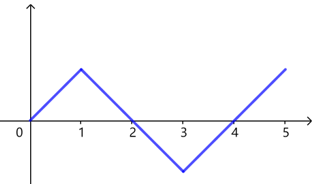
则\(f\left(2024\right)=f(0)=0\).
\(f\left(\frac{7}{2}\right)=f\left(-\frac{1}{2}\right)=-f\left(\frac{3}{2}\right)\),\(f\left(1\right)\)都不确定是否为\(0\).
故选:\(B\).
问题的另解
【例1】 因为函数\(f\left(\frac{x}{2}+1\right)\)的定义域为\(\left[-1,2\right]\),即\(x\in\left[-1,2\right]\),所以\(\frac{x}{2}+1\in\left[\frac{1}{2},2\right]\),
由\(\frac{1}{2}\le2x+1\le2\)解得\(-\frac{1}{4}\le x\le\frac{1}{2}\),
所以函数\(f\left(4x+1\right)\)的定义域为\(\left[-\frac{1}{4},\frac{1}{2}\right]\).
【例2】 \(f\left(2x-1\right)\)的图象关于直线\(x=1\)对称,
则\(f\left(2x-1\right)=f\left(2(-x+2)-1\right)=f(-2x+3)\).
即\(f\left(2x-1\right)=f\left(2(-x+2)-1\right)=f(-(2x-1)+2)\),
令\(t=2x-1\),则\(f\left(t\right)=f(-t+2)\),
则\(f\left(x\right)\)也关于\(x=1\)对称.
\(f\left(3x+2\right)\)是奇函数,
则\(f\left(3x+2\right)+f(-3x+2)=0\),\(f\left(3x+2\right)+f(-(3x+2)+4)=0\),
令\(t=3x+2\),则\(f\left(t\right)+f(-t+4)=0\),则\(f\left(x\right)\)也关于\((2,0)\)对称.
且令\(t=2\),得\(f(2)=0\).
由前面知道\(f\left(t\right)=f(-t+2)=-f(-t+4)\),且令\(t=0\),则\(f(0)=f(2)=f(4)=0\).
且\(f(-t+2)=-f(-t+4)=-(-f(-t+6))=f(-t+6)\),
令\(m=-t+2\),则\(f(m)=f(m+4)\),
故\(f\left(x\right)\)周期为\(4\).
则\(f\left(2024\right)=f(0)=0\).
\(f\left(\frac{7}{2}\right)=f\left(-\frac{1}{2}\right)=-f\left(\frac{3}{2}\right)\),\(f\left(1\right)\),都不确定是否为\(0\).
故选:\(B\).
五 巩固练习
-
已知函数\(f\left(2x-1\right)\)的定义域为\(\left(-1,9\right)\),则函数\(f\left(3x+1\right)\)的定义域为( )
A.\(\left(-\frac{1}{3},\frac{4}{3}\right)\) B.\(\left(-\frac{4}{3},\frac{16}{3}\right)\) C.\(\left(-\frac{2}{3},\frac{8}{3}\right)\) D.\(\left(-2,28\right)\)
-
已知函数\(f\left(x\right)\)对任意的\(x\in R\)都有\(f\left(x+8\right)=-f\left(x\right)\),若\(y=f\left(x+2\right)\)的图象关于点\(\left(-2,0\right)\)对称,且\(f\left(3\right)=3\),则\(f\left(43\right)=\)( )
A.\(0\) B.\(-3\) C.\(3\) D.\(4\)
-
已知函数\(y=f\left(2x-1\right)\)的图象关于点\(\left(-1,1\right)\)对称,则下列函数是奇函数的是( )
A.\(y=f\left(2x-2\right)+1\) B.\(y=f\left(2x-3\right)+1\)
C.\(y=f\left(2x-2\right)-1\) D.\(y=f\left(2x-3\right)-1\)
-
已知\(f\left(x-1\right)\)是定义域为\(R\)的奇函数,\(g\left(x\right)=f\left(2x+3\right)\)是定义域为R的偶函数,则( )
A.\(g\left(2\right)=0\) B.\(g\left(3\right)=0\) C.\(f\left(3\right)=0\) D.\(f\left(5\right)=0\)
-
(多选)已知函数\(f(x)\)的定义域为\(\mathrm{R}\),\(f(x+1)\)为奇函数,\(f(x+2)\)为偶函数,且\(x\in[0,1]\)时,\(f(x)\)单调递增,则下列结论正确的为( )
A.\(f(x)\)是偶函数 B.\(f(x)\)的图象关于点\((-1,0)\)中心对称
C.f(2024)=0 D.\(f\left(\frac{5}{4}\right)+f\left(-\frac{1}{4}\right)<0\)
参考答案
- 【详解】函数\(f\left(2x-1\right)\)的定义域为\(\left(-1,9\right)\),
\\stackrel {向左平移\\frac{1}{2}个单位}{\\Longrightarrow} \\(函数\\)f\\left(2x\\right)\\(的定义域为\\)\\left(-\\frac{3}{2},\\frac{17}{2}\\right)\\(, \\)\\stackrel {横坐标缩小到原来的\\frac{2}{3}倍}{\\Longrightarrow} \\(函数\\)f\\left(3x\\right)\\(的定义域为\\)\\left(-1,\\frac{17}{3}\\right)\\(, \\)\\stackrel {向左平移\\frac{1}{3}个单位}{\\Longrightarrow} \\(函数\\)f\\left(3x+1\\right)\\(的定义域为\\)\\left(-\\frac{4}{3},\\frac{16}{3}\\right)\\(. 故选:\\)B. - 【详解】由于\(y=f\left(x+2\right)\)的图象关于点\((-2,0)\)对称,
故\(y=f\left(x\right)\)的图象关于点\((0,0)\)对称,即\(y=f\left(x\right)\)为奇函数,
又\(f\left(x+8\right)=-f\left(x\right)\),
则\(f\left(x+16\right)=-f\left(x+8\right)=f\left(x\right)\),即16 \\(为\\)f\\left(x\\right)\\(的周期, 令\\)x=-3\\(代入\\)f\\left(x+8\\right)=-f\\left(x\\right)\\(,则\\)f\\left(5\\right)=-f\\left(-3\\right)=f\\left(3\\right)=3\\(, 故\\)f\\left(43\\right)=f\\left(43-3\\times16\\right)=f\\left(-5\\right)=-f\\left(5\\right)=-3\\(, 故选:\\)B - 【详解】函数\(y=f\left(2x-1\right)\)的图象关于点\(\left(-1,1\right)\)对称,
所以函数\(y=f\left(2x-1\right)\)的图象向右平移\(1\)个单位,
向下平移一个单位后函数的图象关于点\(\left(0,0\right)\)对称,
即可得\(y=f\left[2\left(x-1\right)-1\right]-1=f\left(2x-3\right)-1\).
故选:\(D\) - 【详解】因为\(f\left(x-1\right)\)是定义域为\(R\)的奇函数,
所以函数\(f\left(x\right)\)关于点\(\left(-1,0\right)\)对称,且f\\left(-1\\right)=0
因为\(g\left(x\right)=f\left(2x+3\right)\)是定义域为\(R\)的偶函数,
所以函数\(f\left(x\right)\)关于直线\(x=3\)对称,
所以\(f\left(7\right)=0\),即\(g\left(2\right)=0\).
故选:\(A\) - 【详解】因为\(f(x+1)\)为奇函数,所以\(f(x)\)关于\((1,0)\)对称 ①,
因为\(f(x+2)\)为偶函数,所以\(f(x)\)关于\(x=2\)对称 ②,
\(x\in[0,1]\)时,\(f(x)\)单调递增,
假设当\(0\le x\le1\)时,\(y=x-1\),
反复使用以上①②两点,
结合图象可得函数周期为\(T=4\),\(f(x)\)是偶函数,\(f(x)\)的图象关于点\((-1,0)\)中心对称,\(f(2024)=f(0)\)不一定为\(0\).
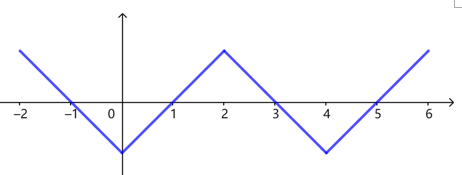
故\(AB\)正确,\(C\)错误;
因为\(f\left(\frac{5}{4}\right)+f\left(-\frac{1}{4}\right)=f\left(2-\frac{3}{4}\right)+f\left(\frac{1}{4}\right)\)\(=-f\left(-\frac{3}{4}\right)+f\left(\frac{1}{4}\right)=f\left(\frac{1}{4}\right)-f\left(\frac{3}{4}\right)\),
且\(x\in[0,1]\)时,\(f(x)\)单调递增,
所以\(f\left(\frac{1}{4}\right)<f\left(\frac{3}{4}\right)\),即\(f\left(\frac{1}{4}\right)-f\left(\frac{3}{4}\right)<0\),
故\(D\)正确.
故选:\(ABD\).