R语言经典统计分析

经典统计分析包括了许多常用的统计方法和技术，用于数据的描述、推断和建模。本节将介绍经典统计分析方法（包括t检验、方差分析、卡方检验、线性回归）在R语言中的实现。

5.1.1 t检验

样本均值（sample mean），又称样本均数，是描述一组数据集中趋势的重要统计量。它是通过将一组数据的所有数值相加后，再除以这组数据的个数来计算的。在统计学中，方差是每个样本值与样本均值之差的平方的平均值。方差衡量了数据的离散程度，即数据点相对于均值的散布情况。标准差则是方差的平方根，表示数据相对于均值的平均偏离程度。标准差也是一种度量数据分散程度的重要指标。

t检验是一种统计方法，用于比较两个样本的均值是否存在显著差异。它基于样本均值和样本标准差，通过计算t值来判断两个样本均值是否显著不同。t检验适用于连续变量的独立样本或配对样本的比较，在医学领域中广泛使用。t检验有两种类型：单样本t检验和双样本t检验。

1. 单样本t检验

单样本t检验的目的是检验单样本的均值是否与已知总体的均值相等。

应用场景举例：在某偏远地区随机抽取若干名健康男子，检验其脉搏均值是否高于全体健康男子的平均水平；检验某一线城市全体高三学生的视力水平是否低于全国高三学生的视力水平。

在R语言中，可以使用t.test函数进行单样本t检验。具体步骤包括：

设置零假设（H0）：假设检验的零假设通常是样本均值等于总体均值。

收集样本数据。

运行单样本t检验：使用t.test函数，指定样本数据和总体均值，得出检验结果，包括t值、p值和置信区间。

2. 双样本t检验

双样本t检验的目的是检验两个独立样本的均值是存在显著差异，要求两样本独立，服从正态分布或近似正态。

应用场景举例：为研究某种治疗儿童贫血的新药的疗效，以常规药作为对照，治疗一段时间后，检验施以新药的儿童的血红蛋白的增加量是否比常规药的大；检验两种药物对治疗高血压的效果，检验两组药物的降压水平是否存在显著差异。

在R语言中，也可以使用t.test函数进行双样本t检验。具体步骤包括：

设置零假设（H0）：假设检验的零假设通常是两个样本的均值相等。

收集两组独立样本数据。

运行双样本t检验：使用t.test函数，指定两个样本数据，得出检验结果，包括t值、p值和置信区间。

在执行t检验时，关键的输出包括t值、自由度、p值和置信区间。p值通常用来判断检验结果的显著性，如果p值小于显著性水平（通常为0.05），则可以拒绝零假设，认为两个样本的均值存在显著差异。执行t检验的示例R代码如下：

复制代码

#单样本t检验

set.seed(123)

blood_pressure <- rnorm(30, mean = 120, sd = 10) #创建数据blood_pressure

#执行单样本t检验，比较样本blood_pressure的均值与总体均数mu=130的差异

t_test_single_blood_pressure <- t.test(blood_pressure, mu = 130)

#输出单样本t检验结果

print(t_test_single_blood_pressure)

#双样本t检验

set.seed(123)

baseline_blood_sugar <- rnorm(20, mean = 100, sd = 15) #创建数据baseline_blood_sugar

endline_blood_sugar <- rnorm(20, mean = 120, sd = 15) #创建数据endline_blood_sugar

#执行双样本t检验，比较样本baseline_blood_sugar和endline_blood_sugar均值的差异

t_test_double_blood_sugar <- t.test(baseline_blood_sugar, endline_blood_sugar)

#输出双样本t检验结果

print(t_test_double_blood_sugar)

运行结果如图5-1所示。该图展示了单样本和双样本t检验的结果，其中p值分别为2.431e-06和0.0003，均小于0.05。结果提示，blood_pressure的均值与总体均数130之间存在显著差异，baseline_blood_sugar与endline_blood_sugar之间均值也存在显著差异，且这种差异具有统计学意义。

图5-1

总的来说，t检验是一种常用的假设检验方法，用于比较样本均值之间的差异。在R语言中，使用t.test函数进行t检验非常方便，能够帮助用户快速、准确地进行显著性检验。

5.1.2 方差分析

方差分析（Analysis of Variance，简称ANOVA），由英国统计学家R.A.Fisher首创，为纪念Fisher故以"F"命名，所以方差分析又称"F检验"。它用于两个及两个以上样本均值差异的显著性检验。

方差分析中使用频率最高的是单因素方差分析。它用于分析一类定类数据与定量数据之间的差异性，且定类数据通常为多分类数据。例如，分析不同班级（1班、2班、3班）学习成绩之间的差异时，可以使用单因素方差分析来比较这3个班级学习成绩均值的差异（独立样本t检验只能进行两组数据之间均值差异的比较）。

在R语言中，可以使用stats包中的aov函数和car包中的Anova函数进行单因素方差分析。具体步骤包括：

设置零假设（H0）：假设检验的零假设通常是所有组的均值相等。

收集各组样本数据。

运行单因素方差分析：使用aov函数指定因变量和组变量，使用summary函数获取方差分析的结果，包括F统计量、自由度和p值。

在方差分析中，关键的输出值为F值和p值。F值用于判断组间均值差异是否显著；当p值小于显著性水平（通常为0.05）时，则可以拒绝零假设，认为组间均值存在显著差异。执行方差分析的示例R代码如下：

复制代码

#创建数据框（包含3个组别的计量资料）

data <- data.frame(

  RecoveryTime = c(10, 12, 8, 9, 11, 14, 13, 7, 6, 5,11), #恢复时间

  Treatment = factor(c("TreatmentA", "TreatmentB", "TreatmentC", "TreatmentA",

                       "TreatmentB", "TreatmentC", "TreatmentA", "TreatmentB",

                       "TreatmentC", "TreatmentA", "TreatmentB")))#治疗方法

#进行方差分析

aov_result <- aov(RecoveryTime ~ Treatment, data = data)

summary(aov_result)

运行结果如图5-2所示，该图展示了方差分析结果，通过summary(aov())计算得出F值为0.116和p值为0.892。p值大于0.05说明治疗方法对恢复时间没有显著影响。

图5-2

总的来说，方差分析是一种常用的统计方法，用于比较组间均值是否有显著差异。在R语言中，使用aov函数和Anova函数进行方差分析非常方便，能够帮助用户快速、准确地进行组间差异比较。

5.1.3 卡方检验

卡方检验是一种用于检验两个或多个分类变量之间是否存在相关性的统计方法。卡方检验适用于分析分类数据，通常用于检验观测频数（frequency）与期望频数之间的差异是否显著。频数又称"次数"，是指变量值中代表某种特征的数（标志值）出现的次数。在R语言中，可以使用基本的chisq.test函数进行卡方检验。以下是关于卡方检验的详细介绍。

在单样本卡方检验中，我们测试一个分类变量的频数是否符合某种理论分布。假设检验的零假设是观测频数符合某种预期的分布。在R语言中，可以使用chisq.test函数指定观测频数和理论频数的期望比例，得出卡方统计量和p值。

在卡方检验中，关键的输出包括卡方统计量、自由度和p值。p值通常用来判断检验结果的显著性。如果p值小于显著性水平（通常为0.05），则可以拒绝零假设，认为观测频数与期望频数存在显著差异，或者两个分类变量之间存在相关性。

执行卡方检验的示例R代码如下：

复制代码

#创建数据框

data <- data.frame(

  PatientID = 1:80,

  Treatment = c(rep("TreatmentA", 40), rep("TreatmentB", 40)),

  CureStatus = c(rep("Cured", 30), rep("Cured", 30), rep("Not Cured", 20))

)

#创建列联表

table_data <- table(data$Treatment, data$CureStatus)

#进行卡方检验

chi_result <- chisq.test(table_data)

#输出结果

print(chi_result)

代码的运行结果如图5-3所示，该图展示了卡方检验的结果。通过chisq.test函数计算得出的卡方统计量的X-squared值为24.067、p值为9.306e-07。p值小于0.05，说明治疗方法和治愈结果之间存在显著关联。

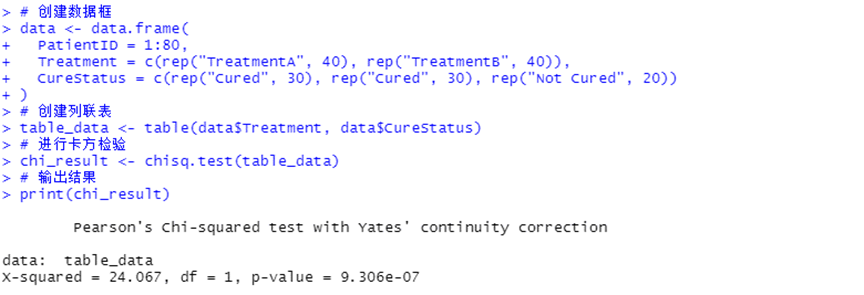
图5-3

总的来说，卡方检验是一种常用的统计方法，用于检验分类变量之间的相关性，能够帮助研究者在数据分析中进行合理的推断。在R语言中，使用chisq.test函数进行卡方检验非常方便，能够快速准确地进行相关性分析。

5.1.4 简单线性回归分析

简单线性回归分析是统计学中经常使用的一种方法，用于建立和评估一个自变量对一个连续因变量的线性关系。简单线性回归分析通过拟合一条直线来描述自变量与因变量之间的关系，以预测和解释因变量的变化。下面是关于简单线性回归分析的详细介绍：

简单线性回归模型可以表示为：

Y = β ~0~ +β ~1~X + ε

其中，Y 是因变量（响应变量）、X 是自变量、β ~0~是截距项、β ~1~是斜率、ε是误差项（随机误差）。

回归分析的目标是通过估计截距和斜率，拟合一条最优的直线来描述自变量和因变量之间的关系。通常使用最小二乘法来估计回归系数，使得预测值与实际值的残差平方和最小化。简单线性回归模型可以用来预测因变量的取值，也可以用来推断自变量和因变量之间的关系程度。

在R语言中，可以使用lm()函数进行简单线性回归分析。具体步骤包括：

收集自变量和因变量的数据。

运行lm()函数，指定因变量与自变量，得出回归系数、拟合直线及相关统计指标。

通过summary()函数获取回归模型的摘要统计信息，包括截距、斜率、R方值、t值和p值等。

简单线性回归分析能够帮助研究者理解和预测变量之间的关系，它提供了一种简单而有效的工具来解释和探究数据背后的模式和规律。执行简单线性回归分析的示例R代码如下：

复制代码

#创建数据框

data <- data.frame(

  Weight = c(61, 75, 83, 92, 100),  #体重，单位：千克

  BloodPressure = c(110, 123, 130, 150, 160)  #血压，单位：毫米汞柱

)

#进行简单线性回归分析

model <- lm(BloodPressure ~ Weight, data = data)

#查看模型输出结果

summary(model)

lm()函数中的"BloodPressure ~ Weight"表示正在拟合一个模型，其中血压（BloodPressure）是因变量，体重（Weight）是自变量，"data = data"指定了包含数据的数据框。Summary()函数将提供模型的详细摘要，包括回归系数、截距、R平方值、F统计量和p值等。这些统计量可以帮助我们了解模型的拟合情况和变量之间的线性关系是否显著。代码运行结果如图5-4所示，该图展示了简单线性回归的结果。

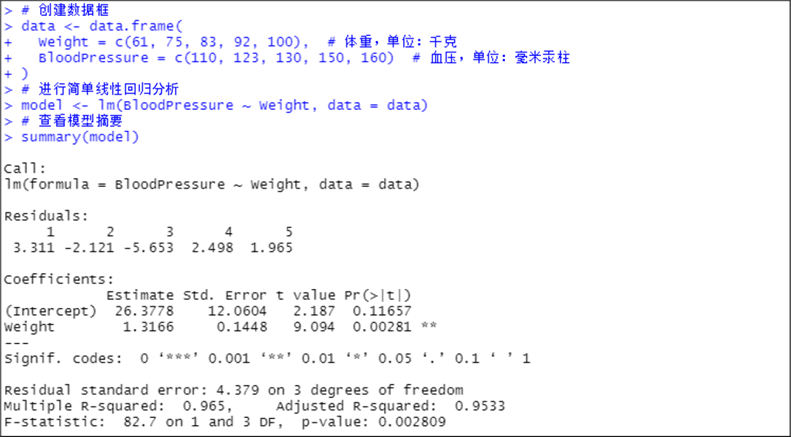
图5-4

从图5-4中可以看到，截距（Intercept）是26.3778，斜率（Weight的系数）是1.3166，这表示每增加1千克体重，血压平均增加1.3166毫米汞柱；p值为0.02809，小于0.05，表明体重与血压之间存在显著的线性关系；R平方值（Multiple R-squared）为0.965，表示模型解释了96.5%的血压变异。

复制代码

https://www.cnblogs.com/brucexia/p/18466799