AES

The Advanced Encryption Standard

On October 2, 2000, Rijndael was selected to be the Advanced Encryption Standard

Mathematical Preliminaries

Finite Fields

All byte values in AES will be presented as the concatenation of its individual bit values(0 or 1) in order : $\{a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0\}$

The bytess in AES are interpreted as finite field elements using a polynomial representation:

$\{a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0\} \\ \rightarrow a_7x^7+ a_6x^6+ a_5x^5 + a_4x^4 + a_3x^3 + a_2 x^2 + a_1x^1+a_0x^0 \\ = \sum_{i=0}^{i=7}b_ix^i$

Addition

The addition of two elements in a finite field is achieved by adding the coefficients for the corresponding powers in the polynomials for the two elements.

The addition is performed with the XOR operation:

For two bytes : $\{a_7, a_6, a_5, a_4, a_3, a_2, a_1, a_0\} , \{b_7, b_6, b_5, b_4, b_3, b_2, b_1, b_0\}$ , the sum is $\{c_7, c_6, c_5, c_4, c_3, c_2, c_1, c_0\}$ , where each $c_i = a_i \oplus b_i$

1 + 1 mod 2 = 0
1 + 0 mod 2 = 1
0 + 1 mod 2 = 1
0 + 0 mod 2 = 0

1 - 1 mod 2 = 0
1 - 0 mod 2 = 1
0 - 1 mod 2 = 1
0 - 0 mod 2 = 0

Subtraction of polynomials is identical to addition of polynomials.

Multiplication

In the polynomial representation, multiplication in $GF(2^8)$ (denoted by $\cdot$) corresponds with the multiplication of polynomials modulo an irreducible polynomial of degree 8

A polynomial is irreducible if its only divisors are one and itself. For AES, this irreducible polynomial is $m(x)=x^8+x^4+x^3+x+1$

For any non-zero binary polynomial $b(x)$ , the multiplicative inverse of $b(x)$ , denoted $b(x)^{-1}$ can be found as:

The extended Euclidean algorithm is used to compute polynomials $a(x)$ and $c(x)$ such that: $b(x)a(x)+ m(x)c(x) = 1$ .

Hence $b(x)^{-1} = a(x) mod \space m(x)$

Multiplication by x

$a(x)=a_7x^7+ a_6x^6+ a_5x^5 + a_4x^4 + a_3x^3 + a_2 x^2 + a_1x^1+a_0x^0$

$a(x)\cdot x \rightarrow a_7x^8+ a_6x^7+ a_5x^6 + a_4x^5 + a_3x^4 + a_2 x^3 + a_1x^2+a_0x^1$

$a(x)\cdot x$ is obtained by modulo $m(x)$
- $a_7=0$ : Done
- $a_7=1$ : $a(x)\cdot x $ modulo $m(x)$ i.e. XOR $m(x) = \{01\} \{1b\}$

$\Longrightarrow$ multiplication by x (i.e., {00000010} or {02}) can be implemented at the byte level as:

a left shift
a conditional bitwise XOR with {1b}

This operation on bytes is denoted by xtime() , Multiplication by higher power of x can be implemented by repeated application of xtime()

一定要注意数字是十进制还是十六进制还是二进制！！！！

$57\cdot 02 = xtime(57) =xtime(0101 \space 0111)= ae$

$\begin{align*}57 \cdot 04 &= xtime(ae) = xtime(1010\space 1110) \\&= 0101110 \space 0 \oplus 00011011 = 01000111 = 47_{16}\end{align*}$

$57\cdot 08 = xtime(01000111) = 10001110_2 = 8e_{16}$

$57\cdot 10_{16} = 00011100\oplus00011011 = 00000111 = 07_{16}$

$\begin{align*}57_{16}\cdot13_{16} &= 57_{16}\cdot (00010011)2\\ &= 57{16}\cdot(01_{16}\oplus02_{16}\oplus10_{16}) \\&=57\cdot 01 \oplus 57\cdot 02\oplus 57\cdot 10 \\&= 57 \oplus ae\oplus 07 \end{align*}$

Polynimials with Coefficients in GF( $2^8$)

**Four term polynomials can be defined with coefficients that are finite field elements : ** $a(x) = a_3x^3+a_2x^2+a_1x+a_0$ , which will be denoted as a word in the form $[a_0, a_1, a_2, a_3]$

!!!! The coefficients here are finite field elements themselves, i.e. bytes, instead of bits

Addition

Addition is performed by adding the finite field coefficients of like power of x . This addition corresponds to an XOR operation between the corresponding bytes in each of the words.

$a(x) + b(x) = (a_3\oplus b_3)x^3+(a_2\oplus b_2)x^2 + (a_1\oplus b_1)x + (a_0\oplus b_0)$

Multiplication

$c(x) = a(x)\cdot b(x)$ is algebraically expanded, and like powers are collected :

$c(x) = c_6x^6+c_5x^5+c_4x^4+c_3x^3+c_2x^2+c_1x^1+c_0$

$\begin{align*} c_0 &= a_0\oplus b_0 , &c_4 &= a_3\cdot b_1 \oplus a_2\cdot b_2 \oplus a_1\cdot b_3 \\c_1&= a_1\cdot b_0\oplus a_0 \cdot b_1 , \space &c_5 &= a_3 \cdot b_2 \oplus a_2\cdot b_3 \\ c_2 &= a_2\cdot b_0 \oplus a_1 \cdot b_1 \oplus a_0\cdot b_2, \space& c_6 &= a_3 \cdot b_3 \\ c_3 &=a_3\cdot b_0 \oplus a_2\cdot b_1 \oplus a_1\cdot b_2 \oplus a_0 \cdot b_3 \end{align*}$
reduce $c(x)$ to modulo a polynomial of degree 4

$x^i \space mod \space (x^4 + 1) = x^{i \space mod \space 4}$

$\Longrightarrow$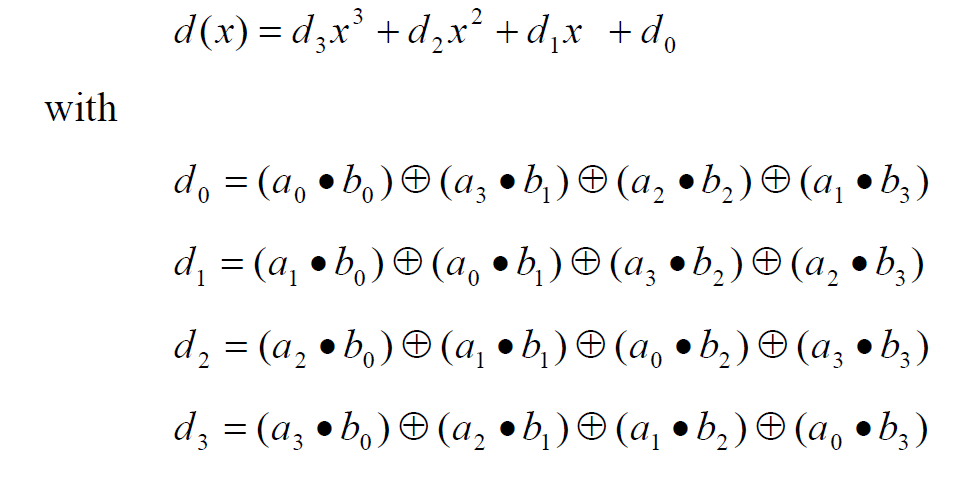

description

参数

Parameters & Functions

K : Cipher key
Nb : Number of columns (32-bit words) comprising the State. For AES, Nb = 4
Nk : Number of 32-bit words comprising the Cipher Key. For AES, Nk = 4, 6, 8
Nr : Number of rounds Nr = 10, 12, 14
Block length : 128

Block : Sequence of binary bits that comprise the input, output, State and Round Key. The length of a sequence is the number of bits it contains. Blocks are also interpreted as arrays of bytes.
Key length : 128, 192, 256 bits
$Nr$ : Nr = 10 if key length is 128 bits, Nr = 12 if key length is 192 bits, Nr = 14 if key length is 256 bits.

流程：

Initialize State to be plaintext x , then perform ADD-ROUNDKEY (x-ors the RoundKey with State)
For each of the first $Nr - 1$ rounds:
1. Perform a substitution operation : SUB-BYTES on State using a S-box.
2. Perform a permutation SHIF-TROWS on State
3. Perform a permutation MIX-COLUMNS on State
4. Perform ADD-ROUNDKEY
Perform SUB-TYPES, SHIFT-ROWS, ADD-ROUNDKEY
Define the ciphertext y to be State

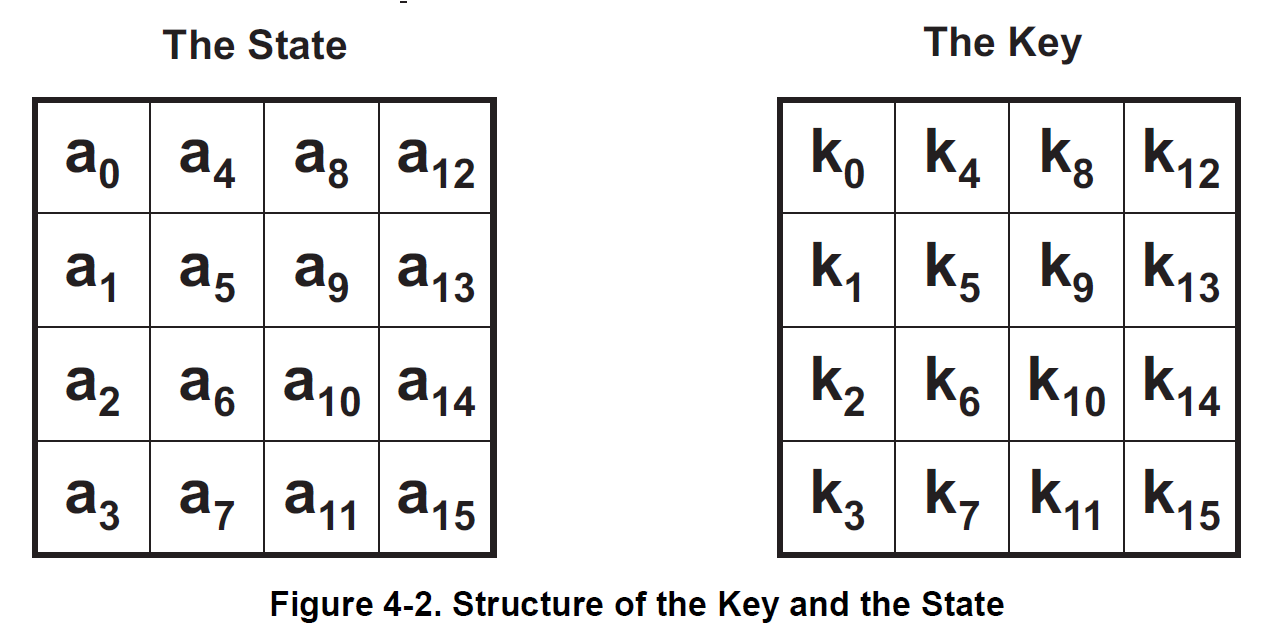
State(s 数组)

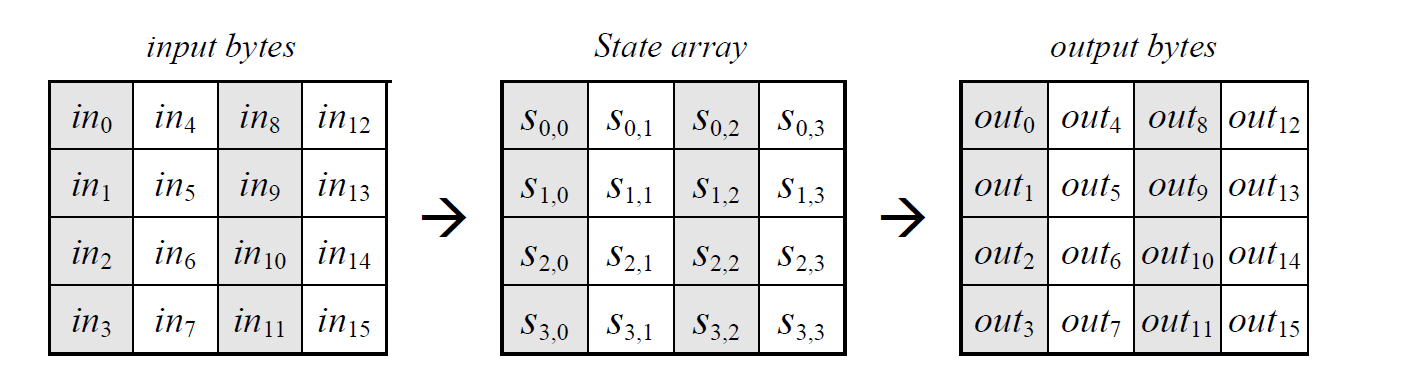
The State consists of four rows of bytes, each containing Nb bytes, where Nb is the block length divided by 32.

In the State array denoted by the symbol s , each individual byte has two indices(索引)， with its row number r : $0 \le r\le 4$, and its column number c : $0 \le c \le Nb$

Hence, at the beginning of the Cipher or Inverse Cipher, the input array, in , is copied to the State array according to the scheme:

$s[r][c] = in[r + 4c],$

$out[r+4c] = s[r][c] , for \space 0\le r\le3, 0 \le c \le Nb -1$

The four bytes in each column of the State array form 32-bit words, where the row number r provides an index for the four bytes within each word. The state can hence be interpreted as a one-dimensional array of 32 bit words: $w_0, w_1, w_2, w_3$

$w_0 = s_{0, 0}, s_{1, 0}, s_{2, 0}, s_{3, 0}$

$w_1 = s_{0, 1}, s_{1, 1}, s_{2, 1}, s_{3, 1}$

$w_2 = s_{0, 2}, s_{1, 2}, s_{2, 2}, s_{3, 2}$

$w_3 = s_{0, 3}, s_{1, 3}, s_{2, 3}, s_{3, 3}$

Key Expansion

The Key Expansion generates a total of $Nb(Nr+1)$ words( Require an initial set of Nb words).

The resulting key schedule consists of a linear array of 4-byte words, denoted $[w_i]$ , with $i$ in range $0 \le i \le Nb(Nr+1)$

KeyExpansion(byte key[4*Nk], word x[Nb*(Nr+1)], Nk)
begin 
	word temp
	i = 0
	
	while(i < Nk)
		w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3])
		i = i+1
	end while
	
	while(i < Nb * (Nr + 1))
		temp = w[i-1]
		if (i mod Nk == 0)
			temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]
		else if (Nk > 6 and i mod Nk = 4)
			temp = SubWord(temp)
		end if
		w[i] = w[i-Nk] xor temp
		i = i + 1
	end while
end

The first Nk words of the expanded key are filled with the Cipher Key
Following word : w[i]
- If : $i \equiv 0 \mod Nk$ , $SubWord(RotWord(w[i-1])) \oplus Rcon[i/Nk]$
- else : $w[i] = w[i-1] \oplus w[i-Nk]$

ROTWORD

$ROTWORD(B_0, B_1, B_2, B_3)$ , performs a cyclic shift of the four bytes : $ROTWORD(B_0, B_1, B_2, B_3) = (B_1, B_2, B_3, B_0)$

SUBWORD

Apply the S-box to each of the four bytes : $SUBWORD(B_0, B_1, B_2, B_3) =(B_0^{'}, B_1^{'}, B_2^{'}, B_3^{'})$

where $B_i^{'} = SUBBYTES(B_i)$

RCon

an array of 10 words. Constants given by $[x^{i-1}, 00, 00, 00]$ , ($x^{i-1}$ is the powers of x , x is denoted as {02} in the field $GF(2^8)$)

$RCon[1] \leftarrow 01000000$

$RCon[2] \leftarrow 02000000$

$RCon[3] \leftarrow 04000000$

$RCon[4] \leftarrow 08000000$

$RCon[5] \leftarrow 10000000$

$RCon[6] \leftarrow 20000000$

$RCon[7] \leftarrow 40000000$

$RCon[8] \leftarrow 80000000$

$RCon[9] \leftarrow1B000000$

$RCon[10] \leftarrow 36000000$

代码实现

c 复制代码

u8** KeyExpansion(u8* k) {

    // Round Constant
    u8** RCon = CalRoundConstant();
    u8** w = (u8**)malloc(sizeof(u8*) * Nb * (Nr + 1));
    for(int i = 0; i < 4; i++) {
        w[i] = (u8*)malloc(sizeof(u8) * 4);
    }

    int i = 0;
    u8* tmp;

    // w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3]), i < Nk
    for(; i < Nk; i++) {
        for(int j = 0; j < 4; j++) {
            w[i][j] = k[i + 4 * j];
        }
    }

    while(i < Nb * (Nr + 1)) {
        tmp = Byte2Word(w, i - 1);
        if(!(i % Nk)) {
            // temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]
            RotWord(tmp);
            SubWord(tmp);
            for(int j = 0; j < 4; j++) {
                tmp[j] = GFAdd(tmp[j], RCon[j][i/Nk]) ;
            }
        } else if ((Nk > 6) && (i % Nk == 4)){
            SubWord(tmp);
        }

        // w[i] = w[i-Nk] xor temp
        for(int j = 0; j < 4 ; j++) {
            w[j][i] = w[j][i - Nk] ^ tmp[j];
        }
        i++;
    }
    return w;
}

cipher

流程分析

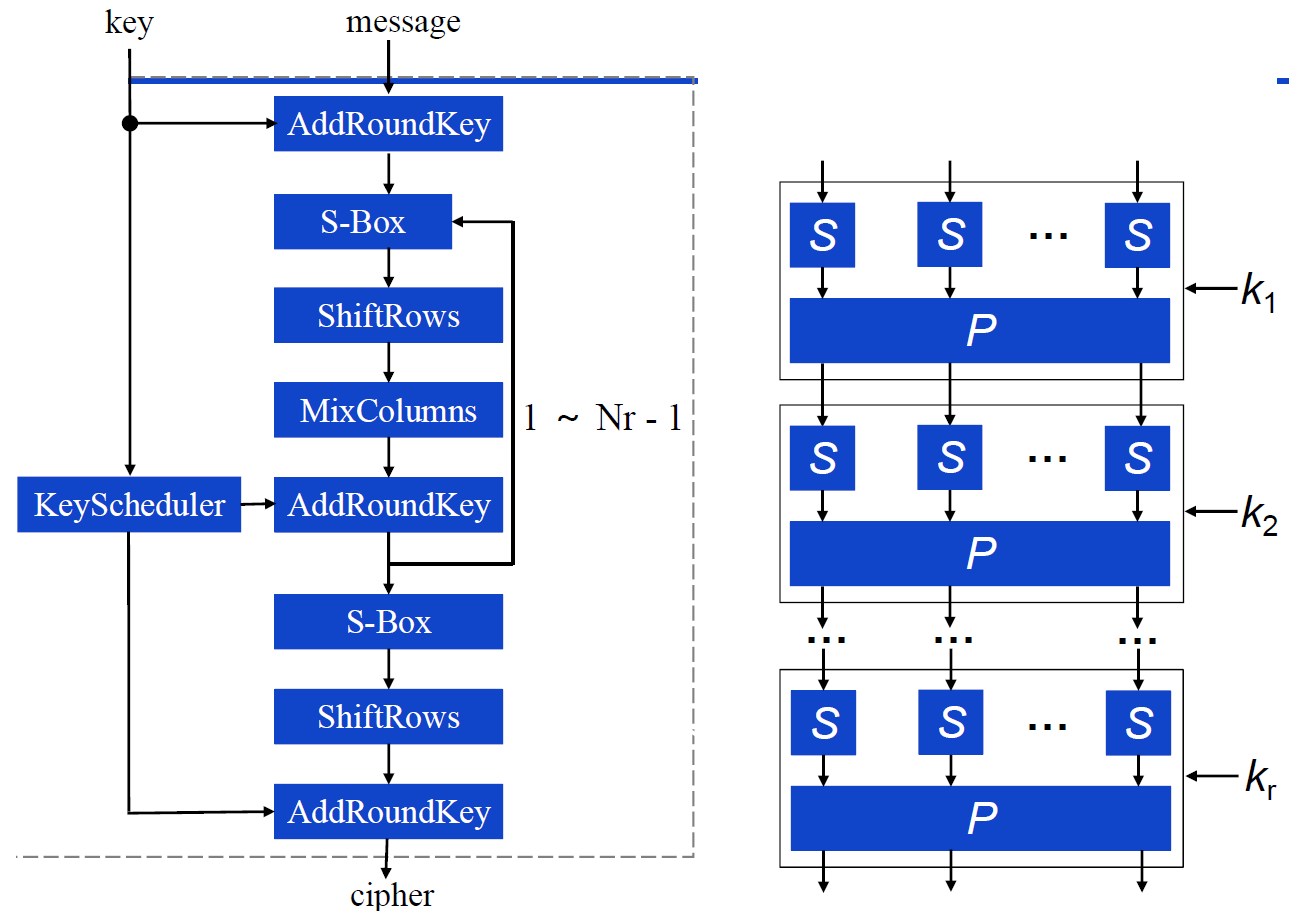
Cipher(byte in[4*Nb], type out[4*Nb], word w[Nb*(Nr + 1)]) // w[] contains the key schedule
begin
	byte state[4][Nb]
	
	state = in
	
	AddRoundKey(state, w[0, Nb - 1])
	
	for round = 1 step 1 to Nr - 1
        SubBytes(state) // substitute bytes
        ShiftRows(state)
        MixColumns(state)
        AddRoundKey(state, w[round*Nb, (round+1)*Nb - 1])
	end for
	
	SubBytes(state)
	ShiftRows(state)
	AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
	
	out = state
end

`SubBytes`

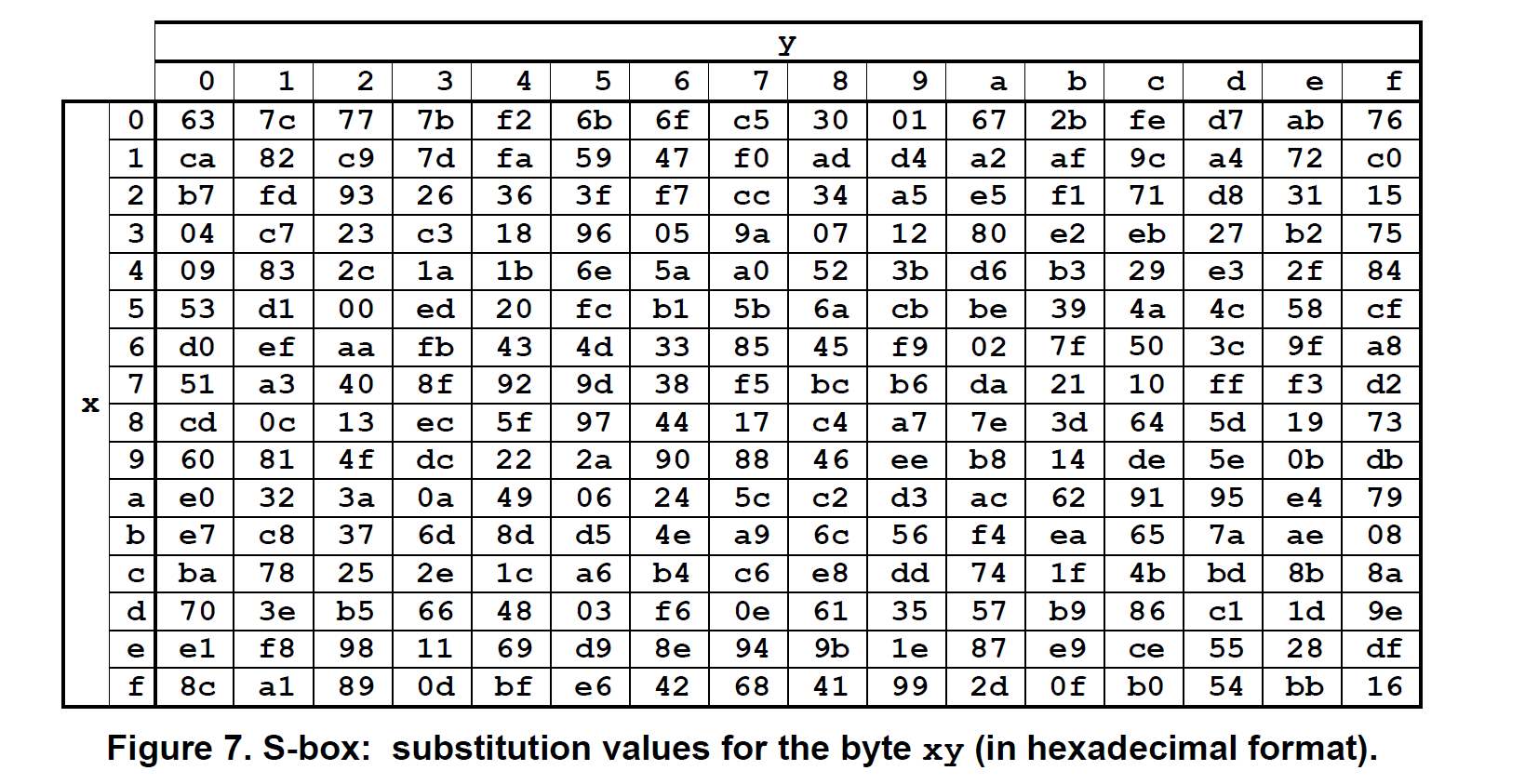
Non-linear byte substitution that operates independently on each byte of the State using a substitution table(S-box ) , which is a permutation of $\{0, 1\}^8$

In contrast to the S-boxes in DES, which are apparently "random" substitutions, the AES S-box can be defined algebraically.

$\pi_S$操作:

the permutation $\pi_S$ incorporates operations in the finite field : $F_{2^8} = Z_2[x]/(x^8+x^4+x^3+x+1)$ (主要是求逆元操作 : $a(x)b(x)\equiv 1\mod m(x)$)

Take the multiplicative inverse in the finite field $GF(2^8)$( 把字节看做有限域 $2^8$ 上的元素)
Affine transformation(over $GF(2)$): $b_i^{'} = b_i\oplus b_{(i+ 4) mod \space 8} \oplus b_{(i+ 5) mod \space 8} \oplus b_{(i+ 6) mod \space 8} \oplus b_{(i+ 7) mod \space 8} \oplus c_i$

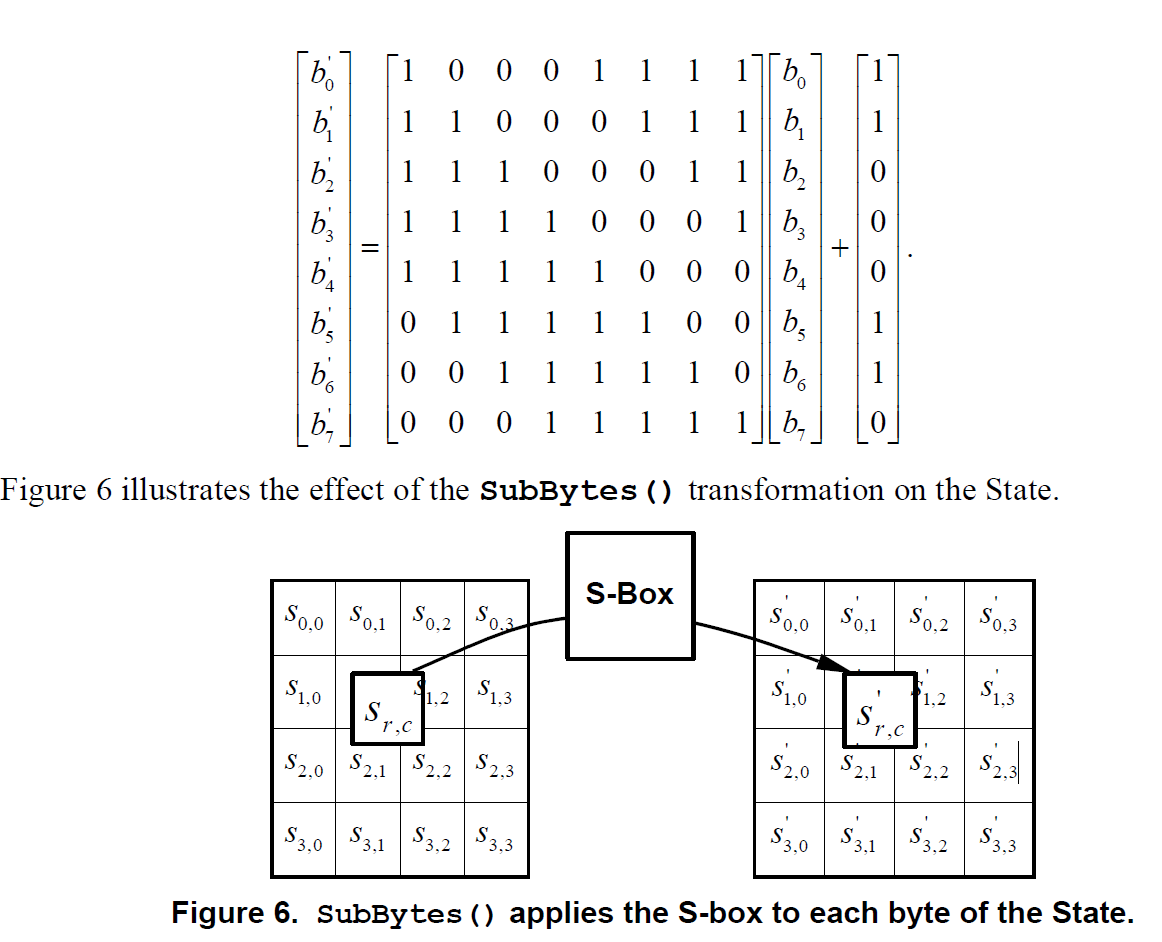
伪代码：

SUBTYPES ($a_7a_6a_5a_4a_3 a_2 a_1 a_0$)

external FIELDINV, BINARYTOFIELD, FIELDTOBINARY

$z \leftarrow BINARYTOFIELD(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0)$

if $z \ne 0$

then $z\leftarrow FIELDINV(z)$

$(a_7 a_6 a_5 a_4 a_3 a_2 a_1 a_0) \leftarrow FIELDTOBINARY(z)$

$(c_7 c_6 c_5 c_4 c_3 c_2 c_1 c_0)\leftarrow(01100011) $

/// All subscripts are to be reduced modulo 8 in the following loop

for $i \leftarrow 0 \space to \space 7$ :

DO $b_i \leftarrow (a_i +a_{i+4} +a_{i + 5} +a_{i + 7} +c_i) \space mod \space 2$

return $(b_7 b_6 b_5 b_4 b_3 b_2 b_1 b_0)$

由于对每个已知输入，经过 S 盒的输出都是固定的，可以直接将 S 盒写成替代表的形式来减少计算开销。

代码实现

c 复制代码

void SubBytes(u8** a) {
    for(int j = 0; j < Nb; j++) {
        for(int i = 0; i < 4; i++) {
            a[i][j] = s_box[a[i][j] >> 4][a[i][j] & 0x0f];
        }
    }
}

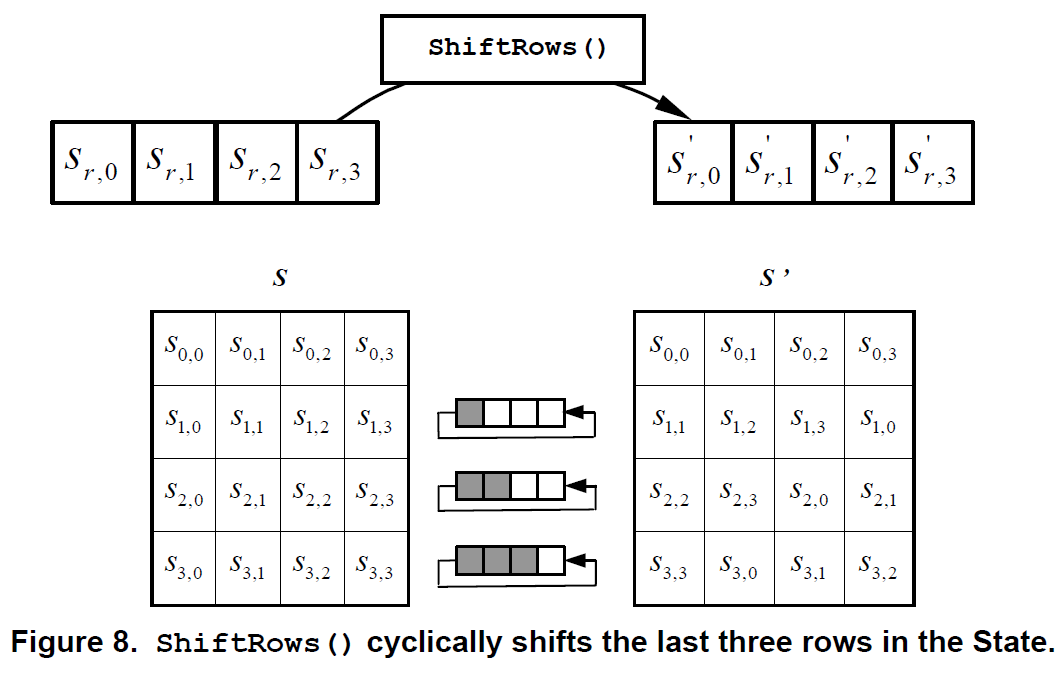
`ShiftRows()`

$S^{'}{r, c} = S{r, (c+shift(r, Nb)) \space mod \space Nb}, \space 0 \lt r \lt4 \space and \space 0 \le c \lt Nb$

$shift(1, 4) = 1; shift(2, 4)=2.; shift(3,4)=3$

代码实现

c 复制代码

void ShiftRows(u8** a) {
    u8* tmp = (u8*)malloc(sizeof(u8)* Nb);

    for(int i = 1; i < 4; i++) {
        for(int j = 0; j < Nb; j++) {
            tmp[j] = a[i][j];
        }
        for(int j = 0; j < Nb; j++) {
            a[i][j] = tmp[(j + i) % Nb];
        }
    }

    free(tmp);
}

`MixColumns()`

MixColumns operates in the State column-by-column, treating each column as a four-term polynomial over $GF(2^8)$ and multiplied modulo $x^4+1$ with a fixed polynomial $a(x) = \{03\}x^3 + \{01\}x^2 + \{01\}x+ \{02\}$

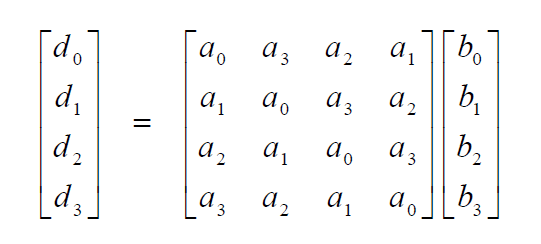
$\Longrightarrow $

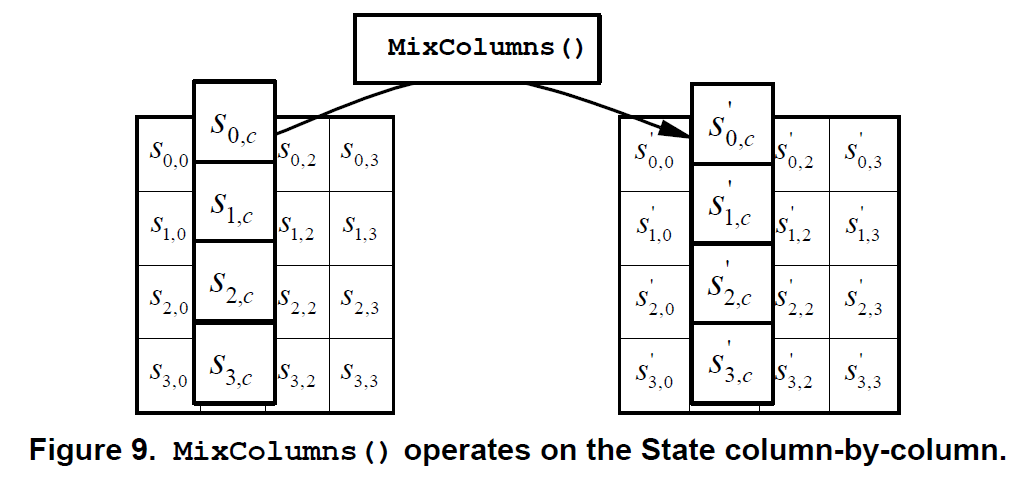
乘法操作可以通过 x 乘实现

代码实现：

c 复制代码

void MixColumns(u8** a) {
    u8 tmp[4];
    for(int j = 0; j < Nb; j++) {
        tmp[0] = a[0][j];
        tmp[1] = a[1][j];
        tmp[2] = a[2][j];
        tmp[3] = a[3][j];
        a[0][j] = xtime(tmp[0]) ^ xtime(tmp[1]) ^ tmp[1] ^ tmp[2] ^ tmp[3];
        a[1][j] = tmp[0] ^ xtime(tmp[1]) ^ xtime(tmp[2]) ^ tmp[2] ^ tmp[3];
        a[2][j] = tmp[0] ^ tmp[1] ^ xtime(tmp[2]) ^ xtime(tmp[3]) ^ tmp[3];
        a[3][j] = xtime(tmp[0]) ^ tmp[0] ^ tmp[1] ^ tmp[2] ^ xtime(tmp[3]);
    }
}

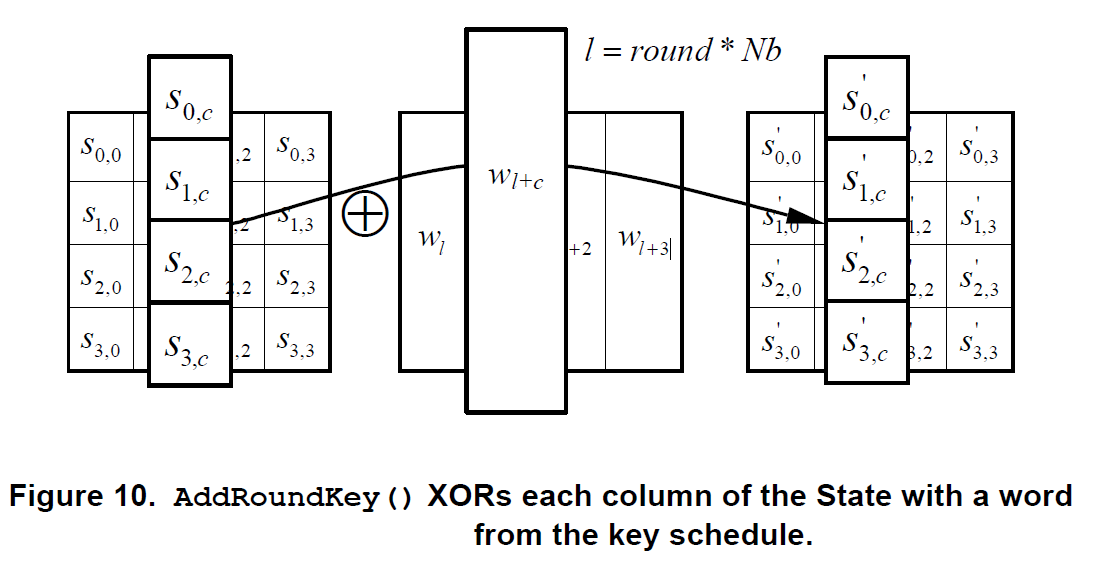
`AddRoundKey()`

$[s_{0, c}^{'}, s_{1, c}^{'}, s_{2, c}^{'}, s_{3, c}^{'}] = [s_{0, c}, s_{1, c}, s_{2, c}, s_{3, c}] \oplus [w_{round*Nb ,c}]$

代码实现

c 复制代码

u8* AddRoundKey(u8** state, u8** w, int round) {
    for(int j = 0; j < Nb; j++){
        for(int i = 0; i < 4; i++) {
            state[i][j] = GFAdd(state[i][j], w[i][round * 4 + j]) ;
        }
    }
}

解密

直接反向解密

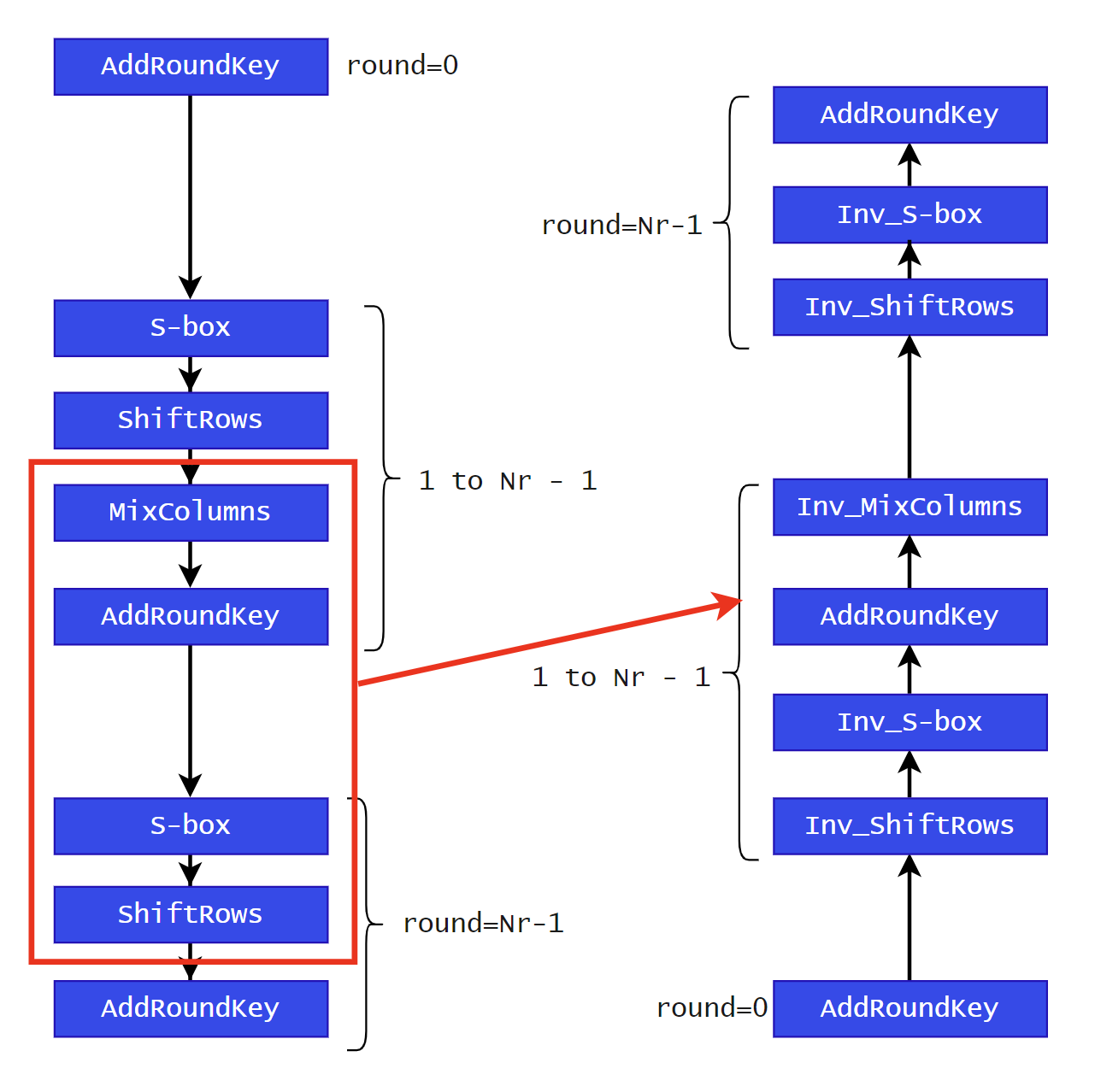
Inv_ShiftRows: 反向右移
Inv_S-box : S 先逆仿射变换再求逆
Inv_MixColumns : 乘以矩阵的乘法逆元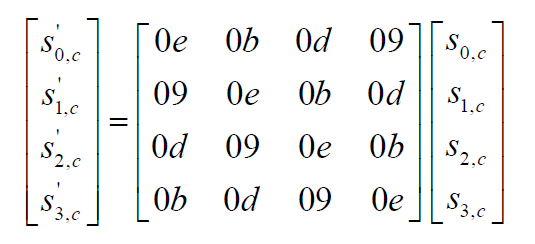
AddRoundKey : 逆变换即为自身

Pseudo Code

InvCipher(byte in[4*Nb], byte out[4*Nb], word w[Nb*(Nr+1)])
begin
	byte state[4,Nb]
	
	state = in
	
	AddRoundKey(state, w[Nr*Nb, (Nr+1)*Nb-1])
	
	for round = Nr-1 setp -1 to 1
		InvShiftRows(state)
		InvSubBytes(state)
		AddRoundKey(state, w[round*Nb, (round+1)*Nb-1])
		InvMixColumns(state)
	end for
	
	InvShiftRows(state)
	InvSubBytes(state)
	AddRoundKey(state, w[0, Nb-1])
	
	out = state
end

完整代码：

c 复制代码

#include<stdio.h>
#include<stdlib.h>
#include<stdint.h>
#include<string.h>
#define u8 uint8_t
#define u32 uint32_t

const int Nb = 4; // 分组字块数
int Nr;
int Nk;

static u8 s_box[16][16] = {
	// 0     1     2     3     4     5     6     7     8     9     a     b     c     d     e     f
	{0x63, 0x7c, 0x77, 0x7b, 0xf2, 0x6b, 0x6f, 0xc5, 0x30, 0x01, 0x67, 0x2b, 0xfe, 0xd7, 0xab, 0x76}, // 0
	{0xca, 0x82, 0xc9, 0x7d, 0xfa, 0x59, 0x47, 0xf0, 0xad, 0xd4, 0xa2, 0xaf, 0x9c, 0xa4, 0x72, 0xc0}, // 1
	{0xb7, 0xfd, 0x93, 0x26, 0x36, 0x3f, 0xf7, 0xcc, 0x34, 0xa5, 0xe5, 0xf1, 0x71, 0xd8, 0x31, 0x15}, // 2
	{0x04, 0xc7, 0x23, 0xc3, 0x18, 0x96, 0x05, 0x9a, 0x07, 0x12, 0x80, 0xe2, 0xeb, 0x27, 0xb2, 0x75}, // 3
	{0x09, 0x83, 0x2c, 0x1a, 0x1b, 0x6e, 0x5a, 0xa0, 0x52, 0x3b, 0xd6, 0xb3, 0x29, 0xe3, 0x2f, 0x84}, // 4
	{0x53, 0xd1, 0x00, 0xed, 0x20, 0xfc, 0xb1, 0x5b, 0x6a, 0xcb, 0xbe, 0x39, 0x4a, 0x4c, 0x58, 0xcf}, // 5
	{0xd0, 0xef, 0xaa, 0xfb, 0x43, 0x4d, 0x33, 0x85, 0x45, 0xf9, 0x02, 0x7f, 0x50, 0x3c, 0x9f, 0xa8}, // 6
	{0x51, 0xa3, 0x40, 0x8f, 0x92, 0x9d, 0x38, 0xf5, 0xbc, 0xb6, 0xda, 0x21, 0x10, 0xff, 0xf3, 0xd2}, // 7
	{0xcd, 0x0c, 0x13, 0xec, 0x5f, 0x97, 0x44, 0x17, 0xc4, 0xa7, 0x7e, 0x3d, 0x64, 0x5d, 0x19, 0x73}, // 8
	{0x60, 0x81, 0x4f, 0xdc, 0x22, 0x2a, 0x90, 0x88, 0x46, 0xee, 0xb8, 0x14, 0xde, 0x5e, 0x0b, 0xdb}, // 9
	{0xe0, 0x32, 0x3a, 0x0a, 0x49, 0x06, 0x24, 0x5c, 0xc2, 0xd3, 0xac, 0x62, 0x91, 0x95, 0xe4, 0x79}, // a
	{0xe7, 0xc8, 0x37, 0x6d, 0x8d, 0xd5, 0x4e, 0xa9, 0x6c, 0x56, 0xf4, 0xea, 0x65, 0x7a, 0xae, 0x08}, // b
	{0xba, 0x78, 0x25, 0x2e, 0x1c, 0xa6, 0xb4, 0xc6, 0xe8, 0xdd, 0x74, 0x1f, 0x4b, 0xbd, 0x8b, 0x8a}, // c
	{0x70, 0x3e, 0xb5, 0x66, 0x48, 0x03, 0xf6, 0x0e, 0x61, 0x35, 0x57, 0xb9, 0x86, 0xc1, 0x1d, 0x9e}, // d
	{0xe1, 0xf8, 0x98, 0x11, 0x69, 0xd9, 0x8e, 0x94, 0x9b, 0x1e, 0x87, 0xe9, 0xce, 0x55, 0x28, 0xdf}, // e
	{0x8c, 0xa1, 0x89, 0x0d, 0xbf, 0xe6, 0x42, 0x68, 0x41, 0x99, 0x2d, 0x0f, 0xb0, 0x54, 0xbb, 0x16}};// f

static u8 inv_s_box[16][16] = {
	// 0     1     2     3     4     5     6     7     8     9     a     b     c     d     e     f
	{0x52, 0x09, 0x6a, 0xd5, 0x30, 0x36, 0xa5, 0x38, 0xbf, 0x40, 0xa3, 0x9e, 0x81, 0xf3, 0xd7, 0xfb},	 // 0
	{0x7c, 0xe3, 0x39, 0x82, 0x9b, 0x2f, 0xff, 0x87, 0x34, 0x8e, 0x43, 0x44, 0xc4, 0xde, 0xe9, 0xcb},	 // 1
	{0x54, 0x7b, 0x94, 0x32, 0xa6, 0xc2, 0x23, 0x3d, 0xee, 0x4c, 0x95, 0x0b, 0x42, 0xfa, 0xc3, 0x4e},	 // 2
	{0x08, 0x2e, 0xa1, 0x66, 0x28, 0xd9, 0x24, 0xb2, 0x76, 0x5b, 0xa2, 0x49, 0x6d, 0x8b, 0xd1, 0x25},	 // 3
	{0x72, 0xf8, 0xf6, 0x64, 0x86, 0x68, 0x98, 0x16, 0xd4, 0xa4, 0x5c, 0xcc, 0x5d, 0x65, 0xb6, 0x92},	 // 4
	{0x6c, 0x70, 0x48, 0x50, 0xfd, 0xed, 0xb9, 0xda, 0x5e, 0x15, 0x46, 0x57, 0xa7, 0x8d, 0x9d, 0x84},	 // 5
	{0x90, 0xd8, 0xab, 0x00, 0x8c, 0xbc, 0xd3, 0x0a, 0xf7, 0xe4, 0x58, 0x05, 0xb8, 0xb3, 0x45, 0x06},	 // 6
	{0xd0, 0x2c, 0x1e, 0x8f, 0xca, 0x3f, 0x0f, 0x02, 0xc1, 0xaf, 0xbd, 0x03, 0x01, 0x13, 0x8a, 0x6b},	 // 7
	{0x3a, 0x91, 0x11, 0x41, 0x4f, 0x67, 0xdc, 0xea, 0x97, 0xf2, 0xcf, 0xce, 0xf0, 0xb4, 0xe6, 0x73},	 // 8
	{0x96, 0xac, 0x74, 0x22, 0xe7, 0xad, 0x35, 0x85, 0xe2, 0xf9, 0x37, 0xe8, 0x1c, 0x75, 0xdf, 0x6e},	 // 9
	{0x47, 0xf1, 0x1a, 0x71, 0x1d, 0x29, 0xc5, 0x89, 0x6f, 0xb7, 0x62, 0x0e, 0xaa, 0x18, 0xbe, 0x1b},	 // a
	{0xfc, 0x56, 0x3e, 0x4b, 0xc6, 0xd2, 0x79, 0x20, 0x9a, 0xdb, 0xc0, 0xfe, 0x78, 0xcd, 0x5a, 0xf4},	 // b
	{0x1f, 0xdd, 0xa8, 0x33, 0x88, 0x07, 0xc7, 0x31, 0xb1, 0x12, 0x10, 0x59, 0x27, 0x80, 0xec, 0x5f},	 // c
	{0x60, 0x51, 0x7f, 0xa9, 0x19, 0xb5, 0x4a, 0x0d, 0x2d, 0xe5, 0x7a, 0x9f, 0x93, 0xc9, 0x9c, 0xef},	 // d
	{0xa0, 0xe0, 0x3b, 0x4d, 0xae, 0x2a, 0xf5, 0xb0, 0xc8, 0xeb, 0xbb, 0x3c, 0x83, 0x53, 0x99, 0x61},	 // e
	{0x17, 0x2b, 0x04, 0x7e, 0xba, 0x77, 0xd6, 0x26, 0xe1, 0x69, 0x14, 0x63, 0x55, 0x21, 0x0c, 0x7d}}; // f

u8 GFAdd(u8 a, u8 b) {
    return a ^ b;
}

u8 GFSub(u8 a, u8 b) {
    return a ^ b;
}

u8 xtime(u8 a) {
    u8 msb = a & 0x80;
    a = a << 1;
    if(msb) {   
        return GFSub(a, 0x1b);
    } else {
        return a;
    }
} 

u8 GFMul(u8 a, u8 b) {
    u8 ans = 0;

    while(b) {
        if(b & 0x1) {
            ans = GFAdd(ans, a);
        }
        a = xtime(a);
        b = b >> 1;
    }
    return ans;
}


void RotWord(u8* a) {
    u8 tmp = a[0];
    a[0] = a[1];
    a[1] = a[2];
    a[2] = a[3];
    a[3] = tmp;
}

u8* Byte2Word(u8**a, int i) {
    u8* b = (u8*)malloc(sizeof(u8) * 4);
    b[0] = a[0][i];
    b[1] = a[1][i];
    b[2] = a[2][i];
    b[3] = a[3][i];
    return b;
}

void test_array(const char* str, u8** arr, int size) {
    printf("%s: ", str);
    for(int j = 0; j < size; j++) {
        for(int i = 0; i < 4; i++) {
            printf("%02x", arr[i][j]);
        }
        printf(" ");
    }
    printf("\n");
}



u8** CalRoundConstant() {
    u8** RCon = (u8**)malloc(sizeof(u8*)* 11);
    for(int i = 0; i < 11; i++) {
        RCon[i] = (u8*)malloc(sizeof(u8)*4);
    }
    for(int i = 1; i < 4; i++) {
        for(int j = 0; j < 11; j++) {
            RCon[i][j] = 0;
        }
    }
    RCon[0][1] = 0x01; 

    for(int i = 2; i <= 10; i++) {
        RCon[0][i] = xtime(RCon[0][i - 1]);
    }
    // test_array("RCon", RCon, 11);
    return RCon;
}

void ShiftRows(u8** a) {
    u8* tmp = (u8*)malloc(sizeof(u8)* Nb);

    for(int i = 1; i < 4; i++) {
        for(int j = 0; j < Nb; j++) {
            tmp[j] = a[i][j];
        }
        for(int j = 0; j < Nb; j++) {
            a[i][j] = tmp[(j + i) % Nb];
        }
    }

    free(tmp);
}

void InvShiftRows(u8** a) {
    u8* tmp = (u8*)malloc(sizeof(u8)* Nb);

    for(int i = 1; i < 4; i++) {
        for(int j = 0; j < Nb; j++) {
            tmp[j] = a[i][j];
        }
        for(int j = 0; j < Nb; j++) {
            a[i][j] = tmp[(j - i + Nb) % Nb];
        }
    }

    free(tmp);
}


void MixColumns(u8** a) {
    u8 tmp[4];
    for(int j = 0; j < Nb; j++) {
        tmp[0] = a[0][j];
        tmp[1] = a[1][j];
        tmp[2] = a[2][j];
        tmp[3] = a[3][j];
        a[0][j] = GFMul(tmp[0], 0x02) ^ GFMul(tmp[1], 0x03) ^ GFMul(tmp[2], 0x01) ^GFMul(tmp[3], 0x01);
        a[1][j] = GFMul(tmp[0], 0x01) ^ GFMul(tmp[1], 0x02) ^ GFMul(tmp[2], 0x03) ^GFMul(tmp[3], 0x01);
        a[2][j] = GFMul(tmp[0], 0x01) ^ GFMul(tmp[1], 0x01) ^ GFMul(tmp[2], 0x02) ^GFMul(tmp[3], 0x03);
        a[3][j] = GFMul(tmp[0], 0x03) ^ GFMul(tmp[1], 0x01) ^ GFMul(tmp[2], 0x01) ^GFMul(tmp[3], 0x02);
    }
}

void InvMixColumns(u8** a) {
    u8 tmp[4];
    for(int j = 0; j < Nb; j++) {
        tmp[0] = a[0][j];
        tmp[1] = a[1][j];
        tmp[2] = a[2][j];
        tmp[3] = a[3][j];
        a[0][j] = GFMul(tmp[0], 0x0e) ^ GFMul(tmp[1], 0x0b) ^ GFMul(tmp[2], 0x0d) ^GFMul(tmp[3], 0x09);
        a[1][j] = GFMul(tmp[0], 0x09) ^ GFMul(tmp[1], 0x0e) ^ GFMul(tmp[2], 0x0b) ^GFMul(tmp[3], 0x0d);
        a[2][j] = GFMul(tmp[0], 0x0d) ^ GFMul(tmp[1], 0x09) ^ GFMul(tmp[2], 0x0e) ^GFMul(tmp[3], 0x0b);
        a[3][j] = GFMul(tmp[0], 0x0b) ^ GFMul(tmp[1], 0x0d) ^ GFMul(tmp[2], 0x09) ^GFMul(tmp[3], 0x0e);
    }
}

u8* AddRoundKey(u8** state, u8** w, int round) {
    for(int j = 0; j < Nb; j++){
        for(int i = 0; i < 4; i++) {
            state[i][j] = GFAdd(state[i][j], w[i][round * 4 + j]) ;
        }
    }
}



void SubBytes(u8** a) {
    for(int j = 0; j < Nb; j++) {
        for(int i = 0; i < 4; i++) {
            a[i][j] = s_box[a[i][j] >> 4][a[i][j] & 0x0f];
        }
    }
}

void InvSubBytes(u8** a) {
    for(int j = 0; j < Nb; j++) {
        for(int i = 0; i < 4; i++) {
            a[i][j] = inv_s_box[a[i][j] >> 4][a[i][j] & 0x0f];
        }
    }
}


void SubWord(u8* a) {
    for(int i = 0; i < 4; i++) {
        a[i] = s_box[a[i] >> 4][a[i] & 0x0f];
    }
}




u8** KeyExpansion(u8* k) {

    // Round Constant
    u8** RCon = CalRoundConstant();
    u8** w = (u8**)malloc(sizeof(u8*) * Nb * (Nr + 1));
    for(int i = 0; i < 4; i++) {
        w[i] = (u8*)malloc(sizeof(u8) * 4);
    }

    int j = 0;
    u8* tmp;

    // w[i] = word(key[4*i], key[4*i+1], key[4*i+2], key[4*i+3]), i < Nk
    for(; j < Nk; j++) {
        for(int i = 0; i < 4; i++) {
            w[i][j] = k[i + 4 * j];
        }
    }

    while(j < Nb * (Nr + 1)) {
        tmp = Byte2Word(w, j - 1);
        if(!(j % Nk)) {
            // temp = SubWord(RotWord(temp)) xor Rcon[i/Nk]
            RotWord(tmp);
            SubWord(tmp);
            for(int i = 0; i < 4; i++) {
                tmp[i] = GFAdd(tmp[i], RCon[i][j/Nk]) ;
            }
        } else if ((Nk > 6) && (j % Nk == 4)){
            SubWord(tmp);
        }

        // w[i] = w[i-Nk] xor temp
        for(int i = 0; i < 4 ; i++) {
            w[i][j] = w[i][j - Nk] ^ tmp[i];
        }
        j++;
    }
    return w;
}


u8** init(int key_size, u8* k, u8** state, u8* in) {
    switch (key_size) { // 128/192/256bits
        case 16: Nk = 4; Nr = 10; break;
        case 24: Nk = 6; Nr = 12; break;
        case 32: Nk = 8; Nr = 14; break;
    }
    u8** w = KeyExpansion(k);

    for(int j = 0; j < Nb; j++) {
        for(int i = 0; i < 4; i++) {
            state[i][j] = in[i + 4 * j];
        }
    }
    return w;
}

void AesEncrypt(int key_size, u8* k, u8* in, u8*out) {

    u8** state = (u8**)malloc(sizeof(u8*) * Nb);
    for(int i = 0; i < 4; i++) {
        state[i] = (u8*)malloc(sizeof(u8) * 4);
    }

    u8** w = init(key_size, k, state, in);
    
    AddRoundKey(state, w, 0);
    for(int round = 1; round < Nr; round++) {
        SubBytes(state); 
        ShiftRows(state); 
        MixColumns(state); 
        AddRoundKey(state, w, round); 
    }

    // last round
    SubBytes(state);
    ShiftRows(state);
    AddRoundKey(state, w, Nr);

    for(int j = 0; j < Nb; j++) {
        for(int i = 0; i < 4; i++) {
            out[i + 4 * j] = state[i][j];
        }
    }
    free(w);
    free(state);
}





u8* AesDecrypt(int key_size, u8* k, u8* in, u8*out) {
    /*in: encrypt_text, out : decrypt_text*/

    u8** state = (u8**)malloc(sizeof(u8*) * Nb);
    for(int i = 0; i < 4; i++) {
        state[i] = (u8*)malloc(sizeof(u8) * 4);
    }
    u8** w = init(key_size, k, state, in); // w stores the expanded key
    AddRoundKey(state, w, Nr);
    for(int round = Nr - 1; round > 0; round--) {
        InvShiftRows(state);
        InvSubBytes(state);
        AddRoundKey(state, w, round);
        InvMixColumns(state);
    }

    InvShiftRows(state);
    InvSubBytes(state);
    AddRoundKey(state, w, 0);

    for(int j = 0; j < Nb; j++) {
        for(int i = 0; i < 4; i++) {
            out[i + 4 * j] = state[i][j];
        }
    }
    free(w);
    free(state);
}

void display(u8* a) {
    for(int i = 0; i < Nb * 4; i++)
    printf("%02x", a[i]);
    printf("\n");
}

int main() {
    u8* encrypt_text = (u8*)malloc(sizeof(u8) * (4 * Nb));
    u8* decrypt_text = (u8*)malloc(sizeof(u8) * (4 * Nb));
    unsigned char plain_text[16] = "zzzzyyyyxxxxwwww";

    unsigned char key_16[16] = "abcdefghijklmnop";
    unsigned char key_24[24] = "abcdefghijklmnopqrstuvwx";
    unsigned char key_32[32] = "abcdefghijklmnopqrstuvwxyyyyzzzz";

    // keysize = 128 bits
    AesEncrypt(16, key_16, plain_text, encrypt_text);
    display(encrypt_text);

    AesDecrypt(16, key_16, encrypt_text, decrypt_text);
    display(decrypt_text);


    // keysize = 192 bits
    AesEncrypt(24, key_24, plain_text, encrypt_text);
    display(encrypt_text);

    AesDecrypt(24, key_24, encrypt_text, decrypt_text);
    display(decrypt_text);

    //keysize = 256 bits
    AesEncrypt(32, key_32, plain_text, encrypt_text);
    display(encrypt_text);

    AesDecrypt(32, key_32, encrypt_text, decrypt_text);
    display(decrypt_text);
    
}

AES

AES

Mathematical Preliminaries

Finite Fields

Addition

Multiplication

Multiplication by x

Polynimials with Coefficients in GF( \(2^8\))

description

参数

State(s 数组)

Key Expansion

代码实现

cipher

流程分析

SubBytes

代码实现

ShiftRows()

代码实现

MixColumns()

代码实现：

AddRoundKey()

代码实现

解密

直接反向解密

Pseudo Code

完整代码：

`SubBytes`

`ShiftRows()`

`MixColumns()`

`AddRoundKey()`