记录一下读的三篇相关文章。
01. Representation Learning with Contrastive Predictive Coding
- arxiv:https://arxiv.org/abs/1807.03748 ,2018 年的文章。
- 参考博客:知乎 | 理解 Contrastive Predictive Coding 和 NCE Loss
- (发现 lilian weng 也写过 对比学习的博客 )
1.1 文章解读
这篇文章的主要思想是,我们维护一个 discriminator,负责判断两个东西是否是一致的(也可认为是一个判断相似性的函数);比如,我的 encoding 和我下一时刻的 encoding(这篇文章所做的),两个相同类别的样本,两个正样本,我的 encoding 和我数据增强后的 encoding 等等。
在这篇文章(CPC)里,我们定义 discriminator 是 \(f_k(x_{x+k},c_t)=\exp(z_{x+k}^TW_kc_t)\),这个函数大概计算了 z 和 c 的内积。其中,\(z_{x+k}\) 是 \(x_{x+k}\) 真实值的 encoding,而 \(c_t\) 是序列预测模型(比如说 RNN 或 LSTM)最后一步的 hidden 值,我们一般用这个值来预测。
这篇文章的 loss function 是
\[L_N = - E\left[\log\frac{f_k(x_{x+k},c_t)}{\sum _{x_j\in X} f_k(x_j,c_t)}\right] \]
这是一种 maximize [exp / Σ exp] 的形式。(照搬原博客)怎么理解这个 loss function 呢,\(p(x_{t+k}|c_t)\) 指的是,我们选正在用的那个声音信号的 \(x_{t+k}\) ,而 \(p(x_{j})\) 指的是我们可以随便从其他的声音信号里选择一个片段。
回忆一下,我们刚才说过, \(f_k()\) 其实是在计算 \(c_t\) 的预测和 \(x_{t+k}\) (未来值)符不符合。那么对于随便从其他声音信号里选出的 \(x_j\),\(f_k(x_j,c_t)\) 应是相对较小的。
在具体实践时,大家常常在对一个 batch 进行训练时,把当前 sample 的 \((x_{t+k}^i,c_t^i)\)(这里上标表示 sample 的 id)当作 positive pair,把 batch 里其他 samples 和当前 sample 的预测值配对 \((x_{t+k}^j,c_t^i)\) 作为 negative pair (注意上标)。
1.2 个人理解
这篇文章主要在说 InfoNCE loss。InfoNCE loss 大概就是 maximize [exp / Σ exp] 的形式,公式:
\[L_\text{InfoNCE} = - E\left[\log\frac{\exp(z^T_{x+k}Wc_t)}{\sum {x_j\in X} \exp(z^T{j}Wc_t)}\right] \]
这貌似是比较现代的对比学习 loss function。还有一些比较古早的 loss function 形式,比如 Contrastive loss(Chopra et al. 2005),它希望最小化同类样本(\(y_i=y_j\))的 embedding 之间的距离,而最大化不同类样本的 embedding 距离:
\[L(x_i,x_j) = \mathbb 1[y_i=y_j] \big\|f(x_i)-f(x_j)\big\| + \mathbb 1[y_i\neq y_j] \max\big(0,\epsilon- \|f(x_i)-f(x_j)\| \big) \]
第一项代表,如果是同类别样本,则希望最小化它们 embedding 之间的距离;第二项代表,如果是不同类样本,则希望最大化 embedding 距离,但不要超过 ε,ε 是超参数,表示不同类之间的距离下限。
Triplet Loss 三元组损失(FaceNet ,Schroff et al. 2015) :
\[L_\text{triplet}(x,x^+,x^-) = \sum_{x\in X} \max\big( 0, \|f(x)-f(x^+)\| - \|f(x)-f(x^+)\| + \epsilon \big) \]
其中,x 是 anchor,x+ 是正样本,x- 是负样本。我们希望 x 靠近 x+、远离 x-。可以理解为,我们希望最大化 \(\|f(x)-f(x^+)\| - \|f(x)-f(x^+)\| - \epsilon\) ,即,anchor 离负样本的距离应该大于 anchor 离正样本的距离,距离差超过一个超参数 margin ε。
02. CURL: Contrastive Unsupervised Representations for Reinforcement Learning
- arxiv:https://arxiv.org/pdf/2004.04136 ,ICML 2020。
- GitHub:https://www.github.com/MishaLaskin/curl
curl 也应用了这种 maximize [exp / Σ exp] 的形式,它的 loss function 是:
\[L_q=\log\frac{\exp(q^TWk_+)}{\exp(q^TWk_+) + \sum_{i=0}^{K−1}\exp(q^TWk_i)} \]
其中,q 是 query,貌似也可理解为 anchor,k 是 key,k+ 是正样本,ki 是负样本。anchor 和正样本 貌似都是图像裁剪得到的。
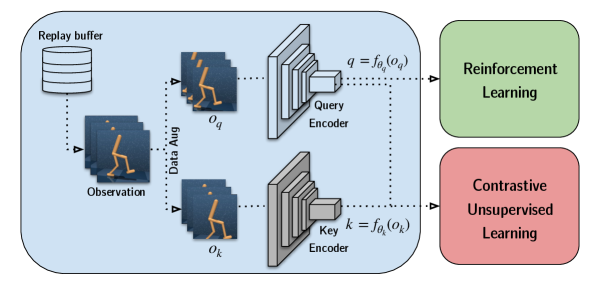
key encoder 的参数是 query encoder 的参数的 moving average,\(\theta_k=m\theta_k+(1-m)\theta_q\) 。
HIM 中,curl 是一个 baseline,HIM curl 的正样本是 adding gaussian perturbation ∼ N (µ = 0.0, σ = 0.1) 得到的。
03. Representation Matters: Offline Pretraining for Sequential Decision Making
做了很多 RL 相关的 representation learning 的 review 和技术比较,比较了各种实现在 imitation learning、offline RL 和 offline 2 online RL 上的效果。