DDPM(Denoising Diffusion Probabilistic Models)
论文研究背景
- 扩散概率模型(Denoising Diffusion Probabilistic Models, 简称DDPM)是近年来生成建模领域的重要发展之一。
- 生成模型的目标是学习数据分布并能够从中采样,生成与真实数据相似的新样本。
- 以往的生成模型主要有变分自编码器(VAE),生成对抗网络(GAN),自回归模型,正则化流(Normalizing Flows)等等。
- DDPM提供了一种全新的概率生成方法,结合了扩散过程的理论和深度学习的表达能力。
DDPM(Denoising Diffusion Probalistic Models)是扩散模型的基石。
扩散模型的研究并不始于DDPM,但DDPM的成功对扩散模型的发展起到至关重要的作用。

可以看到两边的图像都是DDPM所生成的图像,质量都非常不错,左边是清晰度较高的图像,右边是清晰度较低的图像
研究方法
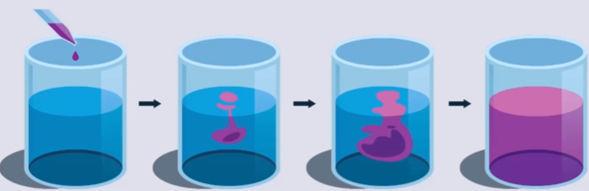
可以把DDPM的扩散过程比喻为一滴墨水滴到水杯的过程,墨水逐渐扩散直到完全扩散到整个水杯

DDPM的过程如上图所示,刚开始对原始图像进行前向加噪,噪声都是从高斯分布N(0,1)随机采样的噪声,最后直到原始图像完全变成了高斯噪声
然后再反向去噪,预测过程中所加的噪声,反向还原原始图像

上图是扩散模型的数学模型,可以看到原始图像的加噪过程是从\(x_{t-1}\)转移到\(x_t\)的概率分布,这是一个马尔可夫过程。马尔可夫分布具有无后效性。
反向去噪过程是一个参数化的马尔可夫链
研究方法
前向加噪
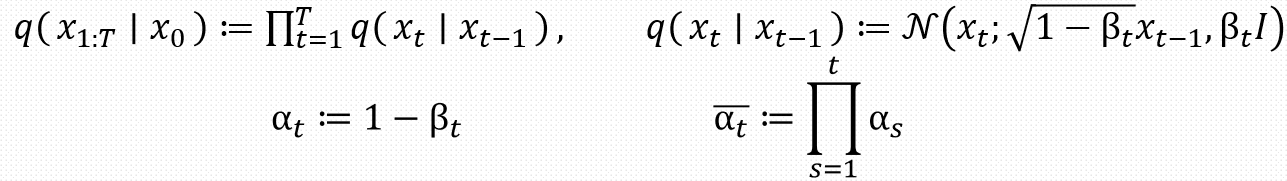
如图所示是论文中所提出的前向加噪过程部分公式,其中\(β_𝑡\) 随着𝑡增大是递增的,即\(β_1\)<\(β_2\)<...<\(β_𝑇\) 。\(β_𝑡\) 是由0.0001到0.02线性插值(以𝑇=1000为基准,𝑇增加,\(β_𝑡\) 对应增大)。
我们可以发现从\(x_{t-1}\)转移到\(x_t\)的概率分布是一个高斯分布,最后可以推出\(q(x_t \mid x_0) = \mathcal{N}(x_t; \sqrt{\bar{\alpha}_t} x_0, (1 - \bar{\alpha}_t) I)\)
推导过程如下所示:
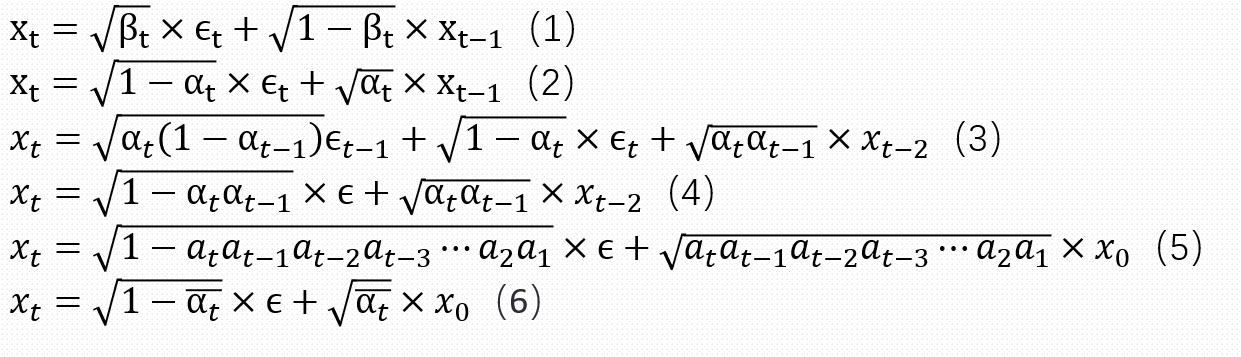
从公式1我们可以发现从前一张图片转移到后一张图片是一个线性加噪的过程,把\(β_t\)代换成\(α_t\)就可以得到公式2,紧接着我们可以把\(x_{t-1}\)展开成\(x_{t-2}\)的形式
公式4的推导是最为重要的,其中\(ϵ_(𝑡−1)\)和\(ϵ_𝑡\)都是独立的高斯噪声,根据高斯噪声的独立可加性和重参数化的技巧,最后可以合成公式4,然后继续迭代可以得到\(x_t\)和\(x_0\)的关系,可以发现它的均值和方差和论文最后所推出来的高斯分布相吻合。
反向过程
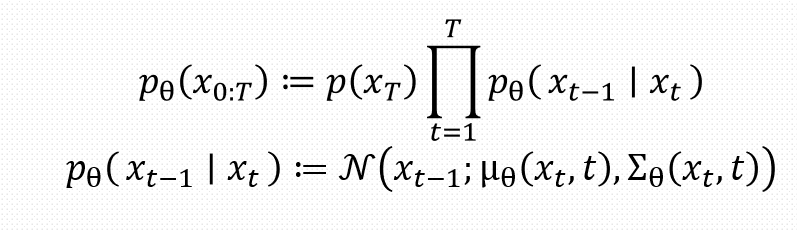
如图所示是反向过程所提出的部分公式,第一个公式根据马尔可夫的性质可以很容易得出来。
第二个公式可以看出来是一个带参数得高斯分布
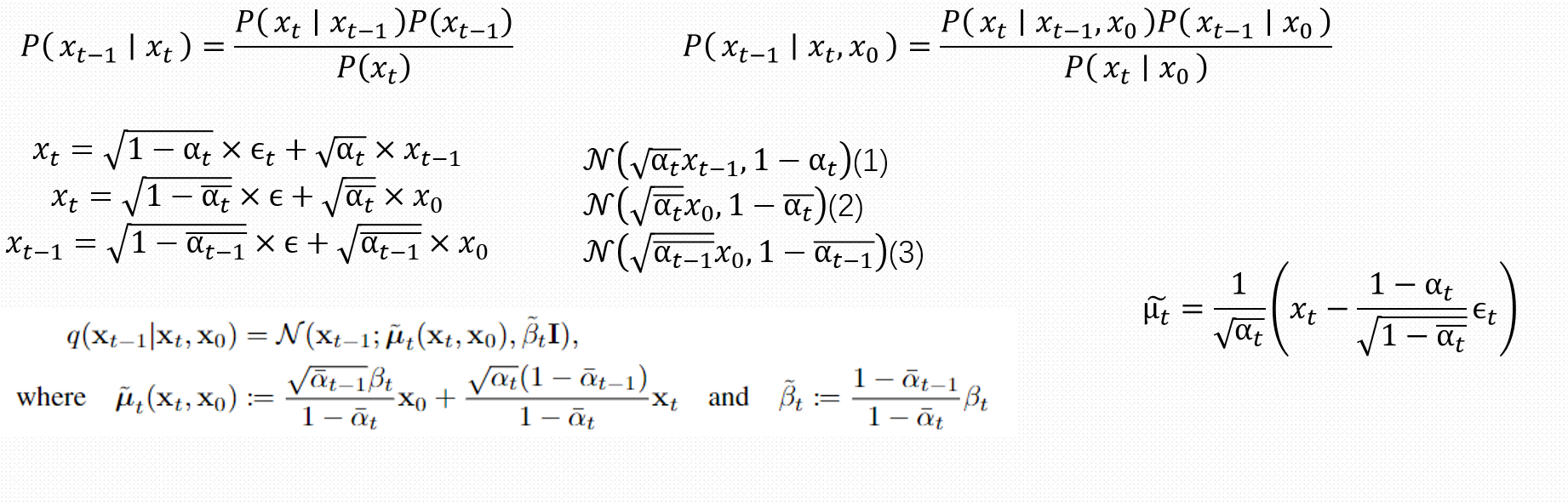
推导过程如上图所示,第一步主要使用了贝叶斯公式完成近似后验概率分布的推导,第二步为了简化引入了x0方便计算
可以看到第二步中的三个变量都是已知的,都是下面的三个已知分布,代入后可以得到论文中所得到的公式
最后可以得到\(\tilde{\mu}_t = \frac{1}{\sqrt{\alpha_t}} \left( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_t \right)\)
这就是我们需要去近似的参数,其中\(x_t\)是由\(x_0\)反代换出来的。
训练和采样过程

我们可以看到在训练过程中,每一次采样一个标准高斯分布的epsilon并将它和x0做前向加噪,最终的结果再变成输入进行后向去噪,其中\(\nabla_{\theta} \left\| \epsilon - \epsilon_{\theta} \left( \sqrt{\bar{\alpha}_t} \mathbf{x}_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon, t \right) \right\|^2\)是需要去优化的参数
在采样过程中,从\(x_t\)到\(x_{t-1}\)进行反向的去噪,其中的引入的z是为了引入随机化,使得最后生成的结果具有多样性。
\(\mathbf{X}_{t-1} = \frac{1}{\sqrt{\alpha_t}} \left( \mathbf{X}_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}t}} \boldsymbol{\epsilon}{\theta}(\mathbf{X}_t, t) \right) + \sigma_t \mathbf{Z}\)仔细观察公式,可以发现前半部分就是之前所推导出来的均值公式。
结果和分析
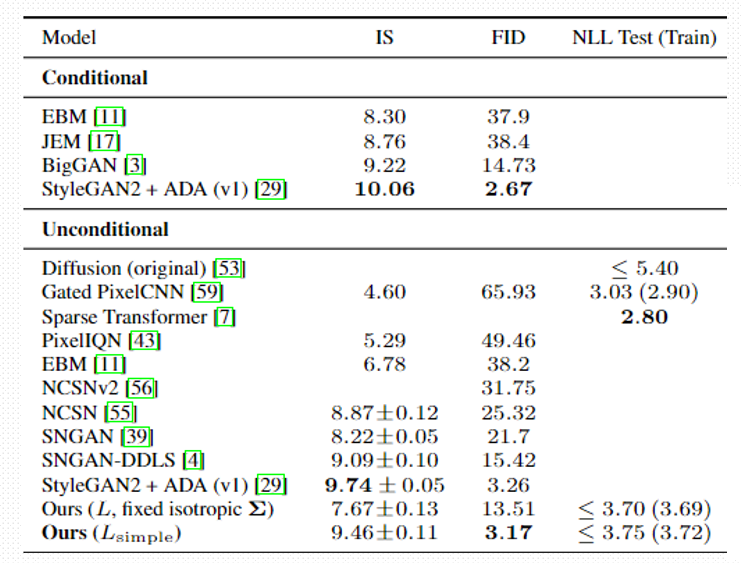
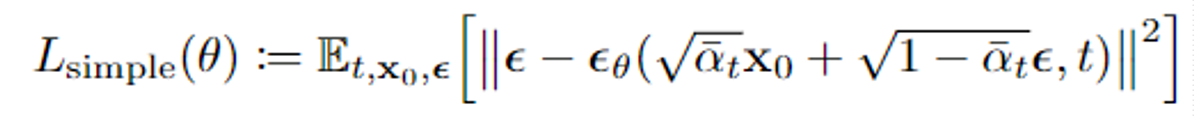
如图所示是该实验的实验结果,\(L_{simple}\)是最后所推出的损失函数,主要使用了变分推断下界,以及KL散度等,由于过于复杂,所以这里不再进行阐述
最后一行是实验的结果,其中IS分数越大越好,可以看到模型的IS分数仅次于倒数第三个模型,FID分数越低越好,模型的FID取得了显著的成果。
IS分数的解释
IS主要通过两个点衡量生成图片的质量
- 生成图像的单一标签分布清晰,说明图像质量高
- 生成图像在不同类别上分布多样,生成结果具有多样性。
Inception Score 的定义为:
\(IS(G) = \exp \left( \mathbb{E}{x \sim p_g} \left[ D{KL} ( p(y|x) \| p(y) ) \right] \right)\)
x~pg:生成图像样本来自生成模型的分布 。
p(y|x):通过预训练分类器(如 Inception 网络)对生成图像的类别预测概率分布。
p(y):预测类别的边缘分布。类别可以是猫,狗,猪等诸如此类的动物。
\(D_{KL}\):KL 散度,衡量两个分布的差异。
从公式出发有
\(\ln(IS(G)) = \mathbb{E}{x \sim p_g} D{KL}(p(y|x) \| p(y))\),KL散度公式为\(D_{KL}(p(y|x) \| p(y)) = \sum_y p(y|x) \ln \frac{p(y|x)}{p(y)}\)
代入后有\(\ln(IS(G)) = \sum_x p(x) \sum_y p(y|x) \ln \frac{p(y|x)}{p(y)}\),进行联合分布的替换,有\(\ln(IS(G)) = \sum_x \sum_y p(x, y) \ln \frac{p(y|x)}{p(y)}\)
互信息的公式为
\(I(y; x) = \sum_x \sum_y p(x, y) \ln \frac{p(x, y)}{p(x)p(y)}\)
\(I(y; x) = \sum_x \sum_y p(x, y) \ln \frac{p(y|x)}{p(y)}\)
所以有
\(\ln(IS(G)) = I(y; x)\)
\(I(y; x) = H(y) - H(y|x)\)
H(y)越高,则表明整体分布p(Y)多样,会更加接近均匀分布
H(y|x)越小,则表明生成图像x具有更高的置信度(分类器的确定性更高)。
IS分数的计算如下:
- 从生成图像G中进行采样大量图像
- 使用Inception预训练网络对生成图像进行分类,得到每个图像的类别概率分布p(y|x)
- 计算IS分数
FID分数的解释
主要是计算生成图像分布和真实图像分布在特征空间中的距离
公式\(\text{FID} = \| \mu_r - \mu_g \|_2^2 + \text{Tr}(\Sigma_r + \Sigma_g - 2 (\Sigma_r \Sigma_g)^{\frac{1}{2}})\)
\(\mu_r,\Sigma_r\):真实图像分布的均值和协方差矩阵。
\(\mu_g,\Sigma_g\):生成图像分布的均值和协方差矩阵。
\(\| \mu_r - \mu_g \|_2^2\):欧几里得距离的平方。
\(\text{Tr}\):矩阵的迹。
\((\Sigma_r \Sigma_g)^{\frac{1}{2}}\):协方差矩阵的乘积的平方根。
两个分布的均值和协方差越低,FID越低,生成图像质量越接近生成的图像
计算过程:
- 使用预训练的Inception v3网络,将真实图像和生成图像输入到网络中
- 提取某一层的特征向量(通常是倒数第二层),标记为高维特征表示
- 拟合高斯分布,分别计算均值和协方差矩阵
- 计算FID分数
插值

论文中还提到了插值的实验,首先我们先从源样本中采样出两张图片x0,x0',把两张图片进行前向加噪过程,变成xt,xt',可以进行进一步的平滑\(\overline{x_t} = (1 - \lambda) x_t + \lambda x_t'\),然后再进行后向去噪生成图像
观察上图,我们发现图像在生成的过程中在很多特征(如鼻子,眉毛,眼睛)等进行了平滑的变化,当\(\lambda\)等于1或0时,图片和原始的两张图像非常接近。
结论
- DDPM的损失函数采用了变分推导,优化过程更加稳定
- 采用了前向加噪和后向去噪的概率分布建模,具有严谨的概率意义。
- DDPM的反向去噪过程需要大量的计算,生成速度慢,且计算成本和采样成本更高