参考资料:
- VI参考:PRML Chapter 10.
- SGVI原文:Auto-Encoding Variational Bayes -- Kingma.
- VAE参考1:Tutorial on Variational Autoencoders -- CARL DOERSCH.
- VAE参考2:Stanford University CS236: Deep Generative Models.
泛函和变分法
本章主要是了解:"变分"这个名称是怎么来的。
函数和泛函
- 函数:值到值的映射;
- 泛函:函数到值的映射。
一个典型的泛函 ------ 熵的表达式:
\[H[p] = \int p(x) \ln p(x) \text{d}x \]
- 函数的导数:输入值发生极小变化时,输出值的变化。
- 泛函的导数:输入函数发生极小变化时,输出值的变化。
泛函的极值
- 求泛函的极值:遍历所有可能的函数,来找到最大化或者最小化泛函的那个函数。
- 变分法:研究泛函极值的方法。
- 在VI中,将隐变量模型的推断 问题转化成了求泛函极值 的问题,所以称它们是"变分"。
变分推断VI
本章讨论一种近似推断方法 -- 变分推断。
问题 -- 推断隐变量模型的Posterior和Evidence
符号表示
- \(Z\):隐变量,可以包括模型参数。
- \(X\):观测数据,显变量。
- \(P(Z)\):隐变量的先验概率,在这个问题中是已知的。
- \(P(X\mid Z)\):隐变量的似然概率,在这个问题中是已知的。
- \(P(X,Z)\):联合概率,可以直接\(P(X,Z)=P(X\mid Z)P(Z)\).
- \(P(Z \mid X)\):隐变量的后验概率,是需要求出来的。
- \(P(X)\):Marginal Evidence (或者就称作Evidence),是需要求出来的。
Tractable和Intractable
Tractable
典型例子如隐马尔可夫模型 (HMM),其主要特点:
- 只有有限个隐状态。
- 模型的结构简单。
所以模型参数已知时,可以直接用基于动态规划的精确推断方法:
- 求\(P(X)\):前向反向算法。
- 求\(P(Z\mid X)\):维特比算法。
Intractable
但是很多情况下:
- 涉及对连续随机变量积分。
- 模型结构很复杂。
此时想要精确推断通常intractable. 主要的困难就在于积分:\(P(X) = \int P(X,Z)\text{d}Z\).
因此需要使用近似推断方法。接下来介绍的是一种近似推断方法 ------ 变分推断。
ELBO的推导
考虑贝叶斯公式,在等式两边加上\(\log\):
\[\log P(X) = \log \frac{P(X,Z)}{P(Z|X)} =\log P(X,Z) -\log P(Z\mid X) \]
引入一个由\(\phi\)参数化的概率分布\(q_\phi(Z)\):
\[\begin{aligned} \log P(X) &= \log P(X,Z) -\log P(Z\mid X) \\ &= \log \frac{P(X,Z)}{q_\phi(Z)} - \log \frac{P(Z\mid X)}{q_\phi(Z)} \end{aligned} \]
等式两边同时对分布\(q_\phi(Z)\)求均值,可以得到:
\[\int_Z \log P(X) q_\phi(Z) \text{d} Z = \int_Z q_\phi(Z) \log \frac{P(X,Z)}{q_\phi(Z)}\text{d} Z - \int_Z q_\phi(Z) \log \frac{P(Z\mid X)}{q_\phi(Z)} \text{d}Z \]
由于左边\(\log P(X)\)和\(Z\)无关,可以直接提出来,又\(\int_Z q_\phi(Z) \text{d}Z =1\),所以有:
\[\log P(X) = \int_Z q_\phi(Z) \log \frac{P(X,Z)}{q_\phi(Z)}\text{d} Z - \int_Z q_\phi(Z) \log \frac{P(Z\mid X)}{q_\phi(Z)} \text{d}Z \]
将等式右边的第一项写成期望形式,第二项可以写成KL divergence的形式:
\[\begin{aligned} \log P(X)&= \mathbb E_{Z\sim q_\phi} [\log P(X,Z) - \log q_\phi(Z)] + KL(q_\phi(Z) \mid\mid P(Z\mid X)) \end{aligned} \]
观察这个式子,注意到以下性质:
- 由于\(KL\ge 0\),所以总有\(\log P(X) \ge \text{第一项}\),即第一项是\(\log\) Evidence的下界,简称为\(ELBO\) (Evidence Lower BOund).
- 当且仅当\(q_\phi(Z) = P(Z\mid X)\)时,\(KL=0\),此时\(\log P(X) = ELBO\).
- KEY1 :因此只需要找出\(\arg \max_{q_\phi}ELBO\),就可以使得\(ELBO\to \log P(X)\),同时会有\(KL \to 0\),此时就有\(q_\phi(Z) \to P(Z\mid X)\).
- KEY2 :一句话概括变分推断,就是将隐变量模型的推断问题 转化成了最优化 \(ELBO\)的问题。
REMARK1 :把\(ELBO\)看作一个泛函\(\mathcal L(q_\phi)\),目标就是\(\arg \max_{q_\phi} \mathcal L(q_\phi)\),即求泛函的极值点 (所以叫变分)。
REMARK2 :变分法天生不是近似方法,因为假如真的能够考虑到所有可能的函数,那就一定可以精确推断到后验概率。但是由于我们通常会对函数的范围做出假定 ,比如函数是二次型、或者函数满足平均场分解的条件,这导致了最后得出来的总是近似解。
REMARK3 :还有一种基于平均场理论 的对\(q(z)\)的假定,在此基础上可以利用坐标上升法求最优解,详情可以参考PRML Chapter10.
如果考虑单个样本
- \(X=\{x^{(1)},...,x^{(n)}\}\):观测变量。
假定每个样本独立同分布,则\(P(X)\)可以拆成连乘:
\[\log P(X) = \log \prod P(x^{(i)}) = \sum \log P(x^{(i)}) \]
引入一个由\(\phi^{(i)}\)参数化的分布\(q_{\phi^{(i)}}(Z\mid x^{(i)})\),\(\log P(x^{(i)})\)同样可以写成\(ELBO+KL\)的形式:
\[\begin{aligned} \log P(x^{(i)}) &= \int_Z q_{\phi^{(i)}}(Z\mid x^{(i)}) \log \frac{P(x^{(i)},Z)}{q_{\phi^{(i)}}(Z\mid x^{(i)})}\text{d} Z - \int_Z q_{\phi^{(i)}}(Z\mid x^{(i)}) \log \frac{P(Z\mid x^{(i)})}{q_{\phi^{(i)}}(Z\mid x^{(i)})} \text{d}Z \\ &= \mathbb E_{Z\sim q_{\phi^{(i)}}} [\log P(x^{(i)},Z) - \log q_{\phi^{(i)}}(Z\mid x^{(i)})] + KL(q_{\phi^{(i)}}(Z\mid x^{(i)}) \mid\mid P(Z\mid x^{(i)})) \\ &= ELBO +KL \end{aligned} \]
NOTE :\(q_\phi\)的参数\(\phi\)写作\(\phi^{(i)}\),是因为对于每单个观测变量来说,后验\(P(Z\mid x^{(i)})\)是不一样的。之后[[#SGVI]]章节中,为了表示简单,依然省略不写。
SGVI
上一章把隐变量的推断问题转化为了最优化\(ELBO\)问题,本章节讲估计\(ELBO\)梯度的方法。
- SGVI即随机梯度(stochastic gradient)变分推断,使用基于梯度的优化方法来最大化\(ELBO\).
- 求出梯度之后,\(q_\phi(z)\)参数更新:\(\phi = \phi + \alpha \nabla_\phi ELBO\).
Score function gradient estimator
\(ELBO\)对\(\phi\)的梯度形如\(\nabla_\phi \mathbb E_{z\sim q_\phi(z)}[f(z)]\),下面先分析这个更一般化的形式的梯度:
\[\nabla_\phi \mathbb E_{z\sim q_\phi(z)}[f(z)] = \nabla_\phi \int q_\phi(z) f(z) \text{d}z \]
把梯度符号移入积分号,然后由于\(\nabla \log q_\phi=\frac{\nabla q_\phi}{q_\phi}\),可得:
\[\begin{aligned} \nabla_\phi \mathbb E &= \int \nabla_\phi q_\phi(z) f(z) \text{d}z \\ &= \int q_\phi(z) \nabla_\phi \log q_\phi(z) f(z) \text{d}z \\ &= \mathbb E_{z\sim q_\phi(z)}[f(z) \nabla_\phi \log q_\phi(z)] \end{aligned} \]
等式右边的期望可以直接使用MC采样来估计:
\[\mathbb E_{z\sim q_\phi(z)}[f(z) \nabla_\phi \log q_\phi(z)] \approx \frac{1}{L} \sum_{l=1}^L f(z^{(l)}) \nabla_\phi \log q_\phi(z^{(l)}) \]
- \(z^{(l)}\sim q_\phi(z)\).
- 这个估计方法被称作score function gradient estimator,其中\(\nabla_\phi \log q_\phi(z)\)被称作是score,\(f(z)\)被称作是cost.
- 这个estimator存在的问题是:方差太大 ,很多时候都用不了,也不适合直接拿来估计\(ELBO\).
NOTE :我们实际上假定了\(q_\phi(z)\)是tractable的,既容易采样 又容易计算。
BTW :强化学习中的REINFORCE算法 中,估计策略梯度用的就是这个estimator,所以我们会说REINFORCE是一种方差很大的算法。
Reparameterized trick
采样过程\(z\sim q_\phi(z\mid x)\),通常可能分解成以下两个步骤:
- 先从一个noise分布中采出\(\epsilon \sim p(\epsilon)\).
- 然后找出一个由\(\phi\)参数化的函数\(g_\phi(,)\),使得\(z=g_\phi(\epsilon, x)\).
比如说从正态分布采样\(z\sim \mathcal N(\mu, \sigma)\),就可以拆分成:
- \(\epsilon \sim \mathcal N(0,1)\).
- \(z = \mu + \epsilon \sigma\).
以上就是重参数化技巧。
SGVI estimator
在使用重参数化技巧之后,可以把期望的表达式写成以下形式:
\[ \mathbb E_{z\sim q_\phi(z\mid x^{(i)})}[f(z)]=\mathbb E_{\epsilon \sim p(\epsilon)}[f(g_\phi(\epsilon, x^{(i)}))] \approx \frac{1}{L} \sum_{l=1}^L f(g_\phi(\epsilon^{(l)},x^{(i)})) \]
令\(f=ELBO\),再求梯度,就得到了SGVI estimator:
\[\nabla_\phi ELBO=\nabla_\phi \mathcal L(\phi,x^{(i)}) = \nabla_\phi \bigl(\frac{1}{L}\sum_{l=1}^L \log P(x^{(i)},g_\phi(\epsilon^{(l)},x^{(i)})) - \log q_\phi(g_\phi(\epsilon^{(l)},x^{(i)})\mid x^{(i)}) \bigr) \]
其中\(\epsilon^{(l)}\sim p(\epsilon)\).
NOTE:SGVI estimator通常会比score function gradient estimator有更小的方差。
变分自编码器VAE
本章讨论VI方法是如何应用到隐变量生成模型的推断和学习中的。
样本的分布
我们常常希望生成和数据集中的数据相似的样本。比如说给一个人脸数据集,我们希望模型能够通过某种方式学习这批人脸数据的分布,然后能够再通过某种方式生成出人脸来。
-
对样本的假定 :通常会假定数据集是从一个未知分布\(P_{gt}(X)\)采样出来的.
-
理解 :如果一张图片\(X\)有人脸的样子,那么\(P_{gt}(X)\)就很大;如果一张图片\(X\)都是噪声,那么\(P_{gt}(X)\)就很小。
-
我们的目的 :找到一个可以采样的模型\(P(X)\),同时\(P\)能够尽可能逼近\(P_{gt}\).
-
如何学习模型参数 :假设参数化的模型\(P_\theta(X)\),要学习参数\(\theta\),就是要让模型在已经观测到的数据\(X\)上,概率最大,即:\(\arg \max_\theta P_\theta(X)\) (Max Likelihood).
隐变量生成模型
考虑使用隐变量生成模型来逼近\(P_{gt}\).
引例:以生成数字为例,一种思考方法
- 模型先确定\({0,1,...,9}\)范围的一个数字\(z\).
- 然后再基于\(P(X\mid z;\theta)\)从\(z\)生成对应数字的图片。
这里的\(z\)就是隐变量。
困难:确定隐变量,再确定隐变量和观测变量的关系,这个过程实际上可能很复杂:
- 比如模型可能要先确定要生成的数字里有没有圆圈 (0, 8, 9),再确定圆圈的数量。
- 除此之外,还可能需要确定数字的倾斜度、字体等更复杂的关系。
考虑用如下方法来克服:
- 直接假定隐变量服从高斯先验分布\(z \sim \mathcal N(0,I)\).
- 假定模型也是一个高斯分布\(P(X\mid z;\theta)=\mathcal N(X\mid \mu_\theta(z),\sigma_\theta(z))\),其参数是关于\(z\)的函数。
- 参数\((\mu_\theta(z), \sigma_\theta(z))\)都使用神经网络来建模。
为什么这样做:
- KEY1:简单的高斯分布,经过足够复杂的非线性变换,就可以表示出任意的分布。
- KEY2 :由于神经网络可以建模任意复杂的非线性关系 ,所以最后可以表示出任意我们想要的分布。
- Example:对高斯分布做非线性变换。左边是高斯分布,右边是\(g(z) = \frac{z}{10} + \frac{z}{||z||}\).
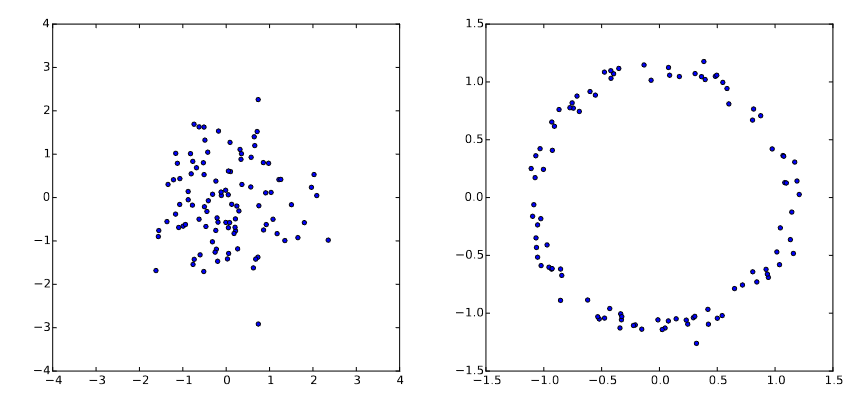
因此得到我们用来近似真实数据分布\(P_{gt}(X)\)的模型\(P(X;\theta)\):
\[P(X;\theta) = \int P(X,z;\theta)\text{d}z =\int P(X\mid z;\theta) P(z) \text{d}z =\int \mathcal N(X\mid \mu_\theta,\sigma_\theta) \mathcal N(0,I)\text{d}z \]
- 可以认为这个模型的表示能力是足够的。
- \(z\)对我们来说是不可观测的隐变量,所以需要考虑所有可能\(z\) (体现在积分).
- 是很复杂的模型,推断模型的Marginal Evidence \(P(X;\theta) = \int P(X,z;\theta)\text{d}z\)、学习模型参数\(\arg \max_\theta P(X;\theta)\),都很困难。
模型的近似推断和学习
考虑使用变分推断的近似方法。
根据[[#变分推断VI]]部分的讨论,可以将模型的\(\log\) Evidence写成\(ELBO+KL\)的形式:
\[\begin{aligned} \log P(x^{(i)};\theta) &= \mathbb E_{z\sim q_{\phi^{(i)}}} [\log P(x^{(i)},z;\theta) - \log q_{\phi^{(i)}}(z)] + KL(q_{\phi^{(i)}}(z) \mid\mid P(z\mid x^{(i)};\theta)) \end{aligned} \]
主要区别:带上了模型参数\(\theta\).
NOTE :现在最大化\(ELBO\),既需要考虑近似分布\(q\)的参数\(\phi\),也需要考虑模型参数\(\theta\).
NOTE :此时,最大化\(ELBO\)同时具有两个作用:
-
推断:最小化了\(KL\),使得\(q\)逼近真实后验分布 ;
-
学习:最大化了Evidence,相当于做了MLE,使得模型\(P_\theta\)逼近真实数据分布 \(P_{gt}\).
再根据[[#SGVI]]部分的讨论,使用SGVI estimator来估计\(ELBO\):
\[\nabla \mathcal L(x^{(i)},\phi^{(i)},\theta)=\nabla \bigl(\frac{1}{L}\sum_{l=1}^L \log P(x^{(i)},g_{\phi^{(i)}}(\epsilon^{(l)},x^{(i)});\theta) - \log q_{\phi^{(i)}}(g_{\phi^{(i)}}(\epsilon^{(l)},x^{(i)})) \bigr) \]
- \(g_\phi(\epsilon^{(l)},x^{(i)})\)是重参数化后的\(z\).
- \(\epsilon \sim p(\epsilon)\).
- 梯度算子\(\nabla = \{\nabla_\phi, \nabla_\theta\}\).
讨论至此,可以得到模型的学习过程如下:

Amortized Inference
- 上方学习过程的一个缺点:对于每个\(x\),都要先推断出一个足够好的\(q_{\phi^*}\).
- KEY :近似推断后验概率 = 学习后验概率的参数 (这个视角是由VI提供的)。
Amortized Inference:考虑引入一个参数化的函数\(f_\lambda: x^i \to \phi^*\),它会学习 如何根据\(x^i\)确定一个足够好的\(\phi^*\). 即对于每个\(x^i\),都会得到后验\(q(z;f_\lambda(x^i))\).
如何学习?同样是重参数化+梯度上升。
因此,得到更简化的模型学习过程:
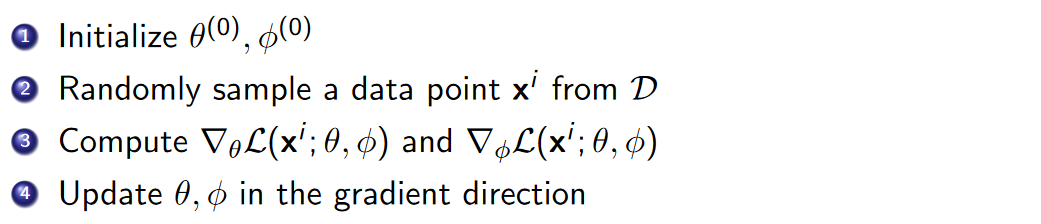
NOTE :直到[[#Amortized Inference]]这一小节截止,才开始有了Encoder-Decoder结构的雏形,即\(x^i\to q(z;f_\lambda(x^i)) \to z \to P(X\mid z;\theta) \to \bar x^i\).
对Objective的解析
训练VAE是以最大化\(ELBO\)为目标,这一小节从\(ELBO\)本身的形式,讨论\(ELBO\)的实际意义。
这里推导用的是符号简化版的\(ELBO\)表达式:
\[\begin{aligned} ELBO &= \int q_\phi(Z)\log P(X,Z) - q_\phi(Z)\log q_\phi(Z) \text{d}Z \\ &= \int q_\phi(Z)\log P(X\mid Z) + q_\phi(Z) \log P(Z) - q_\phi(Z)\log q_\phi(Z) \text{d}Z \\ &=\int q_\phi(Z)\log P(X\mid Z) + q_\phi(Z) \log \frac{P(Z)}{q_\phi(Z)}\text{d}Z \\ &= \int q_\phi(Z)\log P(X\mid Z) \text{d}Z + \int q_\phi(Z) \log \frac{P(Z)}{q_\phi(Z)}\text{d}Z \\ &=\mathbb E_{q_\phi}[\log P(X\mid Z)] - KL(q_\phi(Z)\mid\mid P(Z)) \end{aligned} \]
可以看到\(ELBO\)两项的意义:
- 第一项 :可以看作是Loss项,意义是极大似然,表示我们想要生成的\(X\)和数据集尽可能相似。
- 第二项 :可以看作是正则化项,意义是希望后验尽可能接近已知的先验\(P(Z)\),这表明我们想要从\(P(Z)\)随机抽一个\(z\),就大概率能生成有意义的结果。
VAE结构示例
下面是由前馈神经网络实现Encoder、Decoder的VAE的结构示意图。左图是无重参数化技巧的,右图是有重参数化技巧的。
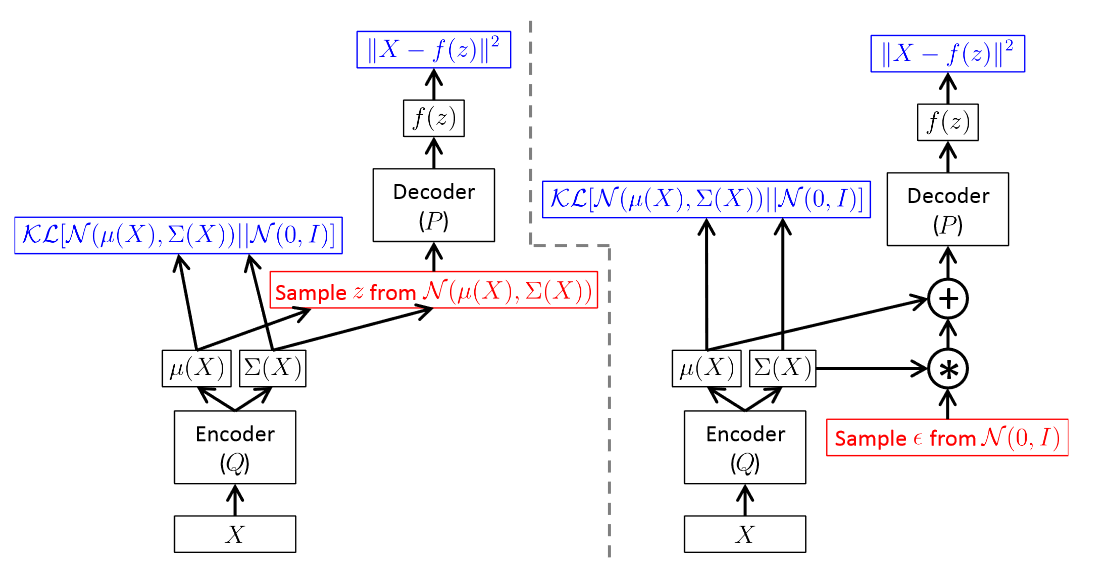
几个要点:
- 网络输出 :Decoder从隐变量\(z\)重建\(\bar X\);Encoder输出\(q_\phi(z\mid X)\),即从\(X\)压缩到隐变量。
- 重参数化和Autodiff:重参数化技巧使得autodiff可以将误差从Decoder一直传回到输入。
- Objective的选择 :不必严格是\(ELBO\)
- Loss项:要能体现Reconstruction error,根据问题的不同可以灵活选择。
- 正则项:除了KL散度外,也可以采用其他的散度。
- 关于生成 :Decoder部分才是我们的隐变量生成模型。随机从\(\mathcal N(0,I)\)中抽取\(z\),再输入到Decoder中,就可以生成样本。
参考代码
以下是基于CNN的VAE实现。
Encoder
python
class Encoder(nn.Module):
def __init__(self, num_channels, hidden_size):
super(Encoder, self).__init__()
# 输入是(batch_size, num_channels, 28, 28),就是MNIST数据集的形状
self.conv1 = nn.Conv2d(num_channels, 32, 4, 2) # (28 - 4) / 2 + 1 = 13
self.conv2 = nn.Conv2d(32, 64, 4, 2, 1) # (13 - 4 + 1) / 2 + 1 = 6
self.conv3 = nn.Conv2d(64, 128, 4, 2) # (6 - 4) / 2 + 1 = 2
self.fc_mu = nn.Linear(128 * 2 * 2, hidden_size)
self.fc_logstd = nn.Linear(128 * 2 * 2, hidden_size)
def forward(self, x):
x = F.relu(self.conv1(x))
x = F.relu(self.conv2(x))
x = F.relu(self.conv3(x))
x = torch.flatten(x, start_dim=1)
mu = self.fc_mu(x)
log_std = self.fc_logstd(x)
return mu, log_stdDecoder
python
class Decoder(nn.Module):
def __init__(self, num_channels, hidden_size):
super(Decoder, self).__init__()
self.fc1 = nn.Linear(hidden_size, 512)
self.deconv1 = nn.ConvTranspose2d(512, 64, 5, 2)
self.deconv2 = nn.ConvTranspose2d(64, 32, 5, 2)
self.deconv3 = nn.ConvTranspose2d(32, num_channels, 4, 2)
def forward(self, x):
x = F.relu(self.fc1(x))
x = x.unsqueeze(-1).unsqueeze(-1) # num -> [[num]]
x = F.relu(self.deconv1(x))
x = F.relu(self.deconv2(x))
reconstruction = F.sigmoid(self.deconv3(x)) # output (0, 1)
return reconstructionVAE
python
class VAE(nn.Module):
def __init__(self, num_channels, hidden_size):
super(VAE, self).__init__()
self.encoder = Encoder(num_channels, hidden_size)
self.decoder = Decoder(num_channels, hidden_size)
def forward(self, x):
mu, log_std = self.encoder(x)
z = self.reparameterize(mu, log_std)
reconstruction = self.decoder(z)
return reconstruction, mu, log_std
def reparameterize(self, mu, log_std):
std = log_std.exp()
eps = torch.randn_like(std)
return mu + std * epsLoss
python
def vae_loss(x, reconstruction, mu, log_std):
# 图像生成,使用BCE的效果会比较好
rec_loss = F.binary_cross_entropy(reconstruction, x, reduction='sum')
# 这里是化简后的q和N(0, I)的KL散度表达式
kl_loss = -0.5 * torch.sum(1 + 2 * log_std - mu.pow(2) - (2*log_std).exp())
return rec_loss + kl_loss