探秘Transformer系列之（2）---总体架构

0x00 概述

0.1 流程

使用Transformer来进行文本生成其实就是用模型来预测下一个词，完整流程包括多个阶段，如分词、向量化、计算注意力和采样，具体运作流程如下：

分词（tokenize）。把用户的输入文本（此处假设是"Data visualization empowers users to"）拆解为若干独立的词汇单元，即token。
编码。借助词表把token映射为数字，每个token由一个唯一的数字表示。
embedding（嵌入）化。embedding模块将token代表的数字转换为embedding向量，即将词映射到一个向量空间，这样LLM才能处理。此时还会加上位置编码信息，因为理解语言不仅关乎单词，还关乎单词的顺序。位置编码可以确保单词的顺序不会丢失。所有嵌入向量组合在一起形成嵌入矩阵。
注意力计算。这是语境化操作，若干堆叠的Transformer Block通过注意力机制将这些Embedding向量转换成若干特征向量，构建词和词之间的关系。在注意力计算过程中，每个token可以了解自己与其它token的相关性。最终每个token流经Transformer最后一层之后得到的是一个代表语义的特征向量。
计算概率。将最后一个token（"to"）对应的特征向量映射为下一个待预测词的概率分布（logits）。具体操作是通过一个线性层把特征向量升维到词表维度（即把解码器的输出转化为与词典大小相同的向量），并且通过softmax进行归一化，最终输出一个概率分布。该分布表示对词表中每个词匹配这个特征向量的概率。
采样。依据这些概率，按照一定的采样规则来采样下一个token，比如选取概率最高的"visualize"作为最有可能出现的下一个单词。
再次使用分词表将"visualize"对应的整数转换回原始的词汇，形成推理结果句子。
不断重复上述过程。直到LLM输出结束流（EOS）标记表示解码结束或者已经生成所需数量的token。

下图将上述流程的核心部分作了可视化，也是本篇讲解的基础，后续将对模型结构和执行流程进行逐步细化。

0.2 说明

本系列主要以下面几项为基础：

Transformer论文：Attention Is All You Need https://arxiv.org/abs/1706.03762v7。
其它相关经典论文和精彩博客，参考将在各个篇幅的具体部分中给出。
"The Annotated Transformer" 博客以及其源码（后续简称为哈佛源码）。"The Annotated Transformer" 是Transformer论文的读书笔记，而且博客作者用代码实现了论文的模型，并且结合实现的模型对原始论文做了详细解读。与互联网上可以获取的其他Transformer的模型实现相比较，"The Annotated Transformer" 更适合学习和解读。其地址为：
- http://nlp.seas.harvard.edu/2018/04/03/attention.html
- https://github.com/harvardnlp/annotated-transformer.git 2025年-2月4日拉取其代码。

另外，本篇以文本翻译功能为例来进行说明。

0x01 总体架构

1.1 设计动机

Transformer的新颖之处在于它是一个完全基于注意力机制实现的序列转换架构，我们对Transformer的主要设计动机分析如下：

解决长距离依赖关系。论文希望解决RNN在序列长距离上的限制，而注意力机制可以将序列中的任意两个位置之间的距离是缩小为一个常量，从而在长文本分析时可以捕获更多的语义关联关系。
提升训练并行度。论文希望克服RNN不能并行的缺点，而注意力机制可以无视序列的先后顺序来捕捉序列间的关系，因此具有更好的并行性，符合现有的GPU框架，能够进行分布式训练，提升模型训练效率。

因此，Jakob Uszkoreit（Transformer作者之一）提出了用自注意力机制来替换RNN对序列的编解码过程。而Noam Shazeer（Transformer作者之一）在此基础上提出了scaled dot-product attention、多头注意力和位置表示。

1.2 模型结构

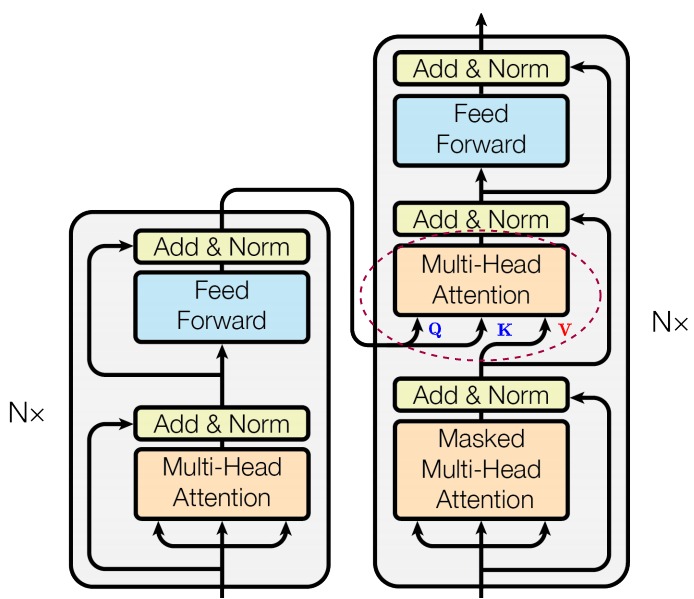
首先我们来看看原始论文里面的架构图，接下来就以它为源头进行分析。

主体模块

从网络结构来分析，Transformer 包括了四个主体模块。

输入模块，对应下图的绿色圈。
编码器（Encoder），对应下图的蓝色圈。
解码器（Decoder），对应下图的红色圈。编码器和解码器都有自己的输入和输出，编码器的输出会作为解码器输入的一部分（位于解码器的中间的橙色圈）。
输出模块，对应下图的紫色圈。

确切的说，蓝色圈是编码器层（Encoder layer），红色圈是解码器层（Decoder layer）。图中的 $N\times$ 代表把若干具有相同结构的层堆叠起来，这种将同一结构重复多次的分层机制就是栈。为了避免混淆，我们后续把单个层称为编码器层或解码器层，把堆叠的结果称为编码器或解码器。在Transformer论文中，Transformer使用了6层堆叠来进行学习。

多层

在Transformer中，第一层的输入是嵌入矩阵。第一层的输出随后被用作第二层的输入，依此类推。每一层都生成了一组嵌入，但这些嵌入不再直接与单个词元相关，而是与某种更复杂的词元关系的理解相关联。比如下图给出了一个模型中的第6层和第7层之间的关系，该模型每层有12个注意头。

对于多层的作用，目前也有不同的解释。比较常见的解释是分层的本质是由下往上从不同上下文中逐步构建不同层次的特征。比如底层学习单词特征，中间层学习句法特征，高层学习语义特征等，每一层做各自的事情，不会相互影响。

输入文本对应的embedding在Transformer内部各层流通时会不断演变，这个过程类似于逐层"精炼"和"抽象"输入的信息。每一层都会对输入进行不同级别的变换和抽象，都会在其输入的基础之上吸收更多上下文信息来丰富自己的表示，逐层提取出更高层次的特征，从而在综合多层之后就会获得更加强大的表达能力。随着深度学习模型进行训练，这些网络层会逐渐学习到各种范畴之间的关系和相似性，从而在推理和回答问题时能够利用这些知识。当embedding到达最后一层时，其不仅仅代表对应token独立的含义，而是具备深刻的语境信息，反应了该token与序列中其它token的综合关系。我们可以把多层加工理解为工厂的流水线，假定要生产一件瓷器，我们要先通过印坯和修坯来确定器物形状，然后通过刻花来在已经干了的坯体上刻画出各种精美的花纹或者图案。接下来进行施釉，在成型的陶瓷坯体表面施以釉浆；最后将瓷坯装入匣钵，高温入窑烧造。最终才能得到一件精美的瓷器。

针对分层中的每一层可能都会起到不同的作用这点，研究人员做了深入的研究。

论文"What Does BERT Learn about the Structure of Language?"剖析了 BERT 所理解的英语结构的复杂性。他们的研究发现，BERT 的短语表示主要在神经网络的较低层捕捉短语级别的信息，并在中间层中编码了语言要素的复杂层次结构。这个层次结构以表层特征作为基础，中间层提取语法特征，最上层呈现语义特征。

论文"Analyzing Memorization in Large Language Models through the Lens of Model Attribution"指出：

较深层的注意力模块（最后25%的层）主要负责记忆。
较浅层的注意力模块对模型的泛化和推理能力至关重要。
在深层注意力模块应用短路（short-circuit）干预可以显著降低记忆所需内存，同时保持模型性能。

论文"Interpreting Key Mechanisms of Factual Recall in Transformer-Based Language Models"则发现。语言模型存在一种普遍机制：防止过度自信（anti-overconfidence）：在模型的最后若干层，语言模型总是在抑制正确答案的输出。这种抑制具体又分为两种：

通过注意力头将输入起始位置的信息复制到了最末位置，我们发现起始位置的信息似乎包含了很多高频的token，模型可以通过这种方法来让高频token稀释残差流中的正确回答，降低回答的自信度。
末层的MLP似乎在将残差流引导向一个"平均"token的方向（平均token是基于训练数据的词频，对token embedding加权平均得到的结果）。

另外，模型的效果往往和模型的参数量成正比，Transformer就是通过增加模型的层数来加大模型可学习的参数量，让更多的参数来承载文本中深层次的信息。

1.3 注意力模块

注意力机制是Transformer模型的心脏，它赋予模型洞察句子中每个单词与其它单词间错综复杂关系的超能力。

分类

在Transformer中有三种注意力结构：全局自注意力，掩码自注意力和交叉注意力，具体如下图所示。交叉注意力主要用于处理两个不同序列之间的关系；全局自注意力主要用于处理单个序列内元素之间的关系；掩码自注意力（也被称做因果自注意力）通过掩码来控制模型在计算注意力分数时的关注范围，从而确保在解码时不会受到未来信息的影响。

位置

三种注意力模块在Transformer网络对应位置如下图所示。

作用

Transformer实际上是通过三重注意力机制建立起了序列内部以及序列之间的全局联系。论文中对这三种注意力作用的解释如下图所示。

我们具体分析下这三种注意力。

全局自注意力层

全局自注意力层（Global self attention layer）位于编码器中，它负责处理整个输入序列。在全局自注意力机制中，序列中的每个元素都可以直接访问序列中的其它元素，从而与序列中的其他元素建立动态的关联，这样可以使模型更好地捕捉序列中的重要信息。自注意力的意思就是关注于序列内部关系的注意力机制，那么是如何实现让模型关注序列内部之间的关系呢？自注意力将query、key、value设置成相同的东西，都是输入的序列，就是让注意力机制在序列的本身中寻找关系，注意到不同部分之间的相关性。

对于全局自注意力来说，Q、K、V有如下可能：

Q、K、V都是输入序列。
Q、K、V都来自编码器中前一层的输出。编码器中的每个位置都可以关注编码器前一层输出的所有位置。

再细化来说，Q是序列中当前位置的词向量，K和V是序列中的所有位置的词向量。

掩码自注意力

掩码自注意力层或者说因果自注意力层（Causal attention layer）可以在解码阶段捕获当前词与已经解码的词之间的关联。它是对解码器的输入序列执行类似全局自注意力层的工作，但是又有不同之处。

Transformer是自回归模型，它逐个生成文本，然后将当前输出文本附加到之前输入上变成新的输入，后续的输出依赖于前面的输出词，具备因果关系。这种串行操作会极大影响训练模型的时间。为了并行提速，人们引入了掩码，这样在计算注意力时，通过掩码可以确保后面的词不会参与前面词的计算。

对于掩码自注意力来说，Q、K、V有如下可能：

Q、K、V都是解码器的输入序列。
Q、K、V都来自解码器中前一层的输出。解码器中的每个位置都可以关注解码器前一层的所有位置。

再细化来说，Q是序列中当前位置的词向量，K和V是序列中的所有位置的词向量。

交叉注意力层

交叉注意力层（Cross attention layer）其实就是传统的注意力机制。交叉注意力层位于解码器中，但是其连接了编码器和解码器，这样可以刻画输入序列和输出序列之间的全局依赖关系，完成输入和输出序列之间的对齐。因此它需要将目标序列作为Q，将上下文序列作为K和V。

对于交叉注意力来说，Q、K、V来自如下：

Q来自前一个解码器层，是因果注意力层的输出向量。
K和V来自编码器输出的注意力向量。

这使得解码器中的每个位置都能关注输入序列中的所有位置。另外，编码器并非只传递最后一步的隐状态，而是把所有时刻（对应每个位置）产生的所有隐状态都传给解码器，这就解决了中间语义编码上下文的长度是固定的问题。

或者从另一个角度来理解，交叉注意力是序列到序列模式；双向自注意力是自编码模式；单向自注意力是自回归模式。

1.4 执行流程

我们再来结合模型结构图来简述推理阶段的计算流程，具体如下图所示。

假设我们进行机器翻译工作，把中文"我吃了一个苹果"翻译成英文"I ate an apple"，在假设模型只有一层，执行步骤如下：

处理输入。用户输入自然语言句子"我吃了一个苹果"；tokenizer先把序列转换成token序列；然后Input Embedding层对每个token进行embedding编码，再加入Positional Encoding（位置编码），最终形成带有位置信息的embedding编码矩阵。编码矩阵用 $X_{n*d}$ 表示， n 是句子中单词个数，d 是表示向量的维度（论文中 d=512）。注：原论文图上的输入是token，本篇为了更好的说明，把输入设置为自然语言句子。
编码器进行编码。编码矩阵首先进入MHA（Multi-Head Attention，多头注意力）模块，在这里每个token会依据一定权重把自己的信息和其它token的信息进行交换融合；融合结果会进入FFN（Feed Forward Network）模块做进一步处理，最终得到整个句子的数学表示，句子中每个字都会带上其它字的信息。整个句子的数学表示就是Encoder的输出。
通过输入翻译开始符来启动解码器。
解码器进行解码。解码器首先进入Masked Multi-Head Attention模块，在这里解码器的输入序列会进行内部信息交换；然后在Multi-Head Attention模块中，解码器把自己的输入序列和编码器的输出进行融合转换，最终输出一个概率分布，表示词表中每个单词作为下一个输出单词的概率；最终依据某种策略输出一个最可能的单词。这里会预测出第一个单词"I"。
把预测出的第一个单词"I"和一起作为解码器的输入，进行再次解码。
解码器预测出第二个单词"ate"。

针对本例，解码器的每一步输入和输出具体如下表所示。

1.6 小结

Transformer总体架构是一个有机整体，难以分割。组合的意义不在于构成它的基本单元，而在于这些单元之间形成的复杂关系和涌现的行为。比如集体智能来自个体的组合，却产生了所有个体都不具备的高阶能力。

有些工作就将焦点转移到 transformer 模块的高级架构上，并认为其完整结构，而不仅仅是标记混合注意力操作，对Transformer实现具有竞争力的性能至关重要。

论文"Attention is not all you need"指出如果没有skip connection（residual connection-残差链接）和MLP，自注意力网络的输出会朝着一个rank-1的矩阵收缩。即，skip connection和MLP可以很好地阻止自注意力网络的这种"秩坍塌（秩坍塌）退化"。这揭示了skip connection，MLP对self-attention的不可或缺的作用；

论文"MetaFormer is Actually What You Need for Vision"则描述了一种通用架构，在该结构中，输入首先经过embedding，得到 𝑋。然后embedding送入重复的blocks中，第一个block主要包含了token mixer，使得不同的token能够相互信息通信（Y = TokenMixer(Norm(X)) + X,）；第二个block包含两层MLP。该架构通过指定token mixer的具体设计，可以获得不同的模型。如果将token mixer指定为注意力或spatial MLP，则MetaFormer将分别成为一个transformer或类似MLP的模型。

0x02 构建

我们接下来结合哈佛源码进行分析和学习。哈佛代码中的make_model()函数是Transformer模型的构建函数。

2.1 参数

make_model()函数的参数有如下7个：

src_vocab：源语言词表中单词数目，即源词典的大小。
tgt_vocab：目标语言词表中单词数目，即目标词典的大小。
N=6：编码器和解码器堆叠数，即编码器层数和解码器层数。
d_model=512：模型所处理数据的维度，即词向量（word embedding）的大小。
d_ff=2048：FFN（前馈全连接层）中变换矩阵的维度，即隐层神经元的数量。
head=8：多头注意力层中的注意力头数。
dropout=0.1：防止过拟合。

2.2 构建逻辑

make_model()函数的主要思路就是用从小到大搭建积木的方式来构建Transformer。我们先脱离代码来构思下，看看架构图上的哪些模块可以作为积木。

输入模块：Input Embedding和Positional Encoding分别可以作为单独的积木块，它们结合在一起又可以作为一个新的积木块。
编码器层和解码器层可以作为两个单独的大积木块。其内部的Masked Multi-Head Attention、Multi-Head Attention、Feed Forward和Add & Norm也都可以作为单独的小积木块。
输出模块：Linear和Softmax分别可以作为单独的积木块，它们结合在一起又可以作为一个新的积木块。

有了这些积木块，我们就可以很容易的构建起Tranformer了。当然，在make_model()函数中做了一定的抽象，有些小积木块被用某些类进行了封装（比如Linear和Softmax被封装在Generator类中，细节没有在make_model()函数中展示出来）。我们把这些模块和代码中一一对应起来看，下图中的数字代表代码中某模块出现的顺序，这些数字在下面代码的注释中也有标明。

具体的代码逻辑如下。

把copy.deepcopy()这个深度拷贝函数重新命名为c，这样后续代码会比较简洁。deepcopy()函数会开辟一个新内存并将源实例完全复制过来，复制过来的对象和源对象没有任何关联。后续各种类的构造函数中会调用copy.deepcopy()来重新生成一个对应实例，比如上面图中的标号1，2，3在解码器端就分别被做了深度拷贝。这样，两个标号1对应的实例彼此之间相互独立，不受干扰。
构建 MultiHeadedAttention，PositionwiseFeedForward 和 PositionalEncoding 对象。
构造 EncoderDecoder 对象，这是Transformer主体类，其参数是Encoder、Decoder、src-embed、tgt-embed和 Generator。我们先分析后面三个参数。
- src-embed是nn.Sequential(Embeddings(d_model, src_vocab), c(position))的返回结果，其意义是输入编码，对应上图的编号7（由编码3和6组成）。nn.Sequential()函数构建了顺序容器，容器内模块的顺序就是模型处理数据的顺序；
- tgt-embed是nn.Sequential(Embeddings(d_model, tgt_vocab), c(position))的返回结果，其意义是输入编码，对应上图的编号9（由编码3和8组成）。
- Generator对应上图的编号10，其包括了Linear和Softmax。Generator会把Decoder的输出变成输出词的概率。
Encoder和Decoder两个类很像，我们以Encoder为例来说明。Encoder由N个EncoderLayer构成，EncoderLayer的参数是d_model, c(attn), c(ff), dropout，即word embedding维度、多头注意力、FFN层和Dropout。可以看到，Encoder和Decoder类中的注意力都是MultiHeadedAttention的实例，只是因为传递参数的不同，才决定某个注意力是交叉注意力还是掩码多头注意力。
初始化模型参数。Xavier初始化可以参考论文"Understanding the difficulty of training deep feedforward neural networks"。

具体代码如下。

python 复制代码

def make_model(src_vocab, tgt_vocab, N=6, d_model=512, d_ff=2048, h=8, dropout=0.1):
    "Helper: Construct a model from hyperparameters."
    # copy.deepcopy是深度拷贝函数，即重新生成一个新实例。重新命名可以让后续代码比较简洁
    c = copy.deepcopy
    # 构建多头注意力层的实例，对应上图的数字标号1
    attn = MultiHeadedAttention(h, d_model)
    # 构建前馈神经网络层的实例，对应上图的数字标号2
    ff = PositionwiseFeedForward(d_model, d_ff, dropout)
    # 构建位置编码模块的实例，对应上图的数字标号3
    position = PositionalEncoding(d_model, dropout)
    # 总的Transformer模型
    model = EncoderDecoder(
        # EncoderLayer只包含一个Attention层，对应上图的数字标号4。Encoder则包括外面的N
        Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
        # DecoderLayer包含两个Attention层，对应上图的数字标号5，Decoder则包括外面的N
        Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),
        # 输入的Embedding和位置编码，Embeddings对应上图的数字标号6，Sequential就是两个编码合并的结果，对应上图的数字标号7
        nn.Sequential(Embeddings(d_model, src_vocab), c(position)),
        # 输出的Embedding和位置编码，Embeddings对应上图的数字标号8，Sequential就是两个编码合并的结果，对应上图的数字标号9
        nn.Sequential(Embeddings(d_model, tgt_vocab), c(position)),
        # Generator类包括Linear层和Softmax层，对应上图的数字标号10，负责依据Decoder的输出来预测下一个token
        Generator(d_model, tgt_vocab),
    )

    # This was important from their code.
    # Initialize parameters with Glorot / fan_avg.
    # 初始化模型参数，这里采用xavier初始化，即如果参数的维度大于1，则将其初始化成一个服从均匀分布的矩阵
    for p in model.parameters():
        if p.dim() > 1:
            nn.init.xavier_uniform_(p)
    return model

2.3 主体类

EncoderDecoder类就是基于Transformer架构的编码器-解码器实现，其成员变量如下：

encoder：Encoder类实例，这是编码器的实现。
decoder：Decoder类实例，这是解码器的实现。
src_embed：源语言的word embedding生成模块，是一个nn.Sequential对象，包括Embebddings和PositionalEncoding。src_embed将对输入进行Embedding和位置编码
tgt_embed：目标语言的word embedding生成模块，是一个nn.Sequential对象，包括Embebddings和PositionalEncoding。tgt_embed将对再传入的输出进行Embedding和位置编码
generator：Generator类的对象，包括Linear层和Softmax层，负责对Decoder的输出做预测，即依据Decoder的隐状态输出来预测当前时刻的词。隐状态会输入到全连接层（全连接层的输出大小是词典的大小），全连接层会接上一个softmax得到预测词的概率。

EncoderDecoder类的forward()函数完成了编码和解码的工作，它接受四个函数：

src：源序列，其内容是token在词表对应的编号。src的形状是[batch_size, seq_len]，举例是[[ 0, 2, 4, 8, 1, 2, 2 ]] ，即批量大小为1，句子长度是7，其中0为bos，1为eos，2为pad。
tgt：目标序列，具体含义类似src。
src_mask：源序列掩码，具体作用是对填充符号进行掩码。以[[ 0, 2, 4, 8, 1, 2, 2 ]]为例，其掩码是[[True,True,True,True,True,False,False]]，即对两个填充的pad进行掩码。
tgt_mask：目标序列掩码，其作用有两种：不让注意力计算看到未来的单词；对填充符号进行掩码。其形状是[batch_size, seq_len, seq_len]，上面对应的掩码如下：

python 复制代码

[True,False,False,False,False,False,False],
[True,True,False,False,False,False,False],
[True,True,True,False,False,False,False],
[True,True,True,True,False,False,False],
[True,True,True,True,True,False,False], # 例句是5个正式token，后面两个pad被置为False
[True,True,True,True,True,False,False],
[True,True,True,True,True,False,False],

EncoderDecoder代码具体如下：

python 复制代码

# 继承nn.Module
class EncoderDecoder(nn.Module):
    """
    A standard Encoder-Decoder architecture. Base for this and many other models.
    标准的编码器-解码器架构，这是很多模型的基础。
    """

    def __init__(self, encoder, decoder, src_embed, tgt_embed, generator):
        """
        初始化函数有5个参数，从外部传入参数的目的是更加灵活，可以更换组件
        """
        super(EncoderDecoder, self).__init__()
        self.encoder = encoder # 编码器对象
        self.decoder = decoder # 解码器对象
        # 源语言input embedding和position embedding的组合
        self.src_embed = src_embed 
        # 目标语言output embedding和position embedding的组合
        self.tgt_embed = tgt_embed 
        self.generator = generator # 类别生成器对象

    def forward(self, src, tgt, src_mask, tgt_mask):
        # 前向传播函数有四个参数：源序列，目标序列，源序列掩码，目标序列掩码
        "Take in and process masked src and target sequences."
        # 1. 将source, source_mask传入编码函数encode()，让编码器对源序列进行编码，得到编码结果memory
        # 2. 将memory，source_mask，target，target_mask一同传给解码函数decode()进行解码
        return self.decode(self.encode(src, src_mask), src_mask, tgt, tgt_mask)

    # 编码函数，接受参数是源序列和掩码
    def encode(self, src, src_mask):
        # 1. 对src编码，得到input embedding
        # 2. 计算位置编码，将input embedding和位置编码相加，得到word embedding
        # 3. 使用编码器encoder进行编码，编码结果记作memory
        return self.encoder(self.src_embed(src), src_mask)

    # 解码函数，参数为：编码器输出（memory）、源序列掩码、目标序列和目标序列掩码
    def decode(self, memory, src_mask, tgt, tgt_mask):
        # 1. 对tgt编码，得到得到input embedding
        # 2. 计算位置编码，将input embedding和位置编码相加，得到word embedding
        # 3. 使用编码器decoder进行解码，解码器输出可以使用self.generator进行最后的预测
        return self.decoder(self.tgt_embed(tgt), memory, src_mask, tgt_mask)

2.4 如何调用

模型调用的方式如下面代码所示，forward()函数负责把输入编码成隐状态，然后把隐状态解码称输出logits（对数几率）。其参数都从batch类的实例中获取，具体如下：

src：源句子列表。形状是[batch size, max sequence length]。每个句子是从数据集提取出来，经过词典处理过的，举例为：[ 0, 5, 12,..., 1, 2, 2]。其中0为bos，1为eos，2为pad。
tgt：目标句子列表。具体意义同上。
src_mask：注意力层要用的掩码（后面章节会详细分析）。
tgt_mask：解码器的掩码自注意力层要用的掩码（后面章节会详细分析）。

python 复制代码

out = model.forward(batch.src, batch.tgt, batch.src_mask, batch.tgt_mask)

0x03 输入

3.1 输入分类

我们还是用把中文"我吃了一个苹果"翻译成英文"I ate an apple"为例。模型的总体输入是若干个单词组成的句子，不同模型支持的句子最大长度不同，如果句子较短，则会用某些特殊词填充多余的位置。而源语言和目标语言（或者说编码器和解码器）分别对应了两种不同的独立的输入。

编码器的输入对应图上的Inputs，这是从原始的源序列文本得到的token列表。在机器翻译业务中，Encoder是一次性接受一个完整的句子，然后进行处理。比如"我吃了一个苹果"这几个字经过tokenizer之后，得到了每个字对应的唯一序号，假设序号为[5, 4, 6,7, 8, 9, 10]，然后会把[5, 4, 6,7, 8, 9, 10]作为inputs传给Encoder层。
解码器的输入其实有两种：
- Outputs(shifted right)。Outputs实际上是解码器之前输出的拼接，shifted right的目的是将序列整体右移一位。解码器并不能一次性全部输出"I ate an apple"，而是一个单词一个单词进行输出，或者说是像RNN一样循环执行的，也就是这次的输出（作为Outputs）会加到上次的输入后面，作为下一次的输入，以便生成后续的单词。
- 编码器的输出。编码器层把Inputs编码成一个中间隐状态（在Transformer实现中叫做memory，对应了RNN的Hidden State）输出给解码器，或者说是编码器把源语言的完整句子一次性编码输出给解码器。

具体如下图所示。

3.2 输入模块

输入模块具体包括如下：

Tokenizer（词元分析器）。注：原论文图上的输入是token，本篇为了更好的说明，把输入设置为自然语言句子，也加入了tokenizer。
源语言文本嵌入层（对应图上的 Input Embedding）和位置编码器（对应图上的Positional Encoding）。
目标语言文本嵌入层（对应图上的Output Embedding）和位置编码器（对应图上的Positional Encoding）。

3.3 文字转换

回到本篇最开始图1的例子。"Data visualization empowers users to"这个句子并不能被模型理解，因此我们需要把自然语言进行编码，也就是对文字进行向量化。具体分为以下几个步骤：

对输入文字进行tokenize（分词），得到token。
在词表（假设词表大小是10000）中找到每个token对应的token id。
把每个token id转化成一个token embedding（假设维度是512）。
给序列中的每个位置添加一个位置编码。
把input embedding和位置编码相加，得到最终的word embedding。

具体流程如下。

让我们看看每个步骤是如何完成的。

分词

分词是将输入文本分解为更小、更易于管理的语义片段的过程，这些片段被成为token。token是模型词汇表的一部分，词汇表是LLM在训练时使用的词元列表。tokenizer（分词器）会做两件事：

首先，tokenizer会将输入文本切分为更小、更易于管理的token。token可以是单词或子词（sub-word），比如单词"Data" 就被映射成token，而单词 "empowers" 则被分为两个token："em"和"powers"。
接下来，tokenizer会把token映射成不同的整数，这些整数就是词表的索引。可以认为这是一种one-hot编码形式。

embedding化

我们接下来看看在NLP领域中，词嵌入向量生成过程，即如何把单词在词表里面的索引转换为一个Transformer可以使用的向量，也就是embedding（嵌入）。embedding是每个词元的固定向量表示，它比纯整数更适合深度学习，因为它捕捉到了单词的语义意义。embedding向量的大小取决于模型维度。当输入中每个token的embedding堆叠在一起时，它们构成了输入的嵌入矩阵。

在Transformer架构图中，Inputs和Outputs的上面分别有一个Embedding模块，每个模块都是由两个子模块组合而成。

Inputs相关的embedding模块包括Input Embedding和Positional Encoding。
- Input Embedding负责把token编码。
- Positional Encoding负责给token加入位置信息。实际操作中，Transformer会一次性接收整个输入句子的嵌入矩阵。这样做的好处是可以并行操作，但是劣势是缺少位置信息，比如模型无法区分"我爱你"和"爱你我" 。Positional Encoding就负责给每个词增加位置信息。
Outputs相关的embedding模块包括Output Embedding + Positional Encoding：与上面类似，不再赘述。

Token Embedding

Token Embedding会将文字转换成模型可以理解和处理的数学表示，即将每个token id（one-hot）和一个高维向量相关联，向量的每个维度对应语义的某个方面。embedding通常是查表操作，即根据token_id的值，去embedding矩阵中查找第token_id行的数据作为embedding。向量的维度取决于模型，Transformer论文将每个token表示为512维向量。Token Embedding也叫word embedding。

Positional Encoding

一个句子中的文字先后顺序很重要，比如以下两句话的文字完全相同，但因为文字顺序不同，其语义完全不同。

买一张从上海到北京的车票。
买一张从北京到上海的车票。

因此，模型还需要对输入句子中每个token的位置信息进行编码。

Word Embedding

最后，模型将token embedding和Positional Encoding相加，得到最终的嵌入表示。这种组合表示捕获了标记的语义及其在输入序列中的位置。在 LLM（大型语言模型）中，将 word embedding（词嵌入）加上位置编码后的结果通常仍可以称为 "输入嵌入（Input Embeddings）" 或 "带位置信息的词嵌入"。为了讲述方便，后续我们依然称之为Word Emebdding 。

本阶段输出张量的形状是[batch size, sequence length,embedding dimension]。以"Data visualization empowers users to"为例，5个单词被切分成6个token，最终得到的word embedding是一个[batch size， sequence length, embedding dimension]的矩阵。因为只有一句话，所以batch size是1，sequence length是6，假设embedding dimension是512，则矩阵维度是[1,6,512]。

实际上，我们可以认为embedding是LLM自己的语言系统（包括文本信息特征空间与位置信息特征空间）。输入层的作用就是把自然语言、程序语言、视觉听觉语言等信息都映射（或者叫编码）到这个高维的语言空间中。接下来会通过注意力机制从高维语言空间中提取各种丰富的知识和结构，加权积累与关联生成自己的语言，最后再"编码"回人类的语言。

0x04 Transformer Layer

Transformer处理的核心在于Transformer块，它包括多头注意力机制和多层感知器层。大多数模型由多个这样的块组成，这些块一个接一个地顺序堆叠。

从Transformer的构造代码可以看出来，Encoder类实例是由N个EncoderLayer类实例构建而成，Decoder类实例由N个DecoderLayer类实例构建而成，这和论文相符合。

python 复制代码

# EncoderLayer只包含一个注意力层，Encoder则包括外面的N参数
Encoder(EncoderLayer(d_model, c(attn), c(ff), dropout), N),
# DecoderLayer包含两个注意力层，Decoder则包括外面的N参数
Decoder(DecoderLayer(d_model, c(attn), c(attn), c(ff), dropout), N),

EncoderLayer和DecoderLayer是基础构建块，每个块主要包括如下：

多头注意力机制。它允许token与其他token进行通信，彼此交流信息，从而捕获上下文信息和单词之间的关系。
FFN层。一个对每个token 独立运行的前馈网络。注意力层的目标是在 token 之间路由信息，而 MLP 的目标是细化每个 token 的表示。

本小节先概要介绍多头自注意力机制和FFN层，后续篇幅会对EncoderLayer和DecoderLayer进行详细介绍。

4.1 多头自注意力机制

自注意力机制使模型能够专注于输入序列的相关部分，从而使其能够捕获数据内的复杂关系和依赖关系。多头注意力机制借鉴了CNN中multi-kernel 的思想，对不同头使用不同的线性变换。多头自注意力机制本质上是构造多个子空间，在这些子空间上再构建多个注意力来替代单个注意力，这样可以获取更多维度的信息和相互关系。自注意力机制是LLM架构中唯一计算序列中词元间关系的地方，因此它构成了语言理解的核心，涵盖了对词汇关系的理解。

让我们看看多头自注意力机制如何计算。为了简化说明，这里假设编码器也用到了掩码，对于某些复合操作也分解说明。

第 1 步：根据原始嵌入计算查询、键和值矩阵

自注意力机制的输入是n_tokens x n_embd的嵌入矩阵，其中每一行或向量表示一个独立的词元。LLM计算的第一部分从词元嵌入矩阵中提取每个词元的相关行。每个 token 的word embedding被转换为三个不同的向量，分别称为query、 key和 value。这些向量是通过将输入嵌入矩阵与学习到的$W^Q$、 $W^K$和 $W^V$权重矩阵相乘（这些矩阵是模型参数的一部分）得出的。query和key的点积被用来来判断两个向量之间的相似性，这也是论文中提到的点积注意力。

我们用淘宝搜索来类比，可以帮助我们对这些矩阵有更好的理解。假如我们在淘宝上进搜索"李宁鞋"。

query是你在搜索栏输入的查询内容。
key是在页面上返回的商品描述、标题，其实就是淘宝商品数据库中与候选商品相关的关键字。
value是李宁鞋商品本身。因为一旦依据搜索词（query）搜到了匹配的商品描述、标题（key），我们就希望具体看看商品内容。

通过使用这些 QKV 值，模型可以计算注意力分数，从而确定每个token在生成预测时应从其它token那里获得多少关注。

第 2 步：掩码自我注意力

掩码自注意力允许模型通过关注输入的相关部分来生成序列，同时防止访问未来的token。下图展示了如何使用查询、键和值矩阵来计算掩码自注意力。

图上具体分为三步：

使用点积来计算注意力分数。使用Q和K矩阵的点积来决定了每个Q与每个K的对齐程度，点积结果是一个反映所有输入token之间关系的矩阵。
对注意力分数施加scaling（缩放）和掩码。首先对注意力分数进行缩放，其次将掩码应用于注意力矩阵的上三角，以防止模型访问未来的标记，因为模型需要学习如何在不"窥视"未来的情况下来预测下一个token。
施加Softmax和dropout操作。注意力分数会通过 softmax 运算转换为概率，然后会施加dropout操作来随机丢弃一些元素。

此时得到的结果是注意力权重。

第3步：拼接

使用第二步产生的权重和V矩阵进行相乘以获得自注意力机制的最终输出，因为是多头注意力的结果，所以需要把这些头的输出进行拼接并且通过线性层来融合。

4.2 FFN层

在多个自注意力头捕获输入token之间的不同关系后，拼接的输出将通过FFN（feed-forward network）层进行处理，以增强模型的表示能力。下图展示了如何使用 FFN层将自注意力表示投影到更高的维度，以增强模型的表示能力。

FFN层由两个线性变换组成，线性变换中间有一个激活函数。第一个线性变换将输入的维度从512 增加到四倍2048。第二个线性变换将维度降回到的原始大小512，以确保后续层接收到维度一致的输入。

与自注意力机制在序列中彼此交流不同，FFN对序列中每个元素都独立计算，因此不会进行元素间的信息交换（元素间的互动完全靠自注意力）。这样有助于在注意力层进行元素间的信息交换之后，让每个元素消化整合自己的信息，为下一层再次通过自注意力交换信息做好准备。

4.3 辅助架构

除了上述主要模块之外，Transformer模型中还应用了LayerNorm（层归一化）和ResNet（残差连接）等设计方法。虽然在上面源码中的构造函数中没有提及，但这些模块对提高模型的整体表示能力非常重要。

LayerNorm

LayerNorm有助于稳定训练过程并提高收敛性。它的工作原理是对输入的各个特征进行归一化，确保激活的均值和方差一致。普遍认为这种归一化有助于缓解与内部协变量偏移相关的问题，使模型能够更有效地学习并降低对初始权重的敏感性。从架构图上看，LayerNorm在每个Transformer 块中应用两次，一次在自注意力机制之后，一次在FFN层之后，但是在实际工作中不一定如此。

Dropout

Dropout 是一种正则化技术，用于通过在训练期间随机将一部分模型权重设置为零来防止过拟合。这鼓励模型学习更强大的特征并减少对特定神经元的依赖，帮助网络更好地泛化新的、未见过的数据。

残差连接

残差连接（Residual Connection）于 2015 年首次由何凯明大神在ResNet论文中引入。残差连接就是把网络的输入和输出相加，得到网络的新输出为F(x)+x。其本质思想是允许网络中的信息和梯度直接跨过一个或多个层进行传播，这样能够保留原始的一些信息。这种架构创新可以有助于缓解梯度消失问题，从而训练更深的神经网络，彻底改变了深度学习Transformer论文中，残差连接在每个 Transformer 块内使用两次：一次在FFN之前，一次在 FFN之后。

0x05 概率输出（Output Probabilities）

经过一系列Transformer模块的精心处理，输入数据最终来到了它的归宿------最后的输出层。输出模块包括两部分：线性层和softmax层。哈佛代码用Generator类对这两部分进行了封装，将模型输出的 embeding 转换为对下一个词的预测（在整体词表上的概率分布）。

5.1 解码器结果

输入经过所有解码块处理后，最终输出依然是若干token对应的向量，其代表在Transformer视角下的，用高维概率向量编织起来事物之间的各种复杂关系。这些关系在本质上就是范畴论概念下事物的米田嵌入（米田嵌入采用对象的所有关系来表征该对象）。Transformer 学习的过程，是核函数选择与参数化的过程，也是寻找米田嵌入的过程：提取对象的所有关系，形成其关系图 -- 即概率化的内部世界模型。

我们首先看看哈佛代码。在推理时，generator使用的并不是编码器的所有输出，而是最后一个token对应的向量out[:, -1]，即只使用输出序列中最后一个单词的猜测结果。训练时，generator则使用编码器的全部输出。下面是推理代码示例。

python 复制代码

def inference_test():
    test_model = make_model(11, 11, 2)
    test_model.eval()
    src = torch.LongTensor([[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]])
    src_mask = torch.ones(1, 1, 10)

    memory = test_model.encode(src, src_mask)
    ys = torch.zeros(1, 1).type_as(src)

    for i in range(9):
        out = test_model.decode(
            memory, src_mask, ys, subsequent_mask(ys.size(1)).type_as(src.data)
        )
        prob = test_model.generator(out[:, -1])
        _, next_word = torch.max(prob, dim=1)
        next_word = next_word.data[0]
        ys = torch.cat(
            [ys, torch.empty(1, 1).type_as(src.data).fill_(next_word)], dim=1
        )

下面是训练代码示例。

python 复制代码

class SimpleLossCompute:
    "A simple loss compute and train function."

    def __init__(self, generator, criterion):
        self.generator = generator
        self.criterion = criterion

    def __call__(self, x, y, norm):
        x = self.generator(x)
        sloss = (
            self.criterion(
                x.contiguous().view(-1, x.size(-1)), y.contiguous().view(-1)
            )
            / norm
        )
        return sloss.data * norm, sloss

5.2 转换

Transformer的输出是最有可能放在输入序列末尾的单词。但输出的最后一个token对应的向量是512维的向量，无法直接用来推理。另外，词表中每个单词都有可能成为下一个单词，所以模型需要对所有它知道的单词均按可能性打分，最终选出其中最合适的单词推荐给用户。因此我们最终需要得到词表中所有单词作为下一个单词的概率。这需要经历几个阶段才能完成从512维向量得到10000个单词概率的转换。

在 "Embedding"部分，我们已经学习了一种映射，它可以将给定的（one-hot）单词转换为 512 向量，然后才能被Transformer处理。现在编码器-解码器已经处理结束，所以需要反转这个映射（求逆），将输出的 512 向量转换回词表对应的10000 维度空间中。可以理解为，对于最后一个token向量来说有一个分类任务，需要把该向量分类到词表中的正确token，即下一个token的分类。Transformer通过一个线性层达到了这个目的，从向量维度投影到词表长度（[1，embed_size]->[1，vocab_size]）。其中词汇表中的每个token都有一个对应的值，称为 logit。该过程类似CNN中，卷积层之后再接一个线性层做分类。
因为是要预测，所以需要根据模型的输出 logits 为词汇表中的每个token分配一个概率。这些概率决定了每个token成为序列中下一个单词的可能性。具体操作是应用 softmax 函数将 logits 转换为总和为 1 的概率分布。

下图中的Output Probabilities就是线性层后经过Softmax的概率分布，红圈对应就是Generator类。后续会根据这些标记成为下一个单词的可能性对其进行采样。比如我们可以简单地根据对它们进行排名。从中得到最大的值对应的index，然后再去字典中查询，就知道预测的下一个词是什么了，即得到了下一个词在词典中的编号。

简而言之，这最后的线性层和softmax函数共同作用，为模型预测下一个词提供了数学基础和概率指导。

在后续的文章中，我们会逐步深入Transformer的各个组成模块。

0x06 解释

对于Transformer，迄今为止，我们所了解的更多是实践的成果和经验性的积累，而对于其理论和理解非常缺乏甚至是空白。虽然有些东西我们直观上操作没问题，但是我们有必要看看研究人员如何从理论（机器学习、生物学和数学）角度进行的探索。这些探索试图从本质上理解神经网络和Transformer内部运作的机理，看看其为何是一个好的结构，从而从这个理解角度出发来帮助分析失败案例，探索设计出更好的网络结构和有效的训练方法，减少模型的偏见、幻觉等。也可以使Transformer能够更好的应对提示的长度和复杂性，可以在更有限的计算资源下完成复杂任务，进而为 NLP 领域的发展提供新的思路和方法。

注：以下分类并非是正交的，可能会有彼此交叉。因为数学的具象化为物理，而物理的尽头则为数学，数学与物理相辅相成，成为理解神经网络乃至智能本质不可或缺的手段。

6.1 机械可解释性

近年来，机械可解释性（Mechanistic Interpretability）成为AI可解释性研究的一个重要方向，该可解释性研究旨在以逆向工程方式剖析AI模型（尤其是黑盒子的神经网络模型），希望理解LLM内部的运行机制，以及定位参数的存储位置。机械可解释性的几个主要流派如下：

causal tracing。主要目标是理解LLM的信息流机制。基本思想是当改变模型的某个位置的参数/向量时，查看最终预测的变化情况，通过变化程度定位到对最终输出最重要的位置。
circuit analysis。主要目标是以注意力头和FFN作为基本单元，构建输入到输出的circuit。它的潜在假设是：对于特定的输入/输出，只有一小部分参数很重要。比如该研究中有一部分是探索不同注意力头的功能，另一部分专注于构建整个circuit。
logit lens & neuron analysis。更强调从单个神经元角度进行分析。logit lens把LM head提前加在每个中间layer上，以此观察latent embeddings的特性。也有其它工作把神经元投影到unembedding space中来获取可解释性。
SAE（sparse autoencoder）。这是Anthropic的工作，目的是使用SAE来增加神经元的可解释性。

我们以causal tracing和circuit analysis为例来看看有关研究思路。

causal tracing

理解语言模型的内部运作意味着定位前向传播中的哪些元素（输入元素、表示和模型组件）负责特定的预测。我们接下来介绍几种定位模型行为的不同方法。

稀疏探测

论文"Finding Neurons in a Haystack: Case Studies with Sparse" 提出了稀疏探测，这是一种旨在识别与特定特征相关的 LLM 神经元的技术或概念，并有助于理解高级人类可解释的特征如何在此类模型的神经元激活中表示。

该团队使用自回归LLM，针对 k 个神经元来施加探针来看它们的分类性能。他们将主要发现总结如下：

LLM 的神经元内有大量可解释的结构，稀疏探测是定位此类神经元（即使处于叠加状态）的有效方法，但需要仔细使用和后续分析才能得出严格的结论。
许多早期层神经元处于叠加状态，其中特征表示为多语义神经元的稀疏线性组合，每个神经元都会激活大量不相关的 n-gram 和局部模式。此外，根据权重统计和玩具模型的见解，论文得出结论，前 25% 的全连接层比其余层使用更多的叠加。
更高层次的上下文和语言特征（例如，is_python_code）似乎是由单语义神经元编码的，而且主要发生在中间层。
表示稀疏性随着模型规模的增加而增加，但不同的特征服从不同的动态：一些具有专用神经元的特征随着规模增加而出现；有的特征分裂成具有规模的更细粒度的特征；许多特征保持不变或随机出现。

输入归因

输入归因方法通常用于通过估计输入元素（在LM的情况下为token）在模型预测中的贡献来定位模型行为。

下图给出了在注意力头间计算令牌间贡献的三种方法。仅依赖注意力权重会忽略它们所操作的向量的大小。这种限制可以通过考虑值加权或输出值加权向量（$x′_j$）的范数来解决，即第二种方法。最后，基于距离的分析根据加权向量与注意力输出的接近程度来估计加权向量的贡献。

模型组件归因

直接逻辑归因（DLA，Direct Logit Attributions）是一种解释词汇空间中模型组件输出激活的技术。DLA应用未嵌入矩阵来模拟内部激活，有效地跳过了下游组件的进一步计算。下图给出了在输出token w上应用DLA 的案例。分别是(a)注意头的DLA；(b)通过注意头的中间表示的DLA；(c)FFN块的DLA和(d)单个神经元的DLA。

circuit analysis

论文"Chain of Thought Empowers Transformers to Solve Inherently Serial Problems" 将Transformer看作一定深度的复杂电路，分析其可以解决问题的复杂度。电路复杂度分析用 $TC^0$ 表示可以通过一个固定深度的电路解决的计算问题，而足够长的思维链，能将Transformer的表达能力扩展到$TC^0$之外。

论文指出，从概念上讲，CoT赋予模型执行本质上串行计算的能力，这是Transformer所缺乏的，尤其是在深度较低的情况下。并行处理可以增加填充信息，在宽度上有机会影响采样的概率分布，进而影响最后的推理效果，但是简单的并行推理会导致模型无法提供深度信息。串行处理则通过引入中间信息，加深LLM在范畴对象和态射中遍历的深度，逐步调整采样概率分布，实现更精确的推理。CoT 则提高了低深度Transformer在内在串行问题上的表达能力，让Transformer避免简单并行推理，通过串行的方式去一步步推理。

论文进一步论证，通过T步CoT，使用固定位精度和O(logn) 嵌入大小的固定深度Transformer可以解决任何可由大小为T的布尔电路解决的问题。

上图是不同嵌入大小d(n)和CoT长度T(n)的共复杂度类之间的关系图。

6.2 机器学习角度

前向传播角度

有些方法着重研究前向传播的隐状态和权重的映射上，试图通过可视化权重和隐状态来解读语言模型的内部运作。此处我们主要介绍 logit lens。logit lens的作用是通过将 LLM 的隐状态转换为词汇概率来展示模型在生成过程中的表现，这种投影有助于理解 LLM 在生成过程中逐渐构建输出的模式。

Logit Lens的思路和原理是：

语言模型在逐层为输入分配特征。那么我们可不可以观察特征是怎么逐层变化的？
既然解码新token的过程是把最终的hidden states用线性层变换一次，然后经过softmax转换为词典的概率分布。那么把LM head提前加在每个中间层上，通过将激活值先经过transformer的最终归一化层，然后与输出嵌入矩阵相乘，就可以将激活值转换为词汇表中每个词的logit。

反向传播角度

论文"Backward Lens: Projecting Language Model Gradients into the Vocabulary Space"从反向传播矩阵来理解Transformer的运作机制。

动机

反向传播是将链式法则应用于计算导数并更新深度学习网络模型权重的过程。该过程始于模型执行前向传播，生成预测$\hat y$ 后与期望目标比较，通过损失函数进行量化差异。在此之后，模型开始反向传播，逐层计算梯度。反向传播算法通过计算每一层的梯度来更新模型中的权重。这一机制不仅使模型能够学习新的信息，也为研究人员提供了解释模型行为的机会。目前，关于反向传播的梯度如何影响模型学习和知识存储的探讨仍然较为稀缺。

该研究的动机在于扩展现有的可解释性方法，尤其是将其应用于 LM 的反向传播过程，比如如何将梯度信息有效地应用于模型的知识更新与编辑中。通过分析反向传播中的梯度矩阵，研究者能够更全面地理解信息在模型中的流动。

此外，该论文还提出了一种新的思路：通过将梯度矩阵映射到词汇空间，揭示 LM 在学习新知识时的内在机制。通过这一方法，研究者希望能够明确地理解模型如何在多层次上进行信息存储和记忆。

方案

将Logit Lens应用于梯度矩阵

在分析中，研究者专注于MLP层，这是识别和编辑存储知识的重要领域。MLP模块由两个紧密连接的矩阵（$FF_1$和 $FF_2$）构成。

具体来说，$FF_1$将输入从 $R^d$映射到$R^{d_m}$ ，而 $FF_2$则将其映射回 $R^d$。由于梯度矩阵的维度高且难以全面分析，因此研究者将每个梯度矩阵的外积形式转换为一组较小的向量。每个由 $x_i^\top \cdot \delta_i$ 形成的矩阵可以同时从两个视角进行解释：一方面作为 $x_i$ 的跨度（线性组合），另一方面作为 $\delta_i$ 的跨度。研究者利用这种双重性，通过聚焦于 n 个向量的线性组合来分析梯度。此外，研究者也指出 $FF_1$的梯度使用 $x_i$作为其跨度集合， $FF_2$的梯度则使用$\delta_i$ 作为其跨度集合。通过这种分析，研究者能够更深入地理解 MLP 层中存储信息的复杂机制，也可以通过构建特定的跨度集合来提高对梯度矩阵的解释能力。

上图展示了通过$x^⊤·δ$的外积来计算梯度矩阵的过程。矩阵的每一行由相同的值组成。在图的上方，我们将矩阵描述为δ的跨度（span），而在图的下方，我们将其描述为x的跨度。矢量被转置展示以强调跨度效果。

上图展示了依据"莱昂内尔·梅西效力"的prompt，给出"巴黎"这个回答时，LM的一个 MLP 层的前向与反向传播过程，以及梯度对模型更新的影响。具体表现为梯度（以绿色表示）和权重（以蓝色表示）之间的相互作用。MLP的第一个矩阵$FF_1$试图将在前向传播过程中遇到的信息合并在模型的权重（蓝色）中。利用词汇投影（vocabulary projection）方法，论文作者发现这些信息代表了token"团队"。第二个矩阵$FF_2$的梯度则旨在将$FF_2$编码的信息向新目标的embedding 方向移动。

知识存储与模型编辑的机制

我们接下来看看如何利用反向传播中的梯度更新 MLP 层的权重。论文提出了一种称为"印记与偏移"（imprint and shift）机制的双阶段过程。该机制通过结合前向传播的输入和目标嵌入，利用梯度信息在 MLP 层中存储信息。每个 MLP 层的梯度可以表示为正向传播的输入向量和反向传播的 VJP（向量雅可比乘积）的组合。具体地，梯度在更新过程中的表现可以表示为：

\[\frac{\partial L}{\partial W} = x_i^\top \cdot \delta_i \]

在这个表达式中， $x_i$ 是前向传播的输入，而 $\delta_i$ 是相应的 VJP。当使用反向传播更新 LM 的 MLP 层时，会发生以下两个主要阶段的变化：

印记阶段：这个过程将给定输入的"印记"附加到 MLP 层。输入 $x_i$ 被加入或减去到 $FF_1$的神经元中，从而调整每个与输入对应的 $FF_1$神经元的激活程度。

偏移阶段：此阶段涉及对 $FF_2$的输出进行调整，具体表现为从 $FF_2$ 的神经元中减去 $\delta_i$，以放大在启用 VJP 值后对输出的影响。这相当于将之前概率较低的词汇提升为预测可能性更高的目标。

上图展示了反向传播的印记和偏移机制。"grad"表示梯度矩阵中的单个神经元。$FF_1$ 的grad的颜色与前向传播输入相同，而$FF_2$的梯度则与新的目标嵌入相同，这表明它们彼此相似。

6.3 生物学角度

随着神经网络的诞生及后续的辉煌发展，研究者们一直在为神经网络寻找生物学上的解释，生物学上的进展也在启发AI研究人员开发新模型。

星形胶质细胞

论文"Building transformers from neurons and astrocytes"指出，由神经元和其他称为星形胶质细胞（astrocyte ）的脑细胞组成的生物网络可以执行与 Transformer 相同的核心计算。论文从计算角度探讨了星形胶质细胞在大脑中发挥的作用，并制作了一个数学模型，展示了如何将它们与神经元一起构建一个生物学上合理的 Transformer。

动机

Transformer 会比较句子中的所有单词以生成预测，这个过程称为自注意力。为了让自注意力发挥作用，Transformer 必须以某种形式的记忆保存所有单词，但由于神经元的交流方式，这在生物学上似乎是不可能的。

然而，研究一种略有不同类型的机器学习模型（Dense Associated Memory）的科学家意识到，这种自注意机制可能发生在大脑中，但前提是至少三个神经元之间存在通信。而星形胶质细胞（不是神经元）可以与神经元形成三向连接，即所谓的三方突触。星形胶质细胞可以向神经元发出信号。因为星形胶质细胞的运作时间比神经元长得多------它们通过缓慢升高然后降低钙反应来产生信号------这些细胞可以保存并整合从神经元传递给它们的信息。通过这种方式，星形胶质细胞可以形成一种记忆缓冲区。

因此，论文作者假设星形胶质细胞可以在 Transformer 的计算方式中发挥作用。

方案

论文作者从计算角度探讨了星形胶质细胞在大脑中发挥的作用，建立了神经元-星形胶质细胞网络的数学模型，展示了如何将它们与神经元一起，构建一个生物学上合理的 Transformer，即该模型可以像 Transformer 一样运行。

上图中，A部分给出了神经元-星形胶质细胞网络的概述。Transformer块由一个前馈网络近似，该前馈网络具有一个星形胶质细胞单元，该单元覆盖了隐藏层和最后一层之间的突触（矩阵H）。B部分则展示了在写入阶段，可以使用Hebbian学习规则更新神经元之间的权重，使用突触前可塑性规则更新神经元与星形胶质细胞之间的权重。在读取阶段，星形胶质细胞在数据流经网络时会调节突触权重H。

通过分析，论文作者表明，他们的生物物理神经元-星形胶质细胞网络理论上与 Transformer 相匹配。此外，他们通过将图像和文本段落输入 Transformer 模型和模拟神经元星形胶质细胞网络，发现两者都以类似的方式回应提示，这证实了论文作者的理论模型。

海马体

论文"RELATING TRANSFORMERS TO MODELS AND NEURAL REPRESENTATIONS OF THE HIPPOCAMPAL FORMATION"则从负责记忆的海马体（Hippocampal ）角度做出了分析。

虽然Transformer模型是在完全没有生物学知识辅助的情况下开发出来的，但在数学上，Transformer的架构却和目前神经科学中的海马体模型极其相似，尤其是网格细胞（grid cell）和位置细胞（place cell）。所以基于transformer的大语言模型（比如GPT、Bard等）实际上在模仿海马及内嗅皮层处理信息的方式。采用递归位置编码的Transformer可以精确复制海马结构。

上图显示了Transformer如何准确地复制了在海马体中观察到的那些模式。

TEM（Tolman-Eichenbaum Machine）模型是一种神经科学模型，这种序列学习器可以捕捉海马体和内嗅皮层（内侧/外侧；MEC/LEC）中的许多已知神经现象。下图给出了TEM模型的结构，以及它和Transformer的对比。

该论文的研究似乎也说明了，我们的人脑中存在类似自然语言处理中常用的词向量（包含了词的语义信息）并且编码了词的位置，而且，大脑中似乎也存在一个类 transformer 模型。

6.4 数学角度

ODE视角

以微分方程的概念来审视和解释神经网络是近年来兴起的一个新的研究方向，深度神经网络（DNNs）有一个共同特征：输入数据按照顺序被逐层处理，形成一个时间离散的动态系统。基于此，研究者们假设特定类型的神经网络可以看作是离散的微分方程，所以可以使用现成的微分方程求解器来进行计算，希望可以得到效果更好且具有强解释性的结果。

神经常微分方程

论文"Neural Ordinary Differential Equations"提出了一种名为神经常微分方程的模型，这是新一类的深度神经网络。神经常微分方程不拘于对已有架构的修修补补，它完全从另外一个角度考虑如何以连续的方式借助神经网络对数据建模。

推导

目前较为常用的神经网络，例如残差网络都是通过堆叠一系列的转换块（transformations）或残差块来形成一个隐层状态以建立复杂的转换。当随着网络的层数不断加深，网络推理计算的每一步都足够小时，即接近极限时，我们对网络的隐藏层神经元的连续动态进行参数化，就可以得到对应的Neural ODE。具体推导如下图所示。我们可以将输出层定义为在某时刻上常微分方程（ODE）初值问题的解，这个值可以通过一个常微分方程求解器进行计算。

优势

其实无论是什么结构的神经网络，本质上都是在拟合一个复杂的非线性复合函数，其中复合的次数其实等价于神经网络的层数。要对网络进行求解，首先需要找到网络参数的梯度，这就涉及到链式法则，其要求在网络前向传播的过程中保留所有层的激活值，并且在反向传播的时候再利用这些激活值进行计算，这对设备内存或显存的占用非常大，因此一般情况下无法训练很深层数的网络。

而Neural ODE来可以直接通过方程求解器来计算网络梯度，但是当网络的层数较深时，计算的误差会逐渐累加，因此引入了一个伴随状态方法（Adjoint State Method）来计算ODE的梯度。该方法将网络梯度的计算转化为解一个ODE，随后可以将隐藏层状态的导数作为一个参数，这样参数就不是原本的离散序列，而是一个连续的向量场（vector field），因此就不需要前向传播去一一计算，也就不需要耗费大量空间来保存中间结果了。

综上所述，Neural ODE框架可以使用伴随状态方法在不存储激活值的情况下进行网络学习，因此显著减少了原本反向传播时的大量内存使用空间，同时也提供了一个理论框架，从ODE的连续视角来研究深度学习模型。

示例

神经常微分方程（Neural ODE）的核心操作是对网络隐藏层状态的导数进行参数化，进而建立起与隐藏层强相关的微分方程，如果可以使用某种手段直接将中间层的结果求解出来。比如，论文指出：残差网络与常微分方程（ODE）之间存在着密切的关系。具体来说，残差网络可以被看作是求解常微分方程的欧拉方法的离散化版本，即ResNets可以被视为一组特定Neural ODE的离散化。所以可以使用现成的微分方程求解器来进行计算。

上图对两种网络进行对比，可以让我们更直观地理解Neural ODE。右侧上方的残差网络定义了有限变换的离散序列。从0到1再到5的转换代表了离散的网络层，每一层都会通过一个激活函数进行非线性转换。我们可以将其中的黑色评估位置视为神经元，它会对其输入进行转换以调整传递的信息。而ODE网络则定义了一个向量场，隐藏状态在其中进行连续转换，黑色的评估点会根据预设的误差容忍度自动调整其位置。

Do Residual Neural Networks discretize Neural Ordinary Differential Equations?

论文"Do Residual Neural Networks discretize Neural Ordinary Differential Equations?"对ResNets与Neural ODEs之间的联系进行进一步的深入研究。

论文首先量化ResNets的隐藏层状态轨迹与其对应的Neural ODE的解之间的距离，随后发现使用梯度下降算法优化ResNets得到的平滑性，可以以一定的速率对Neural ODE进行正则化，并且其能达到的深度以及所需的优化时间与梯度下降算法一致。基于该发现，论文提出可以使用无记忆（memory-free）的离散邻接法（adjoint method）来训练ResNets，并表明如果残差函数与输入符合李普希茨（Lipschitz）条件，这种方法在理论上可以支持较深层ResNets的训练。最后，论文成功地用邻接法在在残差层中没有内存消耗的情况下对非常深的ResNets进行微调。

多粒子动态系统视角

论文"Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View"从多粒子动态系统（MPDS/Multi-Particle Dynamic System）的角度提出了对Transformer架构的新理解，将其在数学上解释为一种数值常微分方程（ODE）求解器。其实，这也是ODE的另一种视角。

多粒子的动态系统是在物理中常见的一种动态系统，在流体力学中通常以动态系统的常微分方程来模拟，这种动态系统的常微分方程叫做对流扩散方程（Convection-diffusion Equation）。比如粒子位置对时间的导数是两个函数的和，第一个函数是 F，这是N个粒子共同作用的一个N元函数（通常被称为Diffusion）；第二个函数是G函数，是对每个粒子单独作用的阐述（通常被称为Convection）。这与 Transformer 结构中的 MHA 与 FFN 形成了一种很自然的契合。因为MHA 考虑到句子中不同单词的语义和依赖关系，从而用这些信息来捕获句子的内在结构和表示。FFN则是独立应用于句子中每个位置的单词，对每个单词采用相同的线性变换，从而把每个位置的上下文编码到更高维度的表示。FFN是Convection的过程，多头自注意力机制就是是Diffusion的过程。因此我们可以用这种多粒子的对流扩散方程来解释 Transformer结构的含义。我们接下来看看其推导思路。

在流体力学中，单个粒子的运动会用两个部分模拟（此处对应下图标号1）：
- 一个是该粒子本身的运动，通常被称为Convection。
- 一个是是其他粒子对其作用，通常被称为Diffusion。
对于一个多粒子动态系统(Multi-Particle Dynamic System)，在流体力学中通常以如下图标号2的方程进行模拟。
用Lie-trotter法解上面的常微分方程，得到标号3。
多头自注意力机制可以用标号4的公式来表示，该公式可以演变成标号6，对应上面多粒子动态系统里的函数F。
FFN可以用标号5的公式来表示，对应多粒子动态系统里的函数G。
综合标号5和6，得到Transformer的一层为标号7。

因此，Transformer的处理流程可以看作是：tokens从一个初始位置经过一段时间的处理之后，呈现在高维度空间中的另一位置。

论文作者也指出，Lie-Trotter splitting scheme 事实上是一种早已被淘汰掉的数值解法，是一阶的近似方法。在实际中去解常微分方程的时候，人们用的都是Strang splitting。相较而言，Strang splitting 是一种比较好的数值解，是一种二阶的近似方法。因此，论文作者提出了把 Strang splitting 这种常微分方程的数值解法对应一种神经网络的话，这个网络叫做Macaron结构，具体如下图所示。

上述方法是从纯粹的数学角度出发，将 Deep Neural Networks 看作一种 Ordinary Differential Equation 的 Numerical solver。论文通过找常微分方程更好的数值解的方法，将其对应回一种更好的网络结构。这种新的 Transformer 结构的性能较之传统有了显著提升。与业界公司通过实验来探索不同，Macaron结构是在"人力"思考的基础上，用数学的方法设计出了一个更好的网络。

流映射视角

论文"A Mathematical Perspective On Transformer"尝试提供一个从数学角度研究 Transformers 通用且易于理解的框架。DNN 可以看作是从一个$\mathbb R^d$到另一个$\mathbb R^d$的流映射（Flow Map），而Transformer可以被认为是在$\mathcal P (R^d)$上的流映射，即在$\mathbb R^d$ 上的概率测度空间（the space of probability measures）的映射。为了实现这种在度量空间进行转换的流映射，Transformers 建立了一个平均场相互作用的粒子系统（mean-field interacting particle system.）。

论文的模型只关注 Transformer 架构的两个关键组成部分：自注意力机制和layer normalization。.

layer normalization有效地将粒子限制在时间变化为轴的单位球体$\mathbb{S}^{d-1}$的空间内部。
自注意力机制是通过经验度量实现粒子之间的非线性耦合（the particular nonlinear coupling of the particles done through the empirical measure）。或者说，自注意力机制是互相作用的粒子系统中的非线性耦合机制（nonlinear coupling mechanism）。

完整的Transformer被表示如下图所示。

论文还为自注意机制引入了一个更简单好用的替代模型，一个能量函数的 Wasserstein 梯度流，而能量函数在球面上点的最优配置已经有成熟的研究方法。

差分角度

Transformer结构容易往往会过度关注不相关的上下文，从而倾向于将attention权重分配给这些无关的上下文中。其原因是，随着上下文变长，微小的不相关token的注意力之和可能超过对少数相关token的注意力，从而淹没它们。随着输入长度的增加，经典Transformer可能越来越难以捕捉到关键信息。

论文"Differentical Transformer"的作者称这些无关的上下文为注意力噪音（attention noise）。因此，论文作者为了解决注意力噪音问题，提出了DIFF Transformer。具体来说，「差分注意力」（differential attention）将注意力分数计算为两个单独的softmax 注意力图之间的差异，从而通过减法消除了噪声。这样可以能放大对答案范围的注意力并消除噪音，促使模型关注上下文中的关键信息，从而增强上下文建模的能力。

总体架构

为了方便说明，论文使用了仅解码器（decoder-only）模型作为示例来描述该架构。模型的整体架构和传统Transformer 布局一致，整个模型由L个DIFF Transformer层堆叠而成，每层由一个差分注意力模块和前馈网络模块连接形成。给定一个输入序列 x，模型将输入嵌入打包成 $X^0$，此后输入会被进一步逐层处理，最终获得输出$ X^L$。

相比于 Transformer，差分 Transformer 的主要差别在于使用差分注意力替换了传统的 softmax 注意力，同时保持整体宏观布局不变。此外，论文也参考 LLaMA 采用了 pre-RMSNorm 和 SwiGLU 这两项改进措施。其中 $W^G$、$W_1$、$W_2 $是可学习的矩阵。

Differential Attention（差分注意力）

「差分注意力」是指两个softmax函数间的差异来消除注意力噪声。这个想法类似于电气工程中提出的差分放大器，将两个信号之间的差来消除输入的共模噪声。此外，降噪耳机的设计也基于类似的想法。

差分注意力机制具体如下：

给定输入 X，首先将它们投射成查询、键和值 $Q_1$、$Q_2$、$K_1$、$K_2$、$V$。对应下图标号1。
将query和key 向量分为两组，并计算两个单独的softmax注意力，然后将这两个softmax的差值作为最终注意力分数。对应下图标号2。

可以通过 λ 的大小动态的控制两个注意图之间的权衡程度，从而更好的适用不同的输入和任务要求。

多头

DIFF Transformer中也可以使用多头注意力机制。令 h 表示注意力头的数量。该方法对各个头使用不同的投影矩阵 $W^Q_i 、W^K_i 、W^V_i ，i ∈ [1, h]$。标量 λ 在同一层内的头之间共享。然后通过拼接各个头的输出并进行投影获得最终结果。

下图给出了多头差异注意力机制和代码示例。其中使用了 GroupNorm (・) 来强调 LN (・) 独立应用于每个 head。由于差分注意力往往具有更稀疏的模式，因此头之间的统计信息更加多样化。为了改进梯度的统计情况，LN (・) 算子会在连接操作之前对每个头进行归一化。

下面给出了具体代码。地址：https://github.com/microsoft/unilm/tree/master/Diff-Transformer

python 复制代码

class MultiheadDiffAttn(nn.Module):
    def __init__(
        self,
        args,
        embed_dim,
        depth,
        num_heads,
    ):
        super().__init__()
        self.args = args
        self.embed_dim = embed_dim
        
        # arg num_heads set to half of Transformer's num_heads
        self.num_heads = num_heads
        
        # arg decoder_kv_attention_heads set to half of Transformer's num_kv_heads if use GQA
        # set to same as num_heads if use normal MHA
        self.num_kv_heads = args.decoder_kv_attention_heads if args.decoder_kv_attention_heads is not None else num_heads
        self.n_rep = self.num_heads // self.num_kv_heads
        
        self.head_dim = embed_dim // num_heads // 2
        self.scaling = self.head_dim ** -0.5
        
        self.q_proj = nn.Linear(embed_dim, embed_dim, bias=False)
        self.k_proj = nn.Linear(embed_dim, embed_dim // self.n_rep, bias=False)
        self.v_proj = nn.Linear(embed_dim, embed_dim // self.n_rep, bias=False)
        self.out_proj = nn.Linear(embed_dim, embed_dim, bias=False)

        self.lambda_init = lambda_init_fn(depth)
        self.lambda_q1 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0,std=0.1))
        self.lambda_k1 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0,std=0.1))
        self.lambda_q2 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0,std=0.1))
        self.lambda_k2 = nn.Parameter(torch.zeros(self.head_dim, dtype=torch.float32).normal_(mean=0,std=0.1))

        self.subln = RMSNorm(2 * self.head_dim, eps=1e-5, elementwise_affine=True)
    
    def forward(
        self,
        x,
        rel_pos,
        attn_mask=None,
    ):
        bsz, tgt_len, embed_dim = x.size()
        src_len = tgt_len

        q = self.q_proj(x)
        k = self.k_proj(x)
        v = self.v_proj(x)

        q = q.view(bsz, tgt_len, 2 * self.num_heads, self.head_dim)
        k = k.view(bsz, src_len, 2 * self.num_kv_heads, self.head_dim)
        v = v.view(bsz, src_len, self.num_kv_heads, 2 * self.head_dim)

        q = apply_rotary_emb(q, *rel_pos, interleaved=True)
        k = apply_rotary_emb(k, *rel_pos, interleaved=True)

        offset = src_len - tgt_len
        q = q.transpose(1, 2)
        k = repeat_kv(k.transpose(1, 2), self.n_rep)
        v = repeat_kv(v.transpose(1, 2), self.n_rep)
        q *= self.scaling
        attn_weights = torch.matmul(q, k.transpose(-1, -2))
        if attn_mask is None:
            attn_mask = torch.triu(
                torch.zeros([tgt_len, src_len])
                .float()
                .fill_(float("-inf"))
                .type_as(attn_weights),
                1 + offset,
            )
        attn_weights = torch.nan_to_num(attn_weights)
        attn_weights += attn_mask   
        attn_weights = F.softmax(attn_weights, dim=-1, dtype=torch.float32).type_as(
            attn_weights
        )

        lambda_1 = torch.exp(torch.sum(self.lambda_q1 * self.lambda_k1, dim=-1).float()).type_as(q)
        lambda_2 = torch.exp(torch.sum(self.lambda_q2 * self.lambda_k2, dim=-1).float()).type_as(q)
        lambda_full = lambda_1 - lambda_2 + self.lambda_init
        attn_weights = attn_weights.view(bsz, self.num_heads, 2, tgt_len, src_len)
        attn_weights = attn_weights[:, :, 0] - lambda_full * attn_weights[:, :, 1]
        
        attn = torch.matmul(attn_weights, v)
        attn = self.subln(attn)
        attn = attn * (1 - self.lambda_init)
        attn = attn.transpose(1, 2).reshape(bsz, tgt_len, self.num_heads * 2 * self.head_dim)

        attn = self.out_proj(attn)
        return attn

图灵完备性质

论文"ASK , AND IT SHALL BE GIVEN: TURING COMPLETE - NESS OF PROMPTING"首次从理论层面证明了大语言模型(LLM)中的prompt机制具有图灵完备性。

图灵完备性（Turing Completeness）是计算理论中的一个核心概念，用来描述某个计算系统的计算能力。如果一个系统具备条件分支、循环或递归能力，并具有理论上的无限存储，那么它可以被称为图灵完备。只要给它足够的时间和资源，这种系统能够模拟任意其他可计算的计算机，执行任何可编程的任务。具备这些特征的系统可以用来模拟任何其他图灵完备的系统。因此，图灵完备的系统之间是等价的，理论上可以用来模拟任何其他图灵完备的系统。图灵机被认为是所有可计算过程的最终抽象，在传统计算理论中，图灵机用于衡量其他系统的计算能力。

当我们说LLM的提示是图灵完备的，意味着我们可以将LLM视为一个通用计算器，只需通过精心设计的prompt，一个固定大小的Transformer模型理论上可以计算任何可计算函数，能够完成任何可以编程的任务。更重要的是，这个固定大小的模型在计算复杂度上几乎可以达到所有不限大小的Transformer模型的理论上限。这为我们使用LLM解决复杂问题提供了一个全新的视角，也为prompt工程提供了坚实的理论基础。

论文在理论和技术层面上的主要贡献是：

表达能力：展示了提示的图灵完备性。研究者证明，存在一个固定大小的Transformer Γ，对于任何可计算函数 φ，存在一个相应的有限提示$π_φ$，使得对于任意输入 x，Transformer Γ 在提示$π_φ$ 的指导下能够计算出 φ(x) 的结果。重要的是，构造的 Transformer Γ 与具体的函数 φ 无关，提示$π_φ$ 与输入 x 也无关，且输入 x 可以是任意长度。
链式思维（CoT）复杂性：研究表明，构造的 Transformer Γ 可以在 $O(t(n))$ 步内计算任何$ TIME_2(t(n)) $类函数，并可以在 \$O(t(n) log t(n))\$ 步内计算任何$ TIME(t(n)) $类函数，即使是对于长度为 n 的输入。值得注意的是，单个 Transformer 也可以达到几乎与所有 Transformer 类相同的 CoT 复杂性。
精度复杂性：研究还展示了构造的 Transformer Γ 可以在$ O(log(n + t(n)))$ 位精度内计算任何 $TIME(t(n))$ 类函数。这意味着，即使是单个 Transformer 也能够达到与所有 Transformer 类相同的精度复杂性。

论文揭示了Prompt的真正潜力：通过合适的设计，我们可以让Transformer模型执行任何复杂的计算任务。对于Prompt工程师来说，提示不再只是给定模型的一段简单文本，而可以将提示看作一种编程语言，通过合适的语法和结构来表达复杂的逻辑和操作。这意味着在设计提示时，我们不仅可以关注如何让模型理解任务，更可以从计算理论的角度出发，去设计能够高效完成计算的提示。只要提示设计得足够巧妙，它就可以模拟任意计算过程，这让Prompt工程具备了更深层次的科学基础。

范畴论

Symbolica首席科学家Paul 在2024年六月份发表了一篇文章想要通过范畴论来统一描述和研究深度学习架构。

范畴学是一种研究数学结构和它们之间关系的数学分支。它关注于对象和态射之间的映射关系，以及这些映射关系之间的组合和复合规则。范畴学提供了一种统一的语言，可以描述和比较不同数学结构之间的共性和相似性，从而使得数学家能够在不同领域之间建立联系和发现共性。在进行类比时，范畴学能够帮助我们发现不同数学领域之间的类似性，找到它们之间的共同模式和结构。通过将问题抽象成范畴论的语言，我们可以将原本复杂的问题简化为更一般性的形式，从而更容易进行类比和推理。范畴学的一些基本概念，如对象、态射、同态和自然变换等，可以帮助我们在不同数学领域之间建立桥梁。这种概念的应用可以使得类比更加灵活和高效，从而促进对问题的深入理解和解决。因此，范畴学是数学中进行类比的一个非常有效的工具，它使得数学家和研究者能够在广泛的数学领域中发现新的见解和联系。同时，范畴学也在其他领域，如计算机科学、物理学和哲学等方面得到了广泛的应用。

如果将深度学习模型视为范畴，则深度学习模型的层可以被视为范畴中的对象，层之间的数据流和变换可以被视为态射。在深度学习中，单子可以用来描述模型必须满足的约束，例如对称性或等变性，代数可以用来描述模型的参数和前向传播。单子代数同态可以用来描述模型层之间的转换，例如从一个层的输出到另一个层的输入。这样使用范畴论来构建和分析深度学习模型，可以帮助实现模型的可信性。比如：

范畴论提供了一种清晰的方式来描述模型的组件和它们之间的相互作用，这有助于理解模型的工作原理。
通过单子来定义模型必须满足的约束，如等变性和对称性，确保模型的行为符合预期。
可以对模型的属性进行形式化验证，确保它们满足特定的数学和逻辑规则。

范畴视角下的transformer，就是"通过预训练找到每层组合分段线性函数"，并参数化。

大语言模型之所以能够很好地回答问题，部分原因在于其训练数据中包含了各种范畴的信息，并且通过学习这些范畴，模型可以在回答问题时进行类比和推理。在训练大语言模型时，通常会使用大规模的语料库，其中包含了丰富的语言和知识。这些语料涵盖了各种主题、领域和概念，使得模型能够从中学习到大量的范畴和相关信息。当模型接收到一个问题时，它可以尝试从已经学到的范畴中找到类似的类比，然后将问题映射到类似的问题上，进而给出答案。这种类比和推理的过程是通过模型内部的神经网络层次结构和权重参数实现的。

6.4 物理学角度

获得玻尔兹曼奖的物理学家霍菲尔德也曾在一次访谈中提到，"如果你不能用数学的语言去描述大脑，那你将永远不知道大脑是怎么工作的"。而鉴于他自身的习惯，"如果一个问题和我熟知的物理毫无联系，那我将无法取得任何的进展"。所以，在人工智能正在重塑人类社会方方面面的同时，我们有必要去了解物理学的思想如何影响人们对神经网络乃至自我的认知。

数据相当于一种初始化，可以驱动网络连接权重的连续更新以获得一个聪明的自适应的物理模型，而这个更新过程是端对端地优化一个目标函数，优化的过程即执行在高维空间的朗之万动力学。神经网络的奥秘正是在于高维的权重空间，它本质上服从正则系综分布。半严格的物理分析给出了权重空间的分布和数据驱动的权重的对称性破缺。从物理直观出发，人们可以获取非平衡神经动力学的稳态全貌以及隐藏的动力学相变；甚至，人们可以将大语言模型的示例泛化归结为两体自旋模型，依此可以洞察智能的本质。

基本动力学特性

论文"THE ASYMPTOTIC BEHAVIOR OF ATTENTION IN TRANSFORMERS"通过严格的数学分析，揭示了Transformer中注意力机制的基本动力学特性。ASYMPTOTIC （渐近特性）研究的是当某一系统或者函数趋于无穷大或某一特定值时，系统或者函数的性质如何变化。

论文的研究表明，在多种条件下，所有token都会渐近地趋于收敛，收敛行为可能导致模型崩溃，限制输出的多样性。这一发现不仅深化了我们对Transformer模型的理解，也为改进模型设计提供了重要理论指导。未来的研究可以基于此来进一步探索更复杂的模型动力学，并开发更有效的注意力机制变体。

主要定理与证明

定理3.2：单头情况下，当注意力矩阵为时不变、正定和对称时，系统动力学表现为黎曼梯度向量场。
定理4.1：当token的初始位置位于椭球某个半球的内部时，系统会收敛到共识平衡点。
定理5.1：在自回归情况下，对于几乎所有初始条件，系统都会收敛到由第一个token决定的共识状态。
定理6.1：在符合一定假设条件下（比如U是对称的），如果所有令牌都从其中一个半球开始，则令牌将收敛到共识均衡点（此外，该均衡是渐近稳定的）。

下图给出了连续模型（ continuous model ）的几个特定情况下的结果，其中Q(t)、K(t)和U(t)分别表示查询矩阵、键矩阵和值矩阵。

下图展示了定理3.2。在下图左侧，我们可以看到10个token在由随机生成的正定对称矩阵定义的椭球体上的运动。正如预期的那样，所有token都收敛到共识均衡。在这种情况下，动力学是一个梯度向量场。图右侧则显示了相应电势（corresponding potential）的时间演化。

下图展示了定理4.1。在图的左侧展示了10个token在球体上的运动。我们可以看到所有token开始都并保持在一个半球中，它们最终收敛到共识均衡。其时间演化如图右侧所示。

下图展示了定理6.1。在图的左侧，我们可以观察到token收敛到共识平衡点，而在右侧给出了对应的时间演化。

物理自旋系统的结构

博客"Transformers Are Secretly Collectives of Spin Systems"认为Transformer模块的神经网络架构蓝图可以从经典统计力学中熟悉的物理自旋系统的结构中导出。更具体地说，博客作者认为Transformer模块的正反向传播可映射为矢量自旋模型中的计算磁化。进而可以将Transformer想象成可微自旋系统的集合，其行为可以通过训练来塑造。

训练一个深度transformer模型，相当于通过建立一个可微的关联结构来编排一堆transformer模块，其中一个自旋系统的磁化驱动下一个自旋系统。训练过程中的摆动(数十亿)参数会推动自旋系统集合的级联反应行为，以更好地适应由数据和损失函数指定的集合(元)任务。

受力角度

也有研究人员认为，transformer机制本质上是描述一个运动轨迹，attention是message passing，其实就是计算受力，MLP可以看作是计算在受力作用下的按照运动方程的运动轨迹，transformer优化的过程，就是通过数据训练来寻求作用力和运动方程从而达到构造满足要求的运动轨迹的过程。

0x07 总结

我们首先给出LLaMA的架构，这是Transformer应用的经典案例。在其推理过程中，每 step 内，输入一个 token序列，经过Embedding层将输入token序列变为一个三维张量[b, s, h]，经过一系列计算，最后经logits层将计算结果映射至词表空间，输出张量维度为[b, s, vocab_size]。

Transformer的处理流程就是token流转的过程：token从从一个初始位置经过一段时间在高维度空间中的另一位置，这是从一个语义空间迁移到了另一个语义空间的过程，或者说，token是常微分方程在不同时间、不同维度的表示。在这个过程中，Attention、FFN和esNet 缺一不可但却各司其职，Attention做信息的提取和聚合，Resnet 提供信息带宽，而真正学到的知识或者信息大多存储在 FFN 中。其具体特点如下：

一个句子进来，它首先被离散化成一个个单词token的集合，然后 Q，K，V就像是指针一样，将这些单词实体映射到背后的概念，实现实体的识别和概念的绑定
transformer中的encoder与RNN中的encoder作用一样，都是做输入序列各个时间步信息的特征抽取。
- Y: <-- LayerNorm(Y + Masked-MultiHead(Y))相当于RNN中各个时间步的 $ℎ_{t−1}$ 和$ y_t $。
  
  m_Y=MultiHead(X, Y)相当于RNN中关联encoder与decoder的注意力context计算。
  
  Y = LayerNorm(Y + m_Y)相当于context与RNN单元各个时间步的 $ℎ_{t−1}$ 和$ y_t $的拼接。
而 $Attention(Q,K,V) = softmax( \frac{QK^T}{\sqrt d_k} ) \times V$ 则通过累加和乘积的形式，实现概念和概念的一个全连接图，它代表了所有可能的命题结构（主谓宾），并最终得到新的一组可能的命题结构，
接下来通过后面的全连接层（类似一个命题结构的词典），得到新的命题（句子）。
通过层数的增加， transformer可以组合得到从简单到复杂逻辑的嵌套结构，也就是实现全文级别的推理。

7.1 效果

Transformer论文从三个维度比较了当时特征提取的主流框架。这三个维度分别为：每一层的计算复杂度、串行操作的复杂度、最大路径长度。

我们可以从这三个指标分别探讨。

首先看序列操作的复杂度。这是自注意力机制的唯一弱点。当序列长度 n 比较大的时候，时间复杂度较高。而大模型时代对长文本的诉求，使这个弱点愈发凸显。目前也有很多方法来解决这个问题。
其次看串行操作的复杂度。自注意力机制的复杂度是O(1)，表示一步就可以完成，并行度最高。RNN 则为 n，因为每一个计算都依赖前面的结果，所以需要 n 步才能完成，也就是无法并行。循环层最大的问题是不能并行训练，序列计算复杂度是O(n)。而自注意力层和卷积一样可以完全并行。
最后看看最大路径长度，其表示数据从某个位置传递到另一个位置的最大长度。注意力本来就是全局查询操作，任意两个位置之间都可以直接联系，可以在O(1)的时间里完成所有元素间信息的传递。它的信息传递速度远胜卷积层和循环层；CNN 是 $log_{k} n$；而 RNN 最坏情况下，开始位置和结束位置的距离为 n.

7.2 优劣

除了上面分析的优点之外，Transformer还有其他优点，比如：

模型可解释性比较高（不同单词之间的相关性有多大）。Self-Attention模型更可解释，Attention结果的分布表明了该模型学习到了一些语法和语义信息。RNN由于其内部复杂的状态更新，往往被认为是一种"黑箱"模型，很难理解内部的决策过程。与此相对，Attention机制提供了一种直观的方式来可视化和理解模型是如何关注序列中不同部分的。通过分析注意力权重，我们可以清楚地看到模型在做出预测时，哪些输入元素起到了关键作用。

高度适应性：Transformer的架构包含了堆叠的编解码器，这种设计使其不仅在自然语言处理领域，在计算机视觉和语音识别等多个领域也能发挥出色的适应性。

Transformer的缺点也同样明显，比如：

自注意力机制本身具有二次复杂度，这种复杂度使得该架构在涉及长输入序列或资源受限情况下计算成本高昂且占用内存巨大。
位置编码本身就是一个妥协之举。词向量保存了词语的语言学信息（词性、语义）。然而，位置编码在语义空间中并不具有这种可变换性，它相当于人为设计的一种索引。那么，将这种位置编码与词向量相加，就是不合理的，所以不能很好地表征位置信息。
局部信息的获取不如RNN和CNN强。
参数阈值的牢笼。大模型由于参数量大，往往存在大量的冗余参数，这些参数在训练过程中可能并没有学习到有效的信息，反而增加了模型的复杂性和训练的难度。大量的参数还会导致模型发生过拟合问题。参数过多的另一个副作用就是模型无法学习到更高层级的有效特征：由于存在大量的冗余参数，模型可能无法有效地学习到更高层级的特征。这可能会限制模型的性能，尤其是在处理复杂任务时。大型模型的巨量参数还会导致模型的优化过程更为困难，梯度下降等优化算法在大型模型上可能会遇到局部最优、梯度消失或梯度爆炸等问题。

正因为Transformer存在的各种问题，研究者们正在寻找各种方法来进行优化，并提高模型的泛化能力和解释性。比如：

很多研究者正在探索知识蒸馏、模型剪枝、参数共享等技术来减少模型的参数量，以降低计算资源的消耗，提高训练效率。
很多研究者在对Transformer架构进行改进：注意力模块稀疏化，在注意力中引入记忆信息，对外部记忆（kv对）的注意力运算，线性随机注意力，在Transformer中引入递归，线性注意力（performer）。
很多非 Transformer 研究都循着"保留 RNN 优势的同时，试图达到 Transformer 性能"的方向去努力。

0xFF 参考

[interpreting GPT: the logit lens](https://www.lesswrong.com/posts/AcKRB8wDpdaN6v6ru/interpreting-gpt-the-logit-lens) nostalgebraist
A Mathematical Framework for Transformer Circuits (Anthropic blog 2021)
A Mathematical Perspective On Transformers
A PRIMER ON THE INNER WORKINGS OF TRANSFORMER-BASED LANGUAGE MODELS
Analyzing Transformers in Embedding Space
ASK, AND IT SHALL BE GIVEN: TURING COMPLETENESS OF PROMPTING
Backward Lens: Projecting Language Model Gradients into the Vocabulary Space
Chain of Thought Empowers Transformers to Solve Inherently Serial Problems
Differential Transformer

](https://arxiv.org/pdf/2410.05258)
DIFFERENTIAL TRANSFORMER
EMNLP 2024最佳论文：从反向传播矩阵来理解Transformer的运作机制 PaperWeekly
Finding Neurons in a Haystack: Case Studies with Sparse
Four types of emergence: a typology of complexity and its implications for a science of management
Full Stack Transformer Inference Optimization Season 2: Deploying Long-Context Models)Yao Fu | Website | Blog | Twitter / X
GPT4技术原理五：大模型的幻觉，解铃还须系铃人王庆法清熙
 Grothendieck Graph Neural Networks Framework: An Algebraic Platform for Crafting Topology-Aware GNNs
Jawahar, Ganesh, et al. "What Does BERT Learn about the Structure of Language?" ACL 2019
Let's Think Dot by Dot: Hidden Computation in Transformer Language Models
LLM CoT的工作原理王庆法清熙
 LLM的Prompt竟然是图灵完备的？LLM提示范式的第一个研究 | 重磅 AI修猫Prompt
MetaFormer is Actually What You Need for Vision
More About Attention 李新春
 Neural Ordinary Differential Equations
nGPT: Normalized Transformer with Representation Learning on the Hypersphere
Reformer 模型 - 突破语言建模的极限 Hugging Face 博客
 softmax is not enough
State-Free Inference of State-Space Models:The Transfer Function Approach
THE ASYMPTOTIC BEHAVIOR OF ATTENTION IN TRANSFORMERS
The Platonic Representation Hypothesis
TRANSFORMER EXPLAINER: Interactive Learning of Text-Generative Models
transformer 模型结构详解及实现 zhang
Transformers Are Secretly Collectives of Spin Systems mcbal
Transformer在生物学上是否合理？MIT团队用神经元和星形胶质细胞来构建 ScienceAI 药物分子设计
 Transformer模型‌(上篇) OnlyInfo
Transformer模型‌(下篇) OnlyInfo
Transformer的物理原理 Matthias Bal 清熙
 Understanding and Improving Transformer From a Multi-Particle Dynamic System Point of View
Understanding how LLM inference works with llama.cpp omrimallis
Wavelets based physics informed neural networks to solve non-linear differential equations
【官方双语】直观解释注意力机制，Transformer的核心 | 【深度学习第6章】 3Blue1Brown
万字长文介绍为大语言模型建立的"语言、统计和范畴"数学框架 Tai-Danae Bradley 编译：王庆法
大脑里也有个Transformer！和「海马体」机制相同人工智能与算法学习
 大语言模型背后的神经科学机制雅牧
 打开黑匣子的神器来了！Transformer Explainer让Transformer模型透明化小智智驻未来
 探索AGI系列 | 番外01. （全新视角理解）Transformer和大脑新皮质的一致性 MetaUniTech
智源论坛 | 王立威：从经验性的积累到理论空白的弥补北京智源人工智能研究院
 浅谈LLM mechanistic interpretability的几个流派（一）时间旅客
 理解llama.cpp怎么完成大模型推理的 hugulas
神经网络理论研究的物理学思想黄海平 [现代物理知识杂志]
范畴的相变与知识的形成
 解读小模型------SLM 半吊子全栈工匠喔家ArchiSelf
论文阅读：Differentical Transformer 差分Transformer Eddie
降低大模型幻觉的必由之路清熙
 https://poloclub.github.io/transformer-explainer