2.1 语言模型

2.1.1 语言是可计算的

第一章里面我们讲了语言的分析要素。很多东西其实还是传统语言学里面的定义，只不过我们通过一些案例比如CRF、文法等内容给大家展示了语言是可以被数学建模的。那么，这种低层级的语法解析是如何与高等级的对话式大模型联系起来的呢？这种层级的数学建模显然不能让机器充分理解语言的语义和知识。

想一想每次在使用deepseek-r1的时候，它生成回答总是一个光标顺序地向后生成字符。虽然现在这个光标移动的方式已经被证明是个纯纯的特效了，但是在早期，文本生成模型真的就是这样工作的。这种工作模式被称作"Next-Word Prediction"。比如，你问一句："How are you?"，我立马知道要丝滑三连"I'm fine, thank you, and you?"，对不？对于机器来讲，这个操作是怎样的呢？

首先它为了响应are和you，我在第一个词里面得用I'm(I am)来响应，这把第一个词定下来了。
I am是主语+be动词，那么系表结构，后面跟什么词的可能性最大呢？比如我们如果给不同词性的词分配概率，be动词在这里后面跟着概率最高的是形容词，然后概率排名第二的可能是什么动词ing、被动语态什么玩意，这其实就是一个概率分布。而如果我们把视角进一步缩小到具体的词汇，就发现fine这个单词的概率又是所有单词里面最高的，好那我们就选它，第二个词定了。
上文生成了I'm fine, 下一个词会生成什么还是直接到句号呢？我们发现在语料库当中，很多英文课文都不会直接一句I'm fine结束对话，很多课文都是在后面都跟着thank you是吧？很好，你学英语的课文作为训练语料已经开始影响你的语言概率分布了，跟着第三个单词是thank的概率就比跟句号的概率更大。
同理，上文已经生成了I'm fine, thank后面肯定接you嘛，这个概率肯定最大，然后同理继续生成。
上文生成了I'm fine, thank you, 接下来第五个单词就也是根据课本习惯的概率分布，跟着and的概率就比结束对话的概率大一点点，虽然有不少课文确实是在这里结束对话的，但后面跟了and you的课文篇数比结束对话的课文还是多一些，因此概率分布上后面更有可能接下句。
上文I'm fine, thank you, and，后面接点什么呢？当然是you最大了。
上文I'm fine, thank you, and you后面我们发现语言、语法、语义都完整了，这个时候预测概率最大的next word是个句号，我们把句号补上，终止生成。

这就是一个对话系统生成文本时的生成原理。通过这个例子，我们发现，不管是早期的文本生成系统还是现在的大语言模型，本质上，这都是个next-word prediction任务。

如果我们用数学化形式化的语言描述这个事情，它的本质就是建模一个序列的最大化概率：

\[\arg\max P(S)=P(w_1w_2\cdots w_n) \]

从上面的案例我们也可以看得出来，每个词的生成其实受到上文的影响，换而言之，第n个词受到前n-1个词的影响；第n-1个词的取值受到前n-2个词的影响......一直到开头。如果用数学形式表达，这事实上是个条件概率：

\[\begin{align} \arg\max P(S)&=P(w_1w_2\cdots w_n)\\ &=P(w_n|w_1w_2\cdots w_{n-1})P(w_1w_2\cdots w_{n-1})\\ &=P(w_n|w_1w_2\cdots w_{n-1})P(w_{n-1}|w_1w_2\cdots w_{n-2})P(w_1w_2\cdots w_{n-2})\\ &=\cdots\\ &=\prod_{i=2}^n P(w_i|w_1w_2\cdots w_{i-1}) \times P(w_1) \end{align} \arg\max P(S)=P(w_1w_2\cdots w_n) \]

这里，概率是通过训练语料来处理、学习从而得到的。没错，这就是语言建模的核心------概率分布。通过这个例子，我们发现：每个词的取值影响下一个词，然后语义信息是序列化影响，这很像一个随机过程。现在我可以告诉大家，不是像，就是！语言是一个可稳态遍历的随机过程。而这个next-word prediction，也是现在交互式大语言模型训练的根本原理，我们后面会看到。

语言模型的分布是受到语料影响的。打个简单的比方，当有人问你"How are you"，你会下意识地回答"I'm fine, thank you, and you?"，但是你要拿这个问题问老外他们绝对不会这么说。能说出这套丝滑小连招的只有我们国人，因为我们小学英语课本是这样写的。你看，这就是一个概率分布的问题，由于这种回答在我们一直学习的英语课本里面被反复提及因此概率印象在我们的脑壳里面被加强了，但是老外可能给的是另外的回答，所以这一联合分布的概率值往往没有他们语境下的回答概率大。

那对于机器而言，怎么获得这个概率值呢？

2.1.2 N-Grams语言模型

早期的语言模型，在机器学习还没诞生以前，是通过词典法用频率估计概率得到的语义分布。N-Grams就是早期语言模型的代表性方法。
定义：N-Gram模型是一种基于统计的语言模型，其核心思想是通过前文连续的n-1个词（即上下文窗口）来预测当前词的概率。数学上，一个N-Gram模型假设第k个词的概率仅依赖于前n-1个词，即满足马尔可夫假设。

数学表达 ：

对于词序列 $ w_1, w_2, ..., w_k $，其联合概率可分解为：

\[P(w_1, w_2, ..., w_k) = \prod_{i=1}^k P(w_i | w_{i-n+1}, ..., w_{i-1}) \]

以Bigram（n=2）为例，每个词仅依赖前一个词：

\[\begin{align*} P(w_1, w_2, ..., w_k)&=\prod_{i=1}^k P(w_i | w_{i-n+1}, ..., w_{i-1})\\ &=\prod_{i=1}^k P(w_i | w_{i-1}) \end{align*} \]

\[P(w_i | w_{i-1}) = \frac{\text{Count}(w_{i-1}, w_i)}{\text{Count}(w_{i-1})} \]

说白了，这不就是一个词频统计的问题吗？概率是通过数频数得到的。

2. 基于词频统计的Next-Word概率估计（以Bigram为例）

既然如此，我们构造一个词典。比如，如果我们训练语料是莎士比亚全集，我们把里面所有的单词获取出来给个编号。假设莎士比亚大全集里面有N个单词，我们创建一个N*N的矩阵，矩阵的每一行每一列表示某个单词。矩阵A[i,j]表示两个先后出现的单词word[i],word[j]在文章当中出现的频次，比如"you are"这两个单词经常在一起出现，频率就会比较高。给它记录成表格，后面推断条件概率的时候就用的上了。

步骤：

构建语料库 ：收集文本并分词，如 ["人工智能", "是", "未来", "的", "技术"]。
统计Bigram频率 ：遍历文本，记录相邻词对出现的次数，如 ("人工智能", "是") 出现3次。
计算条件概率 ：

\[P(w_i | w_{i-1}) = \frac{\text{Count}(w_{i-1}, w_i)}{\text{Count}(w_{i-1})} \]

示例：

若语料中 "人工智能" 出现10次，其后续词 "技术" 出现6次，则概率为：

\[P(\text{技术} | \text{人工智能}) = \frac{6}{10} = 0.6 \]

可能这里有同学会说：老师，语料里面如果有上百万个单词，那么这个词表百万乘以百万可就是百亿级别的大矩阵了！一台PC真的能存储和计算这么大的矩阵吗？当然是不行的！不管是分布式系统还是别的什么玩意效率都低了，因此这种方法在小语料上还能管用，一到大规模语料库就废了。大家反思一下是什么原因引起的？对了，就是矩阵里面0太多了！我们把这种现象称作稀疏（sparse），因为很多词汇他根本构不成搭配凑不起来！比如(big,small)你见过他俩会凑一块的么？那显然不会啊。至于说这种稀疏表示还有没有更好的优化方案，使得单台PC就可以估算概率，肯定是有的，我们放在下一节再说。

3. Python代码实现（Bigram模型）

python 复制代码

from collections import defaultdict

class BigramModel:
    def __init__(self):
        self.bigram_counts = defaultdict(lambda: defaultdict(int))
        self.vocab = set()

    def train(self, corpus):
        for sentence in corpus:
            tokens = sentence.split()
            for i in range(len(tokens)-1):
                prev, curr = tokens[i], tokens[i+1]
                self.bigram_counts[prev][curr] += 1
                self.vocab.update([prev, curr])

    def predict_prob(self, prev_word, curr_word):
        total = sum(self.bigram_counts[prev_word].values())
        return (self.bigram_counts[prev_word][curr_word] + 1) / (total + len(self.vocab))  # 加一平滑

# 示例
corpus = ["人工智能 是 未来 技术", "技术 推动 人工智能 发展"]
model = BigramModel()
model.train(corpus)
print(model.predict_prob("人工智能", "是"))  # 输出：0.333...

4. 数据平滑技术

目的：解决未登录词（OOV）或低频N-Gram导致的零概率问题。未登录词其实就是语料里面没出现但是在应用到新任务的时候出现了，比如莎士比亚全集里面没有登革热这个词，结果我们用在莎士比亚全集上训练的语言模型应用到一个鬼医学数据库的文本生成上的时候，很有可能出现这种情况。
常用方法：

加一平滑（Laplace） ：所有N-Gram计数加1，公式：

\[P(w_i | w_{i-1}) = \frac{\text{Count}(w_{i-1}, w_i) + 1}{\text{Count}(w_{i-1}) + |V|} \]
Good-Turing估计：用低频N-Gram的频率修正高频概率。
Katz回退（Backoff）：若高阶N-Gram不存在，回退到低阶模型。
插值平滑 ：加权组合不同阶N-Gram概率，如：

\[P_{\text{interp}}(w_i|w_{i-1}) = \lambda P(w_i|w_{i-1}) + (1-\lambda) P(w_i) \]

5. N-Gram在NLP中的应用

文本生成：基于历史词预测后续词（如聊天机器人）。当然那都是上世纪古董用的方法了。
拼写纠错：根据上下文概率修正错误输入。这个，在早期的语法纠正系统（GEC）里面，用的还是比较多的，当然后来也都深度学习了。
语音识别：从候选序列中选择概率最高的文本。
机器翻译：评估译文的流畅性。通过语言联合建模的方式，分析从源语言到目标语言的变换后，目标语言译文的全局联合概率是否足够大，用这种联合概率的方式评估语言模型流畅程度。
信息检索：通过词共现改进搜索相关性。这种方法在早期文本检索系统有着重大意义，尤其是以前还在搞布尔检索的时代（上世纪七八十年代的古董），那会儿把统计语言模型引进来不知道方便了多少搜索引擎。

6. N-Gram模型的局限性

数据稀疏性：高阶N-Gram需要海量数据，长尾词对难以覆盖。
局部依赖限制：仅建模短距离上下文，无法捕捉长程语义（如段落主题）。
语义模糊性：无法理解同义词或抽象概念（如"苹果"指水果还是公司）。
维度爆炸 ：当n≥4时，参数量随$|V|^n$增长，存储和计算成本剧增。

2.2 神经语言模型

2.2.1 神经网络与深度学习

我们似乎总在提机器学习和深度学习。究竟什么是深度学习？那就不得不提神经网络这个玩意了。神经网络本质上是为了模仿人脑神经元连接结构而设计的一种数学模型，比如说，一个逻辑回归模型：

\[y=\frac{1}{1+e^{-(w_1x_1+w_2x_2+b)}} \]

它是不是能画成这种图的形式：

好，如果我现在组合多个输出呢？

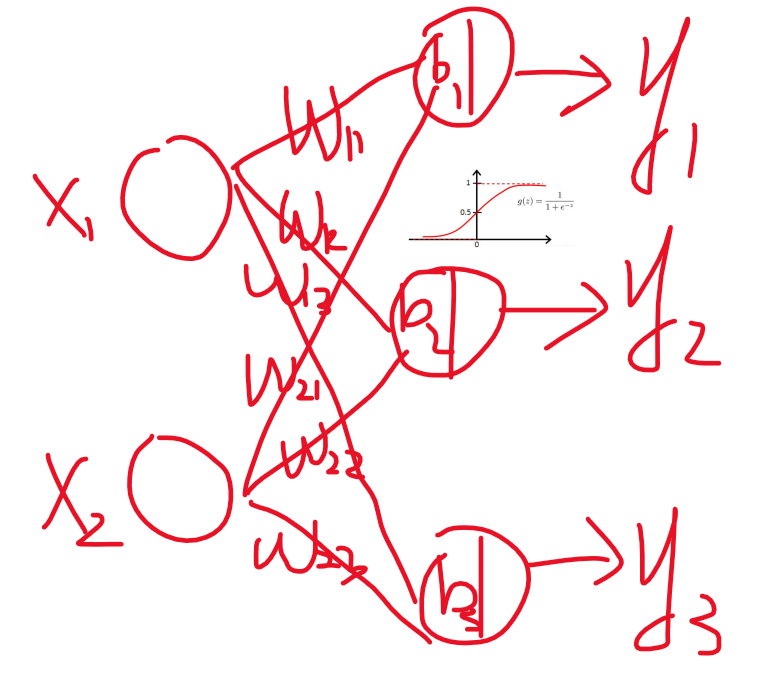
比如说我如果要做一个鸢尾花数据集的三分类，这就可以直接做，这就形成了感知机模型。那我如果把多个感知机堆起来会怎么样？（方便起见，我后面权重就用矩阵W和偏置向量b来表示了）：

That's right，这就是多层感知机，也叫人工神经网络。节点就是神经元，边就是神经末梢和突触，边上有权重，神经元上有偏置项和激活函数。这就是神经网络的基本结构。当然，还可以继续加深。

深度前馈网络（Deep Feedforward Network，DFN）是一种典型的人工神经网络结构，其核心特征在于信息的单向流动------从输入层经若干隐藏层最终传递至输出层，网络中没有循环或反馈连接。前馈计算过程可描述为逐层非线性变换的叠加：输入数据首先通过输入层接收，随后每一层的神经元对前一层的输出进行线性加权求和（权重矩阵与输入向量的乘积加上偏置项），再通过激活函数（如ReLU、Sigmoid）引入非线性，将结果传递给下一层。例如，对于第l层的神经元，其输出可表示为：

\[\mathbf{h}^{(l)} = \sigma\left( \mathbf{W}^{(l)} \mathbf{h}^{(l-1)} + \mathbf{b}^{(l)} \right) \]

其中$\sigma$为激活函数，$\mathbf{W}^{(l)}$和$\mathbf{b}^{(l)}$分别为该层的权重和偏置。最终，输出层通过Softmax函数（分类任务）或线性变换（回归任务）给出预测结果。这一过程本质上是将原始输入通过多层抽象特征映射，逐步逼近复杂的输入-输出关系。

基本思想：反向传播（Backpropagation）是神经网络训练的核心算法，其目标是通过梯度下降优化网络参数（权重和偏置），使预测结果与真实标签的误差最小化。其核心思想是利用链式法则（Chain Rule）从输出层反向逐层计算损失函数对各参数的梯度，进而更新参数。

基本流程：

前向传播：输入样本通过网络逐层计算，得到预测输出。
损失计算：通过损失函数（如交叉熵、均方误差）量化预测值与真实值的误差。
反向传播：从输出层开始，计算损失对每层参数的梯度，逐层传递误差信号。
参数更新：利用梯度下降法（如SGD、Adam）沿梯度负方向调整参数，减小损失。

数学推导 ：

以均方误差损失$\mathcal{L} = \frac{1}{2}(y - \hat{y})^2$为例，假设第$ l $层的激活函数为Sigmoid，则：

输出层误差项：

\[\delta^{(L)} = (y - \hat{y}) \cdot \sigma'(z^{(L)}) \]
反向传播至隐藏层：

\[\delta^{(l)} = \left( \mathbf{W}^{(l+1)} \delta^{(l+1)} \right) \odot \sigma'(z^{(l)}) \]
参数梯度：

\[\frac{\partial \mathcal{L}}{\partial \mathbf{W}^{(l)}} = \delta^{(l)} \mathbf{h}^{(l-1)\top}, \quad \frac{\partial \mathcal{L}}{\partial \mathbf{b}^{(l)}} = \delta^{(l)} \]

通过迭代更新$\mathbf{W}^{(l)} \leftarrow \mathbf{W}^{(l)} - \eta \frac{\partial \mathcal{L}}{\partial \mathbf{W}^{(l)}} $，网络逐步收敛至最优参数。

传统N-Gram语言模型依赖局部词频统计，存在数据稀疏性和长距离依赖建模能力不足的缺陷。神经网络语言模型（Neural Language Model，NLM）通过分布式表示（词嵌入）和深层结构突破了这些限制：

词嵌入：将词映射为稠密向量（如Word2Vec），捕捉语义相似性（如"猫"与"犬"向量相近）。
上下文建模：循环神经网络（RNN）或Transformer可建模任意长度的上下文信息，例如LSTM通过门控机制捕捉长距离依赖。
概率预测 ：以"基于上下文的词概率预测"为目标，如给定前文序列$w_{1:t-1}$，输出$P(w_t|w_{1:t-1})$的分布。

2.2.2 前馈神经网络作为语言模型

神经网络可以被应用到语言模型中来。比如我们如果还是和N-Gram一样的模式，我们把每个词在词典中的编号记作一个0-1向量（独热编码），把上N个词作为输入、下一个词作为输出来训练，能不能行？当然能。把上N个词和下N个词作为输入预测中间的目标词，能不能行，当然也能得行。这就是两种NLM建模基本范式：Next-Word Prediction 和Mask Language Modeling的基本思想。

下面是从我实验报告抄的。。。

实战：训练一个前馈神经网络作为语言模型

需要的包主要是pytorch，没有环境的同学请自行配置。

处理语料，编写DataSet类。这里前馈神经网络我们保持和n-grams一样的配置。

python 复制代码

import torch
import torch.utils.data as Data
from collections import Counter
import pickle
import numpy as np
import jieba

class Dataset():
    def load(self, obj_file):
        with open(obj_file, 'rb') as f:
            data_loaded = pickle.loads(f.read())
            self.vocab_size = data_loaded.vocab_size
            self.n = data_loaded.n
            self.batch_size = data_loaded.batch_size
            self.top_words = data_loaded.top_words
            self.train_dataset = data_loaded.train_dataset
            self.test_dataset = data_loaded.test_dataset
            self.train_dataloader = data_loaded.train_dataloader
            self.test_dataloader = data_loaded.test_dataloader

    def save(self, obj_file):
        with open(obj_file, 'wb') as f:
            str = pickle.dumps(self)
            f.write(str)

    def gen(self, vocab_size, n, batch_size=512, filename='dataset.txt', encoding="utf-8", type="n_gram"):
        self.vocab_size = vocab_size
        self.n = n
        self.batch_size = batch_size

        with open(filename, encoding=encoding) as f:
            # used to select the top common words
            words = f.read().split()
        with open(filename, encoding=encoding) as f:
            # used to construct n-gram
            lines = f.readlines()
        def clean_text(text):
            text = text.strip()
            text = ' '.join(text.split())
            return text
        def segment_sentences(text):
            return list(jieba.cut(text))

        # 对清洗后的每行文本进行分词
        cleaned_lines = [clean_text(line) for line in lines]
        segmented_lines = [segment_sentences(line) for line in cleaned_lines]

        # count the number of occurrences of each word
        # 构建词汇表
        all_words = [word for sentence in segmented_lines for word in sentence]
        word_counts = Counter(all_words)

        # print word_counts to file according to the frequency of occurrence
        with open('word_counts.txt', 'w') as f:
            for word, count in word_counts.most_common():
                f.write(word + ' ' + str(count) + '\n')

        # top words
        self.top_words = {word[0]:idx+1 for idx, word in enumerate(word_counts.most_common(vocab_size-1))}
        print("top words:", self.top_words)
        
        x = []
        y = []
            
        if type=="n_gram":
            # n-gram
            for line in lines:
                words = line.split()
                if len(words) >= n:
                    for i in range(len(words)-n+1):
                        x.append([self.top_words.get(word, 0) for word in words[i:i+n-1]])
                        y.append(self.top_words.get(words[i+n-1], 0))
        elif type=="rnn":
            # for rnn
            for line in lines:
                words = line.split()
                if len(words) >= n:
                    for i in range(len(words)-n+1):
                        x.append([self.top_words.get(word, 0) for word in words[i:i+n-1]])
                        y.append([self.top_words.get(word, 0) for word in words[i+1:i+n]])
        else:
            assert False, "Unknown Type"
        
        print("x shape:", np.array(x).shape)
        print("y shape:", np.array(y).shape)

        # split the data set into training set and test set
        dataset = Data.TensorDataset(torch.tensor(x), torch.tensor(y))
        test_size = 1000
        train_size = len(dataset)-1000
        self.train_dataset, self.test_dataset = Data.random_split(dataset, [train_size, test_size])
        self.train_dataloader = Data.DataLoader(self.train_dataset, batch_size=batch_size, shuffle=True)
        self.test_dataloader = Data.DataLoader(self.test_dataset, batch_size=batch_size, shuffle=True)
        print("train batch count:", len(self.train_dataloader))
        print("test batch count:", len(self.test_dataloader))

编写FNN的模型架构，保存到NN.py文件中。

python 复制代码

import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F
    
class FNN(nn.Module):
    def __init__(self, vocab_size, input_size, embedding_dim, hidden_size):
        super().__init__() # 这个函数定义模型中用到的各个层
        self.embedding = nn.Embedding(vocab_size, embedding_dim)
        self.norm = nn.LayerNorm(embedding_dim, elementwise_affine=False)
        self.flatten = nn.Flatten()
        self.linear_relu_stack = nn.Sequential(
            nn.Linear(input_size, hidden_size),
            nn.ReLU(),
            nn.Linear(hidden_size, embedding_dim),
            nn.ReLU()
        )
        
    def forward(self, x): # 这里写各个层之间的连接方式
        x = self.embedding(x) # 把单词进行独热编码形成embedding嵌入向量
        x = self.norm(x)	# 归一化，数据预处理
        x = self.flatten(x)	# 展平，方便后续线性层处理
        x = self.linear_relu_stack(x)	# 二层的前馈网络，采用ReLU激活函数
        x = torch.matmul(x, self.embedding.weight.T)	# 得到词向量矩阵weight，通过矩阵乘法形成语言模型。
        return x

class Trainer():
    def __init__(self, learning_rate, model):	# 一些超参数调节以及GPU配置，如果电脑上有显卡、装了显卡驱动就可以用起来会快一些
        self.loss_fn = nn.CrossEntropyLoss()
        self.optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
        self.device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
        self.model = model.to(self.device)

    def train(self, dataloader, model=None, loss_fn=None, learning_rate=None):
        if model is None:
            model = self.model
        if loss_fn is None:
            loss_fn = self.loss_fn
        if learning_rate is None:
            optimizer = self.optimizer
        else:
            optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)

        size = len(dataloader.dataset)
        model.train()
        for batch, (X, y) in enumerate(dataloader):	# 训练框架在这里
            X, y = X.to(self.device), y.to(self.device)	# 启动GPU

            # Compute prediction error
            pred = model(X)	# 计算结果
            # 计算误差
            loss = loss_fn(pred.reshape(-1,pred.shape[-1]), y.flatten())

            # Backpropagation，反向传播
            optimizer.zero_grad()
            loss.backward()
            optimizer.step()

            if (batch+1) % 100 == 0:
                loss, current = loss.item(), (batch + 1) * len(X)
                print(f"loss: {loss:>7f}  [{current:>5d}/{size:>5d}]")

    def test(self, dataloader, model=None, loss_fn=None):
        if model is None:
            model = self.model
        if loss_fn is None:
            loss_fn = self.loss_fn
        
        size = len(dataloader.dataset)
        num_batches = len(dataloader)
        model.eval()
        test_loss, correct = 0, 0
        with torch.no_grad():	# 测试模式
            for X, y in dataloader:
                X, y = X.to(self.device), y.to(self.device)
                pred = model(X)
                test_loss += loss_fn(pred.reshape(-1,pred.shape[-1]), y.flatten()).item()
                # print(np.prod(pred.shape[:-1]))
                correct += (pred.argmax(-1) == y).type(torch.float).sum().item()*pred.shape[0]/np.prod(pred.shape[:-1])
        test_loss /= num_batches
        correct /= size
        print(f"Test: \n Accuracy: {(100*correct):>0.1f}%, Avg loss: {test_loss:>8f} \n")
        return correct, test_loss

开始加载数据集、预处理并训练

python 复制代码

import torch
import torch.nn as nn
import torch.utils.data as Data
import numpy as np
import random
from collections import Counter
import os
import matplotlib.pyplot as plt
import importlib

# custom import
import dataset
import NNv2 as NN
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
print("device: " + str(device))

# parameters
vocab_size = 1024
embedding_dim = 16
n = 9
input_size = embedding_dim * (n-1)
hidden_size = 64

learning_rate = 1e-3
batch_size = 512

# model
importlib.reload(NN)

model = NN.FNN(vocab_size, input_size, embedding_dim, hidden_size).to(device)
print(model)
# prepare data
importlib.reload(dataset)

data = dataset.Dataset()
if os.path.exists("data_n_gram.pkl"):
    data.load("data_n_gram.pkl")
else:
    data.gen(vocab_size=vocab_size, n=n, batch_size=batch_size, filename='dataset.txt', encoding="utf-8", type="n_gram")
    data.save("data_n_gram.pkl")

# prepare trainer
if cumulative_epoch is None:
    cumulative_epoch = 0
x_record = []
y_record = []

trainer = NN.Trainer(learning_rate, model)
# train
epochs = 20
learning_rate = 1e-3
for t in range(epochs):
    print(f"Epoch {cumulative_epoch+1}\n-------------------------------")
    trainer.train(data.train_dataloader, learning_rate=learning_rate)
    correct, test_loss = trainer.test(data.test_dataloader)

    cumulative_epoch+=1
    x_record.append(cumulative_epoch)
    y_record.append((correct, test_loss, learning_rate))
    
    if cumulative_epoch % 5 == 0:
        if not os.path.exists('checkpoint'):
            os.makedirs('checkpoint')
        torch.save(trainer.model.state_dict(), './checkpoint/FNN-'+str(cumulative_epoch)+'.pth')
print("Done!")

得到的训练困惑度曲线如图所示：

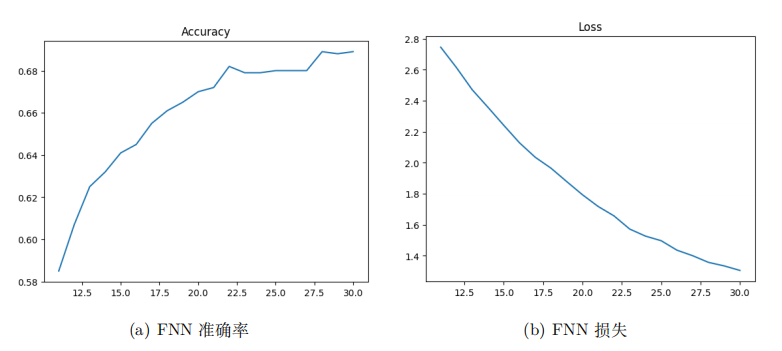
评估语言模型及困惑度

首先给定一个词，看看神经网络认为next word怎么样：

python 复制代码

def get_lookup_table(model):
    lookup_table = model.embedding.weight.data
    lookup_table = lookup_table.cpu().numpy()
    return lookup_table

lookup_table = get_lookup_table(trainer.model)
print(lookup_table.shape)

def top_10_similar(lookup_table, word_idx):
    word_vec = lookup_table[word_idx]
    similarity = np.dot(lookup_table, word_vec)/np.linalg.norm(lookup_table, axis=1)/np.linalg.norm(word_vec)
    a = np.argsort(-similarity)
    for i in a[:10]:
        name_list = [key for key,value in data.top_words.items() if value==i]
        if len(name_list) > 0:
            print(name_list[0], similarity[i])
        else:
            print("<UNK>", similarity[i])

word = random.choice(list(data.top_words.keys()))
word = "这"
print(word)
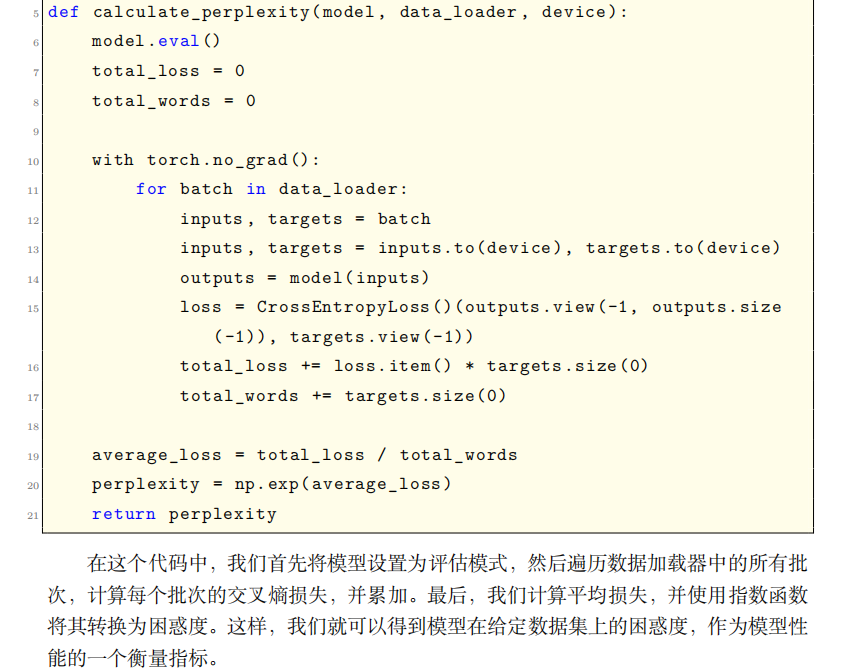
top_10_similar(get_lookup_table(trainer.model), data.top_words[word])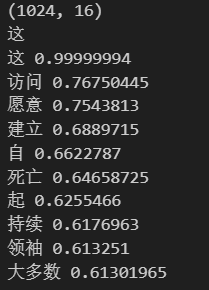

对于困惑度评估：

2.2.3 循环神经网络作为语言模型

1. 循环神经网络的基本原理与训练

基本原理

循环神经网络（Recurrent Neural Network, RNN）是一种专为处理序列数据设计的神经网络结构。与传统前馈神经网络不同，RNN通过引入"循环连接"使网络具备记忆能力，能够捕捉序列中时间步之间的动态依赖关系。其核心思想是：在每个时间步$t$，网络接收当前输入$\mathbf{x}t$和前一时刻的隐藏状态$\mathbf{h}{t-1}$，通过参数共享机制（同一组权重矩阵反复使用）计算当前隐藏状态$\mathbf{h}_t$，并输出预测结果$\mathbf{y}_t$。数学表达为：

\[\mathbf{h}t = \sigma(\mathbf{W}{hh} \mathbf{h}{t-1} + \mathbf{W}{xh} \mathbf{x}_t + \mathbf{b}_h) \]

\[\mathbf{y}t = \mathbf{W}{hy} \mathbf{h}_t + \mathbf{b}_y \]

其中，$\sigma$为激活函数（如Tanh），$\mathbf{W}{hh}$、$\mathbf{W}{xh}$、$\mathbf{W}_{hy}$为权重矩阵，$\mathbf{b}_h$、$\mathbf{b}_y$为偏置项。RNN的循环特性使其能够建模任意长度的序列，例如文本、语音或时间序列数据。

训练方法

RNN的训练基于时间反向传播算法（Backpropagation Through Time, BPTT），其本质是将循环网络展开为时间步相连的前馈网络，再通过链式法则计算梯度。具体流程如下：

前向传播：按时间步依次计算隐藏状态和输出，直至序列末端。
损失计算 ：累加所有时间步的损失（如交叉熵损失），例如总损失$\mathcal{L} = \sum_{t=1}^T \mathcal{L}_t$。
反向传播：从序列末端开始，沿时间轴反向逐层计算损失对参数的梯度，需考虑每个时间步对当前梯度的贡献。
参数更新：利用梯度下降法调整权重和偏置，使损失最小化。

挑战与改进

RNN训练面临梯度消失/爆炸问题：长序列中梯度因多次连乘而指数级衰减或增长，导致难以捕捉长程依赖。后续改进模型（如LSTM、GRU）通过门控机制缓解此问题。

2. LSTM的设计思想、改进点与数学原理

设计思想

长短期记忆网络（Long Short-Term Memory, LSTM）是RNN的一种变体，旨在解决梯度消失问题并增强对长程依赖的建模能力。其核心改进在于引入门控机制（Gating Mechanism） 和细胞状态（Cell State） ，通过精细化控制信息的遗忘、存储与输出，实现长期记忆的稳定传递。

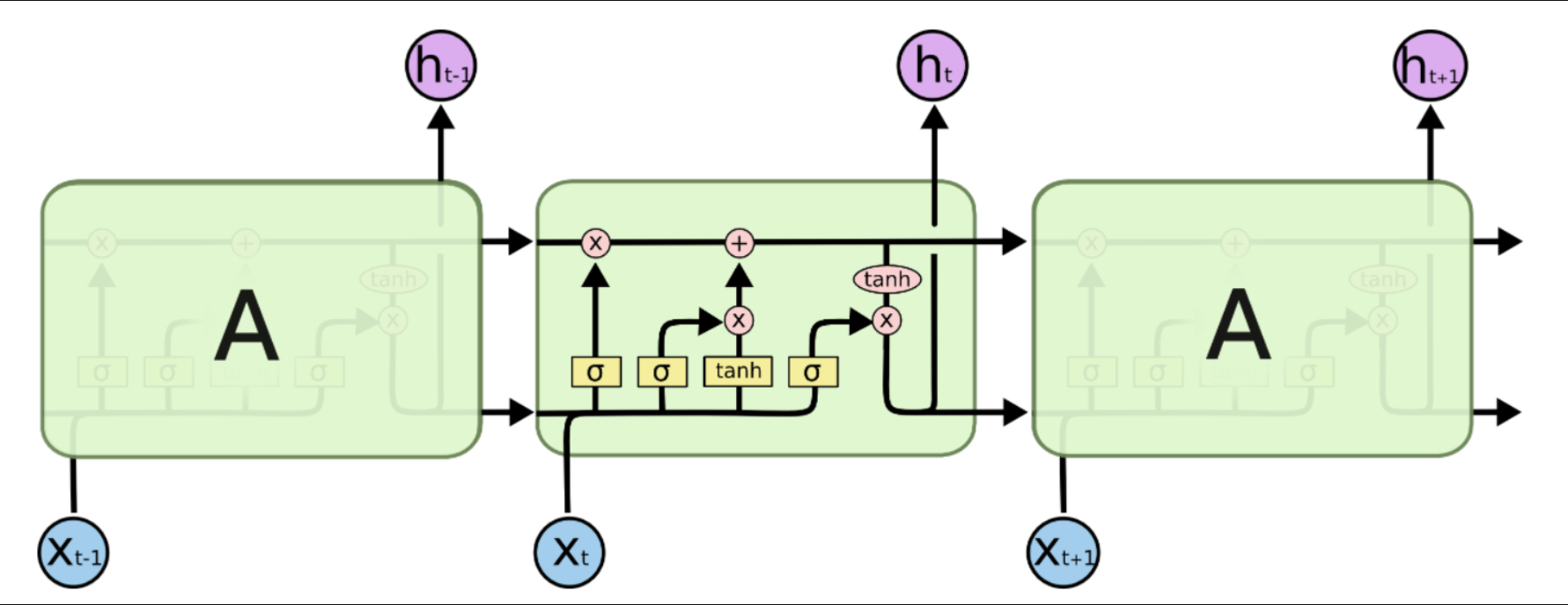
改进点

细胞状态 ：新增与隐藏状态并行的"细胞状态"$\mathbf{C}_t$，作为信息传输的主干道，仅通过线性操作（加法）传递，减少梯度衰减。
门控单元 ：
- 遗忘门（Forget Gate） ：决定前一细胞状态$\mathbf{C}_{t-1}$中哪些信息应被丢弃。
- 输入门（Input Gate） ：控制当前输入$\mathbf{x}_t$中哪些新信息应存入细胞状态。
- 输出门（Output Gate） ：基于细胞状态生成当前隐藏状态$\mathbf{h}_t$。

数学原理

优势与应用

LSTM通过门控机制动态调节信息流，有效缓解梯度消失问题，使其在机器翻译、语音识别、文本生成等任务中表现卓越，成为处理长序列数据的经典模型。后续变体（如GRU）通过简化结构进一步优化计算效率。

代码写起来其实差不多，大家可以把FNN换成LSTM再试试。因为LSTM本身对于序列信息的上下文理解和把握会比FNN更深刻一些，所以更适合在文本上进行建模。

python 复制代码

class LSTM(nn.Module):
    def __init__(self, vocab_size, input_size, embedding_dim, hidden_size):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, embedding_dim)
        self.norm = nn.LayerNorm(embedding_dim, elementwise_affine=False)
        self.lstm = nn.LSTM(input_size, hidden_size, batch_first=True)
        self.linear_relu = nn.Sequential(
            nn.Linear(hidden_size, embedding_dim),
            nn.ReLU()
        )
        
    def forward(self, x):
        x = self.embedding(x)
        x = self.norm(x)
        x, _ = self.lstm(x)
        x = self.linear_relu(x)
        x = torch.matmul(x, self.embedding.weight.T)
        return x

2.3 词向量模型

2.3.1 词向量是语言模型的副产物

在上一节当中我们通过一个简单的案例训练了神经语言模型。在神经语言模型当中我们有一个Embedding层，叫嵌入层。在嵌入之初我们是用独热的方法进行编码，而在训练过程中这个嵌入矩阵也会不断被迭代，形成一个独一无二的副产物------词向量。

我们回到N-Grams的缺点上来：用每个词在词典中的编号来表示我们说太过稀疏，非零项太少了。了解过机器学习的同学或许会知道，如果没有学习过机器学习但学习过线性代数的同学应该也了解，对高维度向量数据的降维可以通过矩阵分解等方法实现（例如PCA等），但计算量复杂。所以，我们通过神经网络形成了稀疏文本数据的稠密表示------在词向量当中，非零项占了绝大部分。并且，用向量的形式表达词汇还有一个好处：向量的位置和运算是能够反映到语义关系的。

词向量（Word Embedding）是自然语言处理中将词汇映射到低维连续向量空间的技术。与传统独热编码（One-Hot Encoding）相比，词向量通过稠密向量表示词汇的语义特征。例如，在训练良好的词向量空间中，"猫"和"狗"的向量距离较近，而"猫"与"飞机"的向量距离较远。这种分布式表征使计算机能够通过数值运算捕捉语义关系。

向量运算的语义意义

距离与相似度

词向量的相似性可通过欧氏距离或余弦相似度衡量。余弦相似度计算两向量夹角的余弦值，其公式为：

\[\text{similarity} = \frac{\mathbf{A} \cdot \mathbf{B}}{\|\mathbf{A}\| \|\mathbf{B}\|} \]

该指标对向量长度不敏感，更关注方向一致性，适合衡量语义相似性。
线性运算与语义关系

词向量的线性运算可反映语义组合规律。例如：

\[\text{vec("国王")} - \text{vec("男性")} + \text{vec("女性")} \approx \text{vec("女王")} \]

此类现象表明，词向量空间可能隐式编码了语义类比关系，但需注意此类特性在复杂语境中的局限性。

实践示例

以下代码使用预训练词向量模型实现语义计算（需提前安装gensim库）：

python 复制代码

from gensim.models import KeyedVectors
from gensim import utils

# 加载预训练词向量（需下载Google News模型）
model_path = 'GoogleNews-vectors-negative300.bin'
model = KeyedVectors.load_word2vec_format(model_path, binary=True)

# 计算余弦相似度
similarity = model.similarity('cat', 'dog')
print(f"猫与狗的相似度: {similarity:.3f}")

# 寻找类比关系
result = model.most_similar(positive=['woman', 'king'], negative=['man'], topn=1)
print(f"国王 - 男性 + 女性 ≈ {result[0][0]}")

# 计算欧氏距离
distance = model.distance('apple', 'microsoft')
print(f"苹果与微软的欧氏距离: {distance:.2f}")

自然语言处理意义

词向量将离散符号转化为连续数学表示，使得计算机能通过向量运算处理语义问题。基于此的技术包括：

文本相似度计算
语义检索与推荐
词义消歧
机器翻译中的跨语言映射

2.3.2 word2vec词向量模型

一、提出动机与范式突破

Word2Vec（Mikolov et al., 2013）的提出解决了传统前馈神经网络（FNN）词向量训练的瓶颈问题。相较于基于FNN的语言模型（如Bengio 2003年模型），其核心创新在于：

结构简化

取消隐藏层，直接通过输入层到输出层的投影计算，将参数复杂度从 (O(N^2)) 降为 (O(Nd))（N为词表大小，d为向量维度），使百万级词汇训练成为可能。
目标重构

放弃直接预测词概率，改为学习词向量本身。通过局部上下文窗口采样，模型专注于捕捉词与上下文的共现模式，而非全局概率分布。
训练优化

引入负采样（Negative Sampling）和层次Softmax（Hierarchical Softmax）技术，将输出层计算复杂度从 (O(N)) 降至 (O(\log N))，大幅提升训练速度。

注意：word2vec不是一种模型，是两种模型的一个统称。

二、模型架构原理

Word2Vec包含两种互补的建模视角：

CBOW（连续词袋模型）
- 目标：通过上下文词预测中心词
- 过程：
  1. 将窗口内上下文词的向量求平均（或加权求和）
  2. 投影到输出层计算中心词概率
  \[P(w_t | w_{t-k},...,w_{t+k}) = \text{Softmax}(\mathbf{W} \cdot \bar{\mathbf{v}}_{\text{context}}) \]
- 特点：适合高频词训练，对小规模语料鲁棒性强
Skip-Gram（跳字模型）
- 目标：通过中心词预测上下文词
- 过程：
  1. 将中心词向量直接作为投影层输出
  2. 对窗口内每个上下文位置独立计算概率
  \[P(w_{t+j} | w_t) = \text{Softmax}(\mathbf{W} \cdot \mathbf{v}_{w_t}) \]
- 特点：擅长捕捉低频词语义，更适应大规模语料

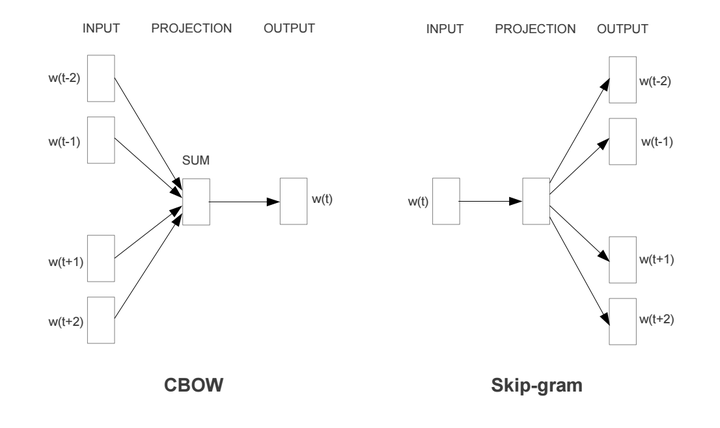
三、实践：基于Gensim的自定义训练

以下代码演示如何从原始文本训练Word2Vec模型：

python 复制代码

from gensim.models import Word2Vec
from gensim.utils import simple_preprocess

# 示例语料
corpus = [
    "word2vec captures semantic relationships between words",
    "neural networks learn distributed representations",
    "deep learning models require large datasets"
]

# 文本预处理：分词与小写化
processed_corpus = [simple_preprocess(sent) for sent in corpus]

# 模型训练
model = Word2Vec(
    sentences=processed_corpus,  # 输入语料
    vector_size=100,    # 向量维度
    window=5,           # 上下文窗口
    min_count=1,        # 最小词频
    sg=1,               # 1=Skip-Gram, 0=CBOW
    negative=5,         # 负采样数
    workers=4           # 并行线程
)

# 查看词向量
print("'semantic'的向量表示:\n", model.wv['semantic'])

# 计算相似度
similarity = model.wv.similarity('word2vec', 'models')
print(f"\n'word2vec'与'models'余弦相似度: {similarity:.3f}")

# 寻找类比关系
analogy = model.wv.most_similar(positive=['deep', 'learning'], negative=[], topn=3)
print("\n'deep learning'关联词:", analogy)

关键参数说明：

vector_size：词向量维度（通常100-300）
window：考虑前后各n个词作为上下文
sg：模型选择开关
negative：负采样数量（5-20适合小语料）
alpha：初始学习率（默认0.025）

四、模型特性分析

上下文无关性：每个词仅对应单一向量，无法处理多义词
窗口限制：仅捕获局部共现模式，缺乏长距离依赖建模
效率优势：在单机CPU上可处理十亿级token的语料

最佳实践建议：

预处理时保留短语（如"new_york"）可提升语义粒度

使用min_count=5~10过滤低频噪声词

多次迭代训练（epochs=5~10）时需降低学习率（alpha=0.01）

Word2Vec通过巧妙的工程简化，使词向量技术首次具备工业级应用价值。虽然后续的GloVe、FastText等模型在理论完备性上有所提升，但其"局部上下文预测+分布式表示"的核心思想仍深刻影响着现代词表示方法的发展。

2.4 Attention is All You Need

2.4.1 注意力机制

《Attention is All You Need》这篇文章在17年发表，是现在大语言模型的始祖起源。它的核心在于提出了两点创新------自注意力机制和Transformer模型。

首先我们聊聊什么是注意力机制：当你记一个人的面相的时候，你不是全局在观察，而是通过一些主要特征。比如你们记住我的长相，就知道：小眼睛大脑袋大脸盘子。这是因为你们的注意力放在了这些特征上。那么对于文本领域的理解呢？其实是一个样的道理。在做英语阅读题的时候，某个题目的答案最终定位只会在某个段落的某一个到某两个句子上；而判断一个选项正确与否，只需关注核心几个词或者短语的信息（命名实体、情感、事件链等）。那么这一部分信息在解决机器阅读理解（MRC）或者问答系统（QA）的过程中就有着更重要的信息，理应分配更高的注意力。

在传统神经网络中，每个神经元对所有输入信号进行固定权重的连接，如同人类在阅读时对所有文字平均分配注意力，这显然不符合认知规律。自注意力机制（Self-Attention）的突破性在于：它赋予模型动态调整关注焦点的能力，就像学生在课堂上根据知识重要性自动调整笔记详略。当处理"那只站在树枝上的鸟唱出了美妙的旋律"这句话时，模型会自动建立"鸟-树枝"的空间关系，强化"鸟-唱-旋律"的动作链条，这正是理解语义的关键。

自注意力机制的本质是通过三个核心矩阵------查询（Query）、键（Key）、值（Value）构建动态权重。给定输入序列的嵌入表示矩阵$\mathbf{X} \in \mathbb{R}^{n \times d}$（n为序列长度，d为特征维度），通过线性变换生成三个矩阵：

\[\mathbf{Q} = \mathbf{X}\mathbf{W}^Q, \quad \mathbf{K} = \mathbf{X}\mathbf{W}^K, \quad \mathbf{V} = \mathbf{X}\mathbf{W}^V \]

其中$\mathbf{W}^Q, \mathbf{W}^K, \mathbf{W}^V \in \mathbb{R}^{d \times d_k}$为可学习参数矩阵。注意力权重通过查询与键的交互计算：

\[\text{Attention}(\mathbf{Q}, \mathbf{K}, \mathbf{V}) = \text{softmax}\left( \frac{\mathbf{Q}\mathbf{K}^T}{\sqrt{d_k}} \right)\mathbf{V} \]

这里的分母$\sqrt{d_k}$用于缩放点积结果，防止梯度消失。softmax函数将分数转换为概率分布，最终输出是值的加权求和。整个过程如同信息检索系统：查询（目标词）通过键（索引系统）找到最相关的值（知识库内容）。

以下代码展示自注意力机制的完整实现过程：

python 复制代码

import torch
import torch.nn.functional as F

def self_attention(inputs, d_k):
    """
    inputs: 输入张量 [batch_size, seq_len, d_model]
    d_k: 键/查询的维度
    """
    batch_size, seq_len, d_model = inputs.size()
    
    # 生成Q,K,V矩阵
    Q = torch.nn.Linear(d_model, d_k)(inputs)  # [batch, seq, d_k]
    K = torch.nn.Linear(d_model, d_k)(inputs)  # [batch, seq, d_k]
    V = torch.nn.Linear(d_model, d_k)(inputs)  # [batch, seq, d_k]
    
    # 计算注意力分数
    scores = torch.matmul(Q, K.transpose(-2, -1)) / (d_k ** 0.5)  # [batch, seq, seq]
    
    # 注意力权重归一化
    attn_weights = F.softmax(scores, dim=-1)  # [batch, seq, seq]
    
    # 加权求和
    output = torch.matmul(attn_weights, V)  # [batch, seq, d_k]
    return output

# 示例输入（batch_size=2, seq_len=3, d_model=4）
inputs = torch.tensor([[[0.1, 0.2, 0.3, 0.4], 
                       [0.5, 0.6, 0.7, 0.8], 
                       [0.9, 1.0, 1.1, 1.2]],
                      
                      [[0.3, 0.4, 0.5, 0.6], 
                       [0.7, 0.8, 0.9, 1.0], 
                       [1.1, 1.2, 1.3, 1.4]]])

output = self_attention(inputs, d_k=4)
print("输出张量维度:", output.shape)  # torch.Size([2, 3, 4])

自注意力机制通过动态权重打破了序列处理的顺序限制。在机器翻译任务中，当处理英文句子"The animal didn't cross the street because it was too tired"时，模型会自动强化"it"与"animal"的关联，而弱化"it"与"street"的联系。这种能力在以下场景中尤为重要：

长距离依赖建模：在科技文献中，"量子纠缠"概念可能相隔多个段落与"超导电路"产生联系，自注意力能直接建立远距离关联
多模态交互：在视觉问答任务中，模型需要同时关注图像中的斑马条纹和问题中的"黑白相间"关键词
层次特征提取：处理法律文书时，先定位"违约责任"等核心条款，再分析具体赔偿细则

自注意力机制的并行计算特性（所有位置关系可同时计算）使其相比RNN更适应现代硬件加速，但其计算复杂度随序列长度呈平方级增长的问题也催生了稀疏注意力等改进方法。这一机制的成功应用不仅推动了Transformer架构的诞生，更深刻改变了我们对序列建模的认知方式------从机械的时序处理转向语义空间的动态关系构建。

2.4.2 Transformer模型

Transformer架构的提出（Vaswani et al., 2017）标志着序列建模从循环神经网络（RNN）的时序驱动范式转向了全局关联的并行化范式。传统Seq2Seq模型（如基于LSTM的编码器-解码器）通过循环单元逐步传递隐藏状态，如同接力赛中运动员必须依次传递接力棒。而Transformer采用全连接的自注意力网络，允许每个位置直接访问序列中所有位置的信息，就像所有运动员同时观察整个赛场并协同决策。这种架构创新解决了RNN的三大痛点：长距离依赖衰减、训练并行性差、位置编码僵化。

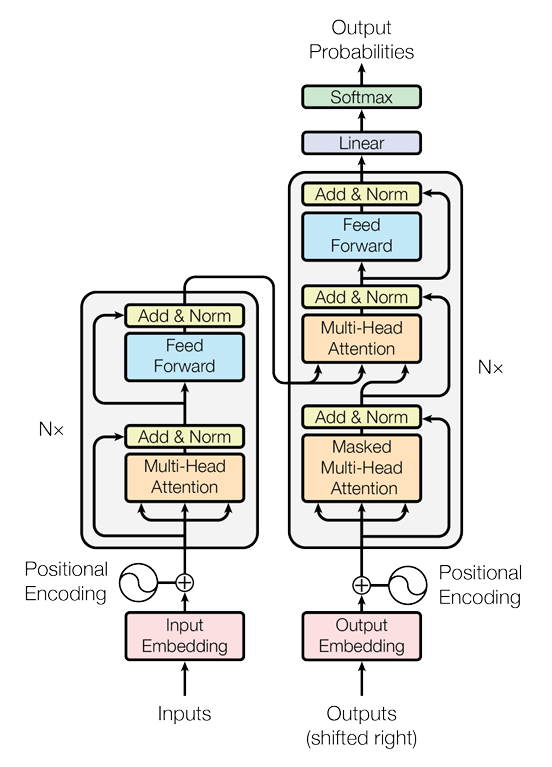
核心组件设计原理

1. 自注意力与多头机制

自注意力机制赋予模型动态聚焦关键信息的能力，而多头设计（Multi-Head Attention）则扩展了这种能力的维度。假设需要分析"银行"一词在"我去银行存钱"和"河岸边的银行"中的不同含义，单头注意力可能仅关注"存钱"或"河岸"等直接关联词，而多头机制允许同时关注：

头1：语法关系（"存钱"→动作对象）
头2：空间关系（"河岸"→方位修饰）
头3：语义消歧（对比金融与地理含义）
通过将查询、键、值矩阵拆分到多个子空间（公式中$h$代表头数）：

\[\text{MultiHead}(Q,K,V) = \text{Concat}(\text{head}_1,...,\text{head}_h)\mathbf{W}^O \]

\[\text{where head}_i = \text{Attention}(Q\mathbf{W}_i^Q, K\mathbf{W}_i^K, V\mathbf{W}_i^V) \]

2. 位置编码的智慧

由于自注意力机制本身不包含位置信息，Transformer通过位置编码（Positional Encoding）注入序列顺序。采用正弦/余弦函数的设计蕴含深刻数学直觉：

\[PE_{(pos,2i)} = \sin(pos/10000^{2i/d_{\text{model}}}) \]

\[PE_{(pos,2i+1)} = \cos(pos/10000^{2i/d_{\text{model}}}) \]

这种编码方式具有两个关键特性：

相对位置可学习 ：对于固定偏移量$k$，$PE_{pos+k}$可以表示为$PE_{pos}$的线性函数
长度外推性：三角函数周期性使模型能处理比训练时更长的序列

这如同给每个文字标注经纬度坐标，模型既能识别"北京→上海"的直线距离（绝对位置），也能理解"第二句比第一句晚0.5秒"（相对时序）。

完整实现代码

以下代码实现简化版Transformer（基于PyTorch）：

python 复制代码

import torch
import torch.nn as nn
import math

class PositionalEncoding(nn.Module):
    def __init__(self, d_model, max_len=5000):
        super().__init__()
        pe = torch.zeros(max_len, d_model)
        position = torch.arange(0, max_len, dtype=torch.float).unsqueeze(1)
        div_term = torch.exp(torch.arange(0, d_model, 2).float() * (-math.log(10000.0)/d_model))
        pe[:, 0::2] = torch.sin(position * div_term)  # 偶数位置正弦
        pe[:, 1::2] = torch.cos(position * div_term)  # 奇数位置余弦
        self.register_buffer('pe', pe)

    def forward(self, x):
        return x + self.pe[:x.size(1), :]

class Transformer(nn.Module):
    def __init__(self, vocab_size, d_model=512, nhead=8, num_layers=6):
        super().__init__()
        self.embedding = nn.Embedding(vocab_size, d_model)
        self.pos_encoder = PositionalEncoding(d_model)
        
        # 编码器层
        encoder_layer = nn.TransformerEncoderLayer(
            d_model=d_model,
            nhead=nhead,
            dim_feedforward=2048,
            dropout=0.1
        )
        self.encoder = nn.TransformerEncoder(encoder_layer, num_layers)
        
        # 解码器层
        decoder_layer = nn.TransformerDecoderLayer(
            d_model=d_model,
            nhead=nhead,
            dim_feedforward=2048,
            dropout=0.1
        )
        self.decoder = nn.TransformerDecoder(decoder_layer, num_layers)
        
        self.fc_out = nn.Linear(d_model, vocab_size)

    def forward(self, src, tgt):
        # 源语言编码
        src_emb = self.pos_encoder(self.embedding(src))
        memory = self.encoder(src_emb)
        
        # 目标语言解码
        tgt_emb = self.pos_encoder(self.embedding(tgt))
        output = self.decoder(tgt_emb, memory)
        
        return self.fc_out(output)

# 示例用法
transformer = Transformer(vocab_size=10000)
src = torch.randint(0, 10000, (32, 50))  # batch_size=32, seq_len=50
tgt = torch.randint(0, 10000, (32, 40))
output = transformer(src, tgt)
print("输出维度:", output.shape)  # [32, 40, 10000]

历史意义与技术辐射

Transformer架构重新定义了序列建模的范式，其影响远超机器翻译的原始应用场景：

双向上下文建模：BERT通过Transformer编码器实现深度双向表征
生成能力突破：GPT系列利用解码器堆叠实现开放域文本生成
跨模态统一：Vision Transformer将图像分块视为序列处理
科学计算革新：AlphaFold 2用Transformer预测蛋白质3D结构

其设计哲学------通过注意力机制建立全局关联，通过位置编码保留序列信息，通过残差连接促进深度训练------已成为现代深度学习架构的通用范式。尽管后续出现的稀疏注意力、线性注意力等改进方案不断优化计算效率，Transformer的核心思想依然如同牛顿定律在经典力学中的地位，持续照亮着人工智能的前沿探索。

2.5 预训练模型与大语言模型

2.5.1 预训练技术

深度学习的深度，就是说，通过不停堆积模型模块把深度拉爆，模型的效果总能达到一个突破。这两年大语言模型在各大NLP任务上的卓越表现证明了一件事情：不管你怎么用巧劲，都比不过对方的火力覆盖。力大真的可以砖飞。

前几天我在百度的一个朋友跟我们吐槽：面到一个小孩，问了几个预训练模型的问题，发现对方居然不知道Elmo模型。这个模型虽然比较简单，是通过堆叠BiLSTM模块实现的，但是它的确是开了预训练语言模型的先河，是预训练方法的始祖（不是GPT）。后来还有一个大模型RWKV，也是证明了纯堆RNN也能做大模型。尽管这并没有成为一种主流方案，但这的确是很重要的两个里程碑工作。

GPT系列预训练模型

在Elmo证明了堆叠模块做预训练好用以后，OpenAI的人就开始打起了Transformer的主意。很明显的一个道理嘛，针对不同的NLP任务（文本分类、情感分析、序列标注、信息抽取、机器翻译等）去设计不同的架构太复杂了，我不如让机器统一学习一个更抽象的东西------语言能力，然后让机器在不同的具体任务中去任务微调，设计任务头模块，让它自适应不同的任务。这就是为什么BERT系列模型例如BERT-BiLSTM-CRF架构能够在多个序列标注任务、信息抽取任务上都有用。因为它的核心就是放在学习文本的语义上，也就是学习更好的词向量表示上。没错，词向量之间亦有好坏之分。

GPT架构只使用了Transformer的Decoder部分，然后不停堆。架构如图所示：

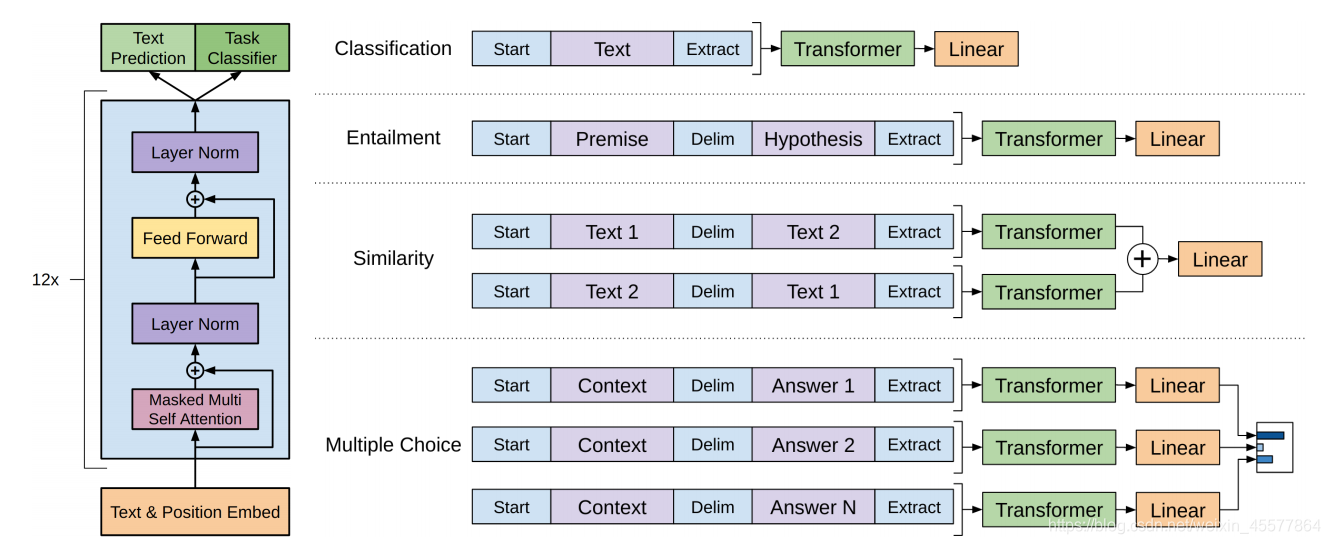
由于只用了一边的Decoder，导致这个模型只能单向传递语义信息。那如果是单向学习语义，我们把它当做一个Next-Word Prediction不就好了？这就是GPT系列架构在学习语料语义信息过程中的核心思想，和很多语言模型类似，它的重心放在了文本生成任务上，重点在于它生成质量的好坏。因此很适合做问答、写作等任务。

GPT（Generative Pre-Training）开创了基于Transformer解码器的预训练范式。其核心思想如同教导一个博览群书的作家：先通过海量文本学习语言规律（预训练），再针对特定写作风格微调（如诗歌、科技论文）。模型架构完全由Transformer解码器堆叠而成，通过掩码自注意力确保每个位置只能关注左侧上下文，模拟人类逐字创作的过程。

核心操作流程：

预训练任务：给定前文预测下一个词，目标函数为：

\[\mathcal{L} = -\sum_{t=1}^T \log P(w_t | w_{<t}) \]

例如输入"人工智能正在___"，模型学习生成"改变"等合理续写。

微调策略：在预训练模型顶部添加任务适配层。对于文本分类任务，将最后一个词的隐藏状态输入分类器：

python 复制代码

class GPTClassifier(nn.Module):
    def __init__(self, gpt_model, num_classes):
        super().__init__()
        self.gpt = gpt_model
        self.classifier = nn.Linear(gpt.config.n_embd, num_classes)
    
    def forward(self, input_ids):
        outputs = self.gpt(input_ids)
        last_hidden = outputs.last_hidden_state[:, -1, :]  # 取最后一个词向量
        return self.classifier(last_hidden)

零样本推理：通过提示工程（Prompt Engineering）激发预训练知识。如将情感分析任务转换为：
text 复制代码
```
评论：这家餐厅服务周到，菜品惊艳。
上述评论的情感倾向是：[MASK]
```
模型可能预测"积极"填充[MASK]位置。

BERT系列预训练模型

那有没有模型用的是Encoder呢？有的。BERT系列模型采用双向的Transformer堆叠，同时学习上文语义和下文语义信息。架构如图所示：

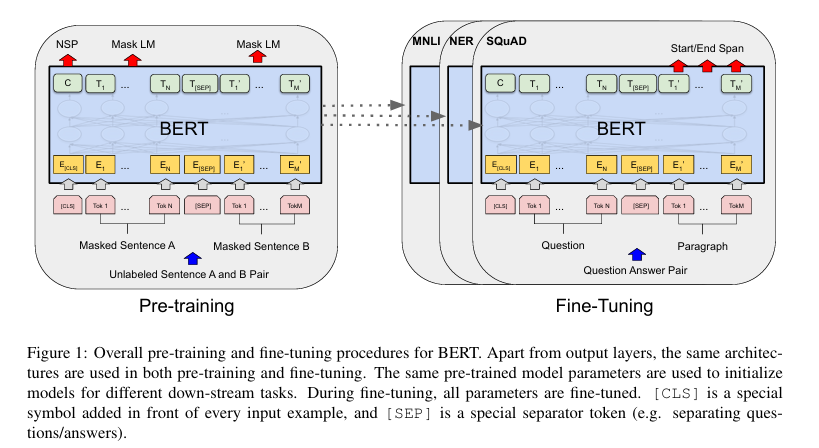
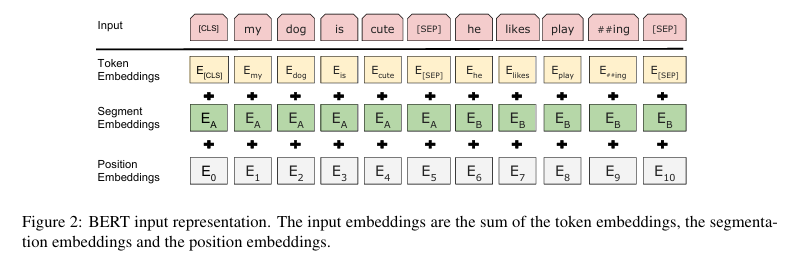
在这个图里面，可以看到，Transformer是双向叠加的。并且，其中出现了三个编码：Token Embedding, Segment Embedding, Position Embedding。也就是词嵌入、分割嵌入、位置嵌入，因为Transformer虽然也适合做序列任务，但是不像RNN一样时序化，对位置信息感知不强，因此需要额外位置编码信息告诉模型哪个词该在哪个位置。分割告诉模型，哪里到哪里构成一个完整的句子。BERT既然能同时学习上下文语义，那么它就不太适合做生成式任务。因为你写作的时候不会先知道下文然后返回来写上文，难道你的小说是先把结局写好了再回过头来写开端么？能同时运用上下文信息的，更多的是像完形填空这样的任务。这也就是BERT训练的核心原理：掩码语言建模，在文段中随机挖掉几个空，然后让模型以完形填空的方式正确填补空白token，以此达到语言能力学习。期间，也有其他一些任务比如next sentence、sentence segmentation、文本分类等来辅助训练语言能力。

关键技术解析：

掩码语言模型：随机遮盖15%的输入词（如"人工智能正在[MASK]世界"），要求模型基于双向上下文预测被遮盖词。部分遮盖词保持原词，防止过拟合：
python 复制代码
```
# 输入序列处理示例
original = ["人工智能", "正在", "改变", "世界"]
masked = ["人工智能", "[MASK]", "改变", "世界"]  # 遮盖"正在"
```

下一句预测：判断两个句子是否连续，学习篇章逻辑关系。如：

text 复制代码

输入：[CLS] 人工智能发展迅猛 [SEP] 相关伦理问题引发讨论 [SEP]
标签：IsNextSentence

微调范式：通过[CLS]标志位的聚合表征实现分类任务。对于问答任务，输出层计算答案起止位置：

\[P_{\text{start}}(i) = \text{softmax}(\mathbf{W}_s \mathbf{h}_i) \]

\[P_{\text{end}}(j) = \text{softmax}(\mathbf{W}_e \mathbf{h}_j) \]

三、BERT词向量实践

以下代码展示如何提取BERT词向量并进行语义分析：

python 复制代码

from transformers import BertTokenizer, BertModel
import torch

# 加载预训练模型
tokenizer = BertTokenizer.from_pretrained('bert-base-chinese')
model = BertModel.from_pretrained('bert-base-chinese')

# 输入处理
text = "自然语言处理是人工智能的核心领域"
inputs = tokenizer(text, return_tensors="pt", padding=True, truncation=True)

# 获取词向量
with torch.no_grad():
    outputs = model(**inputs)
    word_vectors = outputs.last_hidden_state  # [batch, seq_len, hidden_dim]

# 提取特定词向量
tokens = tokenizer.convert_ids_to_tokens(inputs["input_ids"][0])
nlp_index = tokens.index("语言")  # 定位"语言"的位置
nlp_vector = word_vectors[0, nlp_index]  # 获取对应向量

print(f"『语言』的向量维度：{nlp_vector.shape}")  # torch.Size([768])

# 计算句子相似度
def get_sentence_vector(outputs):
    return outputs.last_hidden_state[:, 0, :]  # 取[CLS]向量

sent1 = "深度学习需要大量计算资源"
sent2 = "神经网络训练依赖GPU加速"

vec1 = get_sentence_vector(model(**tokenizer(sent1, return_tensors="pt")))
vec2 = get_sentence_vector(model(**tokenizer(sent2, return_tensors="pt")))

cosine_sim = torch.cosine_similarity(vec1, vec2, dim=-1)
print(f"句子相似度：{cosine_sim.item():.3f}")

关键技术点：

动态词向量：BERT的词向量依赖于上下文，"银行"在"河流银行"与"中央银行"中向量不同
层选择策略：中间层（如第8层）可能捕获语法特征，深层（第12层）更侧重语义
子词处理：对于未登录词如"ChatGPT"，BERT会拆分为["Chat", "##G", "##PT"]并分别编码

维度	GPT	BERT
架构	Transformer解码器堆叠	Transformer编码器堆叠
注意力	单向掩码	完全双向
预训练任务	自回归生成	掩码预测+句子关系
优势场景	文本生成、续写	文本理解、分类

这是两类比较重要的，预训练模型架构。后续当然也有一些预训练模型方法提出，比如PEGASUS、T5、BART、UniLM等。例如BART是一种同时利用Encoder-Decoder的自回归式生成语言模型；RoBERTa、DeBERT等在BERT基础上增强鲁棒性；UniLM提供了统一的预训练范式等。在ChatGPT到来之前，BERT系列模型一直在各大NLP任务（MRC，GEC，QA，NER，文本分类等）中有着重要的应用，并且刷榜很强悍，似乎隐约有一种一统NLP的趋势。

2.5.2 大语言模型

以往的预训练模型往往是提供词向量，然后想要适配不同的NLP任务就要加上不同的任务头。比如，做文本分类我们在BERT上面加一个线性分类层；做NER等序列标注模型我们要加CRF；做文本匹配我们需要用Siamese等度量网络......本身BERT参数量就不小，哪怕是在自己数据集上调也是很要时间的，即使新模型只是在BERT基础上加了个头部，它的负担对我们普通人来说还是太大。我们想能不能不改代码结构、不自己写模型、直接提需求让它自己处理就好，反正只要语言能力在线它机器又不是听不懂人话。于是，一个新的方法------指令微调诞生了。

传统任务微调如同给语言模型套上固定模具，每个任务都需要独立训练数据与模型参数调整，这种范式在面对层出不穷的现实需求时显得笨拙低效。InstructGPT的创新之处在于将"模具"转化为"说明书"，通过引入人类标注的指令-响应对（如"写一首关于秋天的诗：风格要求押韵，包含枫叶意象"）和强化学习技术，让模型学会解析抽象指令背后的潜在意图。这一转变使得模型不再依赖特定任务的标注数据，而是通过理解自然语言指令动态调整行为，标志着AI从"专用工具"向"通用助手"的进化。正是这一过程中，工程师们发现精心设计的提示（Prompt）能显著影响输出质量，由此催生了提示工程这一新兴技术领域，为后续大模型的交互方式奠定基础。

从GPT-3具备的能力出发，当OpenAI的科学家加入一些指令微调以后，他们发现模型可以接受用户的需求给出相应的回答响应。他们想到：这种具备强语言能力的模型一旦放到QA系统或者ChatBot等聊天机器人当中那将是降维打击，因此他们想到把它做成网页聊天应用放出来。2022年11月30日的夜晚，当OpenAI向公众开放ChatGPT访问时，技术界亲历了AI发展的"寒武纪大爆发"。这个基于GPT-3.5架构的对话模型展现出前所未有的语言理解与生成能力：它不仅能流畅解答编程问题、撰写学术论文，还会在用户追问时承认知识边界，甚至主动纠正对话中的逻辑矛盾。凌晨三点的社交媒体上，从业者们在惊叹中传阅着与AI讨论哲学悖论的对话截图，学者们连夜分析其响应机制，初创公司则紧急召开会议调整产品路线。这个夜晚不仅重新定义了人机交互的边界，更以单日百万用户的爆发式增长，宣告了大模型技术从实验室到大众市场的历史性跨越。《浪潮之巅》的作者吴军表示------ChatGPT真正能火出圈的原因，不是GPT，而是Chat。因为GPT语言模型早就有了，并不是新东西，但是冰冷的词向量除了NLP工程师没人知道它怎么用；但对话式、交互式、线性的人机交互模式，让老百姓都见识了NLP对他们的降维打击。

大语言模型通常指参数规模超过千亿、训练数据涵盖万亿token的深度神经网络，其核心特征在于涌现出小模型不具备的复杂推理与泛化能力。一个现代大模型的诞生始于对海量互联网文本的预训练------数万张GPU组成的计算集群持续运转数周，通过自监督学习捕捉语言统计规律；随后进入指令微调阶段，工程师使用精心构造的对话数据集调整模型行为，使其输出更符合人类价值观；最终通过基于人类反馈的强化学习（RLHF），让模型在安全性与有用性之间达到平衡。整个过程如同培育数字大脑：预训练构建基础认知架构，微调塑造社会行为规范，强化学习则注入价值判断的"道德罗盘"。关于大语言模型本身的一些知识，我在后面的章节中会简介。

2023年掀起的"百模大战"中，全球科技企业竞相发布千亿级大模型，却在同质化竞争中陷入技术瓶颈。深度求索（DeepSeek）团队独辟蹊径，于2024年推出Deepseek-R1架构，其创新的混合专家系统（MoE）与动态令牌激活机制，在保持175B参数规模的同时，将推理成本降低至传统架构的1/7。该模型在长上下文理解方面实现突破，可精准处理长达128k token的法律文书分析与跨文档知识关联，其创新的"思维链蒸馏"技术更是将复杂逻辑推理的准确率提升23%。作为国产大模型的代表，Deepseek-R1不仅在国际权威评测中斩获7项SOTA，更通过开源生态建设推动全球逾500家企业实现智能化升级，重塑了大模型技术的创新格局与产业落地路径。至此，中国人也有了21世纪的新"原子弹"。

自然语言处理入门【第二章】：语言模型

2.1 语言模型

2.1.1 语言是可计算的

2.1.2 N-Grams语言模型

2. 基于词频统计的Next-Word概率估计（以Bigram为例）

3. Python代码实现（Bigram模型）

4. 数据平滑技术

5. N-Gram在NLP中的应用

6. N-Gram模型的局限性

2.2 神经语言模型

2.2.1 神经网络与深度学习

2.2.2 前馈神经网络作为语言模型

2.2.3 循环神经网络作为语言模型

1. 循环神经网络的基本原理与训练

2. LSTM的设计思想、改进点与数学原理

2.3 词向量模型

2.3.1 词向量是语言模型的副产物

向量运算的语义意义

实践示例

自然语言处理意义

2.3.2 word2vec词向量模型

一、提出动机与范式突破

二、模型架构原理

三、实践：基于Gensim的自定义训练

四、模型特性分析

2.4 Attention is All You Need

2.4.1 注意力机制

2.4.2 Transformer模型

核心组件设计原理

完整实现代码

历史意义与技术辐射

2.5 预训练模型与大语言模型

2.5.1 预训练技术

GPT系列预训练模型

BERT系列预训练模型

三、BERT词向量实践

2.5.2 大语言模型