C#中的常见集合
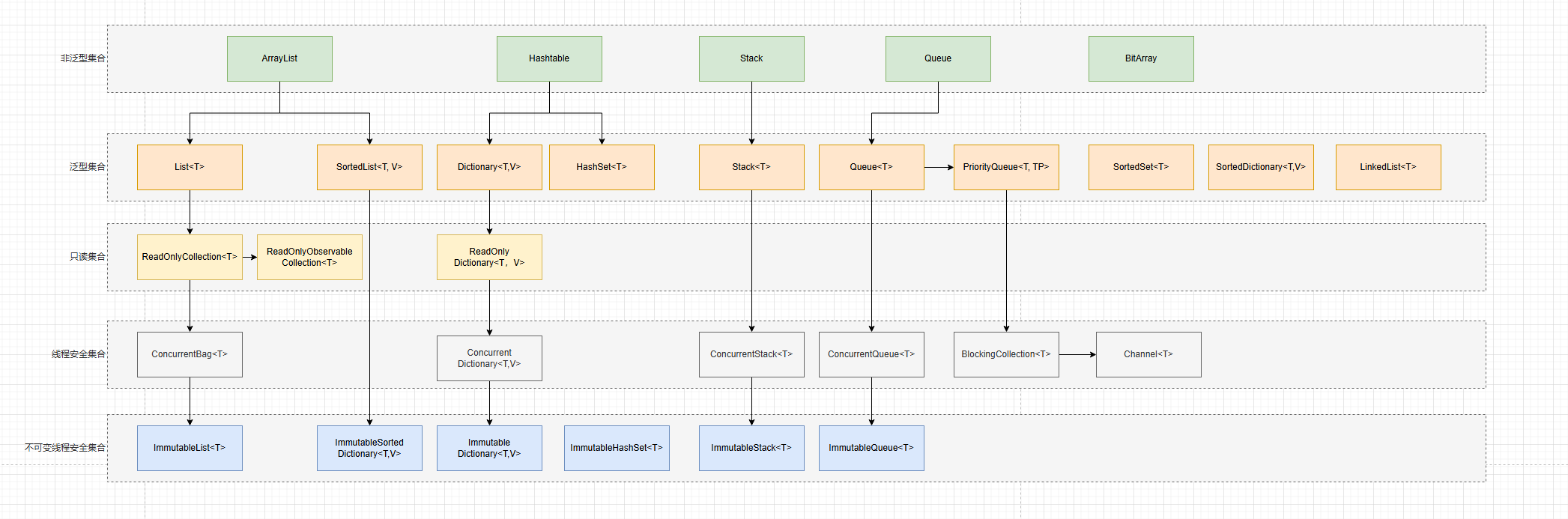
注意,箭头线不代表继承关系,只代表功能上的加强,如有错误,欢迎指出。
泛型集合时间复杂度
| 集合类型 | 添加 | 删除 | 查找 | 访问(索引/键) | 遍历 | 备注 |
|---|---|---|---|---|---|---|
List<T> |
O(1)(均摊) | O(n) | O(n) | O(1) | O(n) | 动态数组;删除/插入中间元素需移动数据 |
SortedList<T> |
O(n) | O(n) | O(log n) | O(1)(按索引) | O(n) | 内部维护排序数组;插入需移动元素 |
Dictionary<T,K> |
O(1) | O(1) | O(1) | O(1) | O(n) | 哈希表实现;最坏情况 O(n)(哈希冲突) |
HashSet<T> |
O(1) | O(1) | O(1) | - | O(n) | 哈希表实现;同 Dictionary 的哈希行为 |
Stack<T> |
O(1)(Push) | O(1)(Pop) | - | - | - | 数组或链表实现 |
Queue<T> |
O(1)(Enqueue) | O(1)(Dequeue) | - | - | - | 数组或链表实现 |
PriorityQueue<T> |
O(log n) | O(log n) | - | O(1)(Peek) | - | 基于堆结构实现 |
SortedSet<T> |
O(log n) | O(log n) | O(log n) | - | O(n) | 基于平衡二叉搜索树(如红黑树) |
SortedDictionary<T,K> |
O(log n) | O(log n) | O(log n) | - | O(n) | 基于平衡二叉搜索树(类似 SortedSet) |
LinkedList<T> |
O(1)(头/尾) | O(1)(已知节点) | O(n) | - | O(n) | 双向链表;查找需遍历 |
线程安全集合时间复杂度
| 集合类型 | 添加 | 删除 | 查找 | 访问(索引/键) | 遍历 | 备注 |
|---|---|---|---|---|---|---|
ConcurrentBag<T> |
平均 O(1) | 平均 O(1) | O(n) | 不支持 | O(n) | 线程安全无序集合,适用于多生产者 - 多消费者场景 |
ConcurrentDictionary<TKey, TValue> |
平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | O(n) | 基于分段锁和哈希表实现的线程安全字典 |
ConcurrentStack<T> |
平均 O(1) | 平均 O(1) | O(n) | 不支持 | O(n) | 线程安全的后进先出(LIFO)集合 |
ConcurrentQueue<T> |
平均 O(1),最坏 O(n) | 平均 O(1) | O(n) | 不支持 | O(n) | 线程安全的先进先出(FIFO)集合 |
不可变集合时间复杂度
以下是 C# 中 ImmutableList<T>、ImmutableSortedDictionary<TKey, TValue>、ImmutableDictionary<TKey, TValue>、ImmutableHashSet<T>、ImmutableStack<T> 和 ImmutableQueue<T> 这些不可变集合常见操作的时间复杂度表格:
| 集合类型 | 添加 | 删除 | 查找 | 访问(索引/键) | 遍历 | 备注 |
|---|---|---|---|---|---|---|
ImmutableList<T> |
O(n) | O(n) | O(n) | O(1) | O(n) | 基于数组实现的不可变列表,每次修改操作都会创建新列表,访问指定索引元素较快 |
ImmutableSortedDictionary<TKey, TValue> |
O(log n) | O(log n) | O(log n) | O(log n) | O(n) | 基于红黑树实现的按键排序的不可变字典,元素按键排序,操作复杂度基于树的高度 |
ImmutableDictionary<TKey, TValue> |
平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | O(n) | 基于哈希表实现的不可变字典,操作复杂度受哈希冲突影响 |
ImmutableHashSet<T> |
平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | 不适用 | O(n) | 基于哈希表实现的不可变集合,存储唯一元素,操作复杂度受哈希冲突影响 |
ImmutableStack<T> |
O(1) | O(1) | O(n) | 不适用 | O(n) | 基于链表实现的不可变栈,后进先出,添加和删除操作在栈顶进行 |
ImmutableQueue<T> |
O(1) | O(1) | O(n) | 不适用 | O(n) | 基于链表实现的不可变队列,先进先出,添加和删除操作分别在队尾和队首进行 |
只读集合时间复杂度
| 集合类型 | 添加 | 删除 | 查找 | 访问(索引/键) | 遍历 | 备注 |
|---|---|---|---|---|---|---|
ReadOnlyCollection<T> |
不支持 | 不支持 | O(n) | O(1) | O(n) | 对 IList<T> 的只读包装,可通过索引直接访问元素,查找需遍历集合 |
ReadOnlyObservableCollection<T> |
不支持 | 不支持 | O(n) | O(1) | O(n) | 继承自 ReadOnlyCollection<T> 且实现 INotifyCollectionChanged,基本操作复杂度与 ReadOnlyCollection<T> 相同 |
ReadOnlyDictionary<TKey, TValue> |
不支持 | 不支持 | 平均 O(1),最坏 O(n) | 平均 O(1),最坏 O(n) | O(n) | 对 IDictionary<TKey, TValue> 的只读包装,基于哈希表,操作复杂度受哈希冲突影响 |
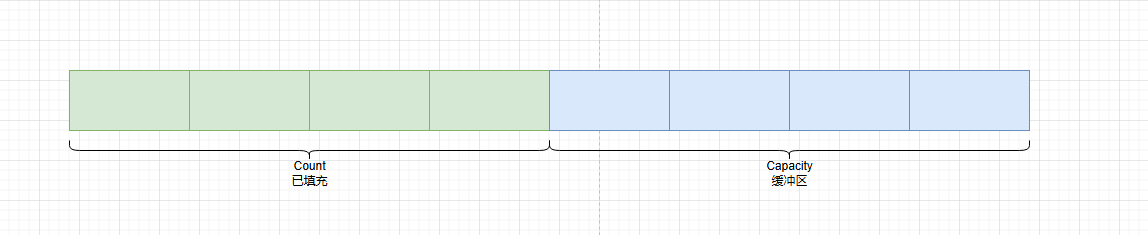
List
当你创建一个新的List对象时,若没有指定初始容量,默认为0,不过当第一个元素被添加进去时,它会自动将容量初始化为4.并在下次扩容时,以双倍的容量进行扩容。
List.Insert(0, item) 的坑
List基于数组实现,数组在内存中是连续存储的。当使用 Insert(0, item) 在列表开头插入元素时,列表中现有的所有元素都需要向后移动一个位置,以便为新元素腾出空间。这意味着插入操作的时间复杂度为O(n) ,其中n是列表中现有元素的数量。元素数量越多,移动元素所花费的时间就越长,性能也就越低。
public void Insert(int index, T item)
{
// Note that insertions at the end are legal.
if ((uint)index > (uint)_size)
{
ThrowHelper.ThrowArgumentOutOfRangeException(ExceptionArgument.index, ExceptionResource.ArgumentOutOfRange_ListInsert);
}
if (_size == _items.Length) Grow(_size + 1);
if (index < _size)
{
//如果index很靠前,且数组size很大的话。这将是一场灾难。
Array.Copy(_items, index, _items, index + 1, _size - index);
}
_items[index] = item;
_size++;
_version++;
}HashSet/Dictionary
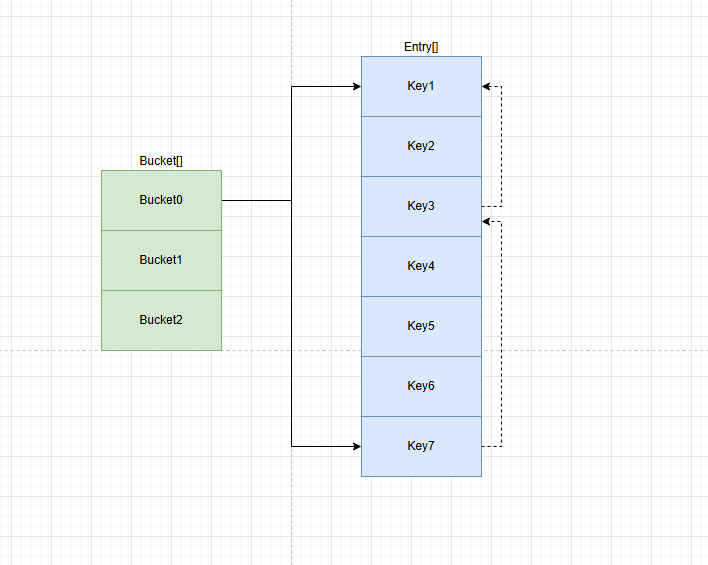
Dictionary<TKey, TValue> 的底层结构主要由以下几个部分组成:
- 桶(Bucket)数组:这是一个一维数组,数组的每个元素称为一个桶。桶数组的大小是 Dictionary 的容量,初始容量通常是一个较小的质数,后续会根据元素数量的增加而动态调整。
- 条目(Entry)数组:每个桶对应一个或多个条目,条目是一个结构体,包含三个重要的字段:
*. int hashCode:键的哈希码,用于确定键在桶数组中的位置。
*. int next:指向下一个条目的索引,用于处理哈希冲突。如果该值为 -1,表示这是该桶中的最后一个条目。
*. TKey key:存储的键。
*. TValue value:存储的值。
Add的坑
private bool TryInsert(TKey key, TValue value, InsertionBehavior behavior)
{
//计算出key的hash
uint hashCode = (uint)((typeof(TKey).IsValueType && comparer == null) ? key.GetHashCode() : comparer!.GetHashCode(key));
//将哈希码与桶数组的长度进行取模运算(hashCode % bucket.Length),得到该键值对应在桶数组中的索引位置。
ref int bucket = ref GetBucket(hashCode);
int i = bucket - 1; // Value in _buckets is 1-based
uint collisionCount = 0;
while (true)
{
// Should be a while loop https://github.com/dotnet/runtime/issues/9422
// Test uint in if rather than loop condition to drop range check for following array access
if ((uint)i >= (uint)entries.Length)
{
break;
}
//
if (entries[i].hashCode == hashCode && comparer.Equals(entries[i].key, key))
{
return false;
}
//如果该桶已经有其他条目(即发生了哈希冲突),则通过 next 字段将新条目链接到该桶的链表中。
i = entries[i].next;
collisionCount++;
//如果循环次数>Entry的长度,说明有死循环,抛出异常。
if (collisionCount > (uint)entries.Length)
{
// 在Framework时代,并发情况下会导致entries[i].next被错误定位。
// 从而形成一个死链表,导致Contains查询时,陷入死循环,CPU异常高。
// 在.NET Core中,通过collisionCount来计数,从而规避死循环。
ThrowHelper.ThrowInvalidOperationException_ConcurrentOperationsNotSupported();
}
}
}ConcurrentDictionary
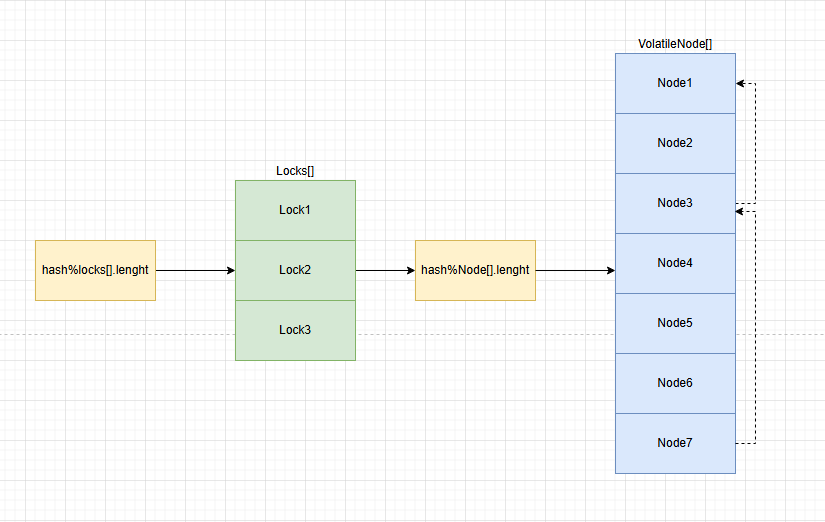
ConcurrentDictionary<TKey, TValue> 的底层核心是由多个分段(Segment)组成,每个分段本质上是一个小型的哈希表,并且每个分段都有自己独立的锁。这种设计将整个字典划分为多个部分,不同线程可以同时访问不同的分段,从而减少锁的竞争,提高并发性能。
简单来说就是多个Dictionary组合
- VolatileNode[]
内部的Node类和Dictionary的Entry一致
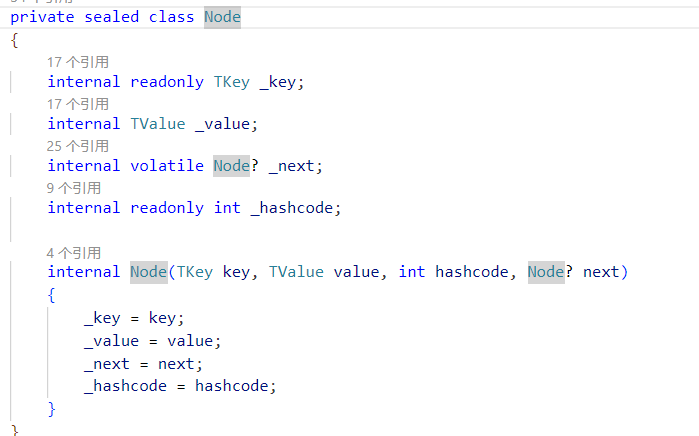
- Locks[]
将一个大锁拆成多个小锁,提高锁的颗粒度,尽可能小的避免锁竞争。
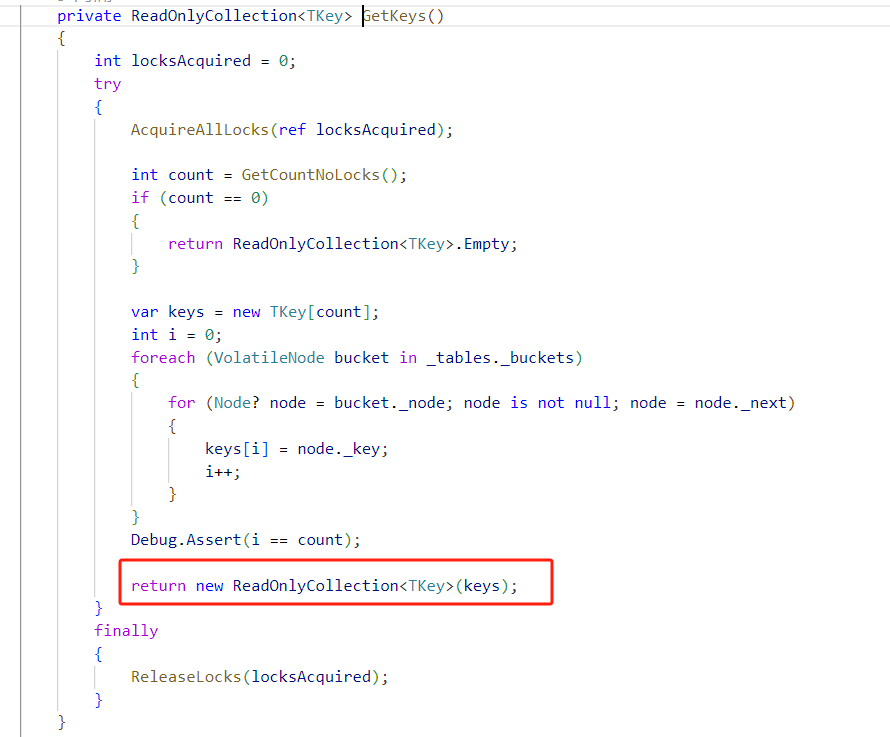
keys/values的坑
不要高频次调用属性,因为它们会返回一个全新的List
ValueFactory的坑
在使用ConcurrentDictionary的过程中,大家会理所当然认为所有操作是线程安全的。但面对GetOrAdd/GetOrUpdate中的ValueFactory方法时,却是线程不安全的。
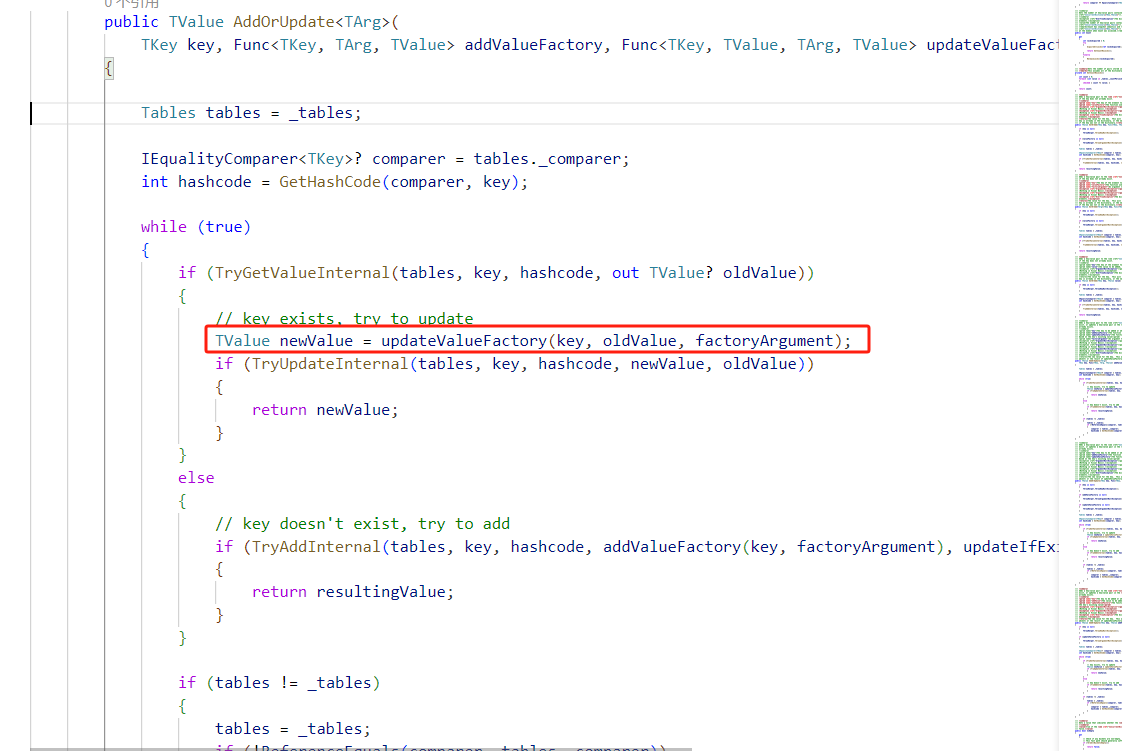
原因也很简单,ValueFactory会被先执行,再执行从TryUpdateInternal。因此,你有几个线程就会重复执行几次。
举个例子,偷懒用其它大佬的例子。https://www.cnblogs.com/CreateMyself/p/6086752.html
如果要确保线程安全,需要搭配Lazy<>.
ConcurrentQueue
ConcurrentQueue 底层主要基于链表(Linked List)数据结构实现,链表是一种动态的数据结构,由一系列节点(ConcurrentQueueSegment)组成,每个节点包含一个数据元素和一个指向下一个节点的引用。为了保证线程安全,ConcurrentQueue 在链表的基础上使用了无锁(Lock - Free)算法,主要借助原子操作(如 Interlocked 类提供的方法)来避免传统锁带来的性能开销和潜在的死锁问题
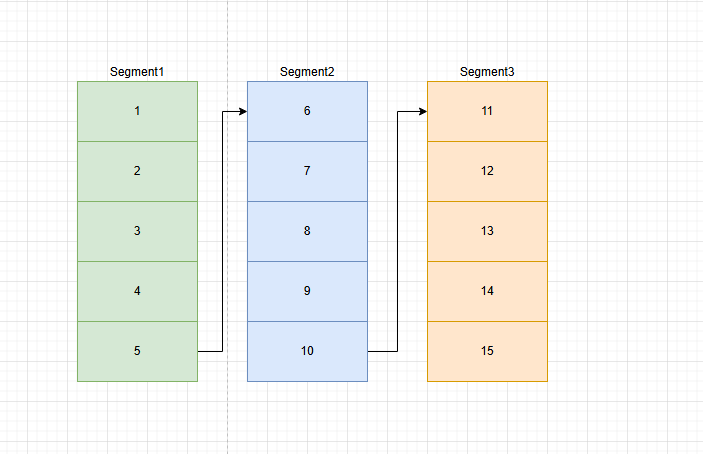
- 头指针(head)
头指针指向队列的第一个节点,用于出队操作 - 尾指针(tail)
尾指针指向队列的最后一个节点,用于入队操作
Count的坑
不要高频次调用Count属性,因为内部调用逻辑非常复杂,需要遍历每一个Segment的head,tail之间的差值,动态计算出最终的大小,且还有加锁操作,消耗也不低。
点击查看代码
public int Count
{
get
{
SpinWait spinner = default;
while (true)
{
// Capture the head and tail, as well as the head's head and tail.
ConcurrentQueueSegment<T> head = _head;
ConcurrentQueueSegment<T> tail = _tail;
int headHead = Volatile.Read(ref head._headAndTail.Head);
int headTail = Volatile.Read(ref head._headAndTail.Tail);
if (head == tail)
{
// There was a single segment in the queue. If the captured segments still
// match, then we can trust the values to compute the segment's count. (It's
// theoretically possible the values could have looped around and still exactly match,
// but that would required at least ~4 billion elements to have been enqueued and
// dequeued between the reads.)
if (head == _head &&
tail == _tail &&
headHead == Volatile.Read(ref head._headAndTail.Head) &&
headTail == Volatile.Read(ref head._headAndTail.Tail))
{
return GetCount(head, headHead, headTail);
}
}
else if (head._nextSegment == tail)
{
// There were two segments in the queue. Get the positions from the tail, and as above,
// if the captured values match the previous reads, return the sum of the counts from both segments.
int tailHead = Volatile.Read(ref tail._headAndTail.Head);
int tailTail = Volatile.Read(ref tail._headAndTail.Tail);
if (head == _head &&
tail == _tail &&
headHead == Volatile.Read(ref head._headAndTail.Head) &&
headTail == Volatile.Read(ref head._headAndTail.Tail) &&
tailHead == Volatile.Read(ref tail._headAndTail.Head) &&
tailTail == Volatile.Read(ref tail._headAndTail.Tail))
{
return GetCount(head, headHead, headTail) + GetCount(tail, tailHead, tailTail);
}
}
else
{
// There were more than two segments in the queue. Fall back to taking the cross-segment lock,
// which will ensure that the head and tail segments we read are stable (since the lock is needed to change them);
// for the two-segment case above, we can simply rely on subsequent comparisons, but for the two+ case, we need
// to be able to trust the internal segments between the head and tail.
lock (_crossSegmentLock)
{
// Now that we hold the lock, re-read the previously captured head and tail segments and head positions.
// If either has changed, start over.
if (head == _head && tail == _tail)
{
// Get the positions from the tail, and as above, if the captured values match the previous reads,
// we can use the values to compute the count of the head and tail segments.
int tailHead = Volatile.Read(ref tail._headAndTail.Head);
int tailTail = Volatile.Read(ref tail._headAndTail.Tail);
if (headHead == Volatile.Read(ref head._headAndTail.Head) &&
headTail == Volatile.Read(ref head._headAndTail.Tail) &&
tailHead == Volatile.Read(ref tail._headAndTail.Head) &&
tailTail == Volatile.Read(ref tail._headAndTail.Tail))
{
// We got stable values for the head and tail segments, so we can just compute the sizes
// based on those and add them. Note that this and the below additions to count may overflow: previous
// implementations allowed that, so we don't check, either, and it is theoretically possible for the
// queue to store more than int.MaxValue items.
int count = GetCount(head, headHead, headTail) + GetCount(tail, tailHead, tailTail);
// Now add the counts for each internal segment. Since there were segments before these,
// for counting purposes we consider them to start at the 0th element, and since there is at
// least one segment after each, each was frozen, so we can count until each's frozen tail.
// With the cross-segment lock held, we're guaranteed that all of these internal segments are
// consistent, as the head and tail segment can't be changed while we're holding the lock, and
// dequeueing and enqueueing can only be done from the head and tail segments, which these aren't.
for (ConcurrentQueueSegment<T> s = head._nextSegment!; s != tail; s = s._nextSegment!)
{
Debug.Assert(s._frozenForEnqueues, "Internal segment must be frozen as there's a following segment.");
count += s._headAndTail.Tail - s.FreezeOffset;
}
return count;
}
}
}
}
// We raced with enqueues/dequeues and captured an inconsistent picture of the queue.
// Spin and try again.
spinner.SpinOnce();
}
}
}
private static int GetCount(ConcurrentQueueSegment<T> s, int head, int tail)
{
if (head != tail && head != tail - s.FreezeOffset)
{
head &= s._slotsMask;
tail &= s._slotsMask;
return head < tail ? tail - head : s._slots.Length - head + tail;
}
return 0;
}