最小费用最大流问题的 SSP 算法

我们已经了解最大流问题，其目标是通过网络中的各条边传输流量，尽可能地从源点流向汇点。通过经典的算法，如 Ford-Fulkerson 增广，我们能够找到一种方式，最大化从源点到汇点的流量。

然而，最大流问题的基本形式并没有考虑流动的成本。一个图的最大流值是一个固定数，可以由多种算法算出来，但具体流法可以有多种，假如每条边单位流量的费用不同，要在所有最大的流中选出费用最小的一个，就成为了最小费用最大流问题（简称费用流）。在实际应用中，很多网络问题并不仅仅关心流量的最大化，更需要关注流动的费用，例如在交通运输、通信网络、供应链优化等场景中，除了流量外，每条边的费用也会对整体最优解产生重要影响。

这个问题比最大流更难，但是我们可以借鉴最大流的思路。为了求解最小费用最大流问题，最常见的方法仍是增广路算法。在这种方法中，算法仍然通过不断在残量网络中寻找增广路径，将流量推向网络中的不同路径，同时更新网络中的流量和费用。

费用流，增广路与残差网络

最小费用最大流问题是经典最大流问题的一个扩展，其核心在于在保证流量最大化的同时，最小化流动的总费用。为了更好地理解这个问题，我们首先从数学上定义"费用流"问题。

假设我们有一个带权有向图 $ G = (V, E) $。每条边 $ (u, v) \in E $ 具有三个属性：容量 $ c(u, v) $，费用 $ a(u, v) $，以及流量 $ f(u, v) $，其中：

• $ c(u, v) $ 表示从节点 $ u $ 到节点 $ v $ 的最大流量（容量）。
• $ a(u, v) $ 表示单位流量的费用，费用允许是负数。但是，负费用边可能导致负费用环出现，这会让问题性质发生一些变化，需要额外的算法处理，本文不考虑负费用环的情况。
• $ f(u, v) $ 表示从 $ u $ 到 $ v $ 上流动的流量。

我们定义网络中的流量 $ f $ 为满足以下约束条件的一个集合：

1. 容量约束：对于每一条边，流量 $ f(u, v) $ 必须满足 $ 0 \leq f(u, v) \leq c(u, v) $。
2. 流量平衡：除了源点和汇点外，对于每个节点，流入节点的总流量等于流出节点的总流量.

以上和最大流问题都一样。而在最小费用最大流问题中，我们的目标是最大化从源点到汇点的流量，在所有使得流量达到最大流的方案里，最小化流动的总费用。总费用可以通过以下公式计算：

\[\text{Total Cost} = \sum_{(u, v) \in E} a(u, v) \cdot f(u, v). \]

因此，我们的目标可以表示为一个最优化问题：

\[\max \quad \text{Flow}(s, t) \quad \text{subject to} \quad \text{Cost} = \sum_{(u, v) \in E} a(u, v) \cdot f(u, v). \]

我们已经知道 FF 增广是最大流的经典解法，为了求解最小费用最大流问题，增广路算法仍是最基本的解法。增广路算法的核心思想是不断通过残量网络寻找增广路径，并在找到路径后通过流量的增广来推动流量的传递。我们仍使用残量网络来表示当前网络中的流动情况，并通过更新残量网络来实现流量的增广。

在传统的最大流问题中，残量网络的定义相对简单，边的残量容量是当前边的容量减去已经流过的流量，即：

\[c_f(u, v) = c(u, v) - f(u, v). \]

但是，在最小费用最大流问题中，残量网络的边还增加了一个费用属性。具体来说，对于每一条边 $ (u, v) $，我们有两个残量边：

1. 正向残量边 $ (u, v) $ 的残量容量为 $ c_f(u, v) = c(u, v) - f(u, v) $，其费用为 $ a(u, v) $。
2. 反向残量边 $ (v, u) $ 的残量容量为 $ c_f(v, u) = f(u, v) $，其费用为 $ -a(u, v) $，表示撤销流动时的返还费用。

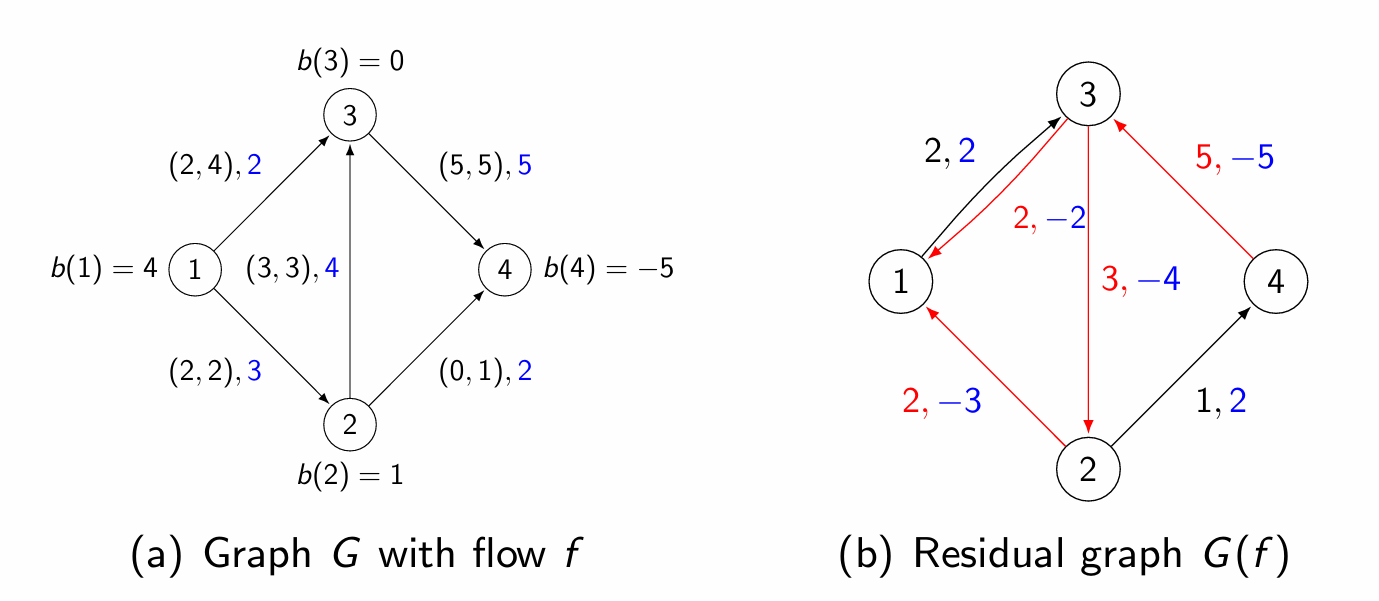
这些反向边的引入使得增广路径的搜索不仅涉及容量的限制，还需要在考虑费用的同时进行流量的调整。这就导致了我们在最小费用最大流问题中，需要使用更复杂的路径搜索算法。

SSP 算法

在传统的最大流问题中，路径的选择依赖于图的残量容量 ，即每条边的剩余可用容量。在增广路算法中，通常通过**广度优先搜索（BFS）**来寻找路径，因为 BFS 可以有效找到最短增广路径（如 EK 和 dinic），从源点到汇点的流量路径。不过，这里"最短"是假设边长度均为 1，而不考虑边的费用。

在最小费用最大流问题中，路径搜索不再是简单的容量最大化问题，而是要同时最小化费用。因此，路径的选择必须基于边的费用，而非仅仅依赖于容量。这就引出了带权最短路径问题，此时应该将费用视为最短路的边权，在带有边费用的图中，找到从源点到汇点的最短路径。

这就意味着，相比于最大流，费用流问题每次增广增加流量时，总是先选择最便宜的路线，这样的贪心策略使得达到最大流时花费的费用最少。

为什么选择 Bellman-Ford / SPFA ？

即使初始图边权都是非负数，反向边的费用也会导致负数出现。因此，Dijkstra 算法不能直接使用。

Bellman-Ford / SPFA 算法能够正确处理带有负权边的图。适用于最小费用最大流问题中带有负权边的网络。除非有负费用环存在（因为负环会使得 SPFA 算法失效）。

可以使用归纳法证明，只要初始图不存在负费用环，运行过程中的残量网络也不会出现负费用环。

算法运行流程

• 构建残量网络：初始化网络，设置所有边的容量、费用和反向边。
• 使用SPFA进行路径搜索：以费用为权重，通过 SPFA 算法寻找从源点到汇点的最短路径。每次 SPFA 的运行都会考虑边的费用，确保路径上的流量费用最小。
• 增广流量 ：仅沿着找到的最短路径增广流量，并更新残量网络中的容量和费用。具体来说和 ek 算法相似：
  1. 根据增广路径的残量容量计算能够增广的流量。
  2. 更新路径上每条边的流量，并调整其反向边的容量。
  3. 更新总流量和总费用
• 重复过程：不断重复路径搜索和增广流量的过程，直到没有增广路径为止。

// spfa 版本
class Graph {
    struct Edge {
        int v, res, next, cost;
        Edge(int v, int res, int cost, int next) : v(v), res(res), cost(cost), next(next) {}
    };

    vector<int> head;
    vector<Edge> edges;
    int n, m, s, t;

public:
    void addEdge(int u, int v, int cap, int cost) {
        // 同时添加两侧边，便于残量网络的构建
        edges.emplace_back(v, cap, cost, head[u]);
        head[u] = edges.size() - 1;
        edges.emplace_back(u, 0, -cost, head[v]);
        head[v] = edges.size() - 1;
    }

    Graph(int n, int m, int s, int t) : n(n), m(m), s(s), t(t), head(n+1, -1) {
        edges.reserve(m * 2);
    }

    pair<int, int> ssp() {
        int res = 0, totalCost = 0; 
        vector<int> dist(n+1), curHead(n+1), path(n+1);
        vector<bool> vis(n+1);

        for (;;) {
            fill(dist.begin(), dist.end(), INT_MAX);
            fill(vis.begin(), vis.end(), false);

            queue<int> q;
            q.push(s);
            dist[s] = 0;
            path[s] = -1;

            while (!q.empty()) {
                int u = q.front();
                q.pop();
                vis[u] = false;

                for (int i = head[u]; i != -1; i = edges[i].next) {
                    auto [v, res, _, cost] = edges[i];
                    if (res > 0 && dist[v] > dist[u] + cost) {
                        dist[v] = dist[u] + cost;
                        path[v] = i;
                        if (!vis[v]) {
                            vis[v] = true;
                            q.push(v);
                        }
                    }
                }
            }
            if (dist[t] == INT_MAX) break;

            int minFlow = INT_MAX;
            for (int i = path[t]; i != -1; i = path[edges[i ^ 1].v]) {
                auto [v, res, _, cost] = edges[i];
                minFlow = min(minFlow, res);
            }
            for (int i = path[t]; i != -1; i = path[edges[i ^ 1].v]) {
                auto [v, res, _, cost] = edges[i];
                edges[i].res -= minFlow;
                edges[i ^ 1].res += minFlow;
            }
            res += minFlow;
            totalCost += minFlow * dist[t];
        } return {res, totalCost};
    }
};

似乎可以将最小费用最大流问题的求解视为将传统的最大流增广算法（如 Edmonds-Karp 或 Dinic）中的 BFS 寻路替换为带权图的最短路算法（如 SPFA）。注意，这只能帮助理解，实际上本算法虽然仍是一种增广，但已经不满足 Edmonds-Karp 或 Dinic "每次寻找最短边数增广路的性质了"，而算另一种 FF 增广的实现。

复杂度分析：超多项式的上界

对于最大流问题，算法如 Edmonds-Karp 和 Dinic 每次寻找最短的增广路径，这保证了算法的复杂度上界是多项式的（如 dinic 的 \(O(V^2E)\)）。然而，在最小费用最大流问题中，增广路径的选择不仅仅是容量最大化，而是费用最小化。因此，虽然我们每次仍然寻找最短增广路径，但这条费用最低的路径不一定是经过最少边的路径，从而导致算法的复杂度上界不再稳定（因为其复杂度不仅取决于图规模，还取决于流量的值域），在最坏情况下是超多项式的。

也是因此，上面的代码也可以改用类似 dinic 的当前弧多路增广，但复杂度不会有提升。使用 dinic 实现时，由于图中没有负环，但是可能存在零费用环；所以 \(dist[v] = dist[u] + cost\) 不能判断 \(u\) 为 \(v\) 的最短路径前驱，也应该向上文一样构造最短路径树。

不过，在实际的随机数据下，算法仍然能够有效运行，尤其是在图较为稀疏时，SPFA的优化能够显著加速搜索过程。

Primal Dual 方法

在凸优化中，"对偶问题"是与原问题（Primal Problem）相关的另一个优化问题。通常，通过对偶问题，我们可以得到原问题的一些边界或其他性质的理解。在本问题中，原问题是寻求最小的费用流量，而对偶问题则关注网络中每条边的"潜在权重"，这些权重的选择会影响最终的最优解。

对于程序员来说，Primal-Dual 方法的关键在于其核心操作：我们通过设置每个节点的"潜在权重"来避免负权边，通过潜在权重调整边的权重，来确保图中所有边的权重非负。这个调整可以使得我们在最短路径问题中使用 Dijkstra 算法。

具体来说，在算法开始前，从原点运行一次 SPFA，将每个点的初始距离设置为其势能 \(π(u)\)；在此后运行最短路时，都将 \((u, v, w)\) 的边权视为 \(w + π(u) - π(v)\)，参考 Johnson 算法的相同思路，我们可以保证边权非负（可以使用高效的 dijkstra），且新旧边权的图中源点到汇点的最短路相同。

而每一次增广结束后，又可能产生负边，如何调整权重呢？一个简单的方法每一轮都像开始一样，让所有点的权重增加一个修正后的距离，保持非负性和等价性。