【Unity】投影矩阵和线性深度推导

网络上有很多投影矩阵的推导，也有很多声称是基于 Unity 的，但和我的实测都不一致（现在看来是因为这些文章并不全面），此外有一些 Unity 本身的函数我也搞不懂它的原理，遂最终选择自行研究，总算把这些问题解决了。

现在通过这篇文章，你就可以完全搞懂 Unity 的投影矩阵是啥样，又是怎么来的。以及 Unity 逆推线性深度的函数是如何实现的。不过该文章也不是完全面向小白的，至少你应该对这些矩阵本来就有大概的了解。

渲染中的矩阵变换

渲染过程中将模型顶点转换到显卡设备的 NDC（标准设备坐标系）中，共要进行以下几个矩阵变换：

物体到世界空间矩阵（物体矩阵）
世界到视图空间矩阵（视图矩阵）
视图到剪辑空间（采用齐次坐标的 NDC 空间）矩阵（投影矩阵）

物体到世界空间矩阵就是正常的 TRS（转移,旋转,缩放）矩阵，不是本文的研究对象，在 Unity 中主要是"视图矩阵"和"投影矩阵"有特殊的地方。

视图矩阵

视图矩阵本质就是不受缩放影响的相机的 TRS 矩阵的逆矩阵。除此之外，在 Unity 中该矩阵还有个特别的地方。

虽然 Unity 是左手坐标系引擎，但它的视图空间却是用的右手坐标系的（z 轴正负与左手坐标系相反），更官方的表述是 Unity 采用的是 opengl 风格的视图矩阵。故最终会对 z 轴进行反转，使相机正前方为-z（即会对矩阵中的 m33 （z 轴系数）取反）。

虽然这一操作让人感觉有些不适，但也便于了我们后续将深度计算为 D3D 风格的 1-0（越远深度值越小），而不是传统风格的 0-1（越远深度值越大）。

投影矩阵

投影矩阵用于将视图矩阵的结果转换到剪辑空间，但具体根据当前所使用的图形 API 不同，其投影矩阵和 NDC 都会有所差异：

https://docs.unity.cn/cn/2022.3/Manual/SL-PlatformDifferences.html

对于 NDC 的 x,y 轴，全平台都是一致的：

屏幕从左到右为 x 轴的-1 到 1
屏幕从下到上为 y 轴的-1 到 1

对于 NDC 的 z 轴，即视图空间下的近平面到远平面的 z 轴：

在 OpenGL 平台：屏幕从前到后为 z 轴的-1 到 1
在 Direct3D 平台：屏幕从前到后为 z 轴的 1 到 0

如果是从相机中直接获取投影矩阵（Camera.projectionMatrix），Unity 始终返回 OpenGL 风格。但若想获取着色器中实际使用的矩阵，则需要调用GL.GetGPUProjectionMatrix，而该矩阵会随图形 API 不同而不同。

综上所述，投影矩阵在 Unity 中有多种实现方式，但考虑 Unity 的深度图是采用 Direct3D 风格存储的（包括那些解算深度图的函数），而且 Windows 平台更常用，故在此仅推导 Direct3D 风格的透视矩阵。

投影矩阵的构成

投影矩阵有两种类型：

"正交投影"（不实现近大远小）
"透视投影"（实现近大远小）。

其中透视投影比较特殊，本质上是"正交"和"透视"两种变换的复合矩阵：

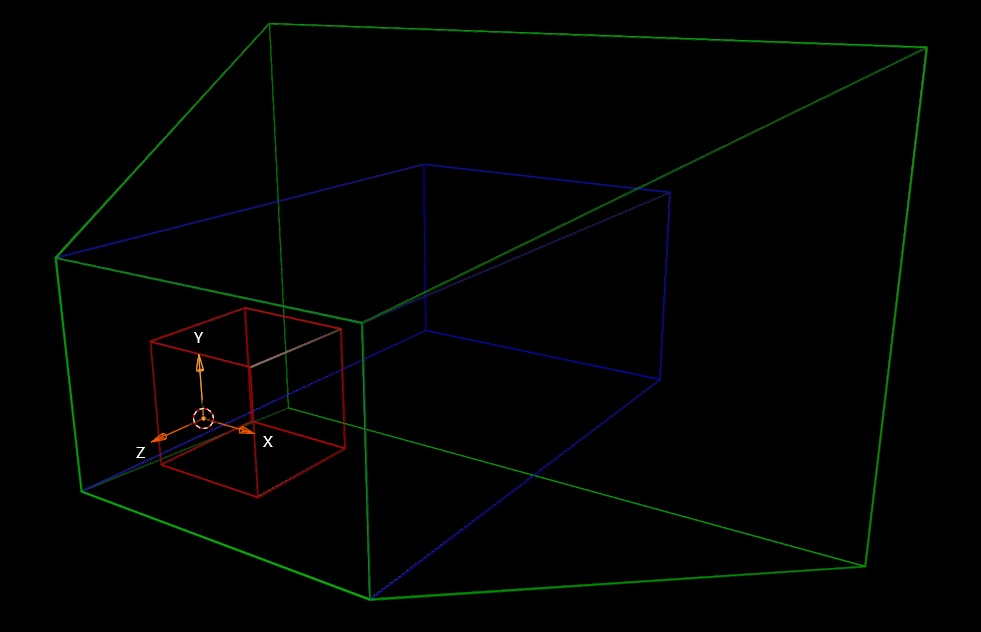
透视（上图绿框变蓝框）：将锥形的视野范围缩放成长方体。
正交（上图蓝框变红框）：将长方体的视野范围缩放到 NDC 空间（也是长方体）。

因此只需要学会透视投影，也就能学会正交投影，而且这样子理解起来会更简单。

正交变换（等价于正交投影矩阵）

正交投影矩阵由以下参数构成：

size：视锥体半高度。
aspect：宽高比（宽度/高度），用于得出半宽度。
near：近平面位置。
far：远平面位置。

由这些参数可以简单得出以下变量：

h：半高度（size）
w：半宽度（size*aspect）
n：近平面（near）
f：远平面（far）

正交投影矩阵是线性变换，所以可以直接通过直线公式（\(y=Ax+B\)）来拟合（如下图），具体而言是要实现以下映射：

\((-w,w)=>(-1,1)\)
\((-h,h)=>(-1,1)\)
\((-n,-f)=>(1,0)\)（受视图矩阵的 z 反转影响，故远近平面取反）

对于第一第二点，只要设置直线斜率（即对输入的 x,y 坐标直接除以 w,h 即可）。对于第三点则可以通过带入 z=-n 和 z=-f 两个线段端点成以下公式：

\(-An+B=1\)
\(-Af+B=0\)

进一步推导可得：

\( \begin{aligned} (-An+B)-(-Af+B) &= 1-0 \\ -An+B+Af-B &= 1 \\ Af-An &= 1 \\ A(f-n) &= 1 \\ A &= \frac{1}{f-n} \\ \end{aligned} \)

\( \begin{aligned} -(\frac{1}{f-n})f+B&=0\\ B &= \frac{f}{f-n}\\ \end{aligned} \)

最终根据上述结论，可用相关参数可构成正交投影矩阵：

\[\begin{bmatrix} \frac{1}{w} & 0 & 0 & 0 \\ 0 & \frac{1}{h} & 0 & 0 \\ 0 & 0 & \frac{1}{f-n} & \frac{f}{f-n} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} \]

透视变换（透视投影矩阵的一部分）

透视变换（后也称透视矩阵）的目的是实现近大远小，即根据 z 位置缩放 xy 轴，使任何位置的 x,y 都等于近平面的 x',y'（映射关系如下图）。

上图根据相似三角形定理可得对于 y 轴的透视变换如下公式：

\( \begin{aligned} \frac{y'}{n} &=\frac{y}{z} （n,z此处为长度，故不是负数）\\ y'&=\frac{yn}{z}\\ x'&=\frac{xn}{z}（x轴同理） \end{aligned} \)

现在要将上述公式反应在矩阵变换上：

对于 n，这是一个定值，直接利用缩放矩阵的原理就可以实现。
对于 z，这是一个变量，肯定无法直接写在矩阵中，但可以借助其次坐标 w 归一化的特性，将向量的 w （位置在 m43）设为 z 即可。

于是便可得出初步矩阵：

\( \begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ ? & ? & ? & ? \\ 0 & 0 & -1 & 0 \end{bmatrix} \)

注意因为视图矩阵中 z 被反转，此处为保证 xy 不受影响，因此需要将 m43 设置为 -1 来获取 +z。

此外 z 的系数都被标记为？，因为 z 也会受 w 归一的影响，而我们实际需要 z 保持不变，故需要对这些能对 z 产生作用的系数进行推导，以确保最终计算出的向量归一化前的 z 分量为\(-z^2\)（齐次坐标是实现除 z 而不是-z，所以为保持最终结果依然是视图空间的 -z ，z 分量应该是负数 z）。

由于前两个系数（m31,m32）是与 x,y 相乘，我们不需要所以始终为 0。而剩余的两个系数（m33,m34）设分别为 A,B 时，再加上视图空间向量（投影变换的输入向量）的 w 分量（B 的乘数）默认为 1，带入 z=-n 和 z=-f 两个特例后可得以下公式：

\(-An+B=-n^2\)
\(-Af+B=-f^2\)

推导可得：

\( \begin{aligned} (-An+B)-(-Af+B) &= (-n^2)-(-f^2) \\ -An+B+Af-B &= f^2-n^2 \\ Af-An &= (f-n)(f+n) \\ A(f-n) &= (f-n)(f+n) \\ A &= f+n \\ \end{aligned} \)

\( \begin{aligned} -(f+n)f+B&=-f^2\\ B &= -f^2+(f+n)f\\ B &= -f^2+f^2+nf\\ B &= nf\\ \end{aligned} \)

最终根据上述结论，可用相关参数可构成透视矩阵：

\[\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & f+n & nf \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \]

透视投影矩阵

将正交变换和透视变换的矩阵相结合可得如下矩阵：

\( \begin{aligned} &=\begin{bmatrix} \frac{1}{w} & 0 & 0 & 0 \\ 0 & \frac{1}{h} & 0 & 0 \\ 0 & 0 & \frac{1}{f-n} & \frac{f}{f-n} \\ 0 & 0 & 0 & 1 \\ \end{bmatrix} *\begin{bmatrix} n & 0 & 0 & 0 \\ 0 & n & 0 & 0 \\ 0 & 0 & f+n & nf \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}\\ &=\begin{bmatrix} \frac{n}{w} & 0 & 0 & 0 \\ 0 & \frac{n}{h} & 0 & 0 \\ 0 & 0 & \frac{f+n}{f-n}-\frac{f}{f-n} & \frac{nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix}\\ &=\begin{bmatrix} \frac{n}{w} & 0 & 0 & 0 \\ 0 & \frac{n}{h} & 0 & 0 \\ 0 & 0 & \frac{n}{f-n} & \frac{nf}{f-n} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \end{aligned} \)

在透视投影中，Unity 不直接提供 h（半高），需要利用 fov（视野角度）计算。利用三角函数可以轻松得出:

\( h = \tan(fov/2)*n\\ w = h * aspect \)

重新整理后可得最终透视投影矩阵：

\[\begin{bmatrix} \frac{1}{\tan(fov/2)*aspect} & 0 & 0 & 0 \\ 0 & \frac{1}{\tan(fov/2)} & 0 & 0 \\ 0 & 0 & \frac{near}{far-near} & \frac{near*far}{far-near} \\ 0 & 0 & -1 & 0 \\ \end{bmatrix} \]

线性深度推导

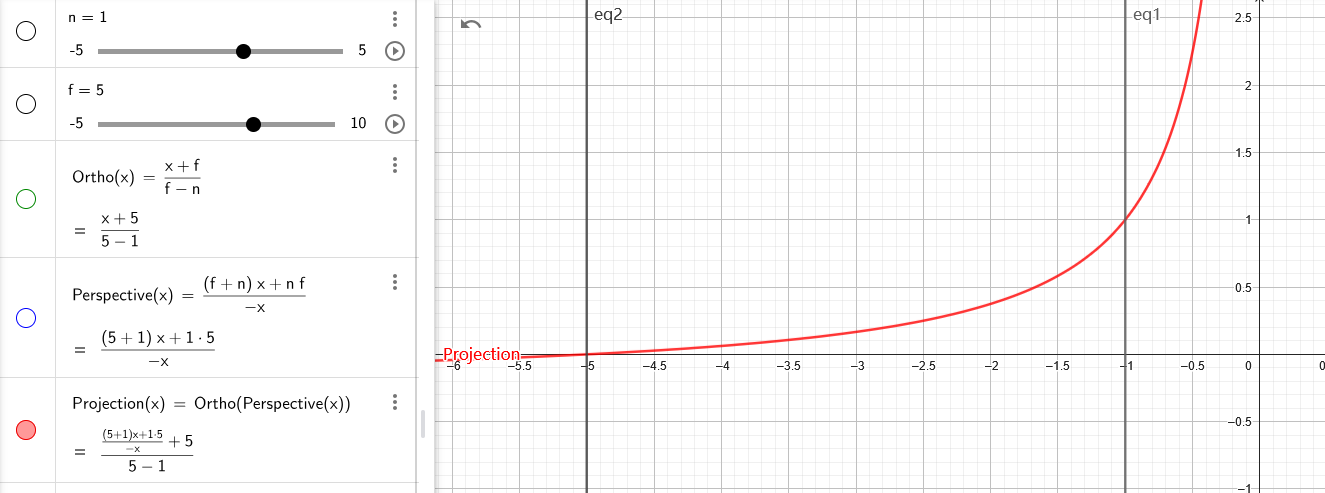
经过透视投影后得到的深度不是线性的（如上图），但很多特效实现都有利用 NDC 深度重建世界信息的需求，因此还需要研究一下如何逆推得到线性深度。

以下都是对 Unity 中相关线性深度求解函数的解析，利用下方链接可以查看每个函数的函数图，以便直观的感受深度变化效果：

https://www.geogebra.org/calculator/nxrfrkzj

LinearEyeDepth

将 NDC 中的深度反推为视图空间中的非反转深度（即原始的 z 轴坐标）。

该函数的实现可分成两个步骤，先执行 \(透视投影\) 的 \(逆函数\) 得出视图空间中的深度。由于视图空间中的深度为反转的 z 轴，故对该深度二次反转，以得到非反转深度。

即 \(LinearEyeDepth(z) = -逆透视投影(z)\)

根据之前的矩阵计算可得：

\( \begin{aligned} 透视投影 &= \frac{(\frac{nz}{f-n}+\frac{nf}{f-n})}{-z}\\ &=\frac{n(z+f)}{z(n-f)}\\ \end{aligned} \)
再对该函数求逆：

\( \begin{aligned} z'&=\frac{n(z+f)}{z(n-f)} \\ z(n-f)z'&=nz+nf\\ z(n-f)z'-nz&=nf\\ z((n-f)z'-n)&=nf\\ z&=\frac{nf}{(n-f)z'-n}\\ \end{aligned} \)

即：

\( 逆透视投影=\frac{nf}{(n-f)z-n} \)
加入反转，再简化：

\( \begin{aligned} &= -\frac{nf}{(n-f)z-n}\\ &= \frac{nf}{(f-n)z+n}\\ &= \frac{1}{\frac{f-n}{nf}z+\frac{1}{f}}\\ \end{aligned} \)

故最终结论为：

\[LinearEyeDepth(z)=\frac{1}{\frac{f-n}{nf}z+\frac{1}{f}} \]

Linear01Depth

将 NDC 中的深度反推为线性 0-1 深度（相机位置为 0，远平面为 1）。

很容易想到，只需要对 \(LinearEyeDepth\) 的结果除以远平面大小即可，即：

\( \begin{aligned} &= \frac{LinearEyeDepth(z)}{f}\\ &= \frac{1}{\frac{f-n}{nf}z+\frac{1}{f}} * \frac{1}{f}\\ &= \frac{1}{\frac{f-n}{n}z+1}\\ \end{aligned} \)

故最终结论为：

\[Linear01Depth(z)=\frac{1}{\frac{f-n}{n}z+1} \]

Linear01DepthFromNear

求解线性 0-1 深度（近平面为 0，远平面为 1）。（Unity 中的注释是这样写的，但实测根本不是）。

该函数的本质为：

\( \begin{aligned} &=Linear01Depth(z)*z\\ &=\frac{1}{\frac{f-n}{n}z+1}*z\\ &=\frac{1}{\frac{f-n}{n}+\frac{1}{z}}\\ \end{aligned} \)

其计算出的深度确实是线性，但近平面等于 \(Linear01Depth\)（z 等于 1，相乘后不变），远平面等于 0（z 等于 0，相乘后等于 0）。

若要实现真正的 \(Linear01DepthFromNear\) ，应对 \(逆透视投影函数\) 的结果直接进行 \(正交变换\)，然后调换深度为 0-1 方向，即：

\( \begin{aligned} &= 1 - 正交变换(逆透视投影(z))\\ &= 1-\frac{1}{f-n}LinearEyeDepth(z)+\frac{f}{f-n}\\ &= 1-\frac{1}{f-n}(\frac{nf}{(n-f)z-n}+f)\\ \end{aligned} \)