Efficient Scalable Multi-Party Private Set Intersection

论文学习：Efficient Scalable Multi-Party Private Set Intersection

这篇论文提出了一种基于双中心零共享（Bicentric Zero-Sharing）的高效、可扩展的MPSI协议及其变体，解决了现有方案在参与方数量、通信开销和抗共谋能力方面的局限性。

摘要

本文提出了一种基于**双中心零共享（Bicentric Zero-Sharing）**的高效可扩展多方隐私集合求交协议（MPSI）及其变体（如MPSI-CA和MTPSI）。通过将MPSI问题简化为两个中心参与者（Pivot与Leader）之间的两方PSI，我们实现了以下核心贡献：

• 双中心零共享的构建

提出一种基于不经意键值存储（OKVS） 的对称密钥操作方案，通过一轮共享与重构实现零共享。每个参与者的通信复杂度仅为O(n + m) ，且无需公钥操作。安全性依赖于Leader与Pivot不共谋 的假设，在半诚实模型下可抵抗任意其他参与者的共谋攻击，在随机预言机模型下可抵抗至多n−2个恶意客户端的攻击。

• 高效MPSI及变体协议

MPSI：通过结合双中心零共享与两方PSI协议，仅需Pivot和Leader执行两方PSI，其余客户端无额外操作。

MPSI-CA （交集基数计算）与MTPSI（阈值PSI）：通过调用两方PSI变体协议实现，例如基于DH-PSI-CA的实例化方案。

• 性能与可扩展性

实验表明，在15个参与者（各含2²⁰元素）的场景下，相比当前最优协议（Nevo等，CCS'21），我们的协议在局域网（LAN） 中提速46.4倍，在广域网（WAN） 中提速18.3倍，通信成本降低24.7倍。支持超大规模参与者：140个参与者 （各含2²⁰元素）时，MPSI与MPSI-CA在LAN中仅需4.557秒 与16.02秒。

引言

在安全多方计算（MPC）的众多功能中，多方隐私集合求交（MPSI）是实践需求最强烈的技术之一。在MPSI中，多个参与者各自持有数据集，他们希望在不泄露任何额外信息的前提下计算所有数据集的交集。

根据参与者数量，PSI可分为两方PSI和多方PSI（MPSI）。过去十年间，两方PSI技术发展迅速。基于向量不经意线性评估（VOLE）和不经意键值存储（OKVS）的协议速度已接近原始非安全哈希PSI。两方PSI可应用于隐私联系人发现、安全事件信息共享、密码安全检查等场景。例如，谷歌在2019年基于PSI推出"密码安全检查"插件，帮助用户验证密码安全性而不泄露隐私。此外，研究者还提出了PSI的多种变体，如PSI基数统计（PSI-CA）和阈值PSI（TPSI）。PSI-CA仅输出交集大小，可用于广告转化率测量；TPSI仅在交集大小超过预设阈值𝑟时输出结果，适用于生物特征认证、拼车应用等场景。

近年来，随着多方数据共享需求增加，MPSI及其变体（MPSI-CA、MTPSI）应用愈发广泛，适用于多方访问控制、匿名投票、共识机制等场景。2022年，MPSI变体被用于边缘计算的缓存共享，使多个网络运营商能在容量受限的共享缓存中存储高频访问的公共数据，同时保护数据集隐私。

从技术角度看，MPSI及其变体的设计需满足抗共谋攻击、避免部分参与者交集泄露、支持参与者规模扩展等要求，相比两方PSI更具挑战性。现有MPSI协议普遍存在两大局限：

• 计算效率低：多数协议要求核心参与者（甚至所有参与者）执行大量公钥操作；
• 通信复杂度高 ：核心参与者的通信复杂度达\(O(nm)\)，限制大规模应用；
• 功能扩展性不足：缺乏对MPSI-CA、MTPSI等变体的支持。

近期研究提出通过迭代将n方PSI简化为两方PSI的范式，仅使用对称密钥操作。但该协议易受参与者共谋攻击。

本文提出基于**双中心零共享（bicentric zero-sharing）**的新型MPSI协议，突破性体现在：

• 架构创新：通过OKVS共享与重构实现零共享，将MPSI简化为两方PSI；
• 效率提升 ：全流程仅使用对称密钥操作，单参与者通信复杂度降至\(O(n+m)\)；
• 安全增强 ：在半诚实模型下抵抗任意共谋（除Leader和Pivot外），在随机预言机模型下可抵御最多\(n-2\)个恶意客户端；
• 功能扩展：支持MPSI-CA和MTPSI等变体协议。

以及该协议特别适用于存在固定中心参与者的场景，例如：

• 电子选举：执政党领袖作为Leader，反对党领袖作为Pivot；
• 漏洞赏金：矿工（Pivot）发现的漏洞需经多方验证者（客户端）核验，并由赏金提供方（Leader）列示；
• 多方访问控制：企业联盟间的数据安全共享。

相关工作

表 1 综合对比了现有的 MPSI 协议，包括基于同态加密（HE）、混淆电路（GC） 和茫然传输（OT）的协议。由于与本文工作密切相关，我们重点关注 基于 OT 的 MPSI 协议。其他类别的 MPSI 协议主要依赖 HE 或 GC：

• 基于 HE 的协议：计算复杂度高，效率较低。
• 基于 GC 的协议：功能更强（支持对交集进行后续计算或负载处理），但同样受限于高计算成本。

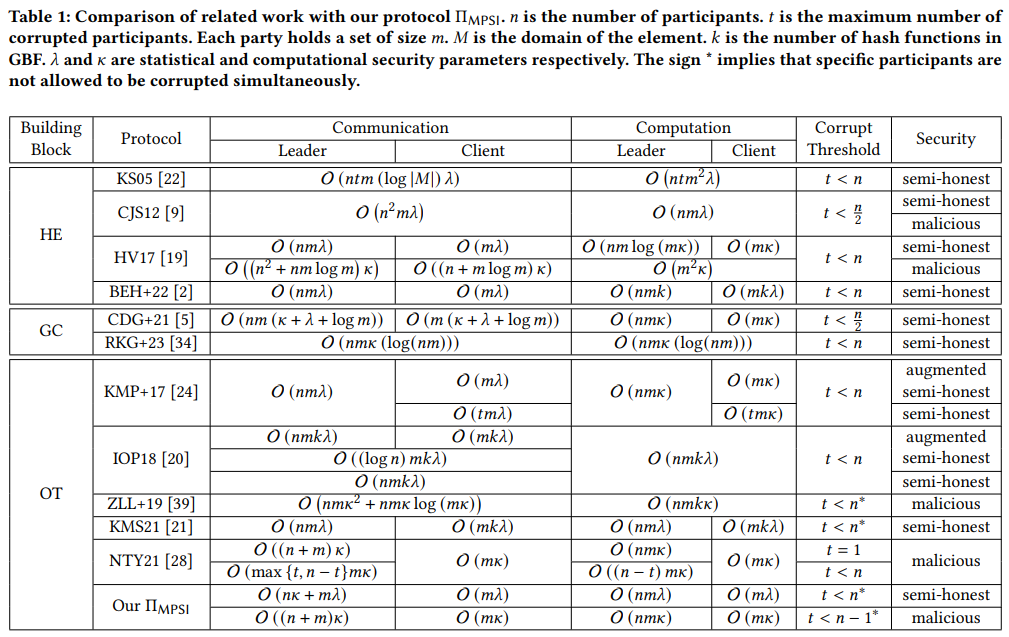
简单总结一下，现有 MPSI 协议在抗合谋、全局信息建模和扩展性方面面临挑战，而基于 OT 的协议通过优化拓扑与零共享机制逐步提升效率。本文提出的 双中心零共享（Bicentric Zero-Sharing） 进一步降低通信成本至 O(n+m)，并通过 Leader-Pivot 非合谋假设增强安全性。

技术概览

双中心零共享

将多方PSI（MPSI）简化为两方PSI的核心思想已被应用于\(x\)属于交集时，两个中心参与者所持的聚合值相等。我们将该思想抽象为双中心零共享（Bicentric Zero-Sharing）这一密码学原语。双中心零共享以各方私密集合为输入，最终向两个中心参与者分别返回一个值集，通过两方PSI计算交集。MPSI的结果可以直接从两方PSI结果中推导得出。

该思想源于\(x\)属于所有参与方的交集时，所有共享值的异或和为0。而在双中心零共享中，共享过程被集中到两个核心参与者------Pivot与Leader。类似地，仅当元素\(x\)属于所有参与方的交集时，Pivot与Leader所持共享值的异或和为0（即相等）时，两方持有的共享值才相等。

示例 ：假设四个参与者\(P_1-P_4\)（其中\(P_3\)为Pivot，\(P_4\)为Leader），其输入集分别为：

\(\begin{aligned}X_1 &= \{1,2,3,4,5\} \\X_2 &= \{1,3,4,5,6\} \\X_3 &= \{1,4,5,6,7\} \\X_4 &= \{1,5,6,7,8\}\end{aligned}\)

其交集为\(\{1,5\}\)。双中心零共享功能将分别生成随机值集合：

\(\begin{aligned}A &= \{56, 26, 73, 61, 10\} \\B &= \{56, 73, 30, 25, 35\}\end{aligned}\)

其中，对应的交集位置（元素1对应A的首位与B的首位，元素5对应A的第三位与B的第二位）实现了共享值的匹配。通过随后的两方PSI协议，Leader可从\(A \cap B = \{56,73\}\)反推出实际交集元素\(\{1,5\}\)。

双中心零共享构造（本文）

假设\(n\)个参与者\(P_1-P_n\)共同执行双中心零共享协议，其中：

\(P_1-P_{n-2}\)为普通客户端（Client）

\(P_{n-1}\)为Pivot

\(P_n\)为Leader

协议的核心是不经意键值存储（OKVS） 技术。OKVS包含编码（Encode）与解码(Decode)算法：

• Encode将键值对列表转换为数据结构\(S\)，具有"不经意性"------当所有值均匀随机时，\(S\)不泄露任何键信息。
• Decode可对任意键解码输出值（若键存在于编码阶段则输出原值，否则输出随机值）。关键特性：若\(S = S_1 \oplus \cdots \oplus S_{n-1}\)，则解码满足线性可加性，即 \(\textsf{Decode}(S,k) = \bigoplus_{i=1}^{n-1} \textsf{Decode}(S_i,k)\)

协议执行步骤：

• Leader初始化 ： Leader\(P_n\)将自己集合\(X_n\)的每个元素\(x_n^j\)与伪随机值\(b^j = \textsf{PRF}_k(x_n^j)\)绑定，生成OKVS对象\(S = \textsf{Encode}(\{(x_n^j,b^j)\})\)。
• 共享S ： 将\(S\)拆分为\(S = S_1 \oplus \cdots \oplus S_{n-1}\)。\(S_1,...,S_{n-2}\)通过伪随机生成器（PRG）生成种子分发，让各Client本地生成；最后计算\(S_{n-1} = S \oplus S_1 \oplus \cdots \oplus S_{n-2}\)。
• 双方向Pivot提交 ： 各个Client\(P_i\)用\(X_i\)的元素解码自己的\(S_i\)，获得临时值集\(\{y_i^j\}\)。为避免直接发送\((x_i^j,y_i^j)\)泄露原始数据，Client需再次编码为OKVS对象\(T_i = \textsf{Encode}(\{(x_i^j,y_i^j\})\)后发送给Pivot。
• Pivot计算最终共享值 ： Pivot\(P_{n-1}\)将自己的集合\(X_{n-1}\)中各元素\(x_{n-1}^j\)代入各个Client发来的OKVS对象进行解码，累加所有解码结果并与自有共享分量\(S_{n-1}\)的解码值异或，得到最终共享值集\(A\)。当且仅当元素\(x\)属于全局交集时，根据OKVS线性性质，\(a^j = b^{j'}\)。

该构造仅使用对称密钥操作（PRF、PRG、OKVS编码/解码），每个参与方的通信复杂度为\(O(n + m)\)，显著优于依赖公钥操作（如OT/VOLE）的现有方案。

安全假设：

协议安全性建立在Leader与Pivot不共谋的前提下。这符合实际中两种角色可能代表利益冲突方的场景（如：执政党与反对党领袖、漏洞披露中的矿工与验证者等）。在此模型下：

• 半诚实模型中可抵抗除Leader和Pivot外任意数量的共谋
• 恶意模型中可抵抗至多 \(n-2\)个恶意Client的攻击

多方PSI及其变种协议

基于双中心零共享的MPSI：Pivot与Leader只需执行标准两方PSI协议。

扩展功能：

• MPSI-CA（交集基数）：基于的DH-PSI-CA协议，使双方仅交互获得交集大小
• MTPSI （门限PSI）：引入阈值\(r\)，仅当交集大小超过\(r\)时揭示结果

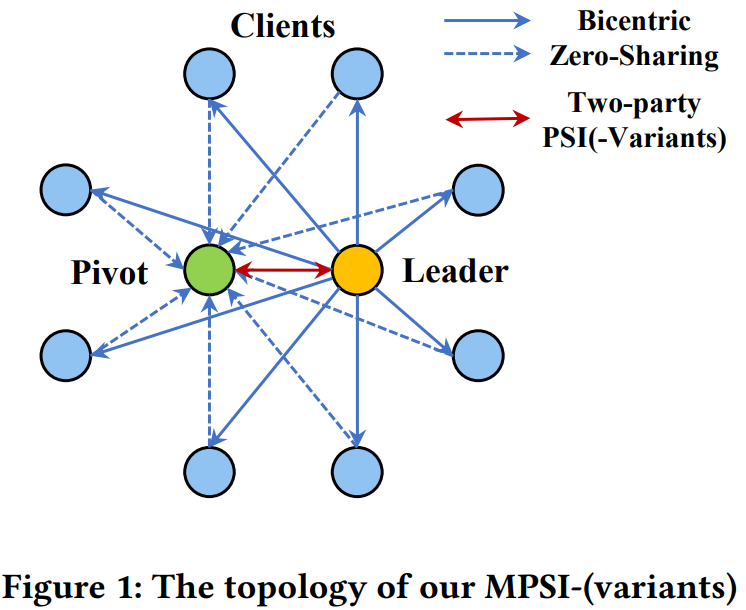
协议拓扑结构为星型 ：Clients仅参与零共享阶段，后续计算仅需Leader与Pivot交互（如图1所示）。这种设计极大提升了协议的可扩展性，即使参与者数量超过百个仍能高效运行。实验表明，在15方各含\(2^{20}\)元素的场景下，本方案相比现有最优（CCS'21）在局域网(WAN)环境下提速46.4倍、广域网(WAN)提速18.3倍，通信开销减少24.7倍，且随着参与方数量增加优势更显著。

文本贡献

双中心零共享（第3节）

我们从现有的多方隐私集合求交（MPSI）工作中抽象出一个称为双中心零共享（Bicentric zero\(O(n+m)\)。我们证明，在Pivot（支点）与Leader（领导者）不同时腐败的半诚实模型中，该构造对任意腐败阈值 \(t < n\)的安全性 。进一步地，在随机预言机模型下，该方案甚至可以抵抗\(t < n-1\)参与者的恶意腐败行为。相较而言，[28]第3节所提的实现方案中，若任一方中心参与方（支点或领导者）与其他客户联合腐败，其安全性即被破坏------而我们的构造在效率与安全性上均优于现有工作。

MPSI及其变体（第4节）

基于双中心零共享与双向PSI协议，我们提出了一种新型MPSI协议。该协议继承了双中心零共享的安全特性，且在完成零共享阶段后，仅需支点与领导者执行双向PSI，而所有客户无需额外操作。因此，我们的MPSI协议在效率与支持大规模参与方扩展性上表现卓越。同时，我们将双中心零共享与双向PSI变体（如仅输出交集大小的PSI-CA、阈值条件TPSI等）相结合，实现了相应的MPSI变体协议，包括仅输出交集规模的MPSI-CA和满足阈值条件才输出交集的MTPSI。我们以DH-PSI-CA为基础，具体实现了MPSI-CA协议的实例。

实验评估（第5节）

我们完整实现了双中心零共享、MPSI及MPSI\(2^{20}\)元素的场景下，我们的MPSI协议在局域网（LAN）环境中提速46.4倍、广域网（WAN）环境中提速18.3倍，且通信开销降低24.7倍。随着参与方数量与数据规模增长，这一优势更显著。据我们所知，这是首个支持超百参与方（达140方）的MPSI协议------在该规模下，MPSI与MPSI-CA协议在LAN环境仅需4.557秒与16.02秒即可完成计算。代码实现已在GitHub开源：https://github.com/orzcy/BZS-MPSI。

预备知识

符号说明

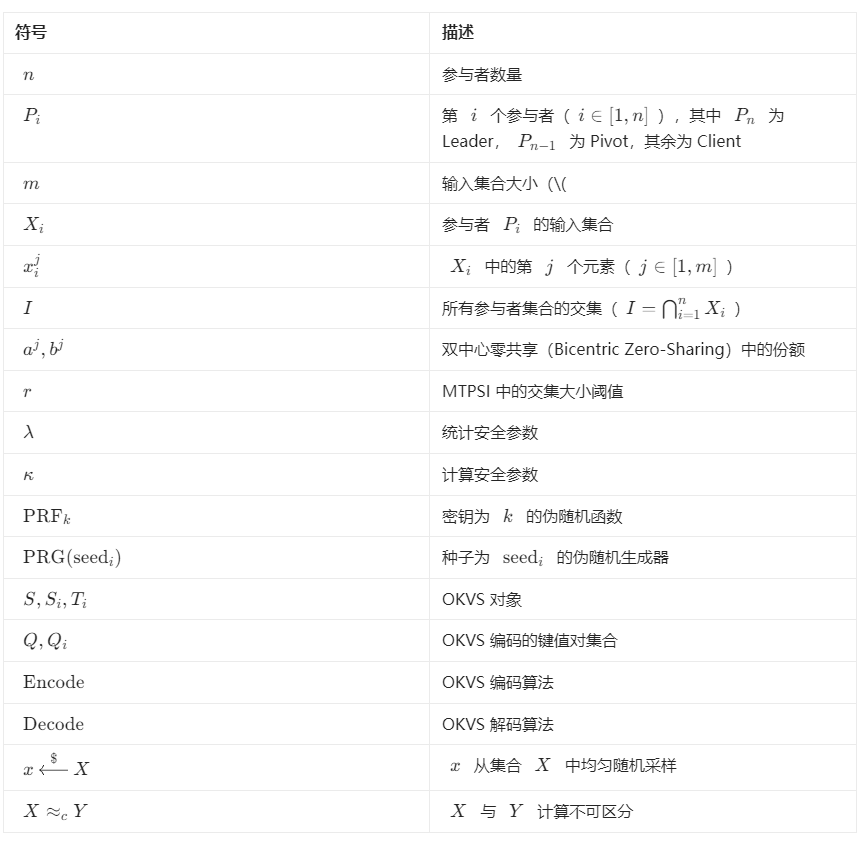
PSI及变体

在 \(n\)\(P_i\)持有私有集合 ，目标是计算所有集合的交集 \(I\)，且不泄露额外信息。最终结果 \(I\)由 Leader \(P_n\) 获得。其理想功能如图2所示。

PSI变体：

1. PSI\(|I|\)，理想功能如图3。
2. TPSI（阈值PSI）：仅当交集大小超过预设阈值 \(r\)时输出交集，否则输出 \(\bot\)，理想功能如图4。

OKVS

OKVS 是一种可编码键值对的数据结构，同时隐藏键的集合。其核心算法包括：

• Encode ：输入键值对集合 \(Q \subseteq (\mathcal{K} \times \mathcal{V})^m\)，生成数据结构 \(S\)。

• Decode ：输入 \(S\)和键 \(k \in \mathcal{K}\)，输出值 \(v \in \mathcal{V}\)。

关键性质：

1. 正确性 ：若 \((k, v) \in Q\)，则 \(\text{Decode}(S, k) = v\)。
2. 不经意性 ：若所有 \(v_i\) 是均匀随机的，则 \(S\) 不泄露任何关于 \(k_i\)的信息。
3. 线性性 ：若 \(S = S_1 \oplus S_2 \oplus \cdots \oplus S_{n-1}\)，则 \(\text{Decode}(S, k) = \bigoplus_{i=1}^{n-1} \text{Decode}(S_i, k)\)。

安全模型

• 半诚实模型：敌手严格遵循协议，但试图通过消息记录和内部状态推断额外信息。
• 恶意模型：敌手可任意偏离协议执行。

安全性定义：

1. 半诚实安全性 ：存在模拟器 \(\text{Sim}\)，使得真实视图与理想视图计算不可区分（公式3）。
2. 恶意安全性：对于任意恶意敌手，存在理想模型中的模拟器，使得真实执行与理想执行不可区分（公式4）。

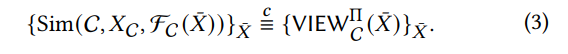
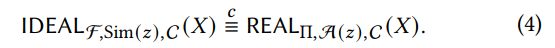
双中心零共享

我们的多方PSI方法主要构建在双中心零共享（Bicentric Zero）\(P_i(i \in [1,n])\)输入包含 \(m\)个元素的私有集合 \(X_i = \{x_i^1, ..., x_i^m\}\)。协议运行后，枢纽节点 \(P_{n-1}\)将获得包含 \(m\)个随机值的集合 \(A = \{a^1, ..., a^m\}\)，领导者节点\(P_n\) 则获得另一包含 \(m\) 个随机值的集合 \(B = \{b^1, ..., b^m\}\)。其中，\(a^j = b^{j'}\)当且仅当 \(x_{n-1}^j = x_n^{j'} \in \bigcap_{i=1}^n X_i\)。这一过程的理想功能如图5所示。需要注意的是，在半诚实模型中，敌手始终设定位 \(\text{abort}=0\)。本节将构建在半诚实模型下实现该理想功能的具体协议 \(\Pi_{\mathrm{BZS}}^{n,m}\) 和恶意模型下的增强协议 \(\Pi_{\mathrm{BZS}^*}^{n,m}\)。

具体协议

步骤1：领导者节点初始化

领导者 \(P_n\)为自身每个元素 \(x_n^j\)生成伪随机值 \(b^j = \text{PRF}k(x_n^j)\)，并构建OKVS结构 \(S = \text{Encode}(\{(x_n^j, b^j)\})\)。随后，将 \(S\) 分解为 \(S = S_1 \oplus \cdots \oplus S{n-1}\)，其中 \(S_1, ..., S_{n-2}\)使用伪随机生成器（PRG）生成种子分发至对应客户端，而 \(S_{n-1} = S \oplus S_1 \oplus \cdots \oplus S_{n-2}\) 交予枢纽节点。

步骤2：客户端处理

客户端 \(P_1, ..., P_{n-2}\)接收 \(S_i\)后，对自身集合的每个元素 \(x_i^j\)计算 \(y_i^j = \text{Decode}(S_i, x_i^j)\)。为防止泄露元素信息，客户端进一步构建新的OKVS结构 \(T_i = \text{Encode}(\{(x_i^j, y_i^j)\})\)发送至枢纽节点。

步骤3：枢纽节点整合

枢纽节点 \(P_{n-1}\)收集所有 \(T_i\)后，对自身每个元素 \(x_{n-1}^j\) 计算： \(a^j = \bigoplus_{i=1}^{n-2} \text{Decode}(T_i, x_{n-1}^j) \oplus \text{Decode}(S_{n-1}, x_{n-1}^j)\)

根据OKVS的线性特性，若 \(x_{n-1}^j\)存在于所有参与者的集合交集中，则 \(a^j\) 将与领导者生成的对应 \(b^{j'}\) 相等。

基于双中心零共享的MPSI协议

通过双中心零共享（Bicentric Zero-Sharing），协议将多方PSI简化为两方PSI。仅需选取"枢纽方"（Pivot）和"领导方"（Leader）执行最终的两方PSI，其余客户端（Clients）仅参与密钥共享过程。具体步骤包括：

领导方生成并分拆共享密钥（OKVS结构），通过线性解码属性确保交集元素的密钥匹配。

客户端对本地元素加密生成中间值，枢纽方汇总中间值构造最终共享。

枢纽方与领导方执行两方PSI（如基于VOLE的高效协议）获取交集结果。

MPSI变体

MPSI-CA（交集基数计算）：在两方PSI阶段替换为基数协议（如Diffie-Hellman基数统计），仅输出交集元素数量。

MTPSI（阈值PSI）：添加阈值条件判断，仅当交集大小超过预设值时输出结果。

安全性分析

半诚实模型

抗合谋假设 ：协议的安全性基于领导者与枢纽节点不合谋的前提。在此条件下，即使其余客户端任意合谋也无法推断出交集外的元素信息。

可证安全 ：通过现实\(t < n\) 的腐败阈值。

恶意模型增强

随机预言机（RO）保障 ：引入哈希函数作为RO，客户端需在发送 \(T_i\)前对元素进行哈希承诺。枢纽节点验证承诺一致性，可抵抗至多 \(n-2\)个恶意客户端的攻击。

错误检测：若客户端提供不一致的OKVS结构，枢纽节点可通过解码失败识别恶意行为并终止协议。

性能分析

与现有方案相比，本协议通过以下创新显著提升效率：

• 对称密钥操作主导 ：避免公钥运算，客户端计算复杂度仅 \(O(m)\)
• 通信优化 ：客户端通信量从传统 \(O(nm)\) 降至 \(O(n + m)\)，枢纽与领导者仅需执行最终的两方PSI
• 超大规模支持 ：实验显示协议可支持超100方参与（如140方，每方 \(2^{20}\)元素），LAN环境下MPSI仅需4.557秒。

通过将多方PSI拆解为高效的双中心零共享与两方PSI的组合，本工作为大规模隐私计算提供了兼具效率与安全性的新范式。

实验过程

实验目标

验证基于双中心零共享（Bicentric Zero-Sharing）的MPSI协议及其变体（如MPSI-CA、MTPSI）的效率和可扩展性。

与现有最先进的MPSI协议（如Nevo等人在CCS'21提出的协议）进行性能对比。

实验环境

• 网络设置：分为局域网（LAN，低延迟）和广域网（WAN，高延迟）两种场景。
• 数据集规模 ：每个参与者的集合大小为 \(2^{20}\)（约100万元素）。
• 参与者数量：测试覆盖15至140个参与者，验证协议的可扩展性。

实验结果

效率对比

• 15参与者场景 （每个集合含 \(2^{20}\)元素）：
• LAN环境 ：协议速度提升 46.4倍。
• WAN环境 ：协议速度提升 18.3倍。
• 通信成本 ：减少 24.7倍。
• 可扩展性 ：随着参与者数量增加，性能优势更加显著。例如：
  • 140参与者场景 （每个集合含 \(2^{20}\)元素）：
  • MPSI协议 ：仅需 4.557秒（LAN）。
  • MPSI-CA协议 ：仅需 16.02秒（LAN）。

技术优势

• 对称密钥操作：协议主要依赖对称加密操作，避免了公钥计算的高开销。
• 通信复杂度 ：每个参与者的通信复杂度为 \(O(n + m)\)，显著优于现有协议的 \(O(nm)\)。
• 抗合谋性 ：在非合谋假设下（Leader与Pivot不勾结），协议在半诚实模型中可抵抗任意合谋攻击，在恶意模型中可抵抗最多 \(n-2\) 个恶意客户端。

实验表明，基于双中心零共享的协议在效率、通信成本和可扩展性上均显著优于现有方案，尤其适用于大规模多方隐私计算场景（如电子投票、边缘计算缓存共享）。

总结

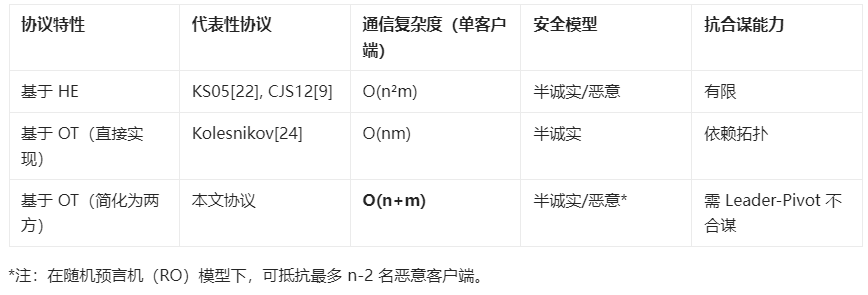
与现有工作的对比：