Floyd算法------全源最短路
cerr:标准输出错误流:不会输出到freopen制定的out文件中,而是会输出到错误文件中。
提交上去无论加不加freopen,哪怕是提交到洛谷,也只是比较out文件中的值,而不会管cerr输出的东西
好处:调试的时候用cerr,哪怕忘删调试调试
例题1:传递闭包
floyd可以直接算,但复杂度太高
压缩:用bitset优化
bool:00000001/00000000
bitset:1/0
bool&bool运算时间:O(n)
bitset&bitset:O(n/w)(w是机器字长,一般考试是64,即优化速度快了64倍)
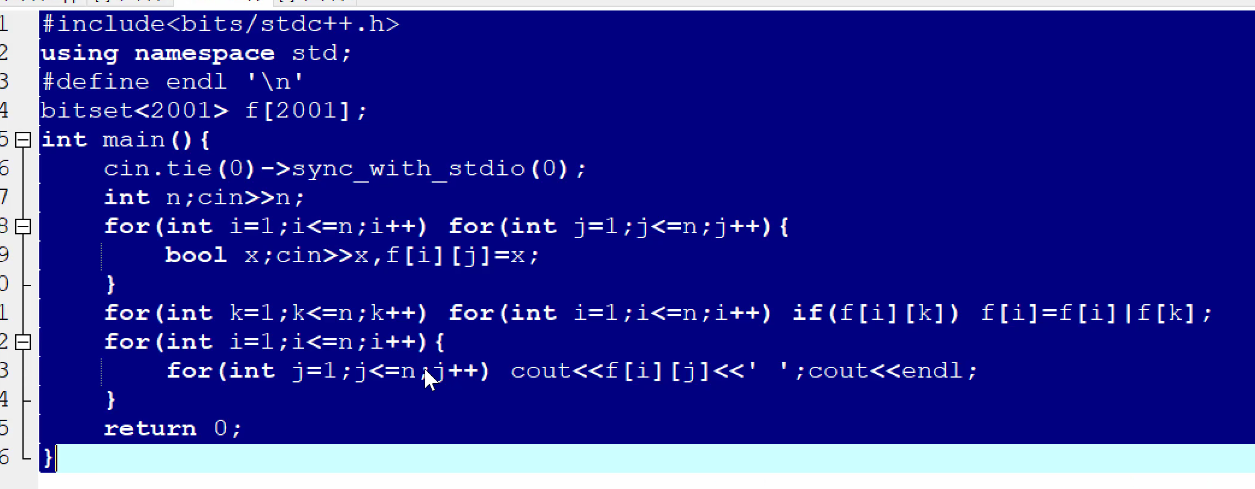
这里看一下这的算法:
假设有一条1-2-3-4的链
f[1]=1100,即能到达12点,到不了34
1:1100 由于这里1能够到达2if(f[i][k])成立,才能用2去更新1的所有可达点
2:1110
1:1110
3:0111
1:1111
这样经过两轮更新,就能到34了
(p.s:其实实际上不是逮着一个点一直更新它,这样可能有更新不到的情况。实际上是先用一个点去更新所有可达点(先枚举k))
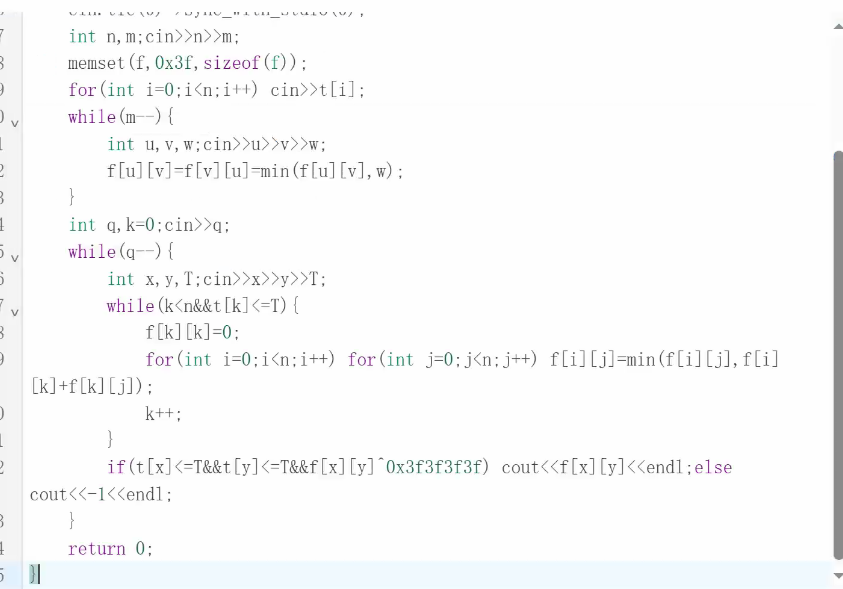
例题二:灾后重建
方法一:把所有讯问离线下来,按照t升序进行回答,在排回去
但是这道题保证了Q次讯问的t是不降的,所以就不用离线下来排序了
而且村庄标号越大,解封时间越晚
所以直接枚举点的标号就是解封顺序
用k来代表目前解封到第几个点了
当k<n时(总共就n个点,想干啥)并且k这个点解封的时间早于讯问时间(那么在它之前所有点都解封了)
那么以新解封的k这个点作为中转点,对所有之前的点进行更新
然后再向后探索一个点,知道新的点不存在或未解封
如果讯问的时间中k已经跑过一遍,就不用再跑一遍,直接用这张最后更新的图输出结果就行
输出时要特判:1.起点终点是否尚未解冻2.起点终点之间是否有连线
例题3:无向图的最小问题
假设这个环上就三个点,那么环得长度就是三个点之间的最短路径和
先跑Floyd
假设这三个顶点分别是ijk,那么最短环就是ij+ik+jk之间的最短路
但是一个例子:1-2-3链
很明显:没有环
但是Floyd会将1-3之间强制加上一条长度为1-2+2-3的边
这样程序就会算出最小环位1-2-3-2-1,很明显,有重边,肯定不行
怎么解决?
既然Floyd会强制改变边,那么我们就把边提前备份出来一边,不让Floyd动不就好啦
等用完了再让Floyd动也不迟
代码中mp表示打死不动,我们备份出来的原边长
f代表我们已经用完了,让Floyd去算完的边长
我们先固定下来一个点k,是这个环路径上经过的所有点中编号最大的那个
再枚举两个互不相同的点ij且比k小
kij的环必须是k到i、j的直接路径+i、j之间的最短路径长度
枚举完所有符合条件的环之后,要以k为中转点对所有点更新f数组
因为k以后再也不可能是k了,只能作为最短路径上的中转点
新的一轮ijk,ki、kj都是mp用的直接距离不会有影响
而ij之间的f数组求的是以所有比k小的的点为中转点的最短路
换句话说,ij这条边你就算走出花来,也不可能经过k点或比k更大的点
这样就可以完美地列举所有环了


(倒数第三行的INT_MAX改为1e8)
例题四:Redistributing Gifts S
把最优性转换成可行性问题,用传递闭包解决
建图,如果u看得上v的礼物,觉得v的礼物比他的好,那么就建一条边u->v
然后先跑一遍传递闭包,求出所有可达点
如果i可以到达j点,那么说明i可以拿到j的礼物
最后就输出每一个奶牛,如果它能拿到愿望清单上的1号礼物,就输出1号(不一定就是礼物1,只是排名最靠前的那个)
如果能,就输出完了broke掉,否则就下一个,直到找到最靠前的(肯定能找到的,毕竟自己到自己要设为可达)
代码吗......嘿嘿,手速慢没截到,要不那个时候的我(不会吧?我的博文还有除我以外的人看?)再补上?嘻嘻......反正坑是填不完的嘛