注:本文为 "等精度测频:FPGA 应用与实现" 相关文章合辑。
图片清晰度限于引文原状。
如有内容异常,请看原文。
等精度测频的原理和基于 FPGA 的实现
216549856 于 2025-01-13 11:30:17 发布
我们通过 FPGA 测量信号频率,一般来说有两种方案:传统测频法和等精度测频法。
方案一:传统测频法
传统测频是在一段闸门时间内直接对输入信号的周期进行计数,也被叫做直接测频法。设闸门信号为 gate,检测待测信号上升沿,然后判断 gate 是否为高电平,若为高电平便开始计数。这就存在 gate 的时间和待测信号周期数可能不成整数倍,导致产生 ±1 Hz 的误差。
方案二:等精度测频法
等精度测频可以弥补传统测频的缺点,它保证了闸门时间永远是被测信号周期的整数倍。设预设闸门信号为 base,实际闸门信号为 gate,检测待测信号上升沿,当 base 为高电平时,实际闸门打开,gate 为高电平,此时两个计数器同时对标准信号和待测信号的周期进行计数。当 base 为低电平时,实际闸门关闭,gate 为低电平,计数器停止计数。下面的时序图可以很好地说明(从别人博客摘过来的,但他博客里说图是从百度摘过来的,原博客看水印):
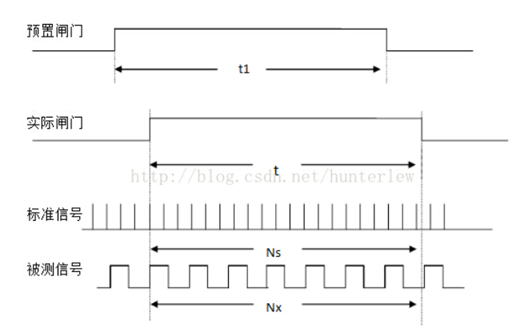
最终由公式:
待测信号频率 待测信号实际闸门周期数 = 标准信号频率 标准信号实际闸门周期数 \frac{\text{待测信号频率}}{\text{待测信号实际闸门周期数}} = \frac{\text{标准信号频率}}{\text{标准信号实际闸门周期数}} 待测信号实际闸门周期数待测信号频率=标准信号实际闸门周期数标准信号频率
可以得到待测信号的频率。
结论
由等精度测量公式可以知道等精度测频的误差来源于标准信号,而标准信号的频率为 50 MHz,可以认为误差足够小,所以可以消除 ±1 Hz 的误差。并且因为等精度测频能够在整个时域保持恒定的误差,所以非常适合用来测量可调位同步时钟信号的频率。
vhdl
module FreMeasure(
input clk,
input rst_n,
input Sig_in,
output reg [31:0] Fre
);
parameter T_1s = 28'd49_999_999;
//------------------------------------------------------------------------
// 预置闸门
reg [27:0] TCount;
always @ (posedge clk or negedge rst_n)
if(!rst_n)
TCount <= 28'd0;
else if(TCount >= T_1s)
TCount <= 'd0;
else
TCount <= TCount + 1'b1;
reg TCountCnt;
always @ (posedge clk or negedge rst_n)
if(!rst_n)
TCountCnt <= 1'b0;
else if(TCount >= T_1s)
TCountCnt <= ~TCountCnt;
//------------------------------------------------------------------------
// 实际闸门
reg startCnt;
always @ (posedge Sig_in)
if(TCountCnt == 1'b1)
startCnt <= 1'b1;
else
startCnt <= 1'b0;
//------------------------------------------------------------------------
// 在实际闸门中计数
reg [31:0] SigTemp;
always @ (negedge Sig_in)
if(startCnt == 1'b1)
SigTemp <= SigTemp + 1'b1;
else
SigTemp <= 'd0;
//------------------------------------------------------------------------
// 锁存输出
always @ (negedge startCnt)
Fre <= SigTemp;
endmoduleFPGA 频率计实验
耐心的小黑 于 2020-11-01 11:27:44 发布
参考:正点原子开拓者 FPGA 开发指南
数字频率计是一种基本的测量仪器,被广泛应用于航天、电子、测控等领域。基于传统测频原理的频率计的测量精度将随被测信号频率的下降而降低,在使用中有较大的局限性,而等精度频率计不但具有较高的测量精度,而且在整个频率区域能保持恒定的测试精度。
一、等精度频率计简介
频率测量在电子设计和测量领域中经常用到,因此对频率测量方法的研究在实际工程应用中具有重要意义。常用的频率测量方法有两种:周期测量法 和 频率测量法。
- 周期测量法是先测量出被测信号的周期 T T T,然后根据频率 f = 1 T f = \frac{1}{T} f=T1 求出被测信号的频率。
- 频率测量法是在时间 t t t 内对被测信号的脉冲数 N N N 进行计数,然后求出单位时间内的脉冲数,即为被测信号的频率。
但是上述两种方法都会产生 ±1 个被测脉冲的误差,在实际应用中有一定的局限性。根据测量原理,很容易发现周期测量法适合于低频信号测量,频率测量法适合于高频信号测量(因为周期越大或者频率越高,那么所测得的周期或者脉冲数 N N N 的相对误差就会越小),但二者都不能兼顾高低频率同样精度的测量要求。
等精度测量的一个最大特点是测量的实际门控时间不是一个固定值,而是一个与被测信号有关的值,刚好是被测信号的整数倍 。在计数允许时间内,同时对基准时钟和被测信号进行计数,再通过数学公式推导得到被测信号的频率。由于门控信号是被测信号的整数倍,就消除了对被测信号产生的 ±1 周期误差,但是会产生对基准时钟 ±1 周期的误差。等精度测量原理如下图所示:

从以上叙述的等精度的测量原理可以很容易得出如下结论:首先,被测信号频率 clk_fx 的相对误差与被测信号的频率无关;其次,增大测量时间段"软件闸门"或提高"标频" clk_fs,可以减小相对误差,提高测量精度;最后,由于一般提供基准时钟 clk_fs 的石英晶振稳定性很高,所以基准时钟的相对误差很小,可忽略 。假设基准时钟的频率为 100 MHz,只要实际闸门时间大于或等于 1 s,就可使测量的最大相对误差小于或等于 1 0 − 8 10^{-8} 10−8,即精度达到 1 100 MHz \frac{1}{100 \text{MHz}} 100MHz1。等精度测量的核心思想在于如何保证在实际测量门闸内被测信号为整数个周期,这就需要在设计中让实际测量门闸信号与被测信号建立一定的关系。基于这种思想,设计中以被测信号的上升沿作为开启门闸和关闭门闸的驱动信号,只有在被测信号的上升沿才将上图中预置的"软件闸门"的状态锁存,因此在"实际闸门" T x T_x Tx 内被测信号的个数就能保证整数个周期,这样就避免普通测量方法中被测信号的 ±1 的误差,但会产生高频的基准时钟信号的 ±1 周期误差,由于基准时钟频率远高于被测信号,因此它产生的 ±1 周期误差对测量精度的影响十分有限,特别是在中低频测量的时候,相较于传统的频率测量和周期测量方法,可以大大提高测量精度。
等精度测频的原理图如下图所示。图中,预置软件闸门信号 GATE 是由 FPGA 的定时模块产生,GATE 的时间宽度对测频精度的影响较小,故可以在较大的范围内选择,GATE 信号经被测时钟 clk_fx 同步化(图中的 D 触发器)到被测时钟域下。另外,为了方便处理,这里选择预置闸门信号的长度由参数 GATE_TIME 设置。图中的 fs_cnt 和 fx_cnt 是 2 个可控的 32 位高速计数器,fs_cnt_en 和 fx_cnt_en 分别是其计数使能端,由同步化后的 GATE 信号控制,基准时钟信号 clk_fs 从时钟输入端 clk_fs 输入,待测信号 clk_fx 从时钟输入端 clk_fx 输入。测量时,生成的 GATE 信号,在被测时钟同步化后用来控制启动和关闭 2 个计数器,2 个计数器分别对被测信号和基准时钟计数。若在一次实际闸门时间 GATE_TIME 中,计数器对被测信号的计数值为 fx_cnt,对基准时钟的计数值为 fs_cnt,而基准时钟的频率为 CLK_FS,则被测信号的频率为 clk_fx,则由公式:
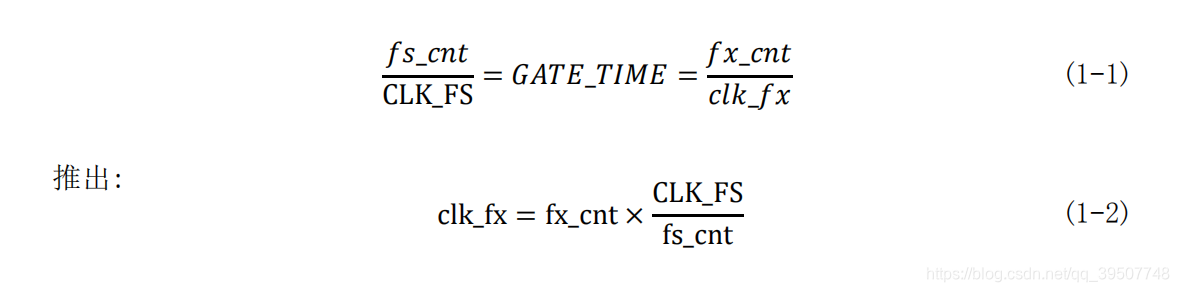
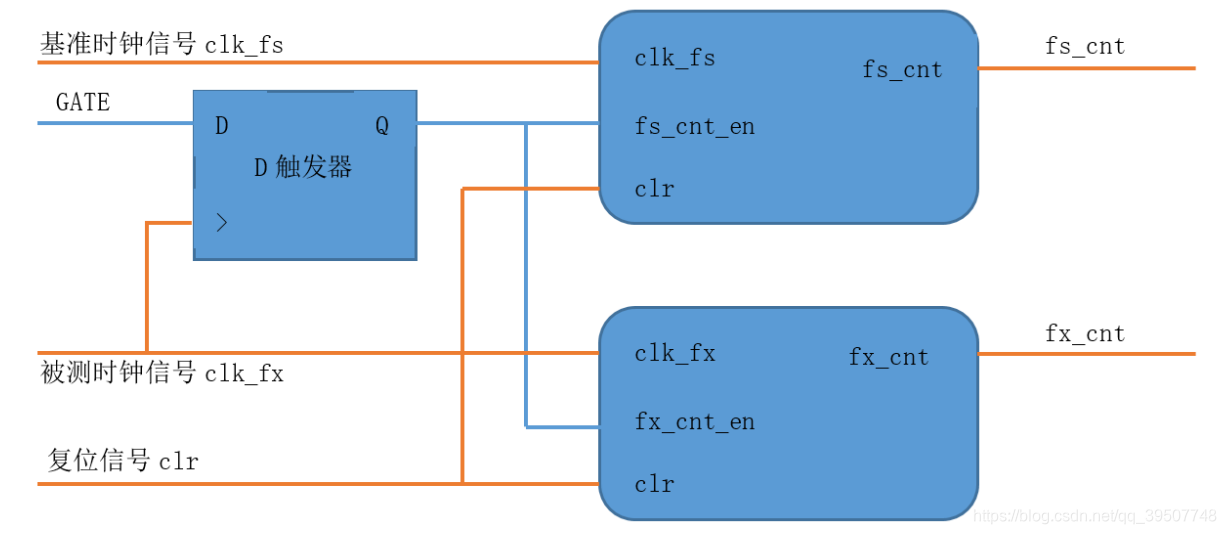
二、实验任务
板载 50 MHz 的时钟通过分频产生某一频率的时钟信号,作为被测时钟,然后用 Verilog HDL 编写的等精度测量模块测量被测时钟,并通过数码管显示。
三、程序设计
根据实验任务,我们可以大致规划出系统的控制流程:首先我们设计一个测试时钟模块用于生成被测的时钟,然后用等精度频率计模块测量被测时钟的频率,并将测得的时钟频率值送入数码管显示模块进行显示。由此画出系统的功能框图如下所示:
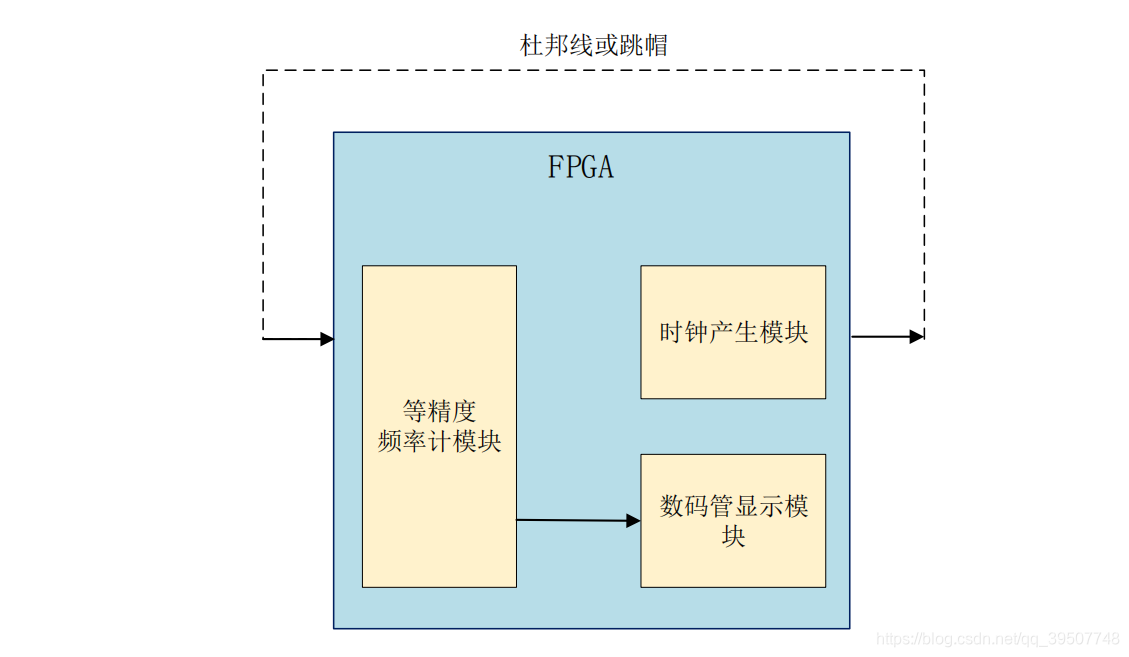
由系统框图可知,FPGA 部分包括四个模块:顶层模块(top_cymometer)、等精度频率计模块(cymometer)、时钟产生模块(clk_test)、以及数码管显示模块(seg_led)。各模块功能如下:
顶层模块(top_cymometer)
顶层模块完成了对其它三个模块的例化,实现各模块之间的数据交互。时钟产生模块产生被测时钟输出,并从外部接入至等精度频率计模块,以进行频率测量,将测量的结果传输给数码管驱动模块进行显示。顶层模块的原理图如下图所示:
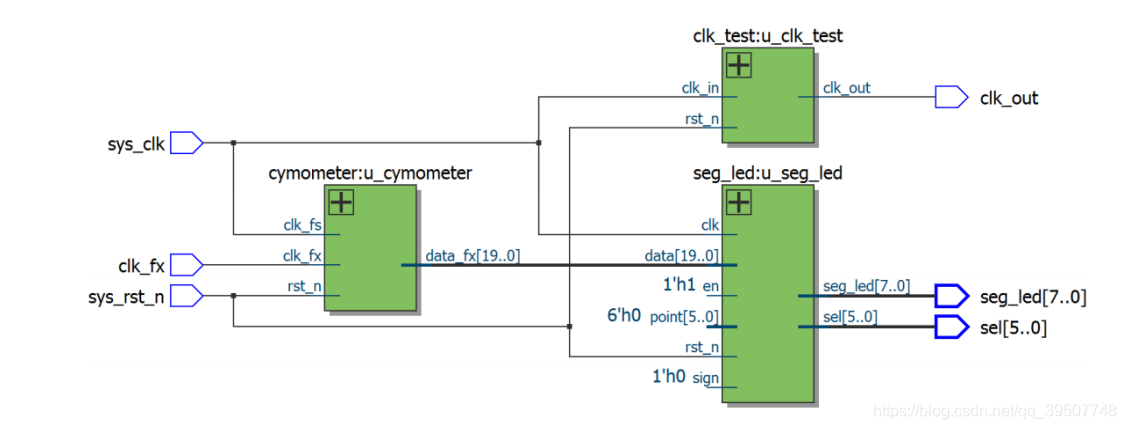
c
module top_cymometer(
//system clock
input sys_clk , // 时钟信号
input sys_rst_n, // 复位信号
//cymometer interface
input clk_fx , // 被测时钟
output clk_out , // 输出时钟
//user interface
output [5:0] sel , // 数码管位选
output [7:0] seg_led // 数码管段选
);
//parameter define
parameter CLK_FS = 26'd50000000; // 基准时钟频率值
//wire define
wire [19:0] data_fx; // 被测信号测量值
//*****************************************************
//** main code
//*****************************************************
//例化等精度频率计模块
cymometer #(.CLK_FS(CLK_FS) // 基准时钟频率值
) u_cymometer(
//system clock
.clk_fs (sys_clk ), // 基准时钟信号
.rst_n (sys_rst_n), // 复位信号
//cymometer interface
.clk_fx (clk_fx ), // 被测时钟信号
.data_fx (data_fx ) // 被测时钟频率输出
);
//例化测试时钟模块,产生测试时钟
clk_test #(.DIV_N(7'd100)// 分频系数
) u_clk_test(
//源时钟
.clk_in (sys_clk ), // 输入时钟
.rst_n (sys_rst_n), // 复位信号
//分频后的时钟
.clk_out (clk_out ) // 测试时钟
);
//例化数码管显示模块
seg_led u_seg_led(
//module clock
.clk (sys_clk ), // 数码管驱动模块的驱动时钟
.rst_n (sys_rst_n), // 复位信号
//seg_led interface
.sel (sel ), // 数码管位选
.seg_led (seg_led ), // 数码管段选
//user interface
.data(data_fx ), // 被测频率值
.point (6'd0 ), // 数码管显示的点控制
.en (1'b1 ), // 数码管驱动使能信号
.sign(1'b0 ) // 控制符号位显示
);
endmodule时钟产生模块(clk_test)
时钟产生模块通过分频产生被测时钟,这里是用偶数分频方法产生,修改代码第一行的 DIV_N 分频参数,可得到不同频率的时钟信号,时钟频率为 clk_in DIV_N \frac{\text{clk\_in}}{\text{DIV\_N}} DIV_Nclk_in。由于该模块在顶层例化时 clk_in 为系统时钟 50 MHz,分频参数为 100,产生的时钟频率为 50000000 100 = 500000 \frac{50000000}{100} = 500000 10050000000=500000 Hz。
c
module clk_test #(parameter DIV_N = 7'd100) //分频系数
(
//源时钟
input clk_in , // 输入时钟
input rst_n , // 复位信号
//分频后的时钟
output reg clk_out // 输出时钟
);
//reg define
reg [9:0] cnt; // 时钟分频计数
//*****************************************************
//** main code
//*****************************************************
//时钟分频
always @(posedge clk_in or negedge rst_n) begin
if(rst_n == 1'b0) begin
cnt <= 0;
clk_out <= 0;
end
else begin
if(cnt == DIV_N/2 - 1'b1) begin
cnt <= 10'd0;
clk_out <= ~clk_out;
end
else
cnt <= cnt + 1'b1;
end
end
endmodule等精度频率计模块(cymometer)
c
module cymometer
#(parameter CLK_FS = 26'd50_000_000) // 基准时钟频率值
( //system clock
input clk_fs , // 基准时钟信号
input rst_n , // 复位信号
//cymometer interface
input clk_fx , // 被测时钟信号
output reg [19:0] data_fx // 被测时钟频率输出
);
//parameter define
localparam MAX = 6'd32; // 定义fs_cnt、fx_cnt的最大位宽
localparam GATE_TIME = 16'd5_000;// 门控时间设置
//reg define
reg gate; // 门控信号
reg gate_fs ; // 同步到基准时钟的门控信号
reg gate_fs_r ; // 用于同步gate信号的寄存器
reg gate_fs_d0 ; // 用于采集基准时钟下gate下降沿
reg gate_fs_d1 ; //
reg gate_fx_d0 ; // 用于采集被测时钟下gate下降沿
reg gate_fx_d1 ; //
reg [ 15:0] gate_cnt ; // 门控计数
reg [MAX-1:0] fs_cnt ; // 门控时间内基准时钟的计数值
reg [MAX-1:0] fs_cnt_temp ; // fs_cnt 临时值
reg [MAX-1:0] fx_cnt ; // 门控时间内被测时钟的计数值
reg [MAX-1:0] fx_cnt_temp ; // fx_cnt 临时值
//wire define
wire neg_gate_fs; // 基准时钟下门控信号下降沿
wire neg_gate_fx; // 被测时钟下门控信号下降沿
//*****************************************************
//** main code
//*****************************************************
//边沿检测,捕获信号下降沿
assign neg_gate_fs = gate_fs_d1 & (~gate_fs_d0);
assign neg_gate_fx = gate_fx_d1 & (~gate_fx_d0);
//门控信号计数器,使用被测时钟计数
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n)
gate_cnt <= 16'd0;
else if(gate_cnt == GATE_TIME + 5'd20)
gate_cnt <= 16'd0;
else
gate_cnt <= gate_cnt + 1'b1;
end
//门控信号,拉高时间为GATE_TIME个实测时钟周期
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n)
gate <= 1'b0;
else if(gate_cnt < 4'd10)
gate <= 1'b0;
else if(gate_cnt < GATE_TIME + 4'd10)
gate <= 1'b1;
else if(gate_cnt <= GATE_TIME + 5'd20)
gate <= 1'b0;
else
gate <= 1'b0;
end
//将门控信号同步到基准时钟下
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
gate_fs_r <= 1'b0;
gate_fs <= 1'b0;
end
else begin
gate_fs_r <= gate;
gate_fs <= gate_fs_r;
end
end
//打拍采门控信号的下降沿(被测时钟下)
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n) begin
gate_fx_d0 <= 1'b0;
gate_fx_d1 <= 1'b0;
end
else begin
gate_fx_d0 <= gate;
gate_fx_d1 <= gate_fx_d0;
end
end
//打拍采门控信号的下降沿(基准时钟下)
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
gate_fs_d0 <= 1'b0;
gate_fs_d1 <= 1'b0;
end
else begin
gate_fs_d0 <= gate_fs;
gate_fs_d1 <= gate_fs_d0;
end
end
//门控时间内对被测时钟计数
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n) begin
fx_cnt_temp <= 32'd0;
fx_cnt <= 32'd0;
end
else if(gate)
fx_cnt_temp <= fx_cnt_temp + 1'b1;
else if(neg_gate_fx) begin
fx_cnt_temp <= 32'd0;
fx_cnt <= fx_cnt_temp;
end
end
//门控时间内对基准时钟计数
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
fs_cnt_temp <= 32'd0;
fs_cnt <= 32'd0;
end
else if(gate_fs)
fs_cnt_temp <= fs_cnt_temp + 1'b1;
else if(neg_gate_fs) begin
fs_cnt_temp <= 32'd0;
fs_cnt <= fs_cnt_temp;
end
end
//计算被测信号频率
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
data_fx <= 20'd0;
end
else if(gate_fs == 1'b0)
data_fx <= (CLK_FS / fs_cnt) * fx_cnt ;
end
endmodule 在前面的等精度频率计简介中,我们知道在等精度测量中需要一个闸门信号(门控信号),并且该闸门信号需要同步化到被测时钟域下。这里我们为了方便处理,用被测时钟控制闸门信号的产生,这样就避免了同步化处理,当然了,完全可以用基准时钟控制闸门信号的产生,不过这时产生的闸门信号我们需要同步化到被测时钟域下,这样做的目的是为了不让被测时钟计数产生 ±1 周期的误差。门控时间由参数 GATE_TIME 设置,此处设为 5000,需要说明的是该值越大测得的被测时钟频率值越精确,但测量时间也会相应的变慢一些。另外因为闸门信号是由被测时钟产生的,当测量频率较高的信号或者说信号频率大于 10KHz(此值跟门控时间有关)时是不会有什么问题的,但当测量低频信号像 Hz 级这种,如果门控时间设置的大的话,测量时间就会非常长,此时可修改门控时间的值,为被测时钟频率的 5~10 倍即可,对于几十 KHz 及以上的时钟信号,门控时间的大小对测量速度的影响较小,频率越高影响越小,但对测量精度影响较大,因而在测量频率较高的信号时,建议增大门控时间。
数码管显示模块(seg_led)
c
module seg_led(
//module clock
input clk ,// 时钟信号
input rst_n ,// 复位信号
//seg_led interface
output reg [5:0] sel ,// 动态显示被选中的数码管
output reg [7:0] seg_led,// 一个数码管中亮的灯,包含小数点
//user interface
input [19:0] data ,// 6个数码管要显示的数值
input [5:0] point ,// 小数点具体显示的位置,从高到低,高电平有效
input en ,// 数码管使能信号
input sign // 符号位(高电平显示"-"号)
);
//parameter define
localparam MAX_NUM = 13'd5000 ;// 1ms计数值
localparam CLK_DIVIDE = 4'd10 ;// 时钟分频
//reg define
reg [12:0] cnt0 ;// 1ms计数
reg flag ;// 1ms计满标志信号
reg [2:0] cnt ;// 切换显示数码管用
reg [3:0] num1 ;// 送给要显示的数码管,要亮的灯
reg point1 ;// 要显示的小数点
reg [23:0] num ;// 24位bcd码用寄存器
reg [ 3:0] clk_cnt ;// 时钟计数
reg dri_clk ;// 驱动数码管操作的驱动时钟
//wire define
wire [3:0] data0 ;// 十万位数
wire [3:0] data1 ;// 万位数
wire [3:0] data2 ;// 千位数
wire [3:0] data3 ;// 百位数
wire [3:0] data4 ;// 十位数
wire [3:0] data5 ;// 个位数
//*****************************************************
//** main code
//*****************************************************
assign data5 = data / 17'd100000; // 十万位数
assign data4 = data / 14'd10000 % 4'd10; // 万位数
assign data3 = data / 10'd1000 % 4'd10 ; // 千位数
assign data2 = data / 7'd100 % 4'd10 ; // 百位数
assign data1 = data / 4'd10 % 4'd10 ; // 十位数
assign data0 = data % 4'd10; // 个位数
//生成数码管的驱动时钟用于驱动数码管的操作
always @(posedge clk or negedge rst_n) begin
if(!rst_n) begin
dri_clk <= 1'b1;
clk_cnt <= 4'd0;
end
else if(clk_cnt == CLK_DIVIDE/2 - 1'd1) begin
clk_cnt <= 4'd0;
dri_clk <= ~dri_clk;
end
else
clk_cnt <= clk_cnt + 1'b1;
end
//将20位2进制数转换为8421bcd码
always @ (posedge dri_clk or negedge rst_n) begin
if (!rst_n)
num <= 24'b0;
else begin
if (data5 || point[5]) begin
num[23:20] <= data5;
num[19:16] <= data4;
num[15:12] <= data3;
num[11:8] <= data2;
num[ 7:4] <= data1;
num[ 3:0] <= data0;
end
else begin
if (data4 || point[4]) begin
num[19:0] <= {data4,data3,data2,data1,data0};
if(sign)
num[23:20] <= 4'd11;
else
num[23:20] <= 4'd10;
end
else begin
if (data3 || point[3]) begin
num[15: 0] <= {data3,data2,data1,data0};
num[23:20] <= 4'd10;
if(sign)
num[19:16] <= 4'd11;
else
num[19:16] <= 4'd10;
end
else begin
if (data2 || point[2]) begin
num[11: 0] <= {data2,data1,data0};
num[23:16] <= {2{4'd10}};
if(sign)
num[15:12] <= 4'd11;
else
num[15:12] <= 4'd10;
end
else begin
if (data1 || point[1]) begin
num[ 7: 0] <= {data1,data0};
num[23:12] <= {3{4'd10}};
if(sign)
num[11:8] <= 4'd11;
else
num[11:8] <= 4'd10;
end
else begin
num[3:0] <= data0;
if(sign)
num[23:4] <= {{4{4'd10}},4'd11};
else
num[23:4] <= {5{4'd10}};
end
end
end
end
end
end
end
end
end
//计数1ms
always @ (posedge dri_clk or negedge rst_n) begin
if (rst_n == 1'b0) begin
flag <= 1'b0;
cnt0 <= 13'b0;
end
else if (cnt0 < MAX_NUM - 1'b1) begin
flag <= 1'b0;
cnt0 <= cnt0 + 1'b1;
end
else begin
flag <= 1'b1;
cnt0 <= 13'b0;
end
end
//计数器,用来计数6个状态(因为有6个灯)
always @ (posedge dri_clk or negedge rst_n) begin
if (rst_n == 1'b0)
cnt <= 3'b0;
else if(flag) begin
if(cnt < 3'd5)
cnt <= cnt + 1'b1;
else
cnt <= 3'b0;
end
end
//6个数码管轮流显示,完成刷新( 从右到左)
always @ (posedge dri_clk or negedge rst_n) begin
if(!rst_n) begin
sel <= 6'b000000;
num1 <= 4'b0;
end
else begin
if(en) begin
case (cnt)
3'd0 :begin
sel <= 6'b111110;
num1 <= num[3:0] ;
point1 <= ~point[0] ;
end
3'd1 :begin
sel <= 6'b111101;
num1 <= num[7:4] ;
point1 <= ~point[1] ;
end
3'd2 :begin
sel <= 6'b111011;
num1 <= num[11:8];
point1 <= ~point[2] ;
end
3'd3 :begin
sel <= 6'b110111;
num1 <= num[15:12];
point1 <= ~point[3] ;
end
3'd4 :begin
sel <= 6'b101111;
num1 <= num[19:16];
point1 <= ~point[4];
end
3'd5 :begin
sel <= 6'b011111;
num1 <= num[23:20];
point1 <= ~point[5];
end
default :begin
sel <= 6'b000000;
num1 <= 4'b0;
point1 <= 1'b1;
end
endcase
end
else
sel <= 6'b111111;
end
end
//数码管显示数据
always @ (posedge dri_clk or negedge rst_n) begin
if (!rst_n)
seg_led <= 7'h40;
else begin
case (num1)
4'd0 : seg_led <= {point1,7'b1000000};
4'd1 : seg_led <= {point1,7'b1111001};
4'd2 : seg_led <= {point1,7'b0100100};
4'd3 : seg_led <= {point1,7'b0110000};
4'd4 : seg_led <= {point1,7'b0011001};
4'd5 : seg_led <= {point1,7'b0010010};
4'd6 : seg_led <= {point1,7'b0000010};
4'd7 : seg_led <= {point1,7'b1111000};
4'd8 : seg_led <= {point1,7'b0000000};
4'd9 : seg_led <= {point1,7'b0010000};
4'd10: seg_led <= 8'b11111111;
4'd11: seg_led <= 8'b10111111;
default : seg_led <= {point1,7'b1000000};
endcase
end
end
endmodule

由上式可以看出,测量频率的相对误差与被测信号频率的大小无关,仅与闸门时间和基准时钟频率有关,即实现了整个测试频段的等精度测量。闸门时间越长,基准时钟频率越高,测频的相对误差就越小。基准时钟频率可由稳定度好、精度高的高频率晶体振荡器产生,在保证测量精度不变的前提下,提高基准时钟频率,可使闸门时间缩短,即提高测试速度。
FPGA 频率测量的三种方法(直接测量法,间接测量法,等精度测量法)
孤独的单刀 已于 2023-06-05 02:30:24 修改
1、FPGA 频率测量?
频率测量在电子设计和测量领域中经常用到,因此对频率测量方法的研究在实际工程应用中具有重要意义。
通常的频率测量方法有三种:直接测量法,间接测量法,等精度测量法。
2、直接测量法
2.1、方法
直接测量法也叫频率测量法,即在固定时间 t t t 内对被测信号的脉冲数进行计数,然后求出单位时间内的脉冲数,即为被测信号的频率。
下图中的信号分别为:
sys_clk:系统的基准时钟gate:根据基准时钟生成的闸门信号,用于生成一个固定的时间(例如 1 s,方便计算)clk_fx:被测信号
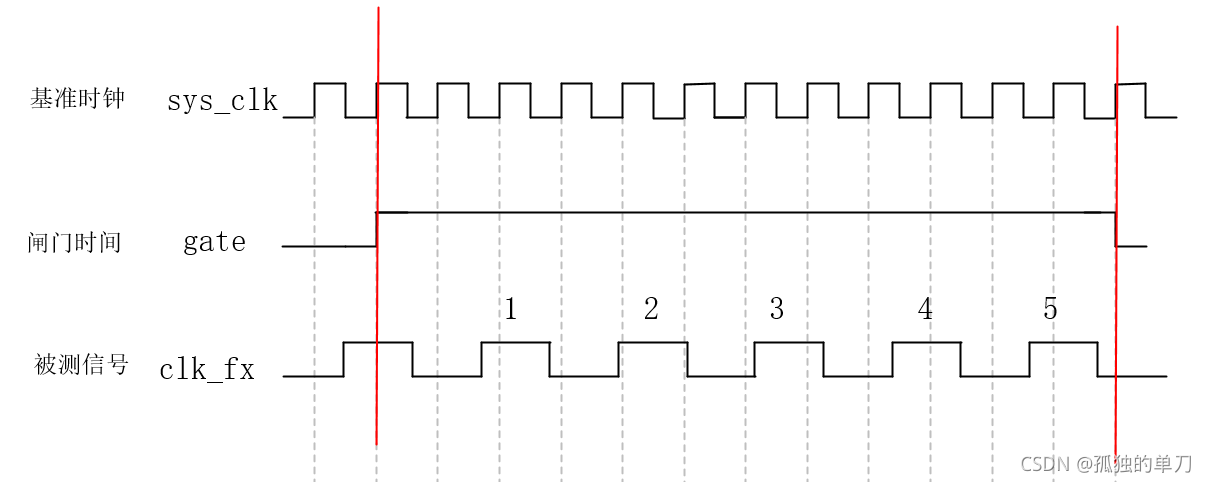
gate 是在基准时钟下生成的固定时间信号,它持续的时间 KaTeX parse error: Expected 'EOF', got '_' at position 16: T_g = \text{sys_̲clk} \times \te...(可设置);在 gate 持续为高的时间内,可使用被测信号 clk_fx 对其进行计数,计数个数为 cnt(图中为 5),则 cnt 个被测信号的周期即为 gate 时长。
此种方法的本质是:同样的时间内分别使用两种时钟计时,则有 T g = T f x = T sys_clk × 计数个数N = T clk_fx × cnt T_g = T_{fx} = T_{\text{sys\clk}} \times \text{计数个数N} = T{\text{clk\_fx}} \times \text{cnt} Tg=Tfx=Tsys_clk×计数个数N=Tclk_fx×cnt,公式变换后:
clk_fx = cnt × sys_clk 计数个数N ( 其中 clk_fx 为待测信号频率,sys_clk 为基准时钟频率 ) \text{clk\_fx} = \text{cnt} \times \frac{\text{sys\_clk}}{\text{计数个数N}} \quad (\text{其中 clk\_fx 为待测信号频率,sys\_clk 为基准时钟频率}) clk_fx=cnt×计数个数Nsys_clk(其中 clk_fx 为待测信号频率,sys_clk 为基准时钟频率)
2.2、误差分析
从图可以看出,在 gate 为高电平期间,被测信号实际上差不多有六个周期被囊括在内,但是因为被测信号是相对于系统的异步信号,相位不同,第一个周期无法被采样,所以实际采样为 5,这样造成的误差为一个被测信号周期。可以预见,这种测量方法带来的测量误差即为一个被测信号周期。
那么理论上测得的准确频率:
clk_fxe = cnt × sys_clk 计数个数N ( 理论上 cnt 无误差 ) \text{clk\_fxe} = \text{cnt} \times \frac{\text{sys\_clk}}{\text{计数个数N}} \quad (\text{理论上 cnt 无误差}) clk_fxe=cnt×计数个数Nsys_clk(理论上 cnt 无误差)
实际上测量的频率值:
clk_fx = ( cnt ± 1 ) × sys_clk 计数个数N ( cnt 会存在一个周期的测量误差 ) \text{clk\_fx} = (\text{cnt} \pm 1) \times \frac{\text{sys\_clk}}{\text{计数个数N}} \quad (\text{cnt 会存在一个周期的测量误差}) clk_fx=(cnt±1)×计数个数Nsys_clk(cnt 会存在一个周期的测量误差)
测量误差:
测量误差 = ∣ ( clk_fxe − clk_fx ) clk_fxe ∣ × 100 % = 1 cnt × 100 % \text{测量误差} = \left| \frac{(\text{clk\_fxe} - \text{clk\_fx})}{\text{clk\_fxe}} \right| \times 100\% = \frac{1}{\text{cnt}} \times 100\% 测量误差= clk_fxe(clk_fxe−clk_fx) ×100%=cnt1×100%
所以测得的 cnt 越大,那么测出来的误差值就越小,而 cnt 越大则代表被测信号的频率越高,所以可以推断该种测量方法适合测量高频信号;此外,选择的闸门时间越长则被测信号的个数越多,同样测量就越精确,但是增大闸门时间又会带来测量时间过长的问题,需要依据具体需求进行取舍。
2.3、Verilog 代码
Verilog 源码如下:
- 闸门时间设定为 0.5 s,非闸门时间也为 0.5 s,则每 1 s 更新一次测量数据
- 使用计数器生成闸门时间,闸门时间取反得到非闸门时间
- 在闸门时间对被测信号计数
- 在非闸门时间更新测量数据
- 使用 parameter 定义参数,方便调用修改
verilog
//直接测量法(高频)
module cymometer_direct(
input sys_clk , //基准时钟,设计为50M(可更改)
input sys_rst_n , //复位信号,低电平有效
input clk_fx , //待测信号
output reg [31:0] fre //测量结果
);
parameter TIME_SYS = 20 ; //系统时钟周期:20ns--频率=50MHz
parameter TIME_GATE = 500_000_000 ; //500ms闸门设置的时间,单位:ns
localparam N = TIME_GATE / TIME_SYS; //生成闸门需要计数的个数
reg gate ; //闸门
reg [31:0] cnt_gate ; //用于生成闸门的计数器
reg [31:0] cnt_fx ; //闸门时间内对被测信号计数
wire gate_n ; //闸门取反,用于在非闸门时输出测得的频率值
assign gate_n = ~gate ; //闸门取反,用于在非闸门时输出测得的频率值
//分频计数器,闸门时间设定为1ms,则每2ms测量一次
always @(posedge sys_clk or negedge sys_rst_n)begin
if(!sys_rst_n)begin
cnt_gate <=0;
gate <=0;
end
else begin
if(cnt_gate == N-1)begin
cnt_gate <= 0;
gate <= ~gate;
end
else
cnt_gate<=cnt_gate+1;
end
end
//闸门时间内对被测信号计数
always @(posedge clk_fx or negedge sys_rst_n)begin
if(!sys_rst_n)
cnt_fx <= 0;
else if(gate)
cnt_fx <= cnt_fx + 1;
else
cnt_fx <= 0;
end
//在非闸门时输出测得的频率值
always @(posedge gate_n or negedge sys_rst_n)begin
if(!sys_rst_n)
fre <= 0;
else
//TIME_GATE/cnt_fx=规定时间/被测信号个数=被测信号周期,取倒数即为频率
fre <= 1000_000_000/TIME_GATE * cnt_fx;
end
endmodule2.4、仿真分析
Testbench:
设计被测信号周期为 489 × 2 = 978 489 \times 2 = 978 489×2=978 ns,则其理论频率为 1 978 ns = 1022494.88 \frac{1}{978 \text{ns}} = 1022494.88 978ns1=1022494.88 Hz;
verilog
`timescale 1ns/1ns //时间单位/精度
//------------<模块及端口声明>----------------------------------------
module tb_cymometer_direct();
reg sys_clk;
reg sys_rst_n;
reg clk_fx;
wire [31:0] fre;
// defparam cymometer_direct_inst.TIME_GATE = 500_000; //地址位宽
//------------<例化被测试模块>----------------------------------------
cymometer_direct cymometer_direct_inst(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx ),
.fre (fre )
);
//------------<设置初始测试条件>----------------------------------------
initial begin
sys_clk = 1'b0; //初始时钟为0
sys_rst_n <= 1'b0; //初始复位
clk_fx <= 1'b0;
#5 //5个时钟周期后
sys_rst_n <= 1'b1; //拉高复位,系统进入工作状态
// #2500_000
// forever #2560 clk_fx = ~clk_fx;
end
//------------<设置时钟>----------------------------------------------
always #10 sys_clk = ~sys_clk; //系统时钟周期20ns
always #489 clk_fx = ~clk_fx; //被测信号周期489*2ns = 978ns
endmodule仿真如下图:
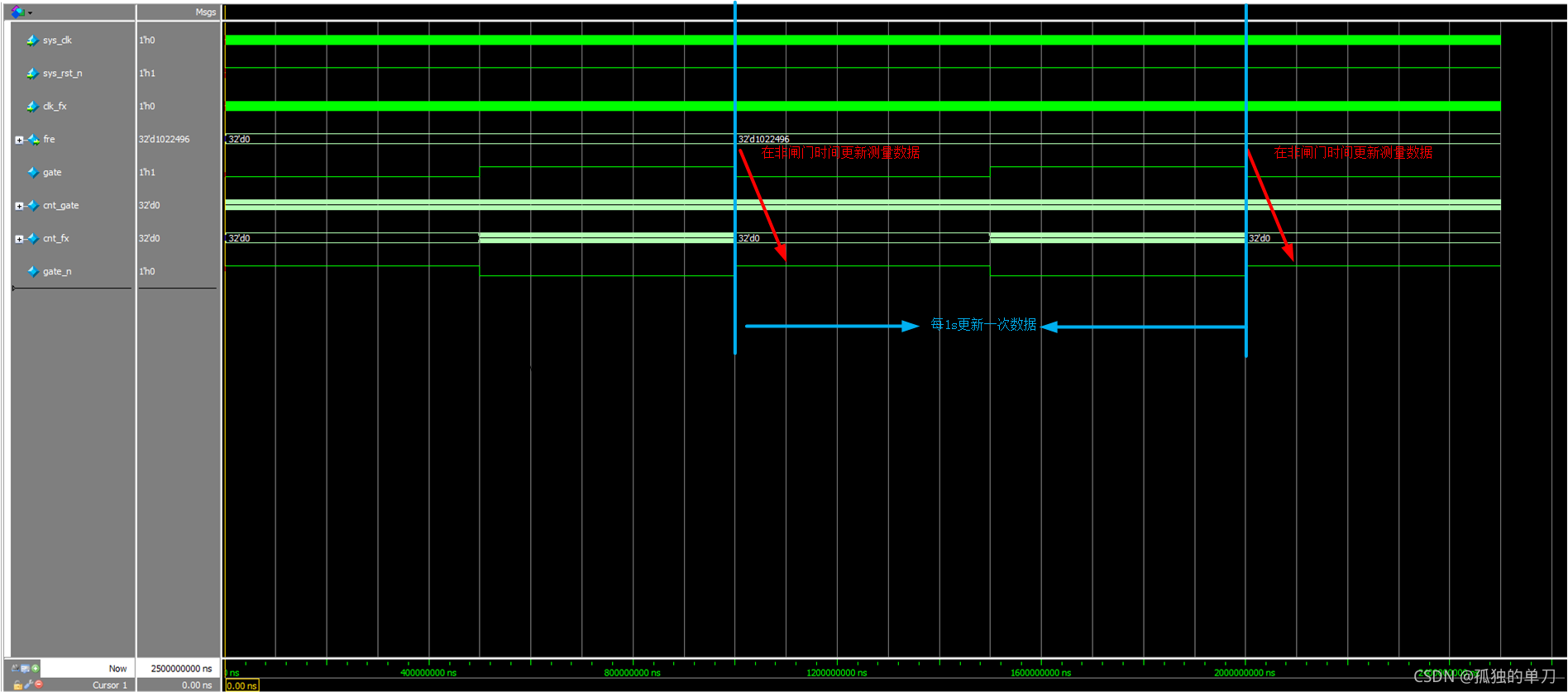
上图在闸门时间内测得的被测信号个数 cnt_fx 为 511248,测得被测信号频率为 1022496 Hz;理论频率 = 1 978 ns = 1022494.88 = \frac{1}{978 \text{ns}} = 1022494.88 =978ns1=1022494.88 Hz(MHz 级别)。
可以看出这个测量结果还是比较准确的。因为闸门时间够长,且被测信号自身频率就比较高(约 1 MHz)。
接下来更改一下 Testbench,比较一下闸门时间对被测信号的影响以及被测信号自身频率高低对测量的影响:
- 第 1 个模块:被测信号频率为 1022494.88 Hz(MHz 级别),闸门时间 0.5 s
- 第 2 个模块:被测信号频率为 1022494.88 Hz(MHz 级别),闸门时间 0.5 ms
- 第 3 个模块:被测信号频率为 76103.5 Hz(KHz 级别),闸门时间 0.5 s
- 第 4 个模块:被测信号频率为 21.217 Hz(Hz 级别),闸门时间 0.5 s
verilog
//多变量对比测试
`timescale 1ns/1ns //时间单位/精度
//------------<模块及端口声明>----------------------------------------
module tb_cymometer_direct();
reg sys_clk;
reg sys_rst_n;
reg clk_fx1;
reg clk_fx2;
reg clk_fx3;
reg clk_fx4;
wire [31:0] fre1;
wire [31:0] fre2;
wire [31:0] fre3;
wire [31:0] fre4;
defparam cymometer_direct_inst2.TIME_GATE = 500_000; //重设闸门时间1ms
//------------<例化被测试模块>----------------------------------------
cymometer_direct cymometer_direct_inst1(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx1 ),
.fre (fre1 )
);
cymometer_direct cymometer_direct_inst2(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx2 ),
.fre (fre2 )
);
cymometer_direct cymometer_direct_inst3(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx3 ),
.fre (fre3 )
);
cymometer_direct cymometer_direct_inst4(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx4 ),
.fre (fre4 )
);
//------------<例化被测试模块>----------------------------------------
//------------<设置初始测试条件>----------------------------------------
initial begin
sys_clk = 1'b0; //初始时钟为0
sys_rst_n <= 1'b0; //初始复位
clk_fx1 <= 1'b0;
clk_fx2 <= 1'b0;
clk_fx3 <= 1'b0;
clk_fx4 <= 1'b0;
#5 //5个时钟周期后
sys_rst_n <= 1'b1; //拉高复位,系统进入工作状态
end
//------------<设置时钟>----------------------------------------------
always #10 sys_clk = ~sys_clk; //系统时钟周期20ns
always #489 clk_fx1 = ~clk_fx1; //被测信号周期489*2ns,理论频率1022494.88Hz(MHz级别)
always #489 clk_fx2 = ~clk_fx2; //被测信号周期489*2ns,理论频率1022494.88Hz(MHz级别)
always #6570 clk_fx3 = ~clk_fx3; //被测信号周期6570*2ns,理论频率76103.5Hz(KHz级别)
always #23565678 clk_fx4 = ~clk_fx4; //被测信号周期23565678*2ns,理论频率21.217Hz(Hz级别)
endmodule测量结果如下:
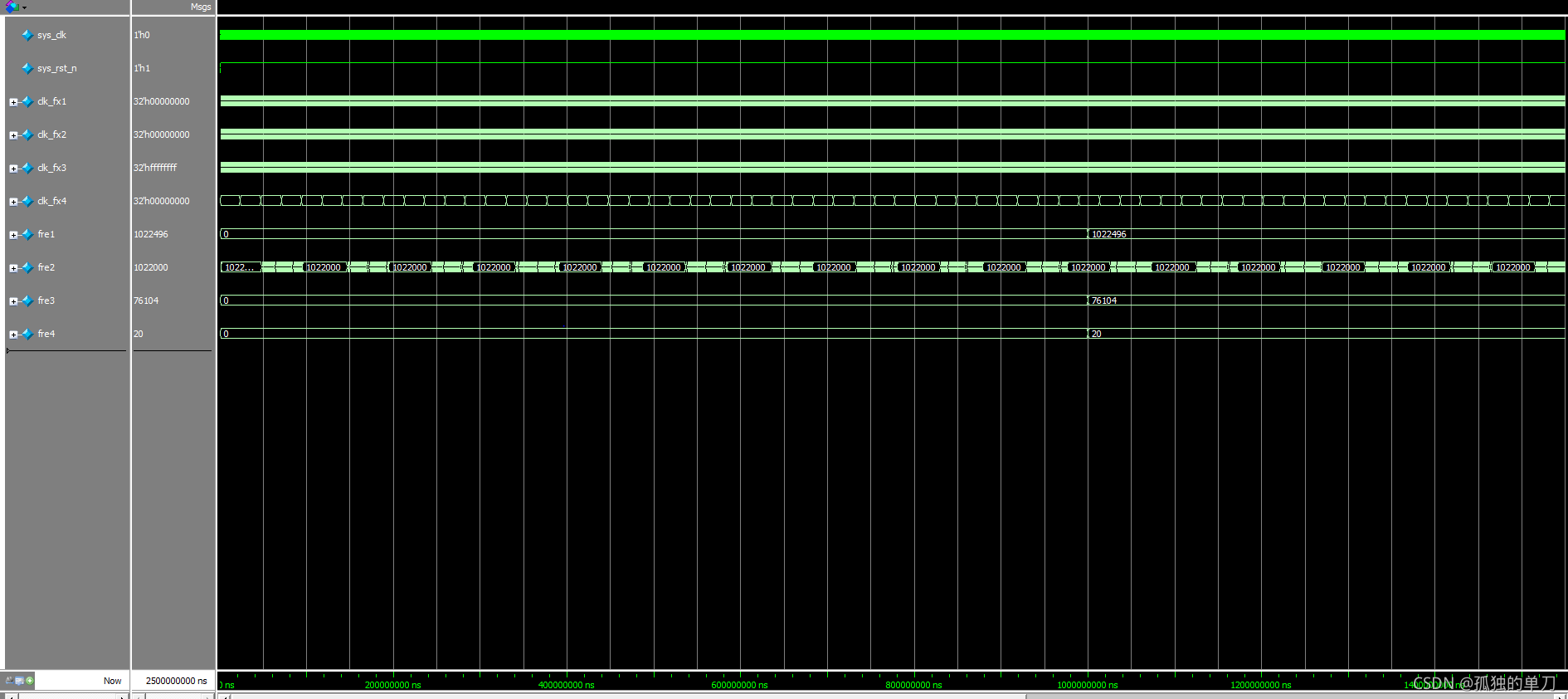
将测量结果整理成下表:
| 模块 | 闸门时间 | 理论频率 (Hz) | 实际测量频率 (Hz) | 测量误差 |
|---|---|---|---|---|
| 模块1 | 0.5 s | 1022494.88 | 1022496 | 0.0001095% |
| 模块2 | 0.5 ms | 1022494.88 | 1022000 | 0.0004840% |
| 模块3 | 0.5 s | 76103.5 | 76104 | 0.0006570% |
| 模块4 | 0.5 s | 21.217 | 20 | 0.05736% |
从上表的测试结果可以对直接测量法做出如下总结:
- 闸门时间越长,测量结果越精准,但是也会导致单次测量时间过长。
- 直接测量法适合测量高频信号,测量误差与闸门时间及被测信号频率相关。
3、间接测量法
3.1、方法
间接测量法也叫周期测量法,即在一个被测信号的周期内,测量基准时钟的个数,得到被测信号的周期,再将其转化为频率。
下图中的信号分别为:
sys_clk:系统的基准时钟clk_fx:被测信号
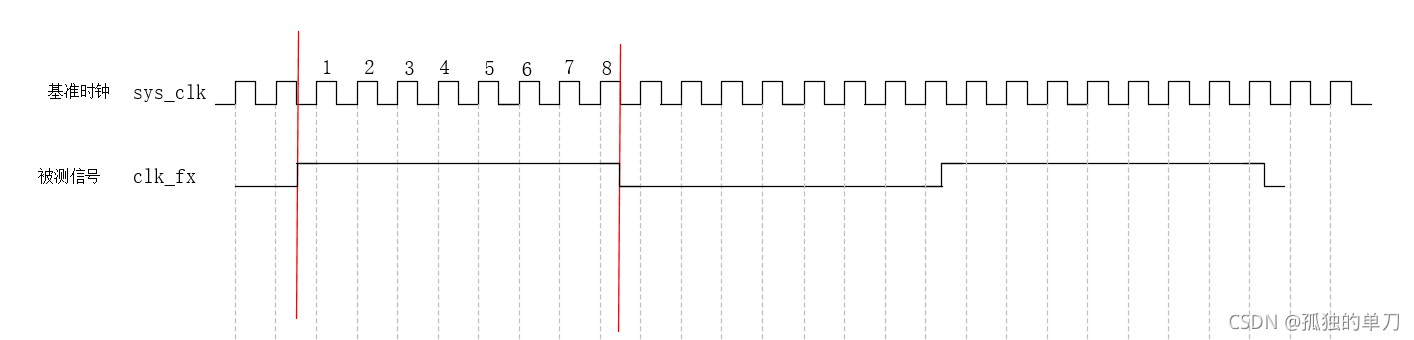
在被测信号 clk_fx 为高电平的时间内,使用基准时钟进行计数,计数个数为 cnt(图中为 8),则 cnt × 基准时钟周期 = 1 2 × 被测信号的周期 \text{cnt} \times \text{基准时钟周期} = \frac{1}{2} \times \text{被测信号的周期} cnt×基准时钟周期=21×被测信号的周期。
所以 KaTeX parse error: Expected 'EOF', got '' at position 29: ...nt}}{\text{FERQ_̲SYS} (\text{基准时...,化简后 KaTeX parse error: Expected 'EOF', got '' at position 10: \text{clk_̲fx} = \frac{\te...。
此种方法适用于测量低频信号,但同时也会带来测量速度过慢的问题,误差来自一个系统基准时钟。
3.2、误差分析
从图可以看出,在被测信号高电平期间,被测信号实际上差不多有 8.5 个周期被囊括在内,但是因为被测信号是相对于系统的异步信号,相位不同,所以实际采样为 8,这样造成的误差为 1 个基准信号周期。可以预见,这种测量方法带来的测量误差即为一个基准信号周期。
那么理论上测得的准确频率:
clk_fx = FERQ_SYS ( cnt × 2 ) ( 理论上 cnt 无误差 ) \text{clk\_fx} = \frac{\text{FERQ\_SYS}}{(\text{cnt} \times 2)} \quad (\text{理论上 cnt 无误差}) clk_fx=(cnt×2)FERQ_SYS(理论上 cnt 无误差)
实际上测量的频率值:
clk_fx = FERQ_SYS ( ( cnt ± 1 ) × 2 ) ( cnt 会存在一个周期的测量误差 ) \text{clk\_fx} = \frac{\text{FERQ\_SYS}}{((\text{cnt} \pm 1) \times 2)} \quad (\text{cnt 会存在一个周期的测量误差}) clk_fx=((cnt±1)×2)FERQ_SYS(cnt 会存在一个周期的测量误差)
测量误差:
测量误差 = ∣ ( clk_fxe − clk_fx ) clk_fxe ∣ × 100 % = 1 cnt × 100 % \text{测量误差} = \left| \frac{(\text{clk\_fxe} - \text{clk\_fx})}{\text{clk\_fxe}} \right| \times 100\% = \frac{1}{\text{cnt}} \times 100\% 测量误差= clk_fxe(clk_fxe−clk_fx) ×100%=cnt1×100%
所以测得的 cnt 越大,那么测出来的误差值就越小,而 cnt 越大则代表被测信号的频率越低(周期越高),所以可以推断该种测量方法适合测量低频信号。
3.3、Verilog 代码
Verilog 源码如下:
- 在被测信号计数高电平期间使用基准时钟计数
- 在被测信号计数低电平期间更新测量数据
- 使用 parameter 定义参数,方便调用修改
verilog
//间接测量法(低频)
module cymometer_indirect(
input sys_clk , //基准时钟,设计为50M(可更改)
input sys_rst_n , //复位信号,低电平有效
//待测信号
input clk_fx , //测量结果
output reg [31:0] fre
);
parameter TIME_SYS = 20 ; //系统时钟周期:20ns--频率=50MHz
reg [31:0] cnt_fx; //对被测信号高电平进行计数的计数器
//在测信号高电平期间进行计数
always @(posedge sys_clk or negedge sys_rst_n)begin
if(!sys_rst_n)
cnt_fx <= 0;
else if(clk_fx)
cnt_fx <= cnt_fx+1;
else
cnt_fx <= 0;
end
//在测信号低电平期输出测量数据
always @(negedge clk_fx or negedge sys_rst_n )begin
if(!sys_rst_n)
fre<=0;
else
fre<=1000_000_000/(TIME_SYS*cnt_fx*2);
end
endmodule3.4、仿真分析
Testbench 依然采用在直接测量法测试用的 3 个频率设置:
- 模块 1:被测信号周期 (23565678 \times 2) ns,理论频率 21.217 Hz(Hz 级别)
- 模块 2:被测信号周期 (6570 \times 2) ns,理论频率 76103.5 Hz(KHz 级别)
- 模块 3:被测信号周期 (489 \times 2) ns,理论频率 1022494.88 Hz(MHz 级别)
verilog
`timescale 1ns/1ns //时间单位/精度
//------------<模块及端口声明>----------------------------------------
module tb_cymometer_indirect();
reg sys_clk;
reg sys_rst_n;
reg clk_fx1;
reg clk_fx2;
reg clk_fx3;
wire [31:0] fre1;
wire [31:0] fre2;
wire [31:0] fre3;
//------------<例化被测试模块>----------------------------------------
cymometer_indirect cymometer_indirect_inst1(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx1 ),
.fre (fre1 )
);
cymometer_indirect cymometer_indirect_inst2(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx2 ),
.fre (fre2 )
);
cymometer_indirect cymometer_indirect_inst3(
.sys_clk (sys_clk ),
.sys_rst_n (sys_rst_n ),
.clk_fx (clk_fx3 ),
.fre (fre3 )
);
//------------<设置初始测试条件>----------------------------------------
initial begin
sys_clk = 1'b0; //初始时钟为0
sys_rst_n <= 1'b0; //初始复位
clk_fx1 <= 1'b0;
clk_fx2 <= 1'b0;
clk_fx3 <= 1'b0;
#5 //5个时钟周期后
sys_rst_n <= 1'b1; //拉高复位,系统进入工作状态
end
//------------<设置时钟>----------------------------------------------
always #10 sys_clk = ~sys_clk; //系统时钟周期20ns
always #23565678 clk_fx1 = ~clk_fx1; //被测信号周期23565678*2ns,理论频率21.217Hz(Hz级别)
always #6570 clk_fx2 = ~clk_fx2; //被测信号周期6570*2ns,理论频率76103.5Hz(KHz级别)
always #489 clk_fx3 = ~clk_fx3; //被测信号周期489*2ns,理论频率1022494.88Hz(MHz级别)
endmodule仿真如下图:
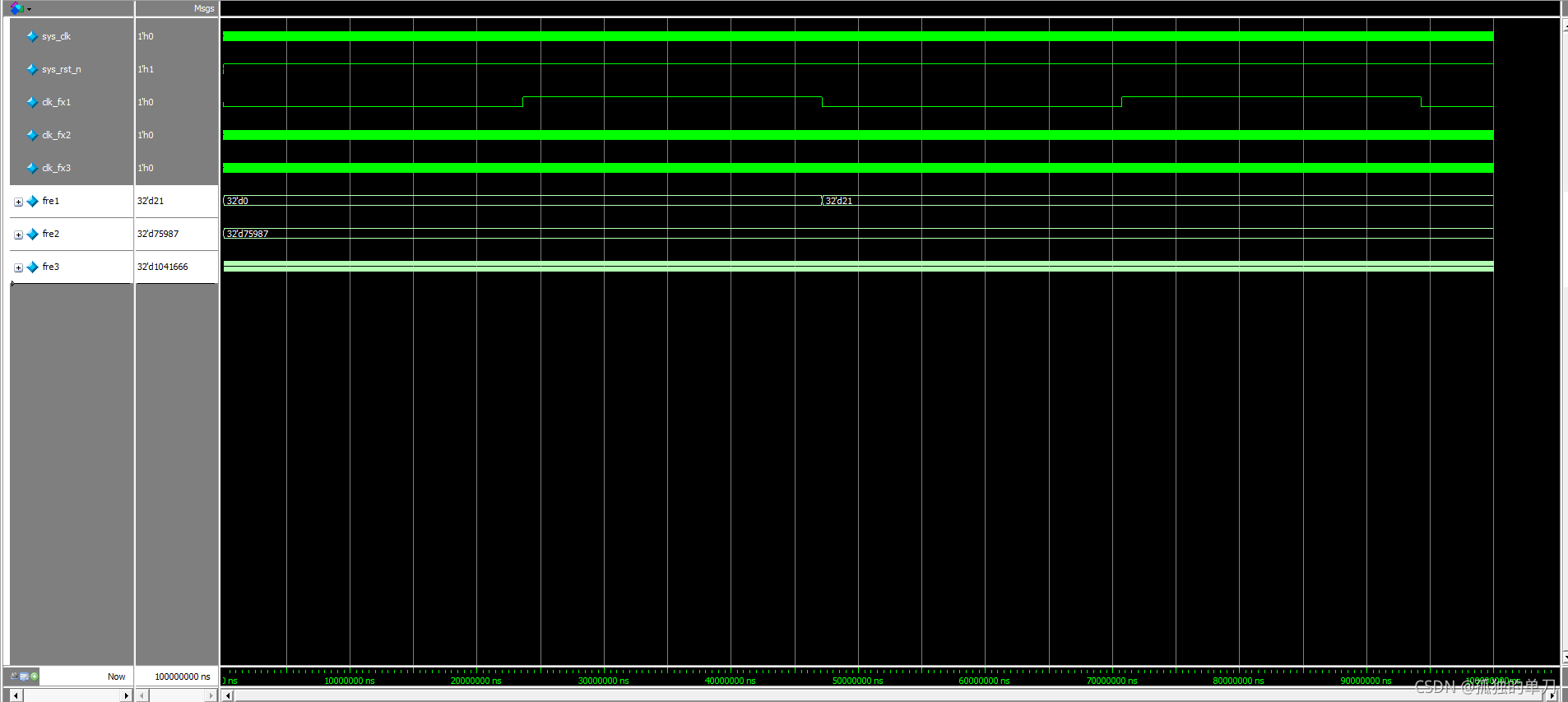
将测量结果整理成下表:
| 模块 | 理论频率 (Hz) | 实际测量频率 (Hz) | 测量误差 |
|---|---|---|---|
| 模块1 | 21.217297 | 21 | 0.0102% |
| 模块2 | 76103.5 | 75987 | 0.0015% |
| 模块3 | 1022494.88 | 1041666 | 0.0187% |
从上表的测试结果可以对间接测量法做出如下总结:间接测量法适合测量低频信号,测量误差与被测信号频率相关。
需要注意的是,输出信号不能处理浮点数,推荐的解决办法是将其放大整数倍(100 倍),以便实现小数点的频率测量(不然小数点被截断会带来额外的误差)。将测量结果乘以 1000,一定程度上消除小数截断带来的误差,模块 1 的测试结果为 21.217 Hz,测量误差为 0.0019998%,大大低于另外两个高频信号。(这里不给出具体的测试过程了,可以自己尝试下)。
4、等精度测量法
4.1、概念
上述两种方法都会产生 ±1 个被测时钟周期的误差,在实际应用中有一定的局限性。而且根据两种方式的测量原理,很容易发现频率测量法适合于测量高频时钟信号,而周期测量法适合于低频时钟信号的测量,但二者都不能兼顾高低频率同样精度的测量要求。
等精度测量法与前两种方式不同,其最大的特点是,测量的实际门控时间不是一个固定值,它与被测时钟信号相关,是被测时钟信号周期的整数倍。在实际门控信号下,同时对标准时钟和被测时钟信号的时钟周期进行计数,再通过公式计算得到被测信号的时钟频率。由于实际门控信号是被测时钟周期的整数倍,就消除了被测信号产生的 ±1 时钟周期的误差,但是会产生对标准时钟信号 ±1 时钟周期的误差,而标准时钟通常又是频率极高,所以误差较之前两种方法就大大降低。
此种测量方法相对误差与被测信号频率的大小无关,仅与闸门时间和基准时钟频率有关,即实现了整个测试频段的等精度测量。闸门时间越长,基准时钟频率越高,测频的相对误差越小。需要注意的是,原则上门控时间越长,则精度越高,但测量低频信号(Hz 级别)时,建议将门控时间设置为被测信号的十几倍即可,否则测量时间将会过长。
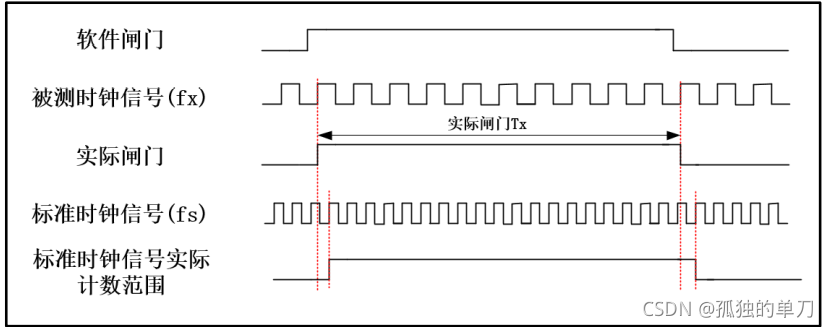
了解了等精度测量原理之后,我们来说明一下被测时钟信号的计算方法:
- 首先通过被测信号生成实际闸门。
- 分别对实际闸门下被测时钟信号和标准时钟信号的时钟周期进行计数。
- 实际闸门下被测时钟信号周期数为 X X X,设被测信号时钟周期为 T f x T_{fx} Tfx,它的时钟频率 f x = 1 T f x f_x = \frac{1}{T_{fx}} fx=Tfx1,由此可得等式: X × T f x = X f x = T x X \times T_{fx} = \frac{X}{f_x} = T_x X×Tfx=fxX=Tx(实际闸门)----这里无误差。
- 实际闸门下标准时钟信号周期数为 Y Y Y(误差为 1),设基准时钟周期为 T f s T_{fs} Tfs,它的时钟频率 f s = 1 T f s f_s = \frac{1}{T_{fs}} fs=Tfs1,由此可得等式: Y × T f s = Y f s = T x Y \times T_{fs} = \frac{Y}{f_s} = T_x Y×Tfs=fsY=Tx(实际闸门)----这里最大误差为 1 个基准时钟周期。
- 将两等式结合得到只包含各自时钟周期计数和时钟频率的等式: X f x = Y f s = T x \frac{X}{f_x} = \frac{Y}{f_s} = T_x fxX=fsY=Tx(实际闸门),等式变换,得到被测时钟信号时钟频率计算公式: f x = X × f s Y f_x = \frac{X \times f_s}{Y} fx=YX×fs。
- 将已知量标准时钟信号时钟频率 f s f_s fs 和测量量 X X X、 Y Y Y 带入计算公式,得到被测时钟信号时钟频率 f x f_x fx。
4.2、误差分析
根据前文及上图,不难发现,误差来源于使用基准时钟在闸门时间测量时会存在一个基准时钟周期的误差。
那么理论上测得的准确频率:
clk_fxe = X × f s Y ( 理论上 Y 无误差 ) \text{clk\_fxe} = \frac{X \times f_s}{Y} \quad (\text{理论上 Y 无误差}) clk_fxe=YX×fs(理论上 Y 无误差)
实际上测量的频率值:
clk_fx = X × f s Y ( Y 会存在 1 个周期的测量误差 ) \text{clk\_fx} = \frac{X \times f_s}{Y} \quad (Y \text{ 会存在 1 个周期的测量误差}) clk_fx=YX×fs(Y 会存在 1 个周期的测量误差)
测量误差:
测量误差 = ∣ ( clk_fxe − clk_fx ) clk_fxe ∣ × 100 % = 1 Y × 100 % \text{测量误差} = \left| \frac{(\text{clk\_fxe} - \text{clk\_fx})}{\text{clk\_fxe}} \right| \times 100\% = \frac{1}{Y} \times 100\% 测量误差= clk_fxe(clk_fxe−clk_fx) ×100%=Y1×100%
所以测得的 Y Y Y 越大,那么测出来的误差值就越小。当闸门时间越大, Y Y Y 越大;基准时钟频率越高, Y Y Y 越大。所以通过提高基准时钟频率或者增加闸门时间(但是会使测量过长,需要取舍),可以有效提高测量精度。
4.3、Verilog 代码
Verilog 源码如下:
verilog
//等精度测量法(低频)
module cymometer_equal (
input clk_fs ,
input rst_n ,
input clk_fx ,
output reg [63:0] fre
);
parameter CLK_FS = 26'd50_000_000;
parameter GATE_TIME = 16'd100; //门控时间,越大误差越小,但测量时间也会变长
//reg define
reg gate_fx ; //门控信号,被测信号域下
reg gate_fs ; //同步到基准时钟的门控信号
reg gate_fs_r ; //用于同步gate信号的寄存器
reg gate_fs_d0 ; //用于采集基准时钟下gate下降沿
reg gate_fs_d1 ; //用于采集基准时钟下gate下降沿
reg gate_fx_d0 ; //用于采集被测时钟下gate下降沿
reg gate_fx_d1 ; //用于采集被测时钟下gate下降沿
reg [15:0] gate_cnt ; //门控计数
reg [31:0] fs_cnt ; //门控时间内基准时钟的计数值
reg [31:0] fs_cnt_temp ; //fs_cnt 临时值
reg [31:0] fx_cnt ; //门控时间内被测时钟的计数值
reg [31:0] fx_cnt_temp ; //fx_cnt 临时值
//wire define
wire neg_gate_fs; //基准时钟下门控信号下降沿
wire neg_gate_fx; //被测时钟下门控信号下降沿
//捕捉信号下降沿
assign neg_gate_fs = gate_fs_d1 & (~gate_fs_d0);
assign neg_gate_fx = gate_fx_d1 & (~gate_fx_d0);
//检测gate_fx下降沿
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n) begin
gate_fx_d0 <= 1'b0;
gate_fx_d1 <= 1'b0;
end
else begin
gate_fx_d0 <= gate_fx;
gate_fx_d1 <= gate_fx_d0;
end
end
//检测gate_fs下降沿
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
gate_fs_d0 <= 1'b0;
gate_fs_d1 <= 1'b0;
end
else begin
gate_fs_d0 <= gate_fs;
gate_fs_d1 <= gate_fs_d0;
end
end
//被测时钟闸门计数器
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n)
gate_cnt <= 16'd0;
else if(gate_cnt == GATE_TIME*2)
gate_cnt <= 16'd0;
else
gate_cnt <= gate_cnt + 1'b1;
end
//被测时钟闸门生成
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n)
gate_fx <= 1'b0;
else if(gate_cnt == GATE_TIME)
gate_fx <= 1'b1;
else if(gate_cnt == GATE_TIME*2)
gate_fx <= 1'b0;
else
gate_fx <= gate_fx;
end
//把闸门从被测时钟域同步到基准时钟域
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
gate_fs_r <= 1'b0;
gate_fs <= 1'b0;
end
else begin
gate_fs_r <= gate_fx;
gate_fs <= gate_fs_r;
end
end
//在被测时钟域对被测信号计数
always @(posedge clk_fx or negedge rst_n) begin
if(!rst_n) begin
fx_cnt_temp <= 0;
fx_cnt <= 0;
end
else if(gate_fx)
fx_cnt_temp <= fx_cnt_temp + 1'b1;
else if(neg_gate_fx) begin
fx_cnt_temp <= 0;
fx_cnt <= fx_cnt_temp;
end
end
//在基准时钟域对基准时钟计数
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
fs_cnt_temp <= 0;
fs_cnt <= 0;
end
else if(gate_fs)
fs_cnt_temp <= fs_cnt_temp + 1'b1;
else if(neg_gate_fs) begin
fs_cnt_temp <= 0;
fs_cnt <= fs_cnt_temp;
end
end
//在基准时钟域输出结果
always @(posedge clk_fs or negedge rst_n) begin
if(!rst_n) begin
fre <= 0;
end
else if(gate_fs == 1'b0)
fre <= (CLK_FS * fx_cnt ) / fs_cnt;
end
endmodule 4.4、仿真分析
Testbench:
设计被测信号周期为 (489 \times 2 = 978) ns,则其理论频率为 1 978 ns = 1022494.88 \frac{1}{978 \text{ns}} = 1022494.88 978ns1=1022494.88 Hz。
verilog
`timescale 1 ns/ 1 ns
//------------<模块及端口声明>----------------------------------------
module tb_cymometer_equal();
reg clk_fs;
reg clk_fx;
reg rst_n;
wire [63:0] fre;
//------------<例化被测试模块>----------------------------------------
cymometer_equal cymometer_equal_inst (
.clk_fs (clk_fs ) ,
.clk_fx (clk_fx ) ,
.fre (fre ) ,
.rst_n (rst_n )
);
//------------<设置初始测试条件>----------------------------------------
initial begin
clk_fs = 1'b0;
clk_fx <= 1'b0;
rst_n <= 1'b0;
#116
rst_n <= 1'b1;
end
//------------<设置时钟>----------------------------------------------
always #10 clk_fs <= ~clk_fs;
always #489 clk_fx <= ~clk_fx;
endmodule仿真结果如下所示:
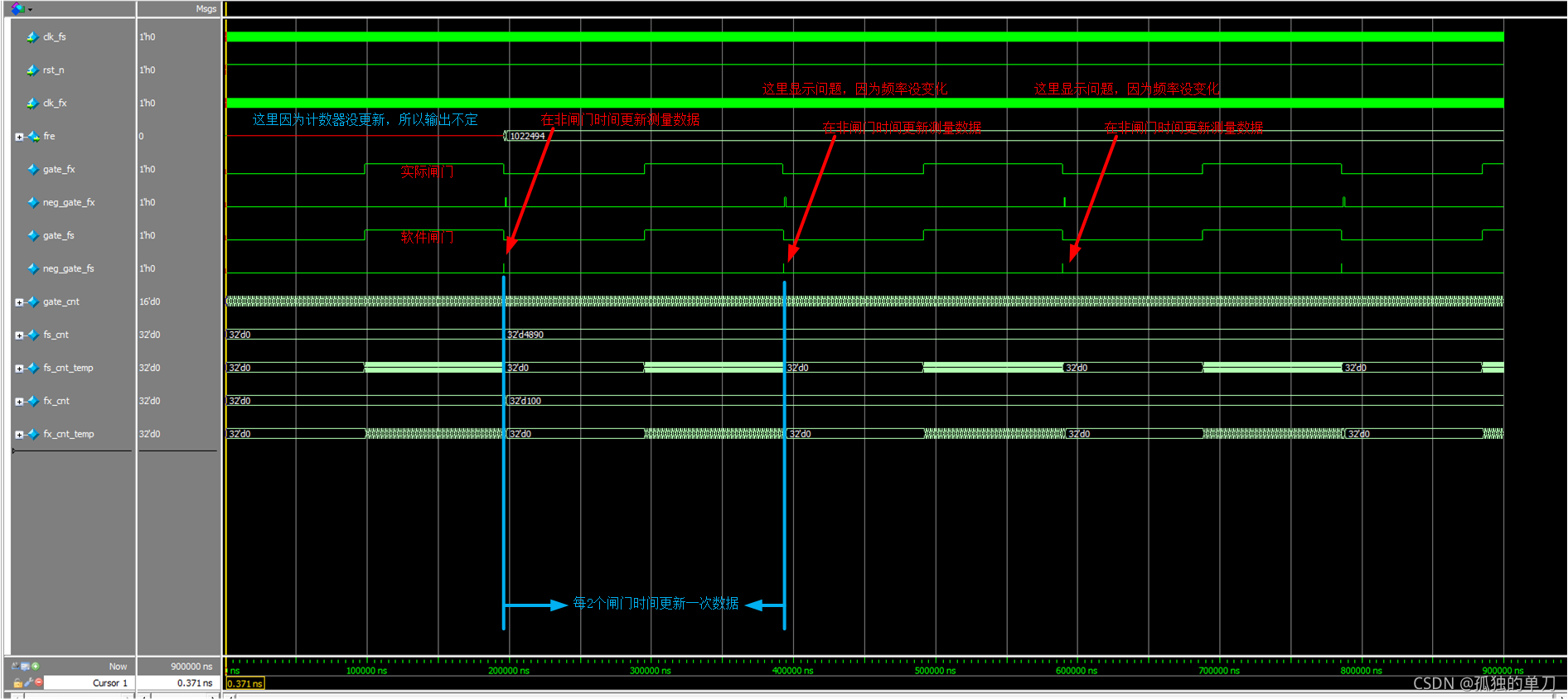
上图的测量结果为 1022494 Hz,理论频率 = 1 978 ns = 1022494.88 = \frac{1}{978 \text{ns}} = 1022494.88 =978ns1=1022494.88 Hz,可以看到这个结果相当精确。
接下来更改一下 Testbench,比较一下闸门时间对被测信号的影响以及被测信号自身频率高低对测量的影响(为避免仿真时间过长,闸门时间均设为 10 个被测信号周期,因为基准时钟频率较高,所以闸门时间少点不会有什么影响):
- 第 1 个模块:被测信号频率为 1022494.88 Hz(MHz 级别)
- 第 2 个模块:被测信号频率为 76103.5 Hz(KHz 级别)
- 第 3 个模块:被测信号频率为 21.217 Hz(Hz 级别)
仿真结果如下:
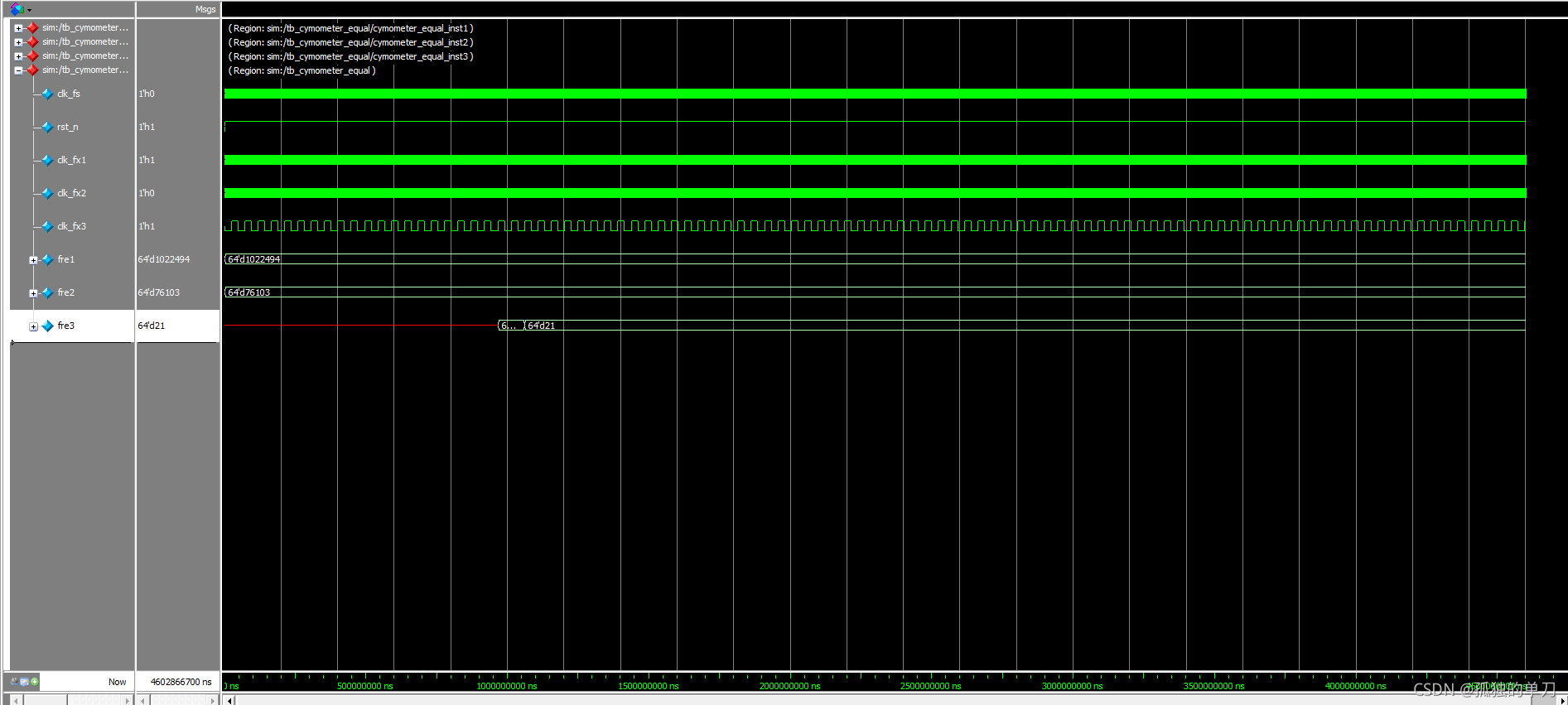
将测量结果整理成下表:
| 模块 | 理论频率 (Hz) | 实际测量频率 (Hz) | 测量误差 |
|---|---|---|---|
| 模块1 | 1022494.88 | 1022494 | 0.000086% |
| 模块2 | 76103.5 | 76103 | 0.000657% |
| 模块3 | 21.217297 | 21 | 0.0102% |
从上表的测试结果发现等精度测量法同时适用于高低频域,测量结果误差只和基准时钟频率有关。
这里需要注意的是,因为测量结果都是整数(FPGA 自动截断小数),如果被测频率较低,那么因为小数被截断,会使得误差增大。一个比较方便的解决办法是把计算公式都放大一定的倍数,从而使得"小数点前移"。将测量结果乘以 1000,一定程度上消除小数截断带来的误差,模块 3 的测试结果为 21.217 Hz,测量误差为 0.0019998%,基本和另外两个信号处于同一数量级。(这里不给出具体的测试过程了,可以自己尝试下)。
5、总结
- 直接测量法:适合测量高频信号;频率越高、测量时间越长,测量结果越精准。
- 间接测量法:适合测量低频信号,但测量精度取决于自身频率。
- 等精度测量法:相对误差与被测信号频率的大小无关,仅与闸门时间和基准时钟频率有关,即实现了整个测试频段的等精度测量。闸门时间越长,基准时钟频率越高,测频的相对误差就越小。
如果需要完整的工程文件 请点这里:工程文件下载
via:
-
等精度测频的原理和基于 FPGA 的实现_等精度测频法原理 - CSDN 博客
https://blog.csdn.net/Cherish_x/article/details/76358436 -
FPGA 频率计实验_fpga 直接计数法 - CSDN 博客
https://blog.csdn.net/qq_39507748/article/details/109412196_ -
FPGA 频率测量的三种方法(直接测量法,间接测量法,等精度测量法)_fpga 测频率 - CSDN 博客
https://wuzhikai.blog.csdn.net/article/details/112326945